O documento apresenta técnicas de programação funcional em F# e Scala, como funções de alta ordem, imutabilidade, pattern matching e avaliação preguiçosa. Estas técnicas permitem maior confiabilidade no código e facilitam a manipulação de listas e estruturas de dados de forma funcional.

1. Em F# e Scala
Técnicas de Programação
Funcional
Vinícius Hana e Juliano Alves
@vinicius_hana e @vonjuliano

2. Apresentação

3. Primeiro de tudo: não são paradigmas
excludentes!

4. Programação funcional considera que
todas as operações são funções

5. Todas as operações são funções
def f(x: Int, g: (Int) => Int) = g(x) + 3
def g(x: Int) = x * 2
val resultado = f(4, g) // isso dá 11
5

6. Isso tem nome: funções de alta ordem

7. Perceberam que se parece com
matemática?

8. Todas as operações são funções
f(x) = x + 3
g(x) = x * 2
(f o g) = f(g(x)) = g(x) + 3
g(4) = 4 * 2 = 8  f(g(4)) = 8 +3 = 11
8

9. Funções de alta ordem permitem
algumas coisas bem legais!

10. Funções de alta ordem
let funcao =
let lista = [0;1;2;3;4]
List.map (fun x -> x * 2) lista
1
0

11. Agora, uma outra ideia:
Dado f(x) = x + 1, se eu passar sempre
1, sempre vai dar 2?

12. Sim!
E isso tem nome: transparência
referencial

13. Dada a mesma entrada, obteremos
sempre a mesma saída
Ou seja, ausência de efeitos colaterais

14. Dá pra fazer isso em programação?
Sim, usando imutabilidade!

15. Mutabilidade
public int Resultado { get; set; }
public void Dobrar(int numero)
{
Resultado *= 2;
}
1
5

16. Imutabilidade
DateTime.Now.AddDays(1);
// retorna novo datetime com a adição feita
1
6

17. Dada a mesma entrada, obteremos
sempre a mesma saída

18. Ou seja, ausência de efeitos colaterais
– mais confiabilidade no código

19. F# e Scala suportam mutabilidade e
imutabilidade

20. Imutabilidade em Scala e F#
let x = 1 // imutavel
let mutable x = 1 // mutavel
val x = 1 // imutavel
var y = 1 // mutavel
2
0

21. Isso ajuda demais em concorrência

22. Certo, mas como eu manipulo e altero
os itens de uma lista, então? Ela não é
imutável?

23. Simples: gere outra com nossa velha
amiga recursão!

24. Com recursão, podemos compor e
decompor listas

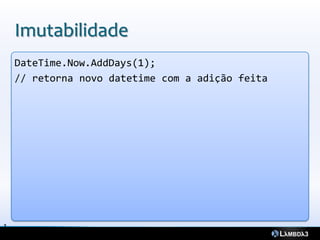
25. Recursão em listas
let rec reverse lista =
match lista with
| head :: tail -> (reverse tail) @ [head]
| [] -> []
def reverse[T](list: List[T]): List[T] = list match {
case head :: tail => reverse(tail) ++ List(head)
case Nil => Nil
}

26. Percebeu uma estrutura diferente
para compor a lista?

27. Essa estrutura se chama pattern
matching

28. Ela lembra switch-case, porém com
muito mais funcionalidade

29. Pattern matching
match coisa with
| 1 | 3 -> …
| head :: tail -> …
| [] -> …
| _ -> …
lista match {
case 1 => …
case head :: tail => …
case Nil => …
case _ => …
2
9

30. E se eu iterar em uma lista
gigantesca, ou mesmo infinita?

31. Lista infinita? Isso não arrebentaria
a memória?

32. Não se você tiver lazy evaluation!

33. Lazy evaluation
let x = 10
let resultado = lazy (x + 10)
val x = { println("x"); 1 }
lazy val y = { println("y"); 2 }
3
3

34. Vamos juntar tudo isso em uma
implementação de Fibonacci?

35. Fibonacci
let rec fib n =
match n with
| x when n > 2 -> 1
| _ -> fib (n - 1) + fib (n - 2)
val seq: Stream[BigInt] = 0 #:: 1 #:: (seq zip
seq.tail).map { case (a, b) => a + b }
def elemento(posicao: Int): BigInt = seq(posicao
- 1)
3
5

36. Referências

37. Obrigado!
Vinícius Hana e Juliano Alves
@vinicius_hana e @vonjuliano

38. www.lambda3.com.br