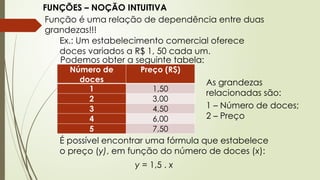
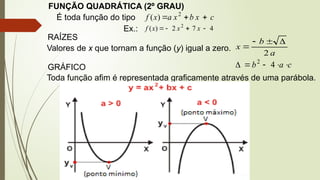
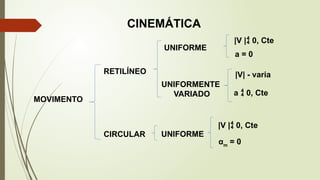
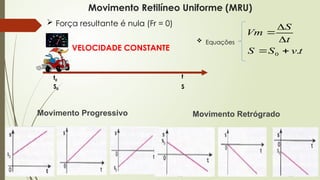
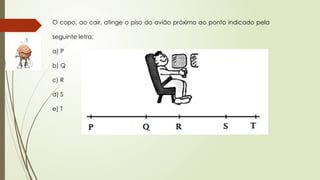
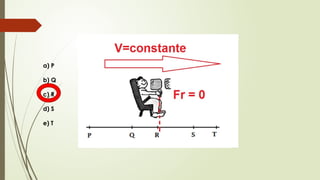
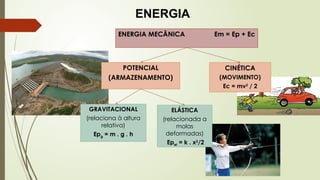
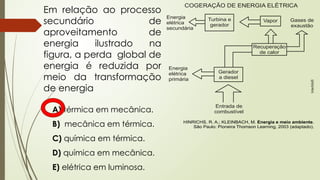
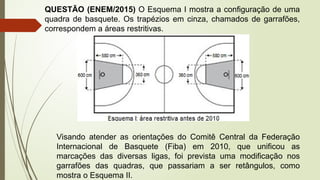
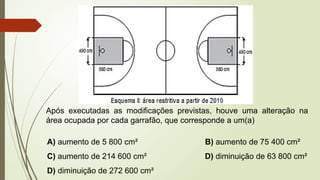
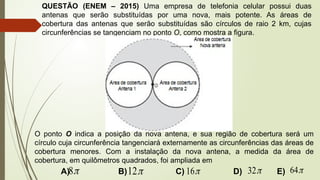
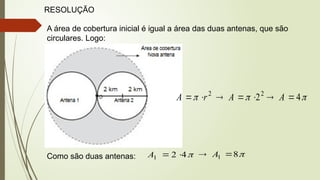
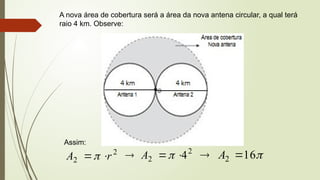
O documento aborda conceitos fundamentais de matemática e física, incluindo relações de dependência entre grandezas, funções lineares e quadráticas, probabilidade e cinemática. Ele utiliza exemplos práticos, como a pontuação em campeonatos e consumo familiar, para ilustrar a aplicação dessas funções. Além disso, analisa situações específicas como sorteios e condições climáticas que afetam eventos, buscando promover a interpretação e resolução de problemas.