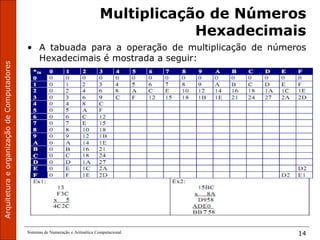
O documento aborda sistemas de numeração e aritmética computacional, enfatizando a importância do formato binário nas operações aritméticas em computadores. As operações de adição, subtração, multiplicação e divisão são discutidas em diferentes bases numéricas, incluindo binária, octal e hexadecimal. O texto também detalha os processos de 'vai 1' e 'empréstimo' nas operações, ilustrando a execução dessas operações com exemplos.