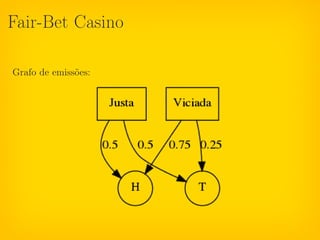
Este documento discute modelos ocultos de Markov (HMMs) e sua aplicação em problemas de biologia computacional. HMMs são modelos probabilísticos que podem ser usados para análise de séries e sequências. A biblioteca GHMM implementa HMMs em Python e é usada para resolver problemas como classificação, clusterização e reconhecimento de padrões em sequências biológicas.




















![GHMM
import ghmm
# Criando a l f a b e t o para r e p r e s e n t a r o s
# s i m b o l o s e m i t i d o s p e l o me modelo .
e m i s s i o n _ a l p h a b e t = ghmm. Alphabet ( [ ’H ’ , ’T ’ ] )](https://image.slidesharecdn.com/hmms-111107201956-phpapp01/85/Python-e-Cadeias-de-Markov-GHMM-22-320.jpg)
![GHMM
# Matriz de t r a n s i c o e s :
# l i n h a s r e p r e s e n t a m e s t a d o s de origem
# c o l u n a s r e p r e s e n t a m e s t a d o s de d e s t i n o
# v a l o r e s da m a t r i z r e p r e s e n t a m a
# p r o b a b i l i d a d e da t r a n s i c a o de e s t a d o s
#
transitions_probabilities = [
[ 0 . 9 , 0 . 1 ] , # 0 : e s t a d o de j u s t o
[ 0 . 1 , 0 . 9 ] , # 1: estado viciado
]](https://image.slidesharecdn.com/hmms-111107201956-phpapp01/85/Python-e-Cadeias-de-Markov-GHMM-23-320.jpg)
![GHMM
# p r o b a b i l i d a d e s de comecar em H e T
initial_states_distribution = [0.5 , 0.5]](https://image.slidesharecdn.com/hmms-111107201956-phpapp01/85/Python-e-Cadeias-de-Markov-GHMM-24-320.jpg)
![GHMM
# Matriz de e m i s s a o de s i m b o l o s
# 0 : p r o b a b i l i d a d e s de e m i s s a o da moeda j u s t a
emissions_fair = [0.5 , 0.5]
# 1 : p r o b a b i l i d a d e s de e m i s s a o da moeda v i c i a d a
emissions_biased = [ 0 . 5 , 0 . 5 ]
emissions_probabilities = [
emissions_fair ,
emissions_biased
]](https://image.slidesharecdn.com/hmms-111107201956-phpapp01/85/Python-e-Cadeias-de-Markov-GHMM-25-320.jpg)

![GHMM
Resolvendo o problema do Casino
t o s s e s = [ T, T, T, H, . . . , H, T ]
# XXX
s e q u e n c e = ghmm. Em i s s i o n S e q u e n c e ( e m i s s i o n _ a l p h a b e t ,
tosses )
v i t e r b i _ p a t h , s t a t e s _ p r o b = hmm. v i t e r b i ( s e q u e n c e )](https://image.slidesharecdn.com/hmms-111107201956-phpapp01/85/Python-e-Cadeias-de-Markov-GHMM-27-320.jpg)
![GHMM
Resolvendo o problema do Casino
>>> p r i n t ( v i t e r b i _ p a t h )
[0 , 0 , 0 , 0 , . . . , 1 , 1 , 1 , 1 , 1]
>>> p r i n t s t a t e s _ p r o b
[[0.8407944139086141 , 0.1592055860913865] ,
[0.860787703168127 , 0.13921229683187356] , . . . ]](https://image.slidesharecdn.com/hmms-111107201956-phpapp01/85/Python-e-Cadeias-de-Markov-GHMM-28-320.jpg)



