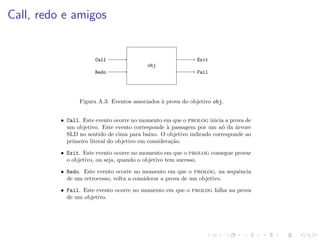
O documento apresenta o programa para o curso de Lógica para Programação em Prolog, cobrindo conceitos básicos, lógica proposicional e de primeira ordem usando sistemas dedutivos e de resolução, programação lógica e Prolog, e exemplos iniciais. Os tópicos incluem sintaxe de Prolog, unificação, comparação e expressões aritméticas de termos, listas, leitura e escrita de termos.

1. Lógica para Programação
LEIC-Tagus
P2
Prolog
Luı́sa Coheur
(slides fortemente baseados nos slides da Professora Inês Lynce)

2. Programa
• Conceitos Básicos (Livro: 1.1)
• Lógica Proposicional (ou Cálculo de Predicados) – sistema
dedutivo (2.1, 2.2.1, 2.2.2 e 2.2.4)
• Lógica Proposicional (ou Cálculo de Predicados) – resolução
(3.1)
• Lógica de Primeira Ordem – sistema dedutivo (4.1, 4.2)
• Lógica de Primeira Ordem – resolução (5.1 e 5.2)
• Programação em Lógica (6)
• Prolog (7 + Apêndice A: manual de sobrevivência em Prolog)
• Lógica Proposicional (ou de Predicados) – sistema semântico
(2.3, 2.4, 3.2)
• Lógica de Primeira Ordem – sistema semântico (4.3 e 4.4)

3. Paradigmas de programação
• Programação orientada a objectos (e.g. C++, Java)
• Programação funcional (e.g. Scheme, Lisp)
• Programação em lógica (e.g. Prolog)
• ...

4. PROLOG = PROgramação em LÓGica
• Introduzido nos anos 70 no âmbito do processamento de
linguagem natural (1972, Alain Colmerauer et al.)
– Colmerauer, A., Kanoui, H., Roussel, P . and Pasero, R. “Un
systeme de communication hommemachine en français”,
Groupe de Recherche en Intelligence Artificielle, Université
d’Aix-Marseille. 1973.

5. Programação em Lógica vs. Prolog
• Programa
– P(x, z) ← Q(x, y), P(y, z)
Prolog: p(X, Z) :- q(X, Y), p(Y, Z).
– P(x, x) ←
Prolog: p(X, X).
– Q(a, b) ←
Prolog: q(a, b).
• Objectivo
– ← P(x, b)
Prolog: ?- p(X, b).
• Função de selecção do Prolog (o primeiro literal do objectivo):
S1(← α1, . . . , αn) = α1
• Regra de procura do Prolog: começa a procurar cláusulas para
unificar de cima para baixo

6. Programação em lógica: programa responde a perguntas

7. Exemplos Iniciais (7.6): programa (factos e regras)
f(a).
f(b).
g(b).
g(c).
r(X) :- f(X), g(X).
r(d).

8. Exemplo: objectivo (questão)
?- r(X).

9. Nota sobre o Prolog:
• O Prolog segue estratégia de procura em profundidade com
retrocesso
– Pode nunca encontrar solução (mesmo que ela exista) caso
siga por um caminho infinito

10. Unificação de termos (7.2)
• Predicado de unificação: =
– ht1i = ht2i tem sucesso se os termos ht1i e ht2i podem ser
unificados; se sim são feitas as substituições
• Negação do predicado de unificação: =
– ht1i = ht2i tem sucesso se ht1i e ht2i não podem ser
unificados

11. Unificação de termos: exemplos
?- a = b.
?- f(X, a) = f(b, Y).
?- X = a.
?- X = X.
?- X = Y.
?- f(X, a) = f(b, X).
?- xpto(rui, ana) = xpto(X, Y).
?- f( , X, ) = f(a, b, c).

12. Unificação de termos: exemplos
?- a = b.
false
?- f(X, a) = f(b, Y).
X = b, Y = a
?- X = a.
X = a
?- X = X.
true
?- X = Y.
X = Y
?- f(X, a) = f(b, X).
false
?- xpto(rui, ana) = xpto(X, Y).
X = rui, Y = ana
?- f( , X, ) = f(a, b, c).
X = b

13. Sobre as variáveis em Prolog
• Uma vez unificadas, é uma relação para sempre!
• ?- X = a, X = b.
false

14. Comparação de termos (7.3)
• Operadores de comparação: == e == testam se dois
termos são iguais (diferentes) não instanciando variáveis (e
não avalia numericamente)
• Exemplos:
?- 4 == 1 + 3.
?- a == a.
?- a == ‘a’.
?- a == b.
?- X == Y.
?- X == a.
?- X = a, X == a.
?- X == a, X = a.
?- X = a, Y = a, X == Y.

15. Comparação de termos: exemplos
?- 4 == 1 + 3.
false
?- a == a.
true
?- a == ‘a’.
true
?- a == b.
false
?- X == Y.
false
?- X == a.
false
?- X = a, X == a.
X = a
?- X == a, X = a.
false
?- X = a, Y = a, X == Y.
X = a, Y = a

16. Expressões aritméticas (7.7)
• Igualdade aritmética: =:=
– hn1i =:= hn2i tem sucesso se hn1i e hn2i são o mesmo número
(avalia numericamente);
• Negação do predicado da igualdade aritmética: = =
– hn1i = = hn2i tem sucesso se hn1i e hn2i não são o mesmo
número;

17. Comparação de termos: exemplos
?- X = 4, X == 3 + 1.
false.
?- X = 4, X =:= 3 + 1.
X = 4.
?- X = 4, 3 + 1 =:= X.
X = 4.

18. Expressões aritméticas: predicado pré-definido “is”
• = unifica mas não faz avaliação numérica
– Por exemplo
?- A = 1+2, A == 3.
false
• is avalia numericamente a expressão do lado direito e unifica
com a do lado esquerdo
– Por exemplo
?- A is 1+2, A == 3.
A = 3

19. Expressões aritméticas: exemplo
• Com utilização de , para a conjunção e ; para disjunção
?- X is 3+4.
X = 7
?- (6>5, 3 =:= 4, X is 3; X is 8).
X = 8
?- (6>5, 3 == 4, X is 3; X is 8).
X = 3

20. Expressões aritméticas e unificação: mais exemplos
?- 2 + 3 = +(2, 3).
?- 2 + 3 = +(3, 2).
?- X = +(2, 3).
?- 2 + X = Y + 3.
?- 5 < 7.
?- 3 + 5 > 12.
?- 3 + 5 >= +(4, +(2, 2)).
?- X > 12.

21. Expressões aritméticas e unificação: mais exemplos
?- 2 + 3 = +(2, 3).
true.
?- 2 + 3 = +(3, 2).
false.
?- X = +(2, 3).
X = 2+3.
?- 2 + X = Y + 3.
X = 3,
Y = 2.
?- 5 < 7.
true.
?- 3 + 5 > 12.
false.
?- 3 + 5 >= +(4, +(2, 2)).
true.
?- X > 12.
ERROR: >/2: Arguments are not sufficiently
instantiated

22. Polimodalidade
• Capacidade de utilizar múltiplos modos de interacção com um
programa (diferentes argumentos instanciados).
soma 5 e duplica(X, Y) :- Y is 2 * (X + 5).
?- soma 5 e duplica(10, Y).
?- soma 5 e duplica(10, 30).
?- soma 5 e duplica(X, 30).

23. Exemplo: polimodalidade
soma 5 e duplica(X, Y) :- Y is 2 * (X + 5).
?- soma 5 e duplica(10, Y).
Y = 30.
?- soma 5 e duplica(10, 30).
true.
?- soma 5 e duplica(X, 30).
ERROR: is/2: Arguments are not sufficiently
instantiated

24. Momento de Aprendizagem Activa

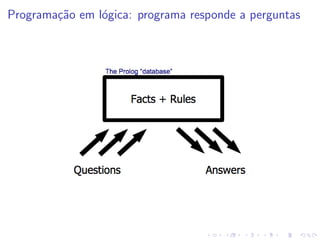
25. Listas (as vossas melhores amigas nos próximos tempos):
(7.10)
• Lista = sequência de elementos limitados por parêntesis rectos
(ex: [1, . . . , −5], [ola, 2, ola(2, 4), X])
• [ ] representa a lista vazia
• O sı́mbolo | permite referir o(s) elementos à cabeça e na
cauda da lista (que é uma lista) (ex: [ Cabeca | Cauda ])

26. Exemplo: a lista [ca, hf, vn] unifica com
• [Cabeca | Cauda] % Cabeca = ca, Cauda = [hf, vn]
• [ca | Cauda] % Cauda = [hf, vn]
• [El1, El2 | Cauda] % El1 = ca, El2 = hf, Cauda = [vn]
• [ca, hf | Cauda] % Cauda = [vn]
• [ca, hf, vn |[]]
• ...

27. Exemplo: último de uma lista (o primeiro conseguimos
sempre obter com o |)
• ultimo([X], X).
• ultimo([ | Cauda], X) :- ultimo(Cauda, X).

28. Exemplos maravilha – código na página
• somaRec(Lista, N, Soma).
• somaIt(Lista, N, Soma).
• maiorRec(Lista, N, NovaLista).
• maiorIt(Lista, N, NovaLista).

29. Mas então podemos ter predicados com o mesmo nome e
um número diferente de argumentos (pergunta relativa à
versão Iterativa)?

30. Overloading de predicados em Prolog
• Sim, é possı́vel fazer overloading de predicados
– O mesmo predicado pode ter um número de argumentos
diferente

31. Instruções de Leitura (7.8)
?- read(X).
|: a.
X = a.
?- read(b).
|: a.
false.
?- X = b, read(X).
|: a.
false.
?- read(X).
|: 3 + 2.
X = 3+2.
? - read(X).
|: 3 mais 2.
ERROR: Stream user input:0:113 Syntax error:
Operator expected

32. Instruções de Escrita
?- write(a), write(b).
ab
true.
?- writeln(a), write(b).
a
b
true.
?- write(+(2,3)).
2+3
true.

33. RESUMO
• A partir daqui temos um resumo do que foi dado nas aulas,
complementado com mais detalhes e exemplos

34. Componentes básicos (7.1)
• Termos
– Constantes
– Variáveis
– Termos compostos
• Literais
• Programa: conjunto de cláusulas determinadas
– Afirmações
– Regras
• Objectivos

35. Constantes
• Constantes: átomos + números
• Átomos
– Cadeias de caracteres que podem incluir letras, dı́gitos e
(underscore) e que têm de ser iniciadas por letra minúscula
I ana, nuno, ana silva, x 25
– Cadeias de caracteres limitadas por plicas
I ’ana’, ’Ana Silva’
– Átomos especiais
I []{}!; . . .
• Números
– Inteiros e reais
I 1, -97, 3.1415, -0.0035

36. Variáveis
• Cadeias de caracteres que podem incluir letras, dı́gitos e e
que têm de ser iniciadas por letra Maiúscula ou
– X, Resultado, Lista participantes, x23
• Variável representa uma variável sem nome
• O domı́nio de uma variável corresponde a uma única cláusula
• Atenção: chamam-se variáveis singleton às que aparecem uma
única vez numa cláusula; devem ser substituı́das por

37. Termos compostos
• Permitem criar objectos que agrupam um conjunto de
objectos:
– tipo-de-objecto(componente-1, componente-2, . . .)
• Exemplos
– data(Dia, Mes, Ano).
I data(14, novembro, 2007).
I data(25, dezembro, 2000).
– dataDeNasc(fern pessoa, data(13, junho, 1888)).

38. Literais
• Correspondem à aplicação de um predicado ao número
apropriado de termos
– Não existe diferença sintáctica entre literal e termo composto
• Exemplos
– ad(rui, X)
– ant(rui, ana)
– urso(winnie)

39. Programa: factos + regras
• Factos
– correspondem a afirmações;
– correspondem a cláusulas de Horn com um literal positivo;
– consistem em letras de predicado (iniciados com minúscula)
com 1 ou + argumentos e terminados com um ponto final.
– Exemplos
I mulher(ana).
I frequenta(rui, lp).

40. Programa: factos + regras
• Regras
– permitem realizar inferência;
– correspondem a cláusulas de Horn com um literal positivo e
pelo menos um literal negativo;
– são usados os sı́mbolos “:-”, “,”, “;” e terminam com um
ponto final. A interpretação destes sı́mbolos é a seguinte:
I O operador “:-” deve ser interpretado como “se”;
I O “,” deve ser interpretada como “e” (e o “;” como “ou”).
• Exemplo
– % X é avô de Z se X for ascendente directo de Y e Y for
ascendente directo de Z
– avo(X,Z) :- ascendente directo(X,Y),
ascendente directo(Y,Z).

41. Programa: executar um programa
• Executar um programa implica colocar questões
(correspondem a objectivos);
• Objectivos são cláusulas de Horn que têm somente literais
negativos.
– Exemplo
I :- avo(pedro,nuno).
I Na janela de interacção ?- avo(pedro,nuno).

42. Exemplo básico de interacção em Prolog
• Janela de interacção
– Linux: comando pl
– Mac: comando swipl
– Windows: comando plwin.exe
I Tipicamente é criado um shortcut no Desktop durante a
instalação
I No caso de se pretender trabalhar na linha de comandos
(MS-DOS) usar plcon.exe
– Aceita somente comandos e objectivos
– Termina com o comando halt. (ou CTRL+D)

43. Exemplo básico de interacção em Prolog (cont.)
• Programa (regras ou factos) + Objectivo
– Unificação é fundamental
• Tipicamente programas são escritos num ficheiro (.pl)
– ?- [<nome-programa>]. /*carrega o programa*/
• Objectivos também podem ser incluı́dos no ficheiro
– Antecedidos por :-
• Objectivos com várias respostas
– <Enter> aceita uma resposta
– ; pede a resposta seguinte

44. Exemplo básico de interacção em Prolog

45. Semântica do Prolog (7.5)
• Semântica declarativa: aquilo que um programa afirma.
Assim, a(X) :- b(X), c(X). pode ser lida como “se b(X) e
se c(X) se verificam para uma dada substituição para a
variável X, então podemos concluir que a(X) também se
verifica para essa substituição”.
• Semântica procedimental: como provar um objectivo com um
determinado programa. O exemplo anterior pode ser lido
como “para provar a(X) temos de provar uma instância de
b(X) e depois c(X), com as substituições adequadas de X”.

46. Semântica (procedimental) do Prolog
• Programa: sequência de cláusulas determinadas
• Execução (prova) de um objectivo: refutação SLD cuja função
de selecção devolve o primeiro literal e a regra de procura
escolhe a primeira cláusula unificável

47. Exemplo: programa
ad(pedro, ana).
ad(rui, pedro).
ant(X, Y) :- ad(X, Y).
ant(X, Z) :- ad(Y, Z), ant(X, Y).

48. Exemplo: objectivos
?- ant(rui, ana).
?- ant(rui, X).
?- ant(X, ana).
?- ant(X, Y).
?- ant(rui, ).
?- ant( , ana).
?- ant(eva, ana).

49. Exemplo: resultados

50. Exemplo: questão
• E se em vez de:
ant(X, Z) :- ad(Y, Z), ant(X, Y).
estivesse:
ant(X, Z) :- ant(X, Y), ad(Y, Z).?

51. Exemplo: oops

52. Exemplo: programa + objectivos
inteiro(0).
inteiro(s(X)) :- inteiro(X).
?- inteiro(0).
?- inteiro(s(0)).
?- inteiro(X).

53. Exemplo: resultados (pedindo mais soluções ou não)

54. Exemplo: factorial
factorial(1,1).
factorial(N,F) :- N > 1,
N menos 1 is N-1,
factorial(N menos 1, F N menos 1),
F is N * F N menos 1.

55. Exemplo: factorial - sequência de objectivos
factorial(3,X)
factorial(2, F N menos 11)
factorial(1, F N menos 12)
?- factorial(X,6) % erro: falha na polimodalidade

56. Exemplo: factorial (versão 2)
factorial(N,F) :- N > 1,
N menos 1 is N-1,
factorial(N menos 1, F N menos 1),
F is N * F N menos 1.
factorial(N, F) :- fact(N, 1, F).
fact(1, F, F).
fact(N, Ac, F) :- N > 1,
Ac act is N * Ac,
N act is N - 1,
fact(N act, Ac act, F).

57. Exemplo: factorial (versão 2) - sequência de objectivos
factorial(3,X)
factorial(3,1,X)
factorial(2,3,X)
factorial(1,6,X)

58. Call, redo e amigos
SOBREVIVÊNCIA EM PROLOG 373
obj
Redo
Call
Fail
Exit
Figura A.3: Eventos associados à prova do objetivo obj.
• Call. Este evento ocorre no momento em que o prolog inicia a prova de
um objetivo. Este evento corresponde à passagem por um nó da árvore
SLD no sentido de cima para baixo. O objetivo indicado corresponde ao
primeiro literal do objetivo em consideração.
• Exit. Este evento ocorre no momento em que o prolog consegue provar
o objetivo, ou seja, quando o objetivo tem sucesso.
• Redo. Este evento ocorre no momento em que o prolog, na sequência
de um retrocesso, volta a considerar a prova de um objetivo.
• Fail. Este evento ocorre no momento em que o prolog falha na prova
de um objetivo.
O meta-predicado de sistema trace/1, aceita como argumento o nome de um
outro predicado e permite seguir o rasto da avaliação do predicado especificado.
Exemplo A.7.1 Consideremos o programa do Exemplo 7.6.1: