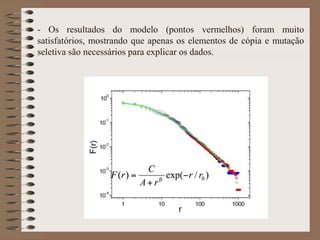
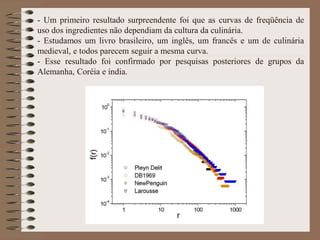
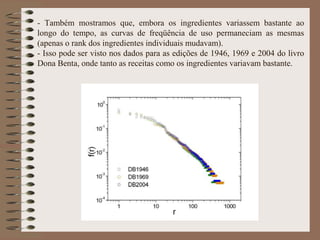
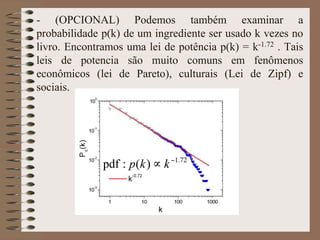
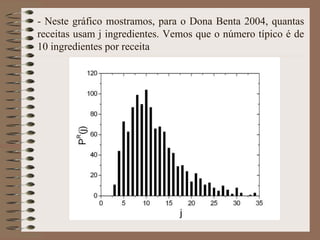
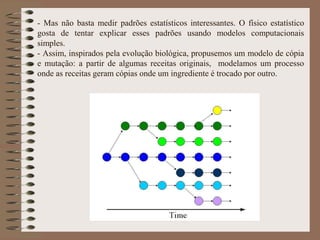
O documento apresenta uma pesquisa pioneira sobre a aplicação da Física Estatística na culinária, chamada de Gastronofísica. Estudou padrões estatísticos em redes de receitas e ingredientes em livros de culinária de diferentes culturas, e propôs um modelo de cópia e mutação que explicou os dados observados.

1. Gastronofísica: Física Estatística aplicada
à culinária
- Olá, meu nome é Osame Kinouchi e sou docente no departamento de
Física da Faculdade de Filosofia, Ciências e Letras de Ribeirão Preto.
- Coordeno o Laboratório FEBiC - Física Estatística e Biologia
Computacional. Em alguns instantes explicarei melhor o que a Física
Estatística trata.
- Nossas principais linhas de pesquisa se referem a aplicações da Física
Estatística na modelagem de vários sistemas biológicos (redes
neuronais, processos de colonização, enxames de mosquitos, evolução
biológica etc.). Também estudamos redes sociais complexas, por
exemplo, as que podem ser extraídas a partir de biografias.

2. O que é Física Estatística?
» A Física Estatística é a parte da física que estuda sistemas
com muitas unidades interagentes, tais como átomos,
moléculas, spins magnéticos etc.
» Seu principal interesse é estudar as fases da matéria (sólida,
líquida, gasosa, fase magnética etc.)
» Mas logo se percebeu que as ideias e técnicas desenvolvidas
pela física estatística poderiam ter aplicações
interdisciplinares, por exemplo:
» Sistemas de muitos agentes econômicos, que são estudados
pela Econofísica
» Sistemas de muitos agentes sociais, que são estudados pela
Sociofísica
» Sistemas de muitos neurônios interagindo
» Sistemas de muitas espécies biológicas interagindo
» Sistemas de muitos animais interagindo em enxames,
bandos de pássaros ou cardumes
» Etc. etc. etc.

3. - Nesta aula eu vou apresentar um trabalho em um assunto bastante
inusitado: a aplicação de Física Estatística na culinária, o que
poderíamos chamar de Gastronofísica.
- É um trabalho de nosso grupo que chamou bastante atenção por ter
sido pioneiro, publicado em 2008. Outros trabalhos no mesmo assunto
se seguiram, por vários grupos internacionais.
• Mas por que Culinária?
• Bom, tudo começou com um jantar na casa de
Antonio Carlos Roque, meu colega físico, e
sua esposa Rosa Diez-Garcia, professora de
nutrição na Faculdade de Medicina de
Ribeirão Preto.
• Estávamos discutindo ideias sobre redes
complexas e Rosa perguntou se seria possível
aplicar essas ideias na culinária, por exemplo
na rede formada por receitas e ingredientes.
• Concordamos que valia a pena investigar se
tais redes apresentariam padrões estatísticos
interessantes.

4. - Eis a forma de uma rede de receitas e ingredientes. Um dado importante é
o número de links de cada ingrediente (quantas vezes o ingrediente foi
usado no livro, ou seja, quantas receitas usaram aquele ingrediente)
Receitas
Ingredientes

5. • Embora já naquela época existissem bancos de dados enormes de
receitas na internet, achamos melhor começar com os livros
tradicionais de receita, como o Dona Benta e o Larrouse
Gastronomique.
• Coletamos estatísticas tais como a quantidade de ingredientes por
receita e quantas receitas usavam cada ingrediente. Isso nos permitiu
construir curvas da freqüência f(r) com que cada ingrediente foi
usado, onde r é o rank (popularidade) do ingrediente.

6. - Um primeiro resultado surpreendente foi que as curvas de freqüência de
uso dos ingredientes não dependiam da cultura da culinária.
- Estudamos um livro brasileiro, um inglês, um francês e um de culinária
medieval, e todos parecem seguir a mesma curva.
- Esse resultado foi confirmado por pesquisas posteriores de grupos da
Alemanha, Coréia e índia.

7. - Também mostramos que, embora os ingredientes variassem bastante ao
longo do tempo, as curvas de freqüência de uso permaneciam as mesmas
(apenas o rank dos ingredientes individuais mudavam).
- Isso pode ser visto nos dados para as edições de 1946, 1969 e 2004 do livro
Dona Benta, onde tanto as receitas como os ingredientes variavam bastante.

8. - (OPCIONAL) Podemos também examinar a
probabilidade p(k) de um ingrediente ser usado k vezes no
livro. Encontramos uma lei de potência p(k) = k-1.72 . Tais
leis de potencia são muito comuns em fenômenos
econômicos (lei de Pareto), culturais (Lei de Zipf) e
sociais.

9. - Neste gráfico mostramos, para o Dona Benta 2004, quantas
receitas usam j ingredientes. Vemos que o número típico é de
10 ingredientes por receita

10. - Mas não basta medir padrões estatísticos interessantes. O físico estatístico
gosta de tentar explicar esses padrões usando modelos computacionais
simples.
- Assim, inspirados pela evolução biológica, propusemos um modelo de cópia
e mutação: a partir de algumas receitas originais, modelamos um processo
onde as receitas geram cópias onde um ingrediente é trocado por outro.

11. - No nosso modelo cada ingrediente i possui um número fi (fitness) que mediria
seu custo, disponibilidade, sabor etc.
- O ingrediente é substituido se o novo ingrediente sorteado tiver fitness maior
fi
fj
Substituo se fj > fi
Fitness fi intervalo [0,1]
Conjunto total de ingredientes
Receita com K ingredientes

12. - Os resultados do modelo (pontos vermelhos) foram muito
satisfatórios, mostrando que apenas os elementos de cópia e mutação
seletiva são necessários para explicar os dados.

13. - Obtivemos outro resultado que não esperávamos: mesmo com a
constante substituição de ingredientes com maior fitnesses, no final
do processo sempre sobravam ingredientes com baixo fitness.

14. - Em biologia, esse fenômeno é conhecido como Efeito do Fundador: genes que estavam
em uma população pequena fundadora (por exemplo, um bando de pássaros que coloniza
uma ilha) permanecem na população, mesmo que não tenham bom fitness.
- No nosso caso, alguns ingredientes presentes no conjunto inicial de receitas permanem
na culinária, não importa seu fitness. Interpretamos isso como ingredientes tradicionais e
idiossincráticos da culinária, que não são substituídos por ingredientes estrangeiros.

15. Encerramento
• Hoje em dia, a Física Estatística
tem inúmeras aplicações
interdisciplinares
• Neste trabalho pioneiro,
publicado em 2008, mostramos
que se pode estudar e modelar a
rede de receitas-ingredientes com
as técnicas da Física Estatística
• Em particular, a frequência de uso
dos ingredientes pode ser
modelada por um processo de
cópia e mutação Darwiniano
• Sem ter sido planejado para isso,
o modelo evolutivo também
apresentou o Efeito do Fundador