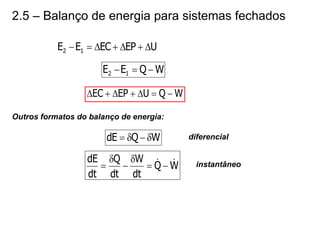
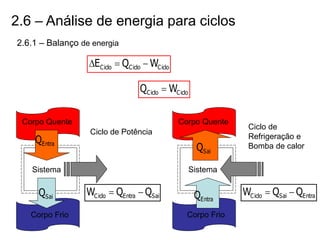
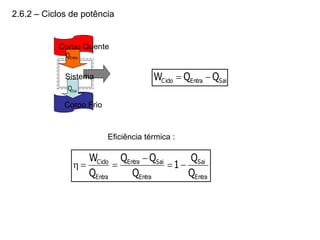
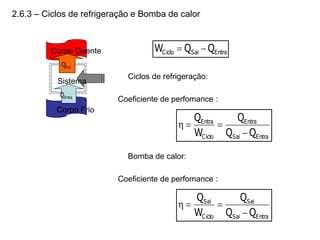
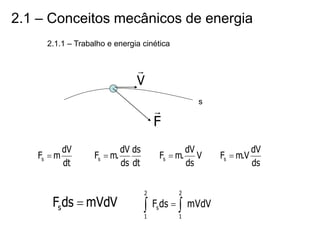
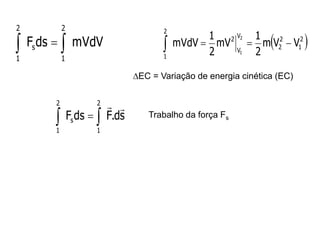
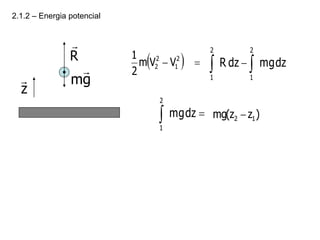
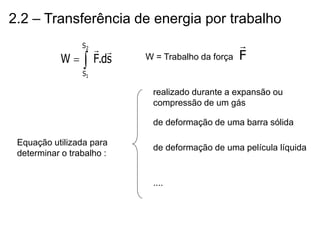
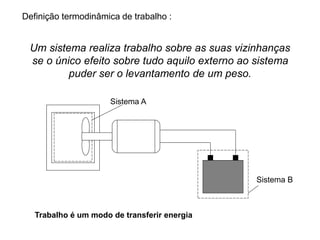
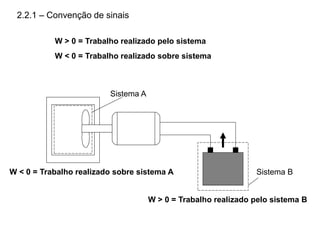
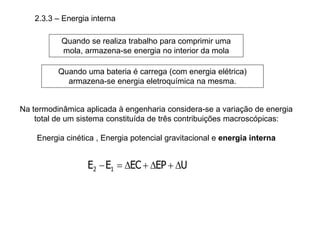
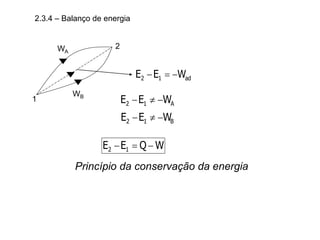
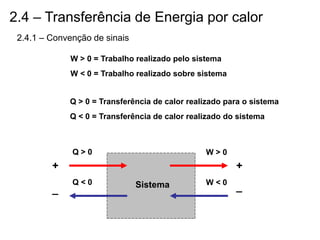
O capítulo descreve conceitos de energia mecânica e termodinâmica. Apresenta as definições de trabalho, energia cinética e potencial. Estabelece a primeira lei da termodinâmica, que relaciona a variação de energia de um sistema à quantidade de trabalho e calor transferidos. Por fim, discute análise energética para processos cíclicos.

1. Cap. 2 – Energia e Primeira Lei da
Termodinâmica

2. 2.1 – Conceitos mecânicos de energia
V

2.1.1 – Trabalho e energia cinética
s
F

dt
dV
m
Fs 
dt
ds
ds
dV
.
m
Fs  V
ds
dV
.
m
Fs 
ds
dV
V
.
m
Fs 
mVdV
ds
Fs  mVdV
ds
F
2
1
s
2
1

 

3. mVdV
ds
F
2
1
s
2
1

   
2
1
2
2
V
V
2
2
1
V
V
m
2
1
V
m
2
1
mVdV
2
1




EC = Variação de energia cinética (EC)
Trabalho da força Fs
s
d
.
F
ds
F
2
1
s
2
1



 

4. 2.1.2 – Energia potencial
R

g
m

z

  
 2
1
2
2 V
V
m
2
1
dz
mg
dz
R
2
1
2
1

 
)
z
z
(
mg 1
2 

 dz
mg
2
1

5. 2.2 – Transferência de energia por trabalho
W = Trabalho da força
s
d
.
F
W
2
1
S
S



 F

Equação utilizada para
determinar o trabalho :
realizado durante a expansão ou
compressão de um gás
de deformação de uma barra sólida
de deformação de uma película líquida
....

6. Definição termodinâmica de trabalho :
Um sistema realiza trabalho sobre as suas vizinhanças
se o único efeito sobre tudo aquilo externo ao sistema
puder ser o levantamento de um peso.
Sistema A
Sistema B
Trabalho é um modo de transferir energia

7. 2.2.1 – Convenção de sinais
W > 0 = Trabalho realizado pelo sistema
W < 0 = Trabalho realizado sobre sistema
Sistema A
Sistema B
W > 0 = Trabalho realizado pelo sistema B
W < 0 = Trabalho realizado sobre sistema A

8. s
d
.
F
W
2
1
S
S




Trabalho não é uma propriedade do sistema !
1
2 W
W
W 



2
1
W
W Diferencial inexata
Potência:
dt
W
dt
V
.
F
dt
dt
s
d
.
F
W
2
1
2
1
2
1
t
t
t
t
S
S







 


dt
W
W


 Diferencial inexata

9. 2.2.2 – Trabalho de expansão ou compressão
gás
gás
F=pA
dx
A
p
W 
 Diferencial inexata
dx
dV
p
W 



2
1
dV
p
W

10. 

2
1
dV
p
W
p
V
p
V
Um processo (em quase-equilíbrio)
descrito pela expressão pVn = cte é
chamado de um
processo politrópico

11. 2.2.3 – Exemplos de trabalho
a) Alongamento de uma barra sólida
dx
A
s
d
.
F
W
2
1
2
1
S
S
S
S



 



b) Potência transmitida por um eixo








 

 R
R
V
.
F
W



c) Potência eletrica
d) Trabalho devido a magnetização

12. 2.3 – Energia de um sistema
2.3.1 – Primeira Lei da Termodinâmica
O trabalho líquido realizado por ou sobre um sistema fechado
submetido a um processo adiabático entre dois estados dados,
dependo somente dos estados inicial e final.
2.3.2 – Variação de energia
ad
1
2 W
E
E 

 (ad = processo adiabático)
E = energia total - propriedade
Energia total inclui : Energia cinética , Energia potencia e outras formas

13. 2.3.3 – Energia interna
Quando se realiza trabalho para comprimir uma
mola, armazena-se energia no interior da mola
Quando uma bateria é carrega (com energia elétrica)
armazena-se energia eletroquímica na mesma.
Na termodinâmica aplicada à engenharia considera-se a variação de energia
total de um sistema constituída de três contribuições macroscópicas:
Energia cinética , Energia potencial gravitacional e energia interna
U
EP
EC
E
E 1
2 







14. 2.3.4 – Balanço de energia
1
2
ad
1
2 W
E
E 


WA
WB
A
1
2 W
E
E 


B
1
2 W
E
E 


W
Q
E
E 1
2 


Princípio da conservação da energia

15. 2.4 – Transferência de Energia por calor
2.4.1 – Convenção de sinais
W > 0 = Trabalho realizado pelo sistema
W < 0 = Trabalho realizado sobre sistema
Q > 0 = Transferência de calor realizado para o sistema
Q < 0 = Transferência de calor realizado do sistema
Q > 0 W > 0
+
+
Q < 0 W < 0
_ _
Sistema

16. 

2
1
Q
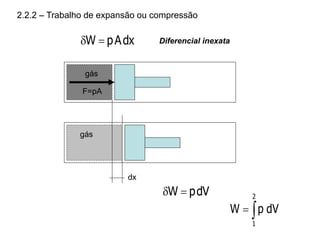
Q Diferencial inexata
Transferência de calor não é uma propriedade do sistema !
Taxa de transferência de calor:
dt
Q
Q
2
1
t
t



dt
Q
Q



(Potência térmica) [J/s] ou [W]


A
dA
q
Q 
 q
 = fluxo de calor [W/m2]

17. 2.5 – Balanço de energia para sistemas fechados
U
EP
EC
E
E 1
2 






W
Q
E
E 1
2 


W
Q
U
EP
EC 






Outros formatos do balanço de energia:
W
Q
dE 


 diferencial
W
Q
dt
W
dt
Q
dt
dE 
 




 instantâneo

18. 2.6 – Análise de energia para ciclos
2.6.1 – Balanço de energia
Ciclo
Ciclo
Ciclo W
Q
E 


Ciclo
Ciclo W
Q 
Corpo Quente
Corpo Frio
Sai
Q
Entra
Q
Sai
Entra
Ciclo Q
Q
W 

Sistema
Ciclo de Potência
Corpo Quente
Corpo Frio
Sai
Q
Entra
Q Entra
Sai
Ciclo Q
Q
W 

Sistema
Ciclo de
Refrigeração e
Bomba de calor

19. 2.6.2 – Ciclos de potência
Sai
Entra
Ciclo Q
Q
W 

Corpo Quente
Corpo Frio
Sai
Q
Entra
Q
Sistema
Entra
Sai
Entra
Sai
Entra
Entra
Ciclo
Q
Q
1
Q
Q
Q
Q
W






Eficiência térmica :

20. 2.6.3 – Ciclos de refrigeração e Bomba de calor
Entra
Sai
Ciclo Q
Q
W 

Corpo Quente
Corpo Frio
Sai
Q
Entra
Q
Sistema
Entra
Sai
Entra
Ciclo
Entra
Q
Q
Q
W
Q




Coeficiente de perfomance :
Ciclos de refrigeração:
Entra
Sai
Sai
Ciclo
Sai
Q
Q
Q
W
Q




Coeficiente de perfomance :
Bomba de calor:

21. Segunda lista de exercícios
2.17 – 2.28 – 2.31 – 2.47 – 2.48 – 2.53 – 2.61 – 2.63