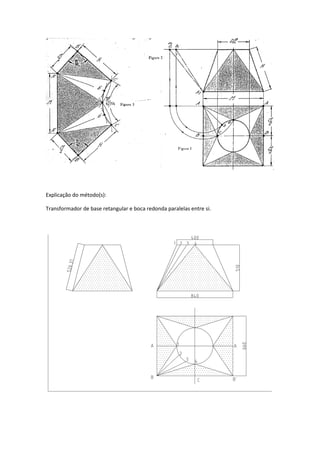
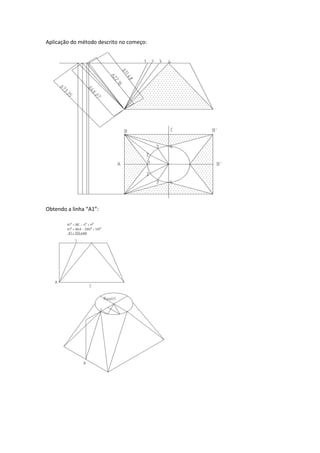
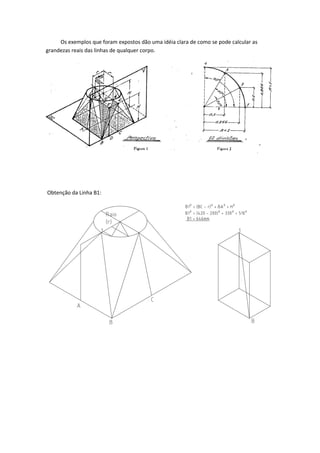
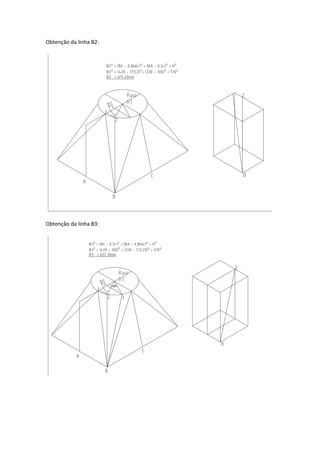
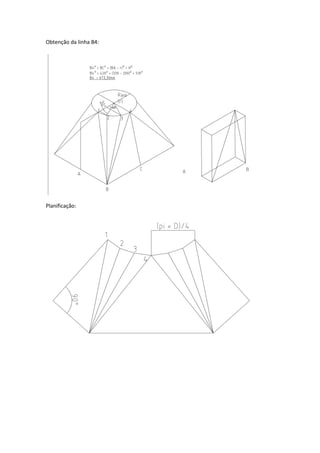
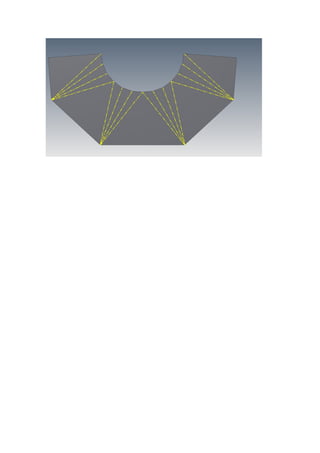
Este documento descreve o método para modelar um transformador de base quadrada e boca circular através da obtenção das linhas geratrizes. Primeiro, o quadrante interno da circunferência é dividido em partes iguais e os pontos são unidos ao ponto central A por meio de retas geratrizes. Estas geratrizes determinam novos pontos na extensão superior, formando as linhas reais do transformador. O desenvolvimento é feito marcando pontos ao longo das geratrizes e flexionando uma régua sobre estes pontos.

1. Transformador de boca circular e de base quadrada e paralela
Este transformador compõe-se de quatro segmentos de cones oblíquos iguais e de qua-
tro superfícies triangulares também iguais. Nas projeções horizontal e vertical(fig1 e 2) o
transformador foi representado por sua fibra interna.
Como os quatros segmentos de cones são iguais só determinaremos os dados de um de-
les. Portanto, dividiremos o quadrante interno de circunferência(fig1) em um número de
partes iguais(dois, por exemplo), unindo depois os pontos de divisão a, b e c com o ponto A
por meio de retas geratrizes. Estas geratrizes são giradas em redor do ponto A, determinando
novos pontos sobre o prolongamento do lado A-A. A partir dests pontos traçam-se perpend-
iculares, ao prolongamento da boca superior(fig2) cortando-a nos pontos a1, b1 e c1. (O ponto
a1 e c1 – neste caso – é o mesmo, já que as geratrizes Aa e Ac são iguais).
Os pontos a1, b1 e c1 são unidos com o ponto A1, ficando assim determinadas as
geratrizes reais que precisamos para desenvolver o transformador.
Desenvolvimento(fig3). Em uma posição adequada traça-se a reta A’-A’ de comprimento
igual ao comprimento interno M do lado da base do transformador(fig1) e, marcando o centro
nos pontos A1, descrevem-se arcos de raios iguais à geratriz real A1a1 da figura2, determi-
nando pela intersecção de ambos o ponto a’. Depois descrevem-se arcos desde os pontos A’ e
em ambas as partes de a’ com raios iguais às geratrizes reais A1b1 e A1c1, determinando assim
a posição dos pontos da curva da boca.
Em seguida, transporta-se sobre uma régua flexível meio desenvolvimento da circunfe-
rência média da boca (pi * Dmédio)/2 dividindo-se em quatro partes – (pi * D)/4 – iguais neste
caso. Esses pontos de divisão são chamados a, b e c e colocaremos o ponto a da régua sobre o
ponto a’ do desenvolvimento, flexionando a régua até que os pontos b e c da mesma coinci-
dam com os arcos da mesma origem, determinando os pontos b’ e c’ que se unem com os pon-
tos A’, marcando ao mesmo tempo a curva deixada pela régua flexível.
Marcando o centro no ponto c’(em ambas as partes) descreve-se um arco de raio H, to-
mado da figura2, e traçando outro arco desde o ponto A’ de raio igual à metade do lado
interno da base (M/2) determinaremos, por intersecção com o outro arco, ponto B’ que se une
com os pontos A’ e c’, ficando assim desenvolvido meio transformador.(As superfícies planas
são sombreadas).

2. Explicação do método(s):
Transformador de base retangular e boca redonda paralelas entre si.

3. Aplicação do método descrito no começo:
Obtendo a linha “A1”:

4. Método de cálculo(incluso a obtenção da linha “A1”, vista anteriormente):
A perspectiva da figura 1 representa um transformador de base quadrada e boca
superior central circular, estando a base apoiada no plano H de projeção, com um dos lados
tocando o plano V de projeção.
Um quadrante da boca circular foi dividido, neste caso, em três partes iguais, limitadas
pelos pontos 1, 2, 3 e 4.
A título de exemplo para calcular a grandeza real de qualquer linha traçada sobre a
superfície do transformador(neste caso as linhas B2 e B4) forma projetados os pontos de
divisão 2 e 4, perpendicularmente sobre o plano V de projeção, que é cortado nos pontos 2’ e
4’, respectivamente.
Esses pontos foram unidos com o ponto B da base, formando-se assim os respectivos
triângulos retângulos 2B2’ e 4B4’.
O valor da ordenada 4 é igual ao raio r e o valor da ordenada 2 é igual a 0,5*r. O valor da
abscissa 2 é igual a 0,866*r.
Valores constantes das ordenadas e abscissas. Os valores constantes de qualquer orde-
nada de uma circuferência de raio1 são iguais ao seno do ângulo formado pela linha central da
circunferência e pela reta que une o centro desta circuferência com o ponto de coordenadas
como, por exemplos, o ângulo de 30° formado pelo ponto de coordenadas 2 da figura 2, sendo
o valor da ordenada 0,5. O valor da abscissa é igual ao co-seno de 30° = 0,866.
Principais valores constantes. As figuras 2, 3, 4, 5 e 6 dão os valores constantes das orde-
nadas e abscissas de circunferências de raio 1 que são divididas em doze, dezesseis, vinte e
quatro, trinta e dois e quarenta partes iguais, respectivamente.
Cálculo das grandezas reais das linhas B2 e B4(fig1). As grandezas reais destas linhas são
calculadas aplicando o TEOREMA DE PITÁGORAS, já que a linha B2 é a hipotenusa de um tri-
ângulo retângulo cujos catetos são iguais à projetante 2-2’ e à projeção B2’.
A linha B2’ é a hipotenusa do triângulo retângulo B2’D. O cateto D2’ é igual à altura H do
transformador e o cateto BD é igual à diferença que existe entre a metade do lado da base
(BC) do transformador e o comprimento da abscissa2, sendo esta 0,866r.
O valor da projetante 2-2’ pode ser obtido diminuindo da metade da largura da base
(AB) o comprimento da ordenada 2 (AB – 0,5r).
Para achar a grandeza real da linha B2, somam-se os quadrados de BD, 2-2’ e H e depois
extrai-se a raíz quadrada.

5. Os exemplos que foram expostos dão uma idéia clara de como se pode calcular as
grandezas reais das linhas de qualquer corpo.
Obtenção da Linha B1:

6. Obtenção da linha B2:
Obtenção da linha B3:

7. Obtenção da linha B4:
Planificação:

8. Conclusão: Fórmula geral para a obtenção das geratrizes.
Modelagem: