Pratica 5-clauder-eugenio-e-guilherme-martins
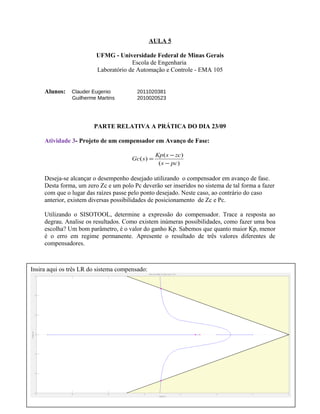
- 1. AULA 5 UFMG - Universidade Federal de Minas Gerais Escola de Engenharia Laboratório de Automação e Controle - EMA 105 Alunos: Clauder Eugenio 2011020381 Guilherme Martins 2010020523 PARTE RELATIVA A PRÁTICA DO DIA 23/09 Atividade 3- Projeto de um compensador em Avanço de Fase: )( )( )( pcs zcsKp sGc − − = Deseja-se alcançar o desempenho desejado utilizando o compensador em avanço de fase. Desta forma, um zero Zc e um polo Pc deverão ser inseridos no sistema de tal forma a fazer com que o lugar das raízes passe pelo ponto desejado. Neste caso, ao contrário do caso anterior, existem diversas possibilidades de posicionamento de Zc e Pc. Utilizando o SISOTOOL, determine a expressão do compensador. Trace a resposta ao degrau. Analise os resultados. Como existem inúmeras possibilidades, como fazer uma boa escolha? Um bom parâmetro, é o valor do ganho Kp. Sabemos que quanto maior Kp, menor é o erro em regime permanente. Apresente o resultado de três valores diferentes de compensadores. Insira aqui os três LR do sistema compensado:
- 2. Insira aqui as três expressões do compensador 1º compensador = 2º compensador = 3º compensador =
- 3. Insira aqui as três respostas ao degrau. Analise os resultados. 1ª resposta tp = 0.65 overshoot = 11.6 kp = 11.558 final value = 0.852 erro = 0.148 (46.25%) 2ª resposta tp= 0.488 overshoot= 16.4 kp= 21.236 final value= 0.914 erro= 0.086 (26.875%)
- 4. ANÁLISE A partir da análise dos 3 lugares das raízes compensados pode-se perceber que ao se distanciar o zero do compensador dos polos originais não compensados, fez-se com que as raizes obtidas que seguem as especificações passassem a se concentrar cada vez mais perto dos polos originais. E, também com o maior distanciamento do polo e zero do compensador dos polos do lugar das raizes original, obteve-se uma melhor reposta, que atendesse à especificação, a custo de uma mudança cada vez maior no aspecto do lugar das raízes. Obersando-se a resposta ao degrau percebe-se que para uma constante diminuição do erro em regime permanente basta aumentar o valor de Kp, o que consequentemente tambem diminui o tempo de pico, a custo de um crescente aumento no sobre-sinal, o que não é desejado muitas vezes. Portanto, é necessario que se busque um valor adequado de Kp, para que mesmo possa melhorar a resposta ao degrau que atenda a especificação, mas que não interfira em muito no regime transitório. 3ª resposta tp=0.395 overshoot= 19.3 kp= 31.282 final value= 0.94 erro= 0.06 (18.75%)
- 5. PARTE RELATIVA A PRÁTICA DO DIA 30/09 Objetivo : Projetar um compensador PI ou PID e simular o sistema de controle em malha fechada utilizando o sisotool Considere o sistema de controle em malha fechada representado abaixo: Pode-se projetar o compensador em quatro etapas: Primeira etapa: Define-se o desempenho desejado. Este método é muito eficiente quando as especificações de desempenho desejado são dadas em termos de grandezas no domínio do tempo tais como, coeficiente de amortecimento e frequência natural amortecida dos pólos dominantes da malha fechada, máximo sobresinal, tempo de subida, tempo de acomodação, etc. Segunda etapa: Traça-se o LR da planta para analisar o desempenho do sistema sem o compensador , ou seja, neste caso o compensador será do tipo proporcional. Baseado no desempenho desejado, determina-se o pólo desejado (sd). Caso o LR original não atenda às especificações desejadas (ou seja, nenhum ramo passe pelo pólo desejado), inicia-se o cálculo do compensador. Terceira etapa – utilizando o sisotool. O comando sisotool permite que se encontre o compensador. Para isso, basta inserir um pólo na origem (integrador), e em seguida, por tentativa, determinar o lugar geométrico do(s) zero(s) que fará(ão) com que o ramo passe pelo pólo desejado. Quarta etapa: obtém-se o valor de Kp que fornece o comportamento desejado. Resposta c(t) m(t)Erro e(t) Referência - + Planta Gp(s) GCPID (s)
- 6. ATIVIDADE 1 - PROJETO DE UM COMPENSADOR PI 1- Projete um compensador PI de tal forma que o erro em regime permanente se anule, o sobressinal seja de 15% e o tempo de pico seja reduzido em aproximadamente 30% em relação ao sistema sem compensador. Seguir o seguinte procedimento: a – Considere o controlador proporcional e através do LR, e ajuste o controlador proporcional de forma que o sobresinal seja de 15%. Trace a resposta ao degrau, para o sistema em malha fechada. Determine o tempo de pico e os pólos de malha fechada. b- Determine o tempo de pico desejado e o pólo de malha fechada desejado. c- Utilize o sisotool para obter o compensador que possibilite que a situação desejada ocorra. Tente pelo menos três valores diferentes de zero. d- Trace a resposta ao degrau para o sistema com o compensador projetado e compare com a resposta ao degrau obtida anteriormente. Comente os resultados. Tempo de pico do sistema sem compensação PID : 1.57 Ganho proporcional para sobresinal de 15% : 6.385 Tempo de pico desejado : 1.09 Apresente os seguintes resultados: - LR para sistema não compensado s zcs KsG cc − =)(
- 7. - LR para sistema compensado (Zc1, Zc2 e Zc3)
- 8. - Apresente os três compensadores obtidos compensador 1 = 2,5358x(1 +1.3s)/s compensador 2 = 2.7665x(1 + 1s)/s compensador 3 = 0.38247x(1 + 11s)/s - Apresente a resposta ao degrau para os três compensadores
- 9. - Conclusão Percebe-se que como o erro em regime permanente ja está designado como zero, devido ao termo integrador na origem, as outras caracteristicas da reposta sao modificadas com diferentes valores dos zeros e do ganho Kp, sendo que um aumento desse ganho melhora o tempo de resposta, mas aumenta o sobressinal. Ressalta-se tambem, que devido as características dos polos da FTMA, não foi possivel atender às especificações pedidas.
- 10. ATIVIDADE 2 - PROJETO DE UM COMPENSADOR PID A função de transferência do compensador PID pode ser representada da seguinte forma: s ZsZs KsK s K KsG cc pD I pCPID ))(( )( 21 ++ =++= ATIVIDADE 1 Adotando o procedimento descrito acima (com o uso do sisotool), calcule um compensador PID que: 1- Anule o erro em regime permanente; 2- Mantenha um sobresinal de aproximadamente 15%. E que para este sobresinal, o tempo de pico da resposta ao degrau do sistema em malha fechada, do sistema compensado, seja reduzido em 30% quando comparado com o sistema sem compensador PID. Apresente os seguintes resultados: - LR para sistema não compensado
- 11. - LR para sistema compensado ( três possibilidades);
- 12. - Apresente, os três compensadores obtidos 1º compensador: k = 18.562 tp = 0.99 overshoot = 14.9 Expressão: 18.562x(1 +0.71s + (0.4s)^2)/s 2º compensador k = 2224.2 tp = 0.104 overshoot = 12.9 Expressão: 2224.2x(1 + 0.22s = (0.14s)^2)/s 3º compensador: k = 42.939 tp= 0.715 overshoot= 10.5 Expressão: 42.939x(1 + 0.58s + (0.4s)^2)/s
- 13. - Apresenta a resposta ao degrau para os três compensadores
- 14. - Conclusão e comparação com o caso anterior. Comparando-se com o caso anterior, pode-se perceber que a adição de polos complexos conjugados melhora a resposta do sistema, fazendo com que ele obdedeça as especificações, algo que nao havera sido possivel na parte anterior. Analisando os lugares das raízes e as respostas ao degrau, percebemos que quanto mais distantes esses zeros se encontram do eixo real, maior o ganho correspondente e menor o tempo de pico, representando assim uma boa resposta às especifações, sem que haja grande influência no transitório. Vale ressaltar ainda, que o segundo caso, apesar de apresentar a resposta mais rapida, seria inviavel do ponto de vista prático, uma vez que o altíssimo valor do ganho exigira uma grande potencia desprendida pelo sistema de controle, o que muitas vezes não é economicamente viável ou até mesmo fisicamente possível.