Unidade 8

Unidade 8
. O Modelo simplificado de Sharpe (1963)
Avaliação de activos financeiros: Modelo C.A.P.M.
(Notas de Moukhamedjanova Sabina
Chan Bonnie e de
Abhishek Kapur & Geir Sivertsen)
Carlos Arriaga Economia Bancária e financeira 1

.Bibliografia
 Eugene F. Fama e Merton H. Miller The
Theory of Finance (Hinsdale, Illinois:
Dryden Press, 1972) Cap 7.

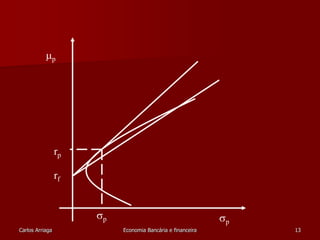
Eficiência segundo Markowitz – baseado na média e
na variância
Considere N activos num portfolio e as
seguintes notações :
Vector de ponderações w=[w1 . . . wN]
Matriz das variâncias-covariâncias Ω
Vector de retornos R=[R1 . . . RN]
Vector unitário 1=[11 . . . 1N]
Variância do portfólio wT Ω w
Retorno do portfólio wT R

Fronteira do Portfolio
Retornos do portfolio : wT R
Variância do Portfolio : wT Ω w
1
2
3
4 6
5

Efficiencia segundo Markowitz
(Média-Var)
1=1T w
Para encontrar a fronteira de eficiência
s.a.
r=RT w
min wT Ω w
w
Optimização :
min wT Ω w + (1-1T w) + (r-
1
2
RT w) w

Eq. 1 : Ωw=1 + R
Eq. 2 :w=Ω-11 + Ω-1 R
Multiplicando equação 1 por 1T e RT :
Eq. 3 :1=a  +b 
Eq. 4 : r=b  +c 
onde : a=1T Ω-11, b=1T Ω-1R, c=RT Ω-1R
FOC :

Resolvendo em ordem a  e  nas equações 3 e 4,
e substituindo na eq 2, obtem-se :
w=v1+v2 r
V1 e v2 são dois vectores fixos.
Por outro lado, qualquer combinação convexa de
portfolios eficientes é também um portfolio
eficiente.
O portfolio de mercado não é mais do que uma
combinação ponderada de portfólios, e que,por
sua vez também é eficiente.

Modelo simplificado de Sharpe
 Problemas do Modelo de Markowitz: Grande dimensão
da matriz de co-variâncias (cálculo computacional
complicado em 1959)
 Conhecimento da matriz das co-varâncias
 Hipótese de Sharpe (1963): Os rendimentos dos diversos
activos encontram-se ligados entre eles por uma relação
a um factor comum subjacente:
 Ři = αi + βi Ĩ + ũi
 Ĩ = αn+1+ vn+1

CAPM
– Mossin, Jan. “Equilibrium in a Capital Asset
Market.” Econometrica 34(Oct. 1966): 768-83.
– Sharpe, W. F. “Capital Asset Prices: A Theory
of Market Equilibrium under Conditions of
Risk.” Journal of Finance 19(Sept. 1964): 425-
42.

– Lintner, John. “Security Prices, Risk, and
Maximal Gain from Diversification.” Journal of
Finance 20(Dec. 1965): 587-615.
– Lintner, John. “The Valuation of Risk Assets
and the Selection of Risky Investments in
Stock Portfolios and Capital Budgets.” Review
of Economics and Statistics 47(Feb. 1965):
13-37.

Avaliação de activos financeiros: Modelos C.A.P.M.
e A.P.T.
 Capital market theory (derivado do modelo de Sharpe)
 SEcurity market line: Determinação do valor de um activo, tendo em
conta o activo sem risco e o portfólio de mercado.
 CAPM : Capital Asset Pricing Market: Modelo de avaliação dos
activos financeiros tendo em conta a relação entre o modelo de
mercado e a security market line.
 APT: Arbitrage Pricing theory : Os rendimentos dos cativos
financeiros são função lineares de mais do que um factor

O papel do activo sem risco no
modelo
 O equilíbrio de mercado oferece
dificuldades de representação porque
diferentes investidores têm assumpções
diferentes quanto ao risco. A introdução
do activo sem risco resolve esta
ambiguidade.
– O activo sem risco reduz o número potencial
de portfolios eficientes a um único portfolio.

sp
mp
rp
rf
sp

– Dentro deste equilíbrio, existe apenas um
portfolio eficiente. Qualquer grau de aversão
ao risco pode ser retratado no modelo através
de uma combinação de um portfolio simples e
eficiente e um emprestimo ou emprestar
(borrowing ou lending) à taxa sem risco.
– Substituindo xm por xp ou deixando que o
“portfolio índice” seja o portfolio de mercado
eficiente, ter-se-á:








s
m
1
m m ~
  m
j m x




j
s

1
 

r
m f s
m
m
1


1

r
 m

m f
m ~
s
m
r


 m

m f
s
m
r
 
j f
 
f









s

s
s
f j  m f 
m
j
x
jm
m
r
r r
   m

jm
s
 
j s
2
m
it i mt it r   r 

Conceitos
Borrowing Portfolio
 Um investidor é capaz de se endividar de
maneira a comprar um montante de um
portfólio cujo valor seja superior aos
valores iniciais:
 E(Řp) = Xzrz + (1-Xz)rb
 rb é a taxa de empréstimo

Conceitos
Lending portfolio
 Emprestador sobre o mercado monetário (sem risco) e
associação à aquisição de activos com risco.
 Condições :
 - Existe ao menos alguem que não apresenta risco de
não cumprimento da dívida (quem pede emprestado
com risco nulo)
- O rendimento presente e futuro de quem adquire este
activo é um valor certo
- Este activo oferece uma protecção perfeita contra a
perda do poder de compra

MODELO CAPM
O CAPM considera que todos os investidores possuem portfolios
eficientes no sentido de maior valor esperado para um mínimo
risco.
Pelo teorema de separação de dois portfolios, o portfólio de
mercado é também eficiente.
Para a validade do CAPM, o portfolio de mercado deve encontrar-se
na fronteira eficiente.

Condições de estimação do modelo de mercado
 O índice de mercado deverá responder às
condições seguintes:
 1. Ser exaustivo , isto é, deverá ser calculado a
partir de todos os activos financeiros com risco
existente no mercado (vinte são representativos)
 2. Ser um indice de rendimento e não apenas
um índice de preços. Deverá ter em conta os
rendimentos líquidos distribuídos (dividendos e
juros).
 3. Ser um índice ponderado e não uma média
aritmética simples.

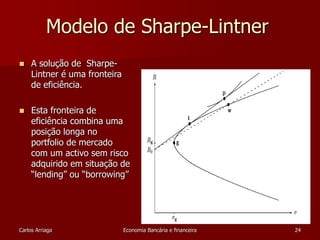
Versões do CAPM
Sharpe-Lintner :
Este activo assume a presença de um
Black :
E[Zi]=i + ßi (E[Zm])
Activo sem risco
E[Ri]=  i + ßi (E[Rm])
Este modelo trata a taxa sem risco como uma variável
aleatória

Problema de minimização
 Black version
w Vw w R w R T T
min s.t. 1 1 and T
w RN
 

 Sharpe-Lintner (com activo sem risco)
min w T Vw s.t. ( R
 R 1) T
w  R 
R N
0 0 w 
RCarlos Arriaga Economia Bancária e financeira 22

Sharpe Model
 Regressão de Zit sobre Zmt
 Hipótese nula :
0 0  
Versão de Black
 Regressão
[ ]  [ ]  ( ) [ ] t mt mt E R  i  E R   i   E R
 Hipótese nula α = (i-β)γ

Modelo de Sharpe-Lintner
 A solução de Sharpe-
Lintner é uma fronteira
de eficiência.
 Esta fronteira de
eficiência combina uma
posição longa no
portfolio de mercado
com um activo sem risco
adquirido em situação de
“lending” ou “borrowing”

Black CAPM
( ) p z (m) pm m z (m) R  R   R  R
p pm z m pm m R   R   R ( ) (1 )

Security Market Line
 E(Rp)
 E(rm)

y
 rf

Zero Beta Portfolio

 1 σ (p)

Security Market Line
• Derivamos a security
market line:
( ) 0 0 R R R R p pm m    
• Em forma de retorno
em excesso
R R R R
  
(  ) 0 0
p pm m
Z 

Z
it pm mt

Como testar o CAPM?
Os testes do CAPM focam-se em três implicações do modelo
de excesso de retorno
 A intercepção é zero
 Beta captura completamente a variação dos
retornos em excesso.
 O prémio de mercado é positivo.

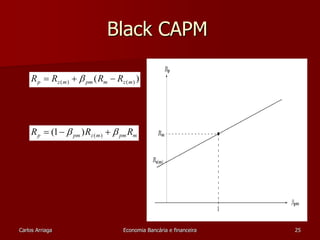
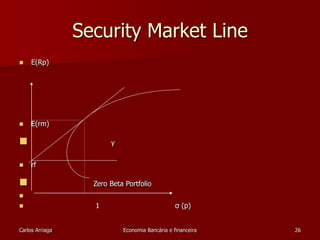
Testes sobre a “intercept”
Sharpe-Lintner :
E[Zi]=  i + ßi (E[Zm])
Testar se  i = 0
Black :
E[Ri]=  i + ßi (E[Rm])
Testar se
 i = (1-ßi) E[R0]

Zero-Beta CAPM

Pressupostos implicitos do modelo
As estimativas encontram-se sujeitas a erro de
amostragem pelo que o portfolio de mercado não é
suposto ser ex-post eficiente.
A medida do racio de sharp mede a ineficiencia do
portfolio de mercado que nos permite detrminar quando
deveremos rejeitar o CAPM.

Rácio de Sharpe
Dada uma tangente a, e um
portfolio de mercado m :
a
ineficiência de m m
rf
A diferença ra - rm dá-nos
uma medida da

Oferta de acções pela empresa
 Assumimos que cada empresa vende acções a
um preço Pi. Os Investidores desejam adquirir
estas acções fundamentados no valor futuro da
empresa no final do período, Vi. O valor de
aquisição e o valor da empresa no final do
período determinarão a taxa de retorno:
V 
P
i i
R

i P
i

O valor futuro da empresa implica algum risco,
por isso a taxa de retorno possui risco. Por
outro lado, todos os investidores avaliam o
investimento considerando o equilibrio da linha
de “capital market”.
 Matematicamente, o preço e o valor do portfolio
de mercado fica:
N
N
 
 
P  P V 
V
m i m i
i
i
e
1 1

Medidas de Performance baseadas no APT
 Modelo de dois factores
A E(r ) (E(r ) + [E(I ) E(r )]β [E(I ) E(r )]β ) p p Z 1 Z 1,p 2 Z 2,p     
 Nota: A medida é semlhante ao índice
de Jensen Index.

Conclusão
 No caso do CAPM não se sabe se a
performance é drivado à habilidade do
investidor ou à ineficiência do índice de
mercado. No modelo APT, existe
liberdade de seleccionar os factores sem
restrição, pelo que a performance tem
em conta os factores que considerámos.

Unidade 8

Mais conteúdo relacionado

Semelhante a Unidade 8

Unidade 8