1. Introdução a estruturas de dados, incluindo Tipos de Dados Abstractos (TDA), ponteiros, funções e estruturas definidas pelo programador.
2. Listas lineares como listas sequenciais, ligadas, circulares e duplamente ligadas e implementações de pilhas e filas.
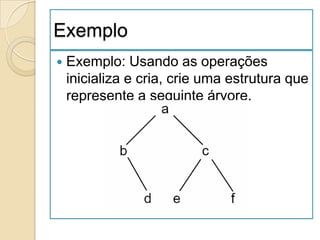
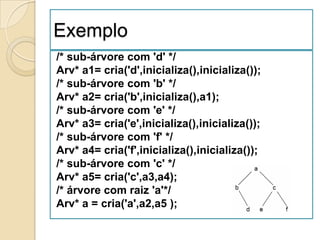
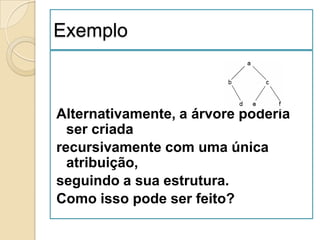
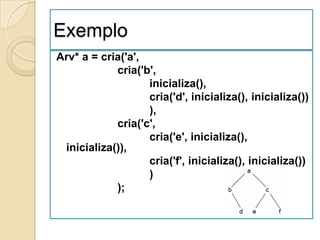
3. Árvores, incluindo representação, terminologia e tipos como binárias e balanceadas.
4. Ordenação com métodos como seleção, inserção, shellsort e quicksort.
5. Pesquisa com métodos sequencial, binária e em








![TDA-Exemplo
//definição de valor
abstract typedef <integer, integer> RACIONAL;
condiction RACIONAL [1] <> 0;
//definição de operador
abstract RACIONAL criaracional(a, b)
int a, b;
precondition b <> 0;
postcondition criaracional[0]== a;
criaracional[1]== b;
abstract RACIONAL soma (a, b)
RACIONAL a, b;
postcondition soma[1]== a[1]*b[1];
soma[0]==a[0]*b[1]+b[0]*a[1];](https://image.slidesharecdn.com/ed1-120926011938-phpapp01/85/Ed1-9-320.jpg)
![abstract RACIONAL mult(a, b)
RACIONAL a, b;
postcondition mult[0]==a[0]*b[0];
mult[1]==a[1]*b[1];
abstract RACIONAL igual(a,b)
RACIONAL a, b;
postcondition igual==(a[0]*b[1]==a[1]*b[0]);
Exercício:
Crie o TODA para o conjunto de números complexos com todas
as suas operações básicas.](https://image.slidesharecdn.com/ed1-120926011938-phpapp01/85/Ed1-10-320.jpg)










![Estrutura de dados e tipo de dados definido pelo
utilizador
Estruturas são peças contíguas de armazenamento que contém
vários tipos simples agrupados numa entidade.
Estrutura são manifestadas através da palavra reservada struct
seguida pelo nome da estrutura e por uma área delimitada por
colchetes que contém campos.
struct pessoa {
char nome[30];
int idade;
char sexo;
};
Para criação de novos tipos de estrutura de dados utiliza-se a
palavra-chave: typedef
typedef struct pessoa {
char nome[30];
int idade;
char sexo;
} PESSOA;](https://image.slidesharecdn.com/ed1-120926011938-phpapp01/85/Ed1-21-320.jpg)





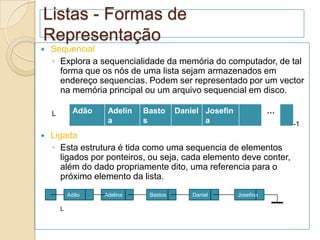
![Listas sequenciais
Uma lista representada de forma sequencial é um
conjunto de registos onde estão estabelecidas
regras de precedência entre seus elementos.
Implementação de operações pode ser feita
utilizando array e registo, associando o elemento a[i]
com o índice i.
Características
◦ Os elementos na lista estão armazenados
fisicamente em posições consecutivas
◦ A inserção de um elemento na posição a[i] causa
o deslocamento a direita do elemento a[i] ao
último.
◦ A eliminação do elemento a[i] requer o
deslocamento à esquerda do a[i+1] ao último.](https://image.slidesharecdn.com/ed1-120926011938-phpapp01/85/Ed1-28-320.jpg)

![Listas sequenciais
Operações básicas
Definição
#define MAX 50 //tamanho máximo da lista
typedef char elem[20]; // tipo base dos elementos da lista
typedef struct tlista{
elem v[MAX];//vector que contém a lista
int n; //posição do último elemento da lista
};
Tlista
Adão Alberto Ana Daniela Carmen …
n=5 v
0 1 2 3 4 5 6 MAX – 1
1.Criar uma lista vazia 2. Verificar se uma lista está vazia
void criar(tlista *L) { int vazia(tlista L) {
L -> n = 0; return (L .n == 0);
} }](https://image.slidesharecdn.com/ed1-120926011938-phpapp01/85/Ed1-30-320.jpg)
![Listas sequenciais
Operações básicas
3. Verificar se uma lista está cheia 4. Obter o tamanho de uma lista
int cheia( tlista L) { int tamanho ( tlista L){
return (L .n == MAX); return (L.n);
} }
5. Obter o i-ésimo elemento de uma 6. Pesquisar um dado elemento,
lista retornando a sua posição.
int elemento( tlista L, int pos, elem *dado ) int posicao( tlista L, elem dado )
{ {
if ((pos > L.n) || (pos <=0)) int i;
return (0); for (i=1; i<L.n; i++)
*dado = L.v [pos - 1]; if(L.v[i-1] == dado)
return 1; return i;
} return 0;
}](https://image.slidesharecdn.com/ed1-120926011938-phpapp01/85/Ed1-31-320.jpg)
![Listas Sequenciais
Operações básicas
7. Inserção de um elemento em uma 8. Remoção do elemento de uma
determinada posição determinada posição
(requer o deslocamento à direita dos (requer o deslocamento à esquerda dos
elementos v(i+1) … v(n)) elementos v(p+1) … v(n))
// retorna 0 se a posição for inválida ou se a /* o parâmetro dado irá receber o elemento
lista encontrado.
// estiver cheia, caso contrário retorna 1 Retorna 0 se a posição for inválida , caso
contrário
retorna 1 */
int inserir( tlista *L, int pos, elem dado )
{
int i; int remover( tlista *L, int pos, elem *dado )
if (( L->n == MAX) || ( pos > L->n + 1 )) {
return (0); int i;
for (i = L->n; i >= pos; i--) if ( ( pos > L->n) || (pos <= 0) )
L->v[i] = L->v [i-1]; return (0);
L->v[pos-1] = dado; *dado = L-> v[pos-1];
(L->n)++; for (i = pos; i <= (L->n) - 1; i++)
return (1); L->v[i-1] = L->v [i];
} (L->n)--;
return (1);
}](https://image.slidesharecdn.com/ed1-120926011938-phpapp01/85/Ed1-32-320.jpg)















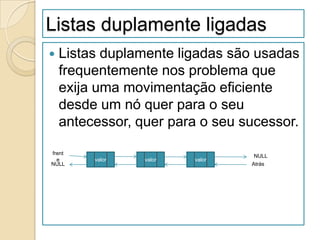









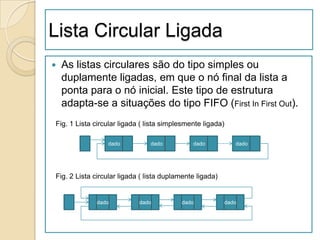




![Pilhas
Pilhas são listas onde a inserção ou a
remoção de um item é feita no topo.
Definição:
dada a pilha P= (a[1], a[2], …, a[n]),
dizemos que a[1] é o elemento da base da
pilha; a[n] é o elemento topo da pilha; e
a[i+1] está acima de a[i].
Pilhas são conhecidas como listas LIFO
(last in first out)](https://image.slidesharecdn.com/ed1-120926011938-phpapp01/85/Ed1-63-320.jpg)


![Implementação Sequencial
#define MAXPILHA 50
#define tpilha(p) (p->topo – p->base)
typedef struct pilha{
int base[MAXPILHA];
int *topo;
}PILHA;](https://image.slidesharecdn.com/ed1-120926011938-phpapp01/85/Ed1-66-320.jpg)








![Implementação de Filas em C
Usamos o vector para armazenar os
elementos da fila e duas variáveis, inic e fim,
para armazenar as posições dentro do vector
do primeiro e último elementos da fila:
#define MAXFILA 100
struct fila{
int elem[MAXFILA];
int inic, fim;
}f;
É evidente que usar vector para armazenar
uma fila introduz a possibilidade de estouro,
caso a fila fique maior que o tamanho do
vector.](https://image.slidesharecdn.com/ed1-120926011938-phpapp01/85/Ed1-75-320.jpg)




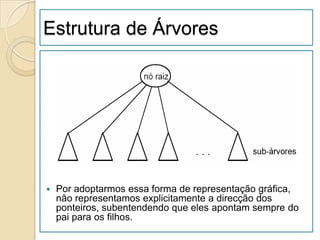


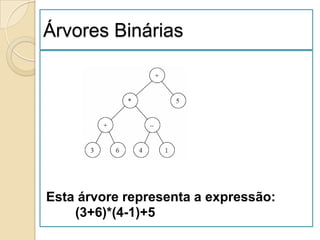

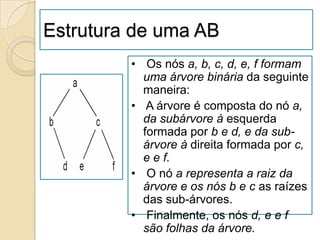

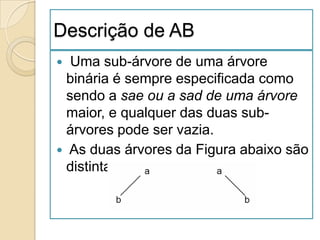







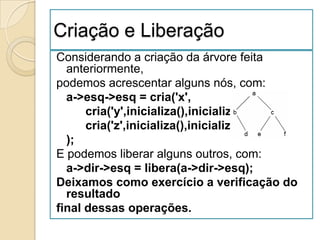



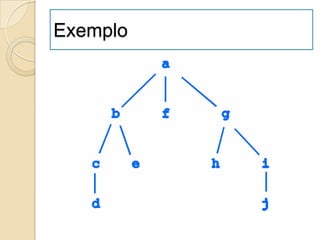


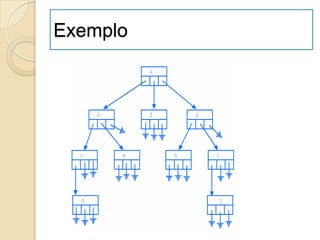


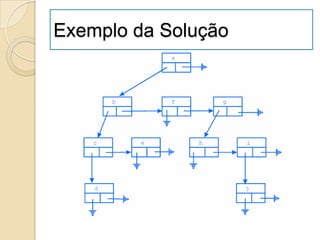



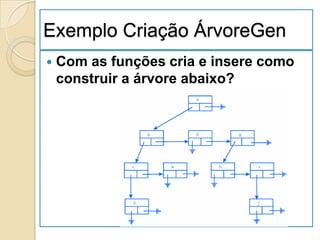


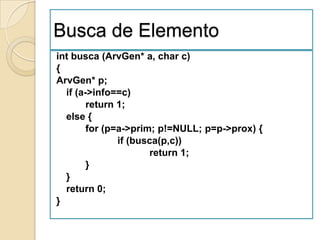











![Ordenação por Selecção
void selectionSort(int vector[],int tam) {
int i, j, min, aux;
for(i=0; i<tam-1; i++) {
min = i;
aux = vector[i];
for(j=i+1; j<tam; j++) {
if (vector[j] < aux) {
min=j; aux=vector[j];
}
}
aux = vector[i];
vector[i] = vector[min];
vector[min] = aux;
}
}
129](https://image.slidesharecdn.com/ed1-120926011938-phpapp01/85/Ed1-129-320.jpg)
![Código da ordenação SelectionSort com strings
void ordenar_seleccao() {
int j;
for(i=0; i<n-1; i++) {
for(j=i+1; j<n; j++) {
if(strcmpi(vector[i], vector[j])>0) {
strcpy(aux_char, vector[i]);
strcpy(vector[i], vector[j]);
strcpy(vector[j], aux_char);
}
}
}
}](https://image.slidesharecdn.com/ed1-120926011938-phpapp01/85/Ed1-130-320.jpg)

![void bubble( int v[], int qtd ) {
int i; int j, aux, k = qtd - 1 ;
for(i = 0; i < qtd; i++) {
for(j = 0; j < k; j++) {
if(v[j] > v[j+1]) {
aux = v[j];
v[j] = v[j+1];
v[j+1]=aux;
}
}
}
}](https://image.slidesharecdn.com/ed1-120926011938-phpapp01/85/Ed1-132-320.jpg)
![void swapbubble( int v[], int i ) {
aux = v[i];
v[i] = v[i+1];
v[i+1]=aux;
}
void bubble( int v[], int qtd ) {
int i,j;
for( j = 0; j < qtd; j++ ) {
for( i = 0; i < qtd - 1; i++ ) {
if( v[i] > v[i+1] ) {
swapbubble( v, i );
}
}
}
}](https://image.slidesharecdn.com/ed1-120926011938-phpapp01/85/Ed1-133-320.jpg)
![ Método de ordenação Bolha com ordenação de strings.
void bubble(int v[], int qtd){
int i, trocou;
char aux;
do {
qtd--;
trocou = 0;
for(i = 0; i < qtd; i++)
if(strcasecmp(v[i],v[i + 1])>0) {
strcpy(aux, v[i]);
strcpy(v[i], v[i + 1]);
strcpy(v[i + 1], aux);
trocou = 1;
}
}while(trocou==1);
}](https://image.slidesharecdn.com/ed1-120926011938-phpapp01/85/Ed1-134-320.jpg)
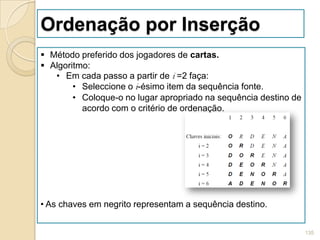
![Ordenação por Inserção
void insertionSort(int vector[], int tam) {
int i, j; int key;
for (j = 1; j < tam; ++j) {
key = vector[j];
i = j - 1;
while (vector[i] > key && i >= 0) {
vector[i+1] = vector[i];
--i;
}
vector[i+1] = key;
}
}
A colocação do item no seu lugar apropriado na
sequência destino é realizada movendo-se itens com
chaves maiores para a direita e então inserindo o item
na posição deixada vazia.
136](https://image.slidesharecdn.com/ed1-120926011938-phpapp01/85/Ed1-136-320.jpg)





![Shellsort
void shellsort ( Int v [ ] , int n) {
int i,j,x,h = 1;
do h = h *3 + 1;
while (h < n) ;
do {
h /= 3;
for ( i = h + 1; i <= n; i ++) {
x = v[ i ] ; j = i ;
while (v[ j − h] > x > 0) {
v[ j ] = v[ j − h] ; j −= h;
i f ( j <= h) break;
}
v[ j ] = x;
}
} while (h != 1) ;
}
A implementação do Shellsort não utiliza registos
sentinelas.
Seriam necessários h registos sentinelas, uma para
cada h-ordenação. 142](https://image.slidesharecdn.com/ed1-120926011938-phpapp01/85/Ed1-142-320.jpg)


![Quicksort
A parte mais delicada do método é relativa ao método
partição.
O vector v[esq..dir ] é rearranjado por meio da escolha
arbitrária de um pivô x.
O vector v é particionado em duas partes:
• A parte esquerda com chaves menores ou
iguais a x.
• A parte direita com chaves maiores ou iguais a
x.
145](https://image.slidesharecdn.com/ed1-120926011938-phpapp01/85/Ed1-145-320.jpg)
![Quicksort
Algoritmo para o particionamento:
1. Escolha arbitrariamente um pivô x.
2. Percorra o vector a partir da esquerda até que v[i]
x.
3. Percorra o vector a partir da direita até que v[j] x.
4. Troque v[i] com v[j].
5. Continue este processo até os apontadores i e j se
cruzarem.
• Ao final, o vector v[esq..dir ] está particionado de
tal forma que:
• Os itens em v[esq], v[esq + 1], . . . , v[j] são
menores ou iguais a x.
• Os itens em v[i], v[i + 1], . . . , v[dir ] são
maiores ou iguais a x.
146](https://image.slidesharecdn.com/ed1-120926011938-phpapp01/85/Ed1-146-320.jpg)
![Quicksort
• Ilustração do processo de partição:
O pivô x é escolhido como sendo v[(i+j) / 2].
Como inicialmente i = 1 e j = 6, então x = v[3] = D.
Ao final do processo de partição i e j se cruzam em i =
3e j = 2.
147](https://image.slidesharecdn.com/ed1-120926011938-phpapp01/85/Ed1-147-320.jpg)
![Quicksort
void swap(int* a, int* b) {
int tmp;
tmp = *a;
*a = *b;
*b = tmp;
}
int partition(int vec[], int left, int right) {
int i, j;
i = left;
for (j = left + 1; j <= right; ++j) {
if (vec[j] < vec[left]) {
++i;
swap(&vec[i], &vec[j]);
}
}
swap(&vec[left], &vec[i]);
return i;
}
148](https://image.slidesharecdn.com/ed1-120926011938-phpapp01/85/Ed1-148-320.jpg)
![Quicksort
Método ordena e algoritmo Quicksort :
void quickSort(int vec[], int left, int right) {
int r;
if (right > left) {
r = partition(vec, left, right);
quickSort(vec, left, r - 1);
quickSort(vec, r + 1, right);
}
}
149](https://image.slidesharecdn.com/ed1-120926011938-phpapp01/85/Ed1-149-320.jpg)
![ Implementação usando 'fat pivot':
void sort(int array[], int begin, int end) {
int pivot = array[begin];
int i = begin + 1, j = end, k = end, t;
while (i < j) {
if (array[i] < pivot) i++;
else if (array[i] > pivot) {
j--;
k--;
t = array[i];
array[i] = array[j];
array[j] = array[k];
array[k] = t;](https://image.slidesharecdn.com/ed1-120926011938-phpapp01/85/Ed1-150-320.jpg)
![} else {
j--;
swap(array[i], array[j]);
}
}
i--;
swap(array[begin], array[i]);
if (i - begin > 1)
sort(array, begin, i);
if (end - k > 1)
sort(array, k, end);
}](https://image.slidesharecdn.com/ed1-120926011938-phpapp01/85/Ed1-151-320.jpg)

![void ordenar_quicksort(int ini, int fim) {
int i = ini, f = fim;
char pivo[50];
strcpy(pivo,vector[(ini+fim)/2]);
if (i<=f) {
while (strcmpi(vector[i],pivo)<0)
i++;
while (strcmpi(vetor[f],pivo)>0)
f--;
if (i<=f) {
strcpy (aux_char,vetor[i]);
strcpy (vetor[i],vetor[f]);
strcpy (vetor[f],aux_char);
i++; f--;
}
}](https://image.slidesharecdn.com/ed1-120926011938-phpapp01/85/Ed1-153-320.jpg)




![Heaps
É uma sequência de itens com chaves c[1], c[2], . . .
, c[n], tal que:
c[i] c[2i],
c[i] c[2i + 1], para todo i = 1, 2, . . . , n/2.
A definição pode ser facilmente visualizada em uma
árvore binária completa:
árvore binária completa:
• Os nós são numerados de 1 a n.
• O primeiro nó é chamado raiz.
• O nó k/2 é o pai do nó k, para 1 < k n.
• Os nós 2k e 2k + 1 são os filhos à esquerda e à
direita do nó k, para 1 k k/2
158](https://image.slidesharecdn.com/ed1-120926011938-phpapp01/85/Ed1-158-320.jpg)

![Heaps
Na representação do heap em um arranjo, a
maior chave está sempre na posição 1 do vector.
Os algoritmos para implementar as operações
sobre o heap operam ao longo de um dos
percursos da árvore.
Um algoritmo elegante para construir o heap foi
proposto por Floyd em 1964.
O algoritmo não necessita de nenhuma memória
auxiliar.
Dado um vector v[1], v[2], . . . , v[n].
Os itens v[n/2 + 1], v[n/2 + 2], . . . , v[n] formam um
heap:
• Neste intervalo não existem dois índices i e j
tais que j = 2i ou j = 2i + 1. 160](https://image.slidesharecdn.com/ed1-120926011938-phpapp01/85/Ed1-160-320.jpg)
![Heapsort
void heapsort(tipo a[], int n) {
int i = n/2, pai, filho;
tipo t;
for (;;) {
if (i > 0) {
i--;
t = a[i];
} else {
n--;
if (n == 0)
return;
t = a[n];
a[n] = a[0];
}
161](https://image.slidesharecdn.com/ed1-120926011938-phpapp01/85/Ed1-161-320.jpg)
![pai = i;
filho = i*2 + 1;
while (filho < n) {
if ((filho + 1 < n) && (a[filho + 1] >
a[filho]))
filho++;
if (a[filho] > t) {
a[pai] = a[filho];
pai = filho;
filho = pai*2 + 1;
} else break;
}
a[pai] = t;
}
} 162](https://image.slidesharecdn.com/ed1-120926011938-phpapp01/85/Ed1-162-320.jpg)
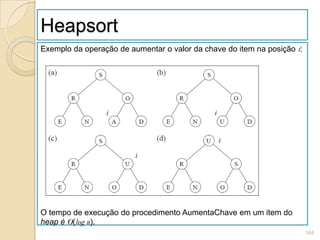
![Heapsort
Algoritmo:
Os itens de v[4] a v[7] formam um heap.
O heap é estendido para a esquerda (esq = 3), englobando o item
v[3], pai dos itens v[6] e v[7].
A condição de heap é violada:
• O heap é refeito trocando os itens D e S.
O item R é incluindo no heap (esq = 2), o que não viola a condição de
heap.
O item O é incluindo no heap (esq = 1).
A Condição de heap violada:
• O heap é refeito trocando os itens O e S, encerrando o
processo.
163](https://image.slidesharecdn.com/ed1-120926011938-phpapp01/85/Ed1-163-320.jpg)
![Construção de Heap
Algoritmo:
1. Construir o heap.
2. Troque o item na posição 1 do vector (raiz do heap)
com o item da posição n.
3. Use o procedimento Refaz para reconstituir o heap
para os itens v[1], v[2], . . . , v[n − 1].
4. Repita os passos 2 e 3 com os n − 1 itens restantes,
depois com os n − 2, até que reste apenas um item.](https://image.slidesharecdn.com/ed1-120926011938-phpapp01/85/Ed1-165-320.jpg)

