Este documento apresenta um roteiro de estudo introdutório sobre mecânica clássica. Ele destina-se principalmente a estudantes de física da Universidade Estadual do Ceará e fornece uma lista diversificada de exercícios para desenvolver habilidades analíticas. O autor convida reparos, críticas e sugestões para melhorar a proposta.

1. Apresentação
E ste trabalho constitui um roteiro básico de estudo. Portanto, não
substitui os títulos bibliográficos específicos de Mecânica Clássica
voltados para cursos de graduação nas Universidades brasileiras.
Acreditamos na sua utilidade como fonte de pesquisa teórica introdutória da
disciplina, a ser suplementada nos livros relacionados no final do texto,
dentre outros. Destina-se, principalmente, aos alunos do curso de Física
(bacharelado e licenciatura) da Universidade Estadual do Ceará. Além
disso, as notas aqui reunidas poderão ser aproveitadas, a qualquer tempo,
por aqueles que pretendam rever os tópicos conceituais ou explorar alguns
dos mais interessantes problemas de aplicação da mecânica.
O intuito maior foi o de reunir uma lista bem diversificada de questões
relativas ao movimento para que o aluno-leitor desenvolva a sua
capacidade analítica e adquira habilidade no emprego dos princípios e
teoremas que formam o alicerce desse importante ramo da Física.
Conhecimentos básicos de análise vetorial e cálculo diferencial e integral
são requisitos para uma compreensão satisfatória dos processos
relacionados ao movimento da partícula e a completa aplicação das leis de
Newton.
Reparos, críticas e sugestões para o aprimoramento da proposta serão
bem-vindos.
Professor Anísio Meneses
anisiomeneses@secrel.com.br
março/2004
1

2. Mecânica Básica I (cód. CT242)
Créditos: 6
Semestre: _____/_____
Programação:
Início: ___/___/_____
Término: ___/___/_____
Avaliações individuais:
1ª. : ___/___/_____
2ª. : ___/___/_____
3ª. : ___/___/_____
4ª. : ___/___/_____
Entrega de relatórios (listas de exercícios):
1º. : ___/___/_____
2º. : ___/___/_____
3º. : ___/___/_____
4º. : ___/___/_____
5º. : ___/___/_____
6º. : ___/___/_____
7º. : ___/___/_____
8º. : ___/___/_____
Seminário: ___/___/_____
2

3. Sumário
página
Introdução......................................................................................... 5
Grandezas físicas e medição........................................................... 10
Elementos de análise vetorial........................................................... 17
Conceitos fundamentais da mecânica.............................................. 28
Cinemática da partícula.................................................................... 32
As leis de Newton da dinâmica................................................ 78
Trabalho e energia........................................................................... 121
Leis de conservação......................................................................... 133
Impulso e quantidade de movimento................................................ 157
Colisões............................................................................................ 165
Listas de exercícios
1ª. Lista de exercícios................................................. 175
2ª. Lista de exercícios................................................. 177
3ª. Lista de exercícios................................................. 180
4ª. Lista de exercícios................................................. 185
5ª. Lista de exercícios................................................. 191
6ª. Lista de exercícios................................................ 195
7ª. Lista de exercícios................................................ 198
8ª. Lista de exercícios................................................ 205
3

4. 4

5. Introdução
A Mecânica se dedica ao estudo das condições de movimento de corpos
submetidos à ação de forças. Nessa simples definição, pelo menos dois
termos (movimento e força) somente se justificam a partir da necessidade
de sistematização de fenômenos muito comuns no cotidiano – os objetos se
aproximam ou se afastam uns dos outros. Corpos se movimentam quando
mudam de posição (E o que significa essa posição? Ela tem caráter
absoluto ou relativo?). Aclarar o significado disso é o nosso primeiro desafio.
Quando caminhamos, “somos empurrados” pelo chão para frente ou
“estamos empurrando” a Terra para trás? É o aluno que se dirige à escola
ou a escola que se dirige ao aluno? É o veículo que colide com o poste ou é
o poste que colide com o veículo? Percebemos que diversos e intrigantes
fenômenos (e novas questões) permeiam todos os acontecimentos, desde
aqueles mais prosaicos. E o que causa tudo isso? Qual o agente
responsável por toda essa dinâmica? Podemos especular, formular algumas
hipóteses, ensaiar conclusões. Não vemos qualquer força, porém qualquer
pessoa é capaz de reconhecer que elas “existem”, produzem efeitos visíveis
(alguns, assombrosos).
O tempo é outro conceito desafiador (perturbador, às vezes) – ele sempre
“anda” para frente; não raro, assume conotação um tanto quanto subjetiva
(o meu tempo, o seu tempo...). Os acontecimentos nunca se desenvolvem
instantaneamente – há sempre uma duração para qualquer ato, por mais
rápido que seja.
Para uma boa análise e descrição do fenômeno, precisamos avaliar,
quantificar. Em se tratando de movimento, é necessário medir o tempo, o
espaço, a velocidade, a aceleração, a força, um sem-número de variáveis.
Por outro lado, os instrumentos auxiliares à percepção humana são, todos
eles, limitados. E não há qualquer expectativa de, em algum tempo futuro,
se tornarem absolutamente precisos. Com efeito, tudo é relativo: depende
do modelo, do observador e de seus mecanismos de avaliação.
É nessa perspectiva de compreender fenômenos que nascem diversos
conceitos1, muitos dos quais não absolutamente naturais. Afinal, são
diversas as maneiras que temos de ver e encarar o mundo. Modelos se
1 Conceito é a representação de um objeto pelo pensamento, por meio de suas
características gerais. É também a formulação de uma idéia por meio de palavras (conforme
Dicionário Aurélio).
5

6. sucedem, adquirem maior sofisticação, porém ainda estão longe de
reproduzir todas as singularidades de um sistema natural.
Podemos, numa síntese, propor: não sabemos o que preside, de fato, o
funcionamento da natureza, como são preparadas suas ações e respostas,
porém já dispomos, hoje, de modelos que funcionam satisfatoriamente... A
verdade maior: ainda conhecemos muito pouco – não raro, somos
surpreendidos com algumas “anomalias” de comportamento – e aí somos
instados a rever conceitos, formular novas relações funcionais, enfim,
conhecer melhor a lógica do sistema natural. Quando um modelo
supostamente “consolidado” deixa de oferecer uma resposta consistente
com a realidade, ou seja, quando a previsão não se confirma, não significa o
seu absoluto fracasso – isso até permite conhecer a abrangência e as
limitações do modelo. Afinal, não é a natureza que tem de se ajustar à
nossa limitada capacidade de compreensão; esta é que deve ser explorada
e aproveitada de forma permanente e contínua, para oferecer predições
confiáveis. Poucas respostas na ciência são definitivas. Sempre, diante de
um fenômeno, estaremos formulando perguntas. Basicamente, em
modelagem, uma se destaca: Quantas e quais são as variáveis
intervenientes mais relevantes? A rigor, é impossível listar todos os fatores
que participam ou que concorrem para uma certa ocorrência. Isso, porém,
não chega a ser um problema, tampouco motivo para desânimo. Importa,
efetivamente, identificar os fatores (as variáveis) mais significativos, os que
causam maior impacto na qualidade e na magnitude do fenômeno.
A incerteza é um conceito humano modernamente acrescentado aos
modelos. Em alguns casos, o máximo que conseguimos alcançar é um
indício da resposta mais provável, o que já é bastante satisfatório, haja vista
a multiplicidade de parâmetros e variáveis presentes. Os bons modelos já
procuram incorporar a estimativa (probabilística) de erro, atenuando o
pretenso caráter determinístico das predições.
Na ciência, e na física de modo particular, trabalhamos com princípios, leis,
modelos e teorias. Chamamos de lei a formulação a respeito de algum tipo
de regularidade da natureza. Freqüentemente, os termos lei e princípio são
empregados com a mesma acepção. Basicamente, leis (ou princípios) são
enunciados ou relacionamentos matemáticos que buscam descrever o
comportamento natural.
Não devemos olvidar que a física é uma construção humana, e se sujeita,
portanto, a todas as limitações da capacidade perceptiva do homem e dos
6

7. instrumentos colocados à sua disposição. Bastante oportuno, então, iniciar o
estudo da mecânica com uma idéia clara dos objetivos e das limitações da
ciência. Certeza é o que se persegue, poucas vezes o que se alcança.
Sistematização
A mecânica costuma ser dividida em duas áreas: a estática, que cuida das
condições de equilíbrio de um corpo em repouso ou em movimento sem
mudança de velocidade, e a dinâmica, destinada ao estudo dos movimentos
de corpos acelerados. A dinâmica compreende a cinemática, que se ocupa
dos aspectos geométricos do movimento, objetivando uma análise
meramente descritiva, e a cinética, voltada para a análise das forças
promotoras de mudanças na velocidade. Na prática, todas essas áreas se
comunicam amplamente e estão amparadas num mesmo conjunto de leis e
princípios. Um bom conhecimento da dinâmica pressupõe um bom
conhecimento da estática, e vice-versa.
Nas páginas seguintes, estaremos dando passos iniciais para a
compreensão dos movimentos (causas e efeitos, simulação e modelagem).
Ênfase é dada, neste trabalho, aos problemas. A teoria é apresentada de
forma resumida, contemplando apenas os tópicos essenciais. Algumas
questões são resolvidas logo após apresentação dos princípios e noções
gerais, para sedimentar a compreensão. As listas mais extensas de
problemas estão colocadas na última parte deste caderno e estão
separadas por tema.
Estas notas estão orientadas à dinâmica da partícula. Num módulo
subseqüente, será abordada a dinâmica dos corpos rígidos, sendo estes
tratados tridimensionalmente, compreendendo os movimentos translacionais
e rotacionais.
Mecânica clássica
A mecânica clássica, ou newtoniana, está fundamentada nas leis propostas
por Isaac Newton, no século XVII. Embora se tenha revelado inapta para
explicar todos os tipos e circunstâncias de movimento, notadamente aqueles
envolvendo massas ou velocidades imensas ou massas extremamente
baixas (partículas no mundo atômico), a mecânica clássica responde
satisfatoriamente aos casos mais comuns do nosso dia-a-dia, de massas e
7

8. velocidades moderadas. A sua evolução, como área do conhecimento, foi
viabilizada a partir de instrumentos de medição do tempo2.
Um breve histórico
Na mecânica clássica, três estudiosos se destacam. O primeiro deles,
Johannes Kepler (1540-1603), utilizando os dados coligidos por Tycho
Brahe, concebeu a primeira descrição matemática do movimento dos
planetas.
Galileu Galilei (1564-1642), com os experimentos utilizando pêndulos e
corpos em queda livre, foi um dos mais notáveis colaboradores para a
construção da moderna ciência, como criador do método experimental,
aliando a hipótese teórica à sua verificação por meio de experiências. Sua
principal obra, sobre o movimento dos corpos, foi publicada em 1634, sob o
título Discorsi e dimonstrazioni matematiche intorno a due nuove science.
Atribui-se, no entanto, a Isaac Newton (1642-1727) a contribuição mais
significativa para o amadurecimento dos princípios da dinâmica.
Sobre Newton
Isaac Newton nasceu na Inglaterra, em 1642, ano da morte de
Galileu Galilei. Diversos avanços na Física e na Matemática são
devidos a Newton: desenvolvimento do binômio de Newton,
criação e desenvolvimento do cálculo diferencial e integral, estudo
dos fenômenos ópticos, concepção das leis da mecânica clássica
e desenvolvimento das idéias acerca da gravitação. Sua principal
obra, Philosophiae Naturalis Principia Mathematica, foi publicada
em 1687 e o consagrou como um dos maiores gênios da história.
Interessante notar que a maior parte de sua obra foi desenvolvida
até os 24 anos de idade. Newton morreu em 1727, quando era
presidente da Real Academia de Ciências da Inglaterra, cargo que
vinha ocupando desde 1703. Até o início do século XX, toda a
Física era baseada e inspirada no trabalho de Newton. Suas
concepções, ainda hoje aplicáveis a um grande número de
fenômenos, foram reformuladas em 1905 por Albert Einstein, em
sua Teoria da Relatividade.
2
Pode-se afirmar que a estática, isoladamente, exibiu avanços bem antes de Newton, haja
vista prescindir da medição da variável tempo.
8

9. Dois avanços significativos, verdadeiramente revolucionários, foram
experimentados no século XX, com o advento da teoria quântica e da teoria
relativística.
O método científico
A formulação de princípios e leis, como fruto de observações sistemáticas e
verificações experimentais, deve seguir uma certa disciplina e metodologia,
logicamente concebida, de forma a se evitarem sofismas e leituras
inconsistentes dos fenômenos. Coube a Galileu, no século XVII, demonstrar
a importância das experiências e medidas precisas para a construção do
saber científico. Até então, era amplamente majoritária a idéia de que
somente o raciocínio filosófico e as concepções aprovadas pelos antigos
pensadores “permitiam” conhecer a verdade.
As duas características marcantes do novo método científico são a
experimentação e a matematização. Com efeito, a ciência só pode avaliar
adequadamente uma teoria se houver condições para a aplicação do
método científico.
Em síntese, o seguinte fluxo procedimental deve ser cumprido na aquisição
de verdade científica3.
3Nem sempre, o cumprimento desses passos leva a uma descoberta ou teoria científica. Em
algumas situações, chegamos a descoberta por acaso, quando estamos pesquisando outras
coisas. É o que se denomina serendipidade.
9

10. Grandezas físicas e medições
Qualquer entidade suscetível de medida é denominadadas grandezas é
significa comparar, cotejar. Em Física, a maioria
grandeza. Medir
dimensional, ou seja, ao seu valor deve estar associada uma unidade de
medida (padrão de referência). Há, porém, algumas grandezas que são
adimensionais, constituindo simples fatores de relacionamento entre outras
grandezas dotadas de dimensão.
Uma importante classificação das grandezas físicas refere-se ao nível de
informações necessárias para que ela esteja completamente caracterizada.
Assim, existem as grandezas escalares e as grandezas vetoriais4. Uma
grandeza escalar requer apenas uma valoração numérica denotando a sua
magnitude. São exemplos de grandezas escalares o tempo, a massa, o
comprimento. As grandezas vetoriais, por sua vez, são esclarecidas desde
que se conheçam a sua intensidade, o seu sentido e a sua direção. São
exemplos de grandezas vetoriais a força, a velocidade, a aceleração.
O sistema internacional de unidades
A existência de diversos padrões de medidas revelou-se inconveniente para
o intercâmbio tecnológico e comercial entre as nações. Motivações
econômicas e comerciais ensejaram a definição de um sistema de unidades
que fosse comum às diversas culturas e sociedades. Temos, hoje, um
conjunto de padrões de medidas amplamente aceito. Esse sistema (SI)5
resultou da XI Conferência Geral da Comissão Internacional de Pesos e
Medidas, realizada em Paris, no ano de 1960. O Brasil oficializou sua
adesão a esse sistema em 1963.
Alguns países desenvolvidos, como os Estados Unidos e a Inglaterra, por
exemplo, ainda nos dias atuais, empregam paralelamente unidades distintas
daquelas definidas no SI. Por isso, o usuário deve estar, portanto, sempre
atento aos fatores de conversão entre unidades. A tendência, no entanto, é
de que as unidades do SI se consagrem como efetivamente universais.
4
A entidade vetor, usada para retratar grandezas vetoriais, é apresentada no capítulo
seguinte. A breve noção de análise vetorial é também ali oferecida.
5 Originalmente, em francês: Système International d’Unités.
10

11. Em várias situações, dada a magnitude do que está sendo mensurado, é
conveniente a adoção de múltiplos (ou submúltiplos) de unidades básicas.
Nesse caso, geralmente são acrescentados prefixos gregos (por exemplo,
mega, quilo, mili, micro, etc.) ao nome da unidade, para compor uma nova
base de comparação.
Grandezas fundamentais
São consideradas fundamentais as seguintes grandezas: comprimento
(distância), tempo, massa, temperatura, intensidade de corrente elétrica,
intensidade luminosa. A partir dessas grandezas, todas as demais
grandezas físicas podem ser expressas.
As três primeiras são de especial interesse no estudo da mecânica. Suas
unidades no SI são, respectivamente, o metro (m), o segundo (s) e o
quilograma (kg), assim definidos:
metro: comprimento do trajeto percorrido pela luz no vácuo durante um intervalo de
tempo de 1/299 792 458 de segundo; o metro padrão é a distância entre duas linhas
paralelas existentes num protótipo de platina iridiada, depositada em Paris, na
temperatura de zero graus Celsius e em condições de sustentação perfeitamente
definidas.
segundo: duração de 9 192 631 770 vezes o período de determinada radiação
emitida, no seu estado fundamental, por um dos isótopos do césio (o nuclídeo césio
133).
quilograma: massa do protótipo internacional constituído por um cilindro de platina e
10% de irídio depositado no Bureau Internacional de Pesos e Medidas (Paris).
Análise dimensional
Adotam-se os seguintes símbolos para expressar a dimensionalidade das
grandezas físicas fundamentais:
Comprimento: L
Tempo: T
Massa: M
Temperatura:
Intensidade de corrente elétrica: I
Intensidade luminosa: Il
11

12. As grandezas apresentadas a seguir, com suas respectivas expressões
dimensionais, são algumas das que serão exploradas neste texto:
1
Velocidade: V L .T
2
Aceleração: A L .T
2
Força: F M . L .T
2 2
Energia: E M . L .T
2 3
Potência: P M . L .T
1
Quantidade de movimento: Q M . L .T
A análise dimensional constitui procedimento valioso para a verificação da
consistência de qualquer formulação matemática de uma grandeza física.
Pelo princípio da homogeneidade dimensional, “toda equação que traduz
um fenômeno físico verdadeiro é, necessariamente, homogênea do ponto-
de-vista dimensional”.
Além disso, de acordo com o teorema de Bridgman (ou de previsão de
fórmulas), “se experimentalmente constatado que uma grandeza física Y
depende apenas das grandezas físicas A, B, C,..., todas independentes
entre si, então X pode ser expresso como o produto de um fator puramente
numérico k por potências , , ,..., das grandezas das quais ele depende”.
Assim, podemos escrever, por exemplo:
X f ( A, B, C,...)
X k. A .B .C ...
Ordem de grandeza
Denominamos ordem de grandeza a potência de 10 mais próxima do valor
da grandeza. A identificação da ordem de grandeza é útil para efeitos
comparativos, além de permitir cálculos expeditos de razoável aproximação.
Alguns exemplos:
- O valor 18 está entre 10 e 100, mais próximo de 10 do que de 100. Logo, a sua
ordem de grandeza é 101.
12

13. - O valor 78 está entre 10 e 100, mais próximo de 100 do que de 10. Logo, a sua
ordem de grandeza é 102.
- O valor 0,0015 está entre 10-3 e 10-4, mais próximo de 10-3 do que de 10-4. Logo, a
sua ordem de grandeza é 10-3.
Notação científica
Com a notação científica, a exibição e a manipulação de valores (grandes
ou pequenos) se tornam mais simples, além de se constituir uma útil
uniformização nos diversos textos da literatura técnica. Isso porque permite
uma rápida comparação baseada na ordem de grandeza.
Nessa perspectiva, qualquer valor numérico deve ser escrito como o produto
de um número entre 1 e 10 por uma potência de base 10. Por exemplo, o
número 2300 seria expresso 2,3x103 (ou 2,3.103).
Algarismos significativos e precisão de medidas
Quando empregamos instrumentos para medir alguma grandeza, a
qualidade da resposta depende do nível de precisão e sensibilidade.
Sempre haverá algum erro (ou incerteza) embutido nessa mensuração.
Basicamente, podem ser destacados três tipos de erros: grosseiros,
sistemáticos ou acidentais. Os primeiros são detectáveis através de análise
uma linha tendencial de comportamento ou em razão de discrepâncias
acentuadas em relação ao esperado (valor médio); os erros sistemáticos,
via de regra, são atribuíveis à deficiência de calibração do aparelho de
medida (se percebidos a tempo, antes do processamento, os dados podem
até ser aproveitados, às vezes pela aplicação de um simples fator de ajuste
ou correção); os erros acidentais, por outro lado, podem ser produzidos por
descuido, negligência, imperícia ou imprudência do operador (daí a
necessidade de treinar bem (e valorizar) as pessoas responsáveis pelo
trabalho de coleta de dados, seja no campo, seja em laboratório).
Uma vez realizadas as medidas, uma dúvida freqüente é sobre quantos
algarismos decimais adotar. Convenciona-se, então, usar, no máximo, uma
casa decimal além da precisão do resultado (um algarismo incerto
duvidoso).
Consideremos, por exemplo, uma medição efetuada com uma régua escolar
de 30cm, em que estão indicadas graduações em centímetros e em
13

14. milímetros. Não é possível, por esse instrumento, alcançar precisão acima
dessa menor medida.
Denominam-se algarismos significativos de uma medida os algarismos
corretos e o primeiro algarismo duvidoso. Uma possível leitura com aquela
nossa régua seria 18,65cm, em que o 1, o 8 e o 6 são algarismos corretos e
o 5, algarismo duvidoso.
Não é razoável exibir-se mais de um algarismo duvidoso.
Para a contagem dos algarismos significativos, devemos observar que o
algarismo 0 (zero) somente assume esse caráter se estiver posicionado à
direita de outro algarismo significativo. Por exemplo, em 0,0053 temos
apenas dois algarismos significativos (o 5 e o 3), já que os zeros não são
significativos. Por outro lado, em 53000 temos cinco algarismos
significativos; pois, nesse caso, também os zeros são significativos.
Dúvidas surgem, com freqüência, quando se promove a conversão de unidades.
Nesse caso, a tendência (aos desavisados) é que apareçam 0 (zero) que não são
significativos. Por exemplo, poder-se-ia expressar 2,6m como 260cm, dando a
impressão de que o algarismo 6 assume, agora, caráter de algarismo correto, o que
é inconsistente. A notação científica é o expediente recomendado para se evitar tal
equívoco. Assim, de fato, 2,6m corresponde a 2,6.102cm; o algarismo 6 é duvidoso
na expressão em metros e assim continua sendo após a conversão de unidade.
Operações com algarismos significativos
Algumas regras básicas devem ser obedecidas nas operações com
algarismos significativos, a fim de não se introduzir uma falsa precisão aos
resultados de cálculo, já que também estes devem ser apresentados apenas
com os algarismos significativos.
i. No resultado das operações de multiplicação e divisão, o
número de algarismos significativos não deve ser superior ao
do de algarismos significativos do número operado de menor
precisão.
Se pretendemos multiplicar os valores 2,34 e 2,6, o resultado deve
ser expresso como 6,1 (ou seja, 6,084 arredondado para uma casa
decimal)
ii. No resultado das operações de adição e subtração, o número
de algarismos significativos não deve ir além da última casa
14

15. decimal ocupada por algarismos significativos em todos os
números operados. Portanto, ao somarmos (ou subtrairmos)
parcelas, devemos verificar qual dessas parcelas apresenta o
menor número de casas decimais, o que servirá de base para
o estabelecimento do número de dígitos do resultado. As
parcelas com número superior de casas decimais serão
convenientemente arredondas.
Seja, por exemplo, a operação soma das seguintes parcelas: 235,87,
82,465 e 0,8 com, respectivamente, duas, três e uma casas decimais
em suas expressões numéricas. O resultado conterá, então, uma
casa decimal. O arredondamento das duas primeiras parcelas
conduz a 235,9 e 82,5. Daí a soma total será 319,2cm.
As regras aqui apresentadas não são absolutas ou definitivas. Há, inclusive,
algumas divergências (não muito relevantes, porém) entre os autores mais
consagrados. Importa, efetivamente, que as operações com números
significativos sejam feitas com critérios razoáveis, não conferindo ao
resultado uma precisão que inexiste.
Oportuno observar, ainda, que valores de constantes presentes em
expressões matemáticas de leis físicas, quando não são resultados diretos
de medidas, não estão sujeitas à contagem de algarismos significativos,
para efeito de operações.
Aplicações:
Problemas resolvidos:
1) Efetuada a medição da distância entre duas cidades, encontrou-se o valor
38,5km. Comente por que não se deve escrever 38500m no lugar da leitura
original.
R.: No número 38,5 temos três algarismos significativos, sendo o 5 algarismo
duvidoso, o que é compatível com o instrumento utilizado na medição. Se
passássemos a expressar a distância pelo número 38500, embora preservando a
lógica da conversão da unidade (já que 1km equivale a 1000m), estaríamos
ampliando o número de algarismos significativos e “transformando” o algarismo
duvidoso 5 em algarismo correto. Note que em 38500 temos cinco algarismos
significativos, sendo o zero mais à direita o “suposto” duvidoso.
15

16. 2) Considere uma experiência para a medição de velocidade, utilizando um
instrumento que oferece 1% de precisão na medida de distância. Observa-
se que uma partícula se desloca vinte centímetros em seis segundos.
Expresse a velocidade.
R.: Calculando a razão entre a distância percorrida e o intervalo de tempo
correspondente, encontramos:
v 3,33...cm / s
A forma de apresentação acima é inadequada. Com efeito, devemos adotar, no
máximo, uma casa decimal além da precisão do resultado. Desse modo, se a
distância é medida com 1% de precisão, temos:
v 3,33 0,03cm / s
Assim, o valor verdadeiro da velocidade está entre 3,30cm/s e 3,36cm/s. Os dois
primeiros dígitos são corretos; o terceiro, duvidoso.
16

17. Elementos de análise vetorial
D efine-se vetor6 como uma entidade matemática dotada de módulo,
direção e sentido. A designação, criada por Willian Hamilton (1805-
1865), deriva do latim e significa transportador. Sua representação
geométrica é feita por um segmento de reta, cujo comprimento corresponde
ao módulo, e uma seta numa das extremidades indicando o sentido da
grandeza que está sendo retratada. Uma importante característica do vetor
é que ele não tem uma posição fixa no espaço; assim, a sua simples
translação (mudança de posição paralelamente a si próprio) não o altera, ou
seja, um mesmo vetor pode ser apresentado em diferentes posições no
espaço e em diferentes sistemas de coordenadas.
Na figura seguinte, as três setas estão representando um mesmo vetor.
A notação vetorial adotada neste texto consiste numa letra com seta

encimada (ex.: a ). Alguns autores preferem apresentar a letra em negrito,
sem a seta (ex.: a). O módulo (comprimento ou intensidade) desse vetor é

denotado por a ou simplesmente a.
Há diversas operações matemáticas das quais vetores participam: eles
podem ser somados, subtraídos ou multiplicados. Não se admite, porém, a
divisão de um vetor por outro vetor. A operação adição (soma ou subtração)
requer que as grandezas envolvidas sejam de mesma natureza (somente
vetor pode ser somado a vetor; somente escalar pode ser somado a
escalar). Subtrair um vetor de outro significa somar a este o oposto daquele.
A multiplicação, por outro lado, consegue associar um vetor a um escalar;
6 A concepção da entidade vetor é posterior ao surgimento da Mecânica Newtoniana,
somente se consolidando no final do século XIX.
17

18. neste caso, o produto de um escalar por um vetor resulta num vetor cujos
módulo e sentido podem ser alterados, porém nunca a direção. O produto
de dois vetores traz como resultado um escalar ou um vetor, conforme a
maneira como se procede: no primeiro caso, também chamado de produto
interno, obtém-se um valor (positivo, negativo ou nulo), enquanto no
segundo, dito produto vetorial, a resposta é um vetor cuja direção é
perpendicular ao plano definido pelos dois vetores que estão sendo
multiplicados.
Vetores unitários
Tanto no sistema cartesiano (retangular) de coordenadas, quanto no
sistema normal-tangencial ou no sistema radial-transversal, podemos definir
vetores unitários em cada direção principal do sistema, o que permite
expressar qualquer outro vetor como combinação linear desses vetores
unitários.
18

19. Notação vetorial cartesiana
Num sistema cartesiano tridimensional, os vetores podem ser expressos em
termos de sua projeção em cada um dos eixos perpendiculares x, y e z.
Assim, por exemplo:
   
a a x .i a y . j a z .k
   
b bx .i by . j bz .k
Soma de vetores
Há diversos processos metodológicos para efetuar a soma (ou subtração)
de vetores. A mais simples, se trabalhamos com a notação vetorial
cartesiana, consiste em adicionar algebricamente as projeções dos vetores
relativas a cada um dos três eixos perpendiculares, associando a soma ao
respectivo vetor unitário, como mostrado a seguir:
19

20.        
a b a x .i a y . j a z .k bx .i by . j bz .k
    
a b (a x bx ).i (a y by ). j (a z bz ).k
Produto escalar de vetores
 
O produto escalar, ou produto interno, dos vetores a e b é o valor
(escalar) obtido por
   
a b a .b . cos
onde o ângulo entre os dois vetores (0 180 ).
Decorre da definição que:
  
i .i 1 j. j 1 k .k 1
  
i.j 0 i .k 0 k. j 0
Portanto:
      
a.b (a x .i a y . j a z .k ).(bx .i by . j bz .k )

a.b a x .bx a y .by a z .bz
   
Observa-se, facilmente, que a b b a , ou seja, o produto escalar é
comutativo.
Na multiplicação de escalar por vetor, vale a propriedade:
     
m.( a.b ) (m.a ).b a.( m.b ) (a.b ).m
O produto escalar goza, ainda, da propriedade distributiva. Significa dizer:
      
a (b c) a b a c
20

21. A operação produto escalar de vetores é importante, por exemplo, para a
definição da grandeza física trabalho, como será visto adiante.
Produto vetorial
O resultado do produto vetorial (ou produto externo) é um vetor
perpendicular ao plano definido pelos dois vetores que estão sendo
multiplicados.
Para identificar a orientação do vetor resultante do produto vetorial, aplica-
se a “regra da mão-direita”.
O módulo do produto vetorial é dado por:
   
a b a . b .sen
 
sendo o ângulo formado entre os vetores a e b (0 180 ).
21

22.   
i j k
 
a b ax ay az
bx by bz
    
a b (a y .bz a z .by ).i (a z .bx a x .bz ). j (a x .by a y .bx ).k
A operação produto vetorial (ou externo) é importante, por exemplo, para o
estabelecimento da grandeza momento angular.
Decorre da definição que:
     
i i 0 j j 0 k k 0
        
i j k j k i k i j
        
i k j j i k k j i
No produto vetorial, vale a propriedade distributiva:
      
a (b c ) a b a c
Por outro lado, é inaplicável a propriedade comutativa. Ou seja:
   
a b b a
   
Porém, com efeito: a b b a
Na multiplicação por um escalar, vale a propriedade:
       
m.( a b ) (m.a ) b a (m.b ) (a b ).m
Lei dos cossenos
  
Sejam os vetores a , b e c , mostrados na figura seguinte.
22

23. Temos as seguintes relações:
  
c a b
  
a c b
Pode ser demonstrado que
2 2 2  
c a b 2. a . b . cos
Lei dos senos
Seja o triângulo dos lados a, b e c , da figura seguinte.
Vale a relação:
a b c
sen sen sen
Derivação e integração de funções vetoriais
- As expressões seguintes são válidas, desde que as funções a(t) e b(t)
sejam suaves e contínuas para todo t.
   
d (a b ) da d b
dt dt dt
   
(a b )dt a.dt b.dt
   

d (a b ) da  db
b a
dt dt dt
   
da b da   db
b a
dt dt dt
23

24. Aplicações:
Problemas resolvidos:
1) Um veículo se desloca 10km na direção nordeste, em seguida 5km na
direção norte, em seguida 15km para leste, em seguida 30km na direção
noroeste, onde pára. Localize esse veículo, após todos os percursos, em
relação a seu ponto de partida.
R.: Consideremos (0,0) as
coordenadas do ponto de partida, o
norte coincidindo com a orientação
positiva de y e o leste, com a
orientação positiva de x.
A posição final do veículo, após os quatro deslocamentos mencionados, é obtida
por:
      
r 5. 2i 5. 2 j 5. j 15 .i 15 . 2 .i 15 . 2 j
  
r 5.(3 2. 2 ).i 5.(1 4. 2 ) j
   
2) Em geral, a b a b . Comente.
R.: O módulo da soma de dois vetores equivale à soma dos módulos desses dois
vetores somente quando o ângulo formado entre eles é nulo. Ou seja, apresentam
ambos a mesma direção e o mesmo sentido. Isso é previsto na lei dos cossenos
(basta lembrar que esta função trigonométrica assume valores no intervalo
1; 1 ).
Portanto, pode-se afirmar que o módulo da soma de dois vetores está situado no
intervalo:
     
a b a b a b
O limite inferior desse intervalo corresponde à situação em que os dois vetores
apresentam a mesma direção, porém sentidos contrários.
24

25.   
3) Considere o vetor c perpendicular a cada um dos vetores a e b .
  
Mostre que c é também perpendicular a m.a n.b , para quaisquer
escalares m e n.
 
R.: Com base no produto vetorial: sec e a são perpendiculares, então
   
c a c .a
 
Similarmente, se c e b são perpendiculares, então
   
c b c .b
  
Fazendo, agora, o produto vetorial de c e m.a n.b e reconhecendo a
distributividade dessa operação, temos:
      
c (m.a n.b ) c (m.a ) c (n.b )
      
c (m.a n.b ) m.( c a ) n.( c b )
      
c (m.a n.b ) m. c . a n. c . b
     
c (m.a n.b ) c (m. a n. b )
  
Seja o ângulo formado entre c e m.a n.b . Temos, então, que:
  
c.(m.a n.b )
sen    1
c . m.a n.b
Daí, 900
  
Portanto, c e m.a n.b são perpendiculares.
     
4) Considere os vetores a .i 6. j e b 3.i 2. j
perpendiculares. Determine o valor de .
 
R.: Sendo perpendiculares a e b , temos que o produto escalar desses vetores é
nulo. Assim:
 
a b 0
.3 ( 6).2 0
Daí: 4
25

26.    
5) Determine o ângulo formado entre os vetores a 2.i 6. j k e
   
b 4.i 3. j 2.k .
R.: O ângulo entre dois vetores pode ser determinado com base o seu produto
escalar, conhecida a relação:
   
a b a .b . cos
Substituindo os valores:
 
a b 2.4 ( 6). 3 1.( 2) 12

a 22 ( 6) 2 12 41

b 42 32 ( 2) 2 29
 
a b
cos  
a .b
12
cos
41. 29
arccos 0,348
  
6) Três vetores a , b e c , mutuamente perpendiculares e não nulos no
   
espaço, são combinados produzindo o vetor d .a .b .c ( ,
e são escalares). Encontre as expressões para , e
   
(componentes do vetor d relativas ao sistema de referência a , b , c ).
  
R.: Sendo os vetores a , b e c mutuamente perpendiculares, temos que:
   
a b a b cos90 0
   
a c a c cos90 0
   
b c b c cos90 0
 
Se multiplicarmos escalarmente os vetores a e d :
     
a d a ( .a .b .c )
Aplicando a propriedade distributiva:
26

27.      
a d .a.a .a.b .a.c .a.a
 
a d
Então:   (Note-se que aqui não estamos dividindo vetor por vetor (o
a a
que não é possível), mas escalar por escalar).
De modo semelhante, chegamos a:
   
b d c d
  e  
b b c c
27

28. Conceitos fundamentais da mecânica
D iversos conceitos e abstrações teóricas são incorporados nos textos de
Mecânica. No desenvolvimento dos capítulos, estaremos definindo
grandezas físicas e estabelecendo os seus relacionamentos através de leis.
Preliminarmente, porém, cabe apresentar os elementos básicos que
permearão toda a abordagem da Mecânica Clássica.
Partícula
A entidade partícula constitui uma abstração da Física, bastante utilizada na
Mecânica, para indicar que o móvel é pequeno e suas dimensões
geométricas são irrelevantes no cenário em que se desenvolve o fenômeno.
Uma partícula (ou ponto material) apresenta uma certa quantidade de
matéria, isto é, tem massa, porém são desprezíveis a sua forma e o seu
tamanho. Esse conceito é aplicável a objetos cujas dimensões,
relativamente às demais grandezas espaciais envolvidas, não afetam a
análise do movimento.
Portanto, quando mencionamos partícula, queremos dizer que não estamos
considerando as dimensões reais do corpo que se desloca e, dessa forma,
a abordagem se limita ao movimento de translação. Evidentemente, apesar
da abstração de tamanho, a ela atribuímos, paradoxalmente, uma massa;
aceita-se que toda a matéria esteja concentrada em seu centro de massa e
a descrição translacional desse ponto central seja suficiente para os
objetivos da análise.
Aspectos relativos à rotação e deformação não são considerados para a
partícula material. Por outro lado, se um objeto apresenta apenas
movimento de translação, ele pode ser tratado como partícula, já que todos
os seus pontos se deslocam igualmente.
Tempo
Newton, em seu tratado “Os Princípios Matemáticos da Filosofia Natural”,
introduziu o conceito de tempo absoluto. Segundo ele, “o tempo absoluto,
verdadeiro e matemático, por si só e por sua própria natureza, flui
uniformemente, não mantendo relação com qualquer coisa externa.” Assim,
o tempo não estaria sujeito a condição física alguma.
A concepção de tempo, tal como proposta por Newton, embora prevaleça no
âmbito da mecânica clássica, deve ser revista para acomodar as
28

29. circunstâncias de velocidades muito altas (comparáveis à da luz) ou de
campos gravitacionais muito intensos. Isso significa que podemos “aceitar” o
tempo absoluto somente quando as velocidades e os campos gravitacionais
forem relativamente baixos, que serão, enfim, os casos discutidos neste
texto.
O conceito mais moderno de tempo relativo (que pode se dilatar,
dependendo do observador) pode ser extraído da leitura de textos da
mecânica relativística, desenvolvida a partir do início do século XX.
Espaço
O espaço é o palco de acontecimento dos fenômenos físicos. Costuma-se
atribuir a ele um caráter tridimensional, ou seja, de certa volumetria. No
entanto, em condições particulares, a análise pode ser conduzida
satisfatoriamente reduzindo-o a duas dimensões (por exemplo, no
movimento de uma partícula ao longo de uma trajetória plana) ou a uma
dimensão (por exemplo, no movimento de uma partícula ao longo de uma
trajetória retilínea).
Referencial
A necessidade de estabelecimento de referencial decorre do caráter não
absoluto dos fenômenos naturais, notadamente aqueles relacionados ao
movimento. Dependendo da perspectiva, um mesmo fato pode ensejar
diferentes leituras e interpretações. Por isso, as leis da Física devem ser
aplicadas somente após a clara definição de quem está observando o
fenômeno. Via de regra, o referencial deve ser assumido como um sistema
rígido. Em relação a este, são especificadas as coordenadas espaciais e
temporais de eventos físicos.
É a partir da caracterização do referencial que a análise do comportamento
da partícula (ou sistema de partículas) pode ser conduzida, bem assim
qualquer inferência sobre o seu repouso ou movimento.
No âmbito da mecânica, os sistemas de referência podem ser classificados
em inerciais ou não-inerciais, de acordo com a sua mobilidade em relação a
um ponto fixo distante.
Movimento
Não é possível qualquer alusão a movimento sem que previamente seja
definido um referencial. De fato, o fenômeno movimento consiste,
29

30. essencialmente, na variação, em função do tempo, das coordenadas de
localização de um corpo em relação a algum sistema de referência.
Portanto, não é razoável a afirmação de que algo se movimenta quando
muda de posição. Tal assertiva é frágil, incompleta e merece reparos.
Dentro de um veículo que trafega numa estrada, as pessoas estão em
movimento em relação a um poste fincado à margem da rodovia; porém,
dois passageiros no interior desse veículo encontram-se parados um em
relação ao outro, ainda que ambos estejam se movimentando em relação ao
poste aludido. Também não se pode afirmar que um marco na estrada
esteja imóvel: ele se movimenta, sim, se tomado o veículo como referência.
Força
Todos temos uma idéia (ou conceito intuitivo) do que seja força e do que ela
é capaz. Na verdade, a força constitui mais uma entidade (grandeza)
concebida para o estabelecimento de relações dinâmicas. Sua efetiva
mensuração somente é possível a partir dos efeitos que ela produz.
Adiante, quando forem apresentadas as leis de Newton do movimento,
veremos que uma razoável definição de força é: todo agente capaz de
alterar o módulo ou a direção da velocidade de um corpo; todo agente capaz
de atribuir uma aceleração a um corpo. Por outro lado, a força pode ensejar
diversos outros processos além de movimentos acelerados.
Energia
Como clássica definição, temos a energia como a propriedade de um
sistema que lhe permite realizar trabalho. A energia pode se apresentar sob
várias formas (potencial, cinética, calorífica, elétrica, eletromagnética,
potencial, química, radiante etc.), transformáveis umas nas outras, e cada
uma capaz de provocar fenômenos bem determinados e característicos nos
sistemas físicos.
É justo asseverar que essa foi, até hoje, uma das mais brilhantes
concepções da ciência, em razão, sobretudo, do caráter intercambiável e de
sua absoluta indestrutibilidade.
Em todas as transformações de energia há completa conservação em sua
quantidade (a energia não pode ser criada, nem destruída, mas apenas
transformada). Até mesmo a massa de um corpo pode-se transformar em
30

31. energia; por outro lado, energia sob forma radiante pode transformar-se em
um corpúsculo com massa, como demonstrado pela Física Moderna.
Particularmente, a energia dita mecânica se apresenta sob a forma potencial
(gravitacional, elástica etc.) ou cinética (translacional, rotacional etc.). É da
energia mecânica que nos ocuparemos mais neste texto. Adiante, será
comentado o princípio da conservação da energia, enfatizando como o
conceito de energia pode ser proveitoso na análise e solução de variados
problemas de mecânica.
31

32. Cinemática da partícula
B asicamente, quatro variáveis estão presentes nas equações
cinemáticas: a aceleração (a), a velocidade (v), a posição (s) e o tempo
(t). Em geral, o tempo se comporta como variável independente, a partir da
qual as demais são estabelecidas e/ou identificadas. Sendo conhecida uma
relação entre duas dessas variáveis, uma terceira pode ser alcançada
utilizando-se as equações exibidas adiante.
Cinemática da partícula
Primariamente, é o deslocamento a grandeza apta a indicar a ocorrência de
movimento. Um corpo (ou partícula) se desloca quando há uma mudança
em sua posição. Esse fenômeno, evidentemente, se desenvolve num certo
intervalo de tempo; da relação entre o deslocamento e o tempo obtém-se a
velocidade.
Assim:

 r
v méd
t
Sendo infinitesimal o intervalo de tempo em que ocorre um certo
deslocamento também infinitesimal, temos a velocidade instantânea (ou
simplesmente velocidade).

 r
v limt 0 t

 dr
v
dt
Ou seja, a velocidade (grandeza vetorial) é a derivada da posição no tempo,
significando a taxa de variação temporal do deslocamento.
Também necessária à descrição do movimento é a taxa de variação
temporal da velocidade, grandeza (vetorial) que denominamos aceleração.
Assim:

 v
a méd
t
32

33. Sendo infinitesimal o intervalo de tempo em que se verifica a variação,
também infinitesimal, da velocidade, temos a aceleração instantânea (ou
simplesmente aceleração).

 v
a lim
t 0 t

 dv
a
dt
Em algumas situações, é possível e conveniente relaxar o caráter vetorial da
velocidade, omitindo-se a exata caracterização da sua direção.
Esclarecendo: se a trajetória (caminho ou configuração de percurso) é
satisfatoriamente conhecida, se a posição está identificada ao longo dessa
trajetória (como ocorre, por exemplo, numa rodovia), é bastante aceitável
enfocar a velocidade sem os seus elementos de grandeza vetorial,
porquanto implícitos. Nesse caso, podemos operar com uma nova
grandeza, denominada velocidade escalar, a qual pode assumir valor
positivo ou negativo, de acordo com a orientação de crescimento dos
marcos posicionais. Com efeito, a orientação da grandeza, inerente a seu
caráter vetorial, passa a ser transferida para a trajetória, sem qualquer
prejuízo para a análise.
Nas figuras seguintes, a trajetória (eixo x) está orientada da esquerda para a direita.
O ponto P, à direita do marco posicional 0, assume uma posição escalar positiva. O
ponto P’, à esquerda do marco posicional 0, assume, por outro lado, posição
escalar negativa.
Admitindo-se que, após um intervalo de tempo t, a partícula se desloca x,
temos a velocidade escalar média:
33

34. x
v méd
t
A velocidade escalar propriamente dita (ou instantânea) se expressa por:
dx
v
dt
Vale, assim, a seguinte convenção para o sinal da velocidade escalar:
positivo, quando o móvel (partícula) se desloca no sentido dos marcos
posicionais crescentes; negativo, quanto o móvel (partícula) se desloca no
sentido dos marcos posicionais decrescentes.
A aceleração, por sua vez, traduz o comportamento temporal da velocidade,
sendo, matematicamente, a derivada da velocidade em relação ao tempo
(variável independente). Como aludido anteriormente, trata-se de uma
grandeza vetorial; no entanto, em algumas situações, é viável a sua
apresentação sob a forma escalar, isto é, como um valor ao qual se associa
um sinal. Neste caso, o sinal (positivo ou negativo) não se refere
diretamente à variação da velocidade, em valor absoluto7. Deve ser
observado que uma aceleração positiva não significa, necessariamente,
aumento da velocidade.
7O sinal da aceleração escalar, assim como o da velocidade escalar, depende da orientação
estabelecida para o eixo de referência.
34

35. dv
a
dt
O esquema seguinte esclarece o significado da aceleração escalar positiva
e da aceleração escalar negativa.
Conhecido o comportamento temporal da posição, isto é, s f (t ) , a
aceleração pode ser obtida por:
d 2s
a
dt 2
Ou seja, a segunda derivada da posição em relação ao tempo.
Portanto, a aceleração, a posição e a velocidade assim se relacionam:
a.ds v.dv
As equações apresentadas até aqui são gerais e, portanto, aplicáveis a
qualquer tipo de movimento.
35

36. Particularmente, para o movimento que se desenvolve numa trajetória retilínea
conhecida, podemos tecer os seguintes comentários:
1. A direção da trajetória não muda durante o movimento;
2. A direção da velocidade e a direção da aceleração coincidem com a
da trajetória;
3. O módulo de deslocamento corresponde à diferença (em valor
absoluto) dos marcos posicionais;
4. A velocidade escalar e a aceleração escalar podem substituir, sem
prejuízo da análise cinemática, as grandezas vetoriais velocidade e
aceleração.
Velocidade média e velocidade média de percurso
A velocidade média de percurso ( v mp ) é definida em função da distância
total percorrida, sendo, portanto, uma grandeza escalar positiva. Essa
grandeza não deve ser confundida com a velocidade média ( v méd ), a qual
está associada ao deslocamento ou, mais propriamente, à mudança
posicional. Assim, a velocidade média de percurso é a relação entre a
distância total percorrida e o tempo demandado nesse percurso; a
velocidade média é a razão entre a mudança de posição e o tempo. Note-se
que a velocidade média pode assumir valor positivo ou negativo.
t2
v.dt
s t1
Assim: v méd
t t2 t1
sT
v mp
t
Na prática, a diferença entre esses dois conceitos se evidencia quando
ocorre mudança na direção da velocidade (ou seja, quando a velocidade
escalar muda de sinal).
Podemos estabelecer o seguinte algoritmo para o cálculo da velocidade
média de percurso:
36

37. 1. Identificar os instantes em que ocorrem mudanças no sinal da velocidade
escalar (quando o movimento muda de sentido);
2. Discretizar o intervalo de tempo de análise em subintervalos, definidos
entre duas mudanças sucessivas de sinal;
3. Calcular a variação posicional s (os espaços percorridos, em valor
absoluto), em cada subintervalo;
4. Determinar a razão entre o espaço total percorrido (soma dos s) e o
intervalo de tempo de análise.
Aplicações:
Problemas resolvidos:
1) Um veículo numa estrada retilínea percorre 15km a 50km/h mais 10km a
60km/h mais 5km a 75km/h. Determine a média aritmética das velocidades
e a velocidade média de seu percurso.
R.: Determinemos, inicialmente, o tempo demandado em cada etapa do percurso.
Para percorrer os primeiros 15km foram gastos 18 min; nos 10km seguintes, mais
10min e, nos 5km restantes, mais 4min. Assim, o trecho total de 30km foi
desenvolvido num intervalo de tempo total de 22min. Isso permite que a velocidade
média seja estimada em:
15 10 5
vm 0,94km / min 56,25km / h
18 10 4
A média aritmética das velocidades vale:
50 60 75
v 61,67km / h
3
Somente no caso do movimento uniformemente variado é que a média das
velocidades equivale à velocidade média.
2) Ao longo de uma trajetória plana horizontal, uma partícula se movimenta,
sendo a sua velocidade expressa por v (2.t 2 8.t ) m/s, com o tempo t
em segundos. Determine a velocidade média e a velocidade média de
percurso, no intervalo de tempo de 0 a 5s.
R.: Calculemos o deslocamento (medido ao longo da trajetória).
ds v.dt
5 5
s v.dt (2.t 2 8.t )
0 0
37

38. 5
2.t 3 5
s 4.t 2 16,67m
3 0
0
Podemos, então, calcular a velocidade média:
s 16,67
vméd 3,33m / s
t 5
Calculemos a distância total percorrida. Devemos, antes, identificar o(s) instante(s)
em que a partícula inverte o sentido de seu movimento. Isso ocorre quando a
2
velocidade se anula, ou seja, no instante t 4s (obtido de 0 2.t 8.t ).
De 0 a 4s, o móvel percorre 21,33m; de 4s a 5s, o percurso é de 4,67m. Portanto,
de 0 a 5s, o percurso total corresponde a 26,00m. Então, podemos calcular a
velocidade média de percurso:
sT 26,00
v mp 5,20m / s
t 5
O caso particular de movimento com velocidade constante (v)
Quando o valor da velocidade não se altera durante o movimento, este é
dito uniforme, independentemente da configuração da trajetória.
s v
ds v.dt
s0 0
s s0 v.t
s s0 v.t
A expressão acima representa a função horária da posição. O fato de o
movimento se desenvolver com velocidade de módulo constante não
implica, rigorosamente, a ausência de aceleração, como veremos mais
adiante.
Verifica-se, com efeito, que o único movimento possível na natureza
completamente destituído de aceleração é o movimento retilíneo uniforme
(MRU).
38

39. O caso particular de movimento com aceleração constante (a)
O movimento que ocorre com aceleração de módulo constante é
denominado movimento uniformemente variado (MUV). Exemplo desse
movimento ocorre quando um corpo cai livremente (queda livre) no vácuo,
onde a resistência do ar inexiste. Também próximo à superfície da Terra, o
movimento de queda de um corpo pode, em muitos casos, ser considerado
de aceleração constante.
A velocidade em função do tempo:
v t
dv a.dt
v0 0
v v0 a.t
A expressão acima é dita função horária da velocidade no MUV.
A posição em função do tempo:
s t
ds (v 0 a.t ).dt
s0 0
1 2
s s0 v0 .t .a.t
2
A expressão acima é dita função horária da posição no MUV.
A velocidade em função da posição:
v s
v.dv a.ds
v0 s0
v2 2
v0 2.a.( s s0 )
Esta equação é conhecida como Equação de Torricelli.
Note-se que as três últimas expressões apresentadas são aplicáveis tanto
ao movimento uniforme quanto ao movimento uniformemente variado. De
fato, o que caracteriza o MUV é a constância do valor da aceleração,
39

40. inclusive quando esta é nula (caso de MU). Ampliando esse raciocínio, as
equações de movimento variado são, com efeito, uma generalização desses
casos particulares.
Análise do movimento
Para a aplicação das equações precedentes, é necessário que se
estabeleça um sistema de coordenadas. No caso particular de trajetória
retilínea, é suficiente que seja especificada uma coordenada de posição ao
longo do percurso, com a identificação de uma origem fixa e a sua
orientação positiva. Também nesse caso, bastam escalares algébricos de
posição, velocidade e aceleração; os sinais algébricos indicarão os sentidos
das variáveis, na manipulação analítica das formulações matemáticas.
Classificação dos movimentos
Quanto à orientação da mudança de posição e da velocidade, os
movimentos podem ser classificados em:
Progressivo: o móvel assume posições cada vez mais elevadas,
considerando os marcos do sistema de referência. Nesse caso, costuma-se
dizer que a velocidade é positiva.
Retrógrado: o móvel assume posições cada vez mais baixas, considerando
os marcos do sistema de referência. Nesse caso, costuma-se dizer que a
velocidade é negativa.
Acelerado: o módulo da velocidade cresce com o tempo. Nesse caso o sinal
(positivo ou negativo) da aceleração deve coincidir com o da velocidade.
Retardado: o módulo da velocidade decresce com o tempo. Nesse caso os
sinais (positivo ou negativo) da aceleração e da velocidade devem ser
contrários.
Podemos encontrar as seguintes associações:
v 0 v 0
movimento acelerado e progressivo movimento retardado e progressivo
a 0 a 0
v 0 v 0
movimento acelerado e retrógrado movimento retardado e retrógrado
a 0 a 0
40

41. Interpretação de gráficos do movimento
Gráficos cartesianos são instrumentos bastante úteis para a representação
do movimento. Grande quantidade de dados pode ser retratada num gráfico.
Em geral, a sua confecção não envolve maiores dificuldades. Importa, para
o leitor, desenvolver habilidade na sua interpretação, explorando-os em
todos os seus pormenores.
A seguir, apresentamos alguns aspectos relevantes da leitura de gráficos
que relacionam as grandezas da cinemática.
A inclinação da reta tangente à curva num dado instante de tempo t
corresponde à grandeza definida pela derivada da grandeza exibida no eixo
das ordenadas em relação ao tempo. Ou seja, no gráfico posição versus
tempo, a inclinação traduz a velocidade; no gráfico velocidade versus
tempo, a inclinação traduz a aceleração, como mostra a figura seguinte.
41

42. Conhecido o gráfico posição versus tempo, podemos confeccionar o gráfico
velocidade versus tempo.
Conhecido o gráfico velocidade versus tempo, podemos confeccionar o
gráfico aceleração versus tempo.
42

43. A área sob a curva no gráfico
aceleração versus tempo
permite inferir a variação da
velocidade entre os limites do
intervalo de tempo considerado,
ou seja, de t1 a t2.
A área sob a curva no gráfico
velocidade versus tempo
permite inferir a variação
posicional da partícula entre os
limites do intervalo de tempo
considerado, ou seja, de t1 a t2.
43

44. Aplicações:
Problemas resolvidos:
1) Uma partícula de desloca da origem e ao longo de um eixo retilíneo. O
gráfico temporal da velocidade é apresentado na figura seguinte.
Represente em gráfico o comportamento temporal da posição e da
aceleração dessa partícula. Determine o instante em que a partícula volta a
passar pela origem.
R.: Podemos depreender do gráfico: i) no intervalo de 0 a 4s, o movimento é
uniformemente variado, ou seja, com aceleração constante igual a 1,5m/s2; ii) de 8s
a 12s, a aceleração constante vale -6m/s2; iii) no instante 10s, a velocidade é nula
(a partícula momentaneamente pára); iv) a partir de 12s, a velocidade é constante
igual -12m/s (aceleração nula).
Graficamente:
44

45. A partícula volta a passar pela origem quando a área sob a curva (considerada
grandeza escalar) for nula. Enquanto a velocidade é positiva, de 0 a 10s, a partícula
percorre 60m. Então, basta determinar, a partir de 10s, o instante correspondente a
uma área (no gráfico) de -60m. Pelo gráfico posição versus tempo, verifica-se que
isso ocorre no instante 16s.
2) Um estudante, pretendendo medir a aceleração da gravidade, resolve
fazer o seguinte experimento: num tubo evacuado, lança verticalmente para
cima uma bolinha, e mede, com precisão, os instantes de passagem, na
subida e na descida, dessa bolinha por um certo ponto do tubo. Esclareça a
lógica desse procedimento e apresente a expressão que fornece o valor de
g.
R.: Sejam t1 e t2 os instantes de tempo, ambos medidos
a partir do lançamento. No instante t1, a bolinha passa,
em movimento ascendente, pelo ponto de controle
(indicado na figura seguinte); no instante t2, a mesma
bolinha passa novamente por esse ponto de controle,
porém, agora, em movimento descendente.
No intervalo de tempo compreendido entre t1 e t2, o seu
percurso terá sido 2.h, onde h representa a altura
máxima alcançada a partir do ponto de controle.
Estando o corpo em movimento vertical no vácuo, sua aceleração equivale à da
gravidade (movimento de queda livre). No ápice de sua trajetória, a velocidade é
nula e o deslocamento da bolinha muda de sentido. Podemos, então, escrever:
1
2.h y0 vo .(t 2 t1 ) .g.(t 2 t1 ) 2
2
2.h vo .(t 2 t1 )
g
1
.(t 2 t1 ) 2
2
v o : velocidade na passagem pelo ponto de controle
Lembrando que: vo 2.g.h (da equação de Torricelli), temos:
45

46. 1
yo .g.t12
1 2
yo vo .t1 .g.t12 , daí: vo
2 t1
1 2
yo .g.t 2
1 2 2
yo vo .t 2 .g.t 2 , daí: vo
2 t2
Então:
yo g .t1 yo g .t 2
t1 2 t2 2
1 1 t2 t1
yo . g.
t1 t2 2 2
2. y o
Portanto: g
t1 .t 2

O sinal negativo indica que a aceleração da gravidade g está orientada

contrariamente ao sentido estabelecido para o eixo y, ou seja, o vetor g é vertical
e para baixo.
3) Uma partícula percorre uma trajetória retilínea, sendo que, em qualquer
instante, a posição, a velocidade e a aceleração apresentam valores
numericamente iguais. Apresente as funções horárias de posição e de
velocidade.
R.: Temos as seguintes relações:
dx v.dt dv a.dt
x t
dx
dt Sendo v numericamente igual a x:
xo
v to
x t
ln x x tt x (t ) x o .e t to
o o
Por outro lado:
46

47. v t
dv
dt Sendo a numericamente igual a v:
vo
a to
v t
ln v v tt v(t ) vo .e t to
o o
Movimento curvilíneo
No caso mais geral do movimento, a trajetória é descrita em três dimensões.
Um sistema cartesiano de coordenadas retangulares pode ser novamente
empregado para a análise.
As grandezas envolvidas são tratadas em termos de três componentes
mutuamente perpendiculares, segundo os eixos x, y e z.
Assim, o vetor posição se apresenta como:
   
r x.i y. j z.k
O módulo do vetor posição será:
r x2 y2 z2
47

48. A velocidade se expressa por:
   
v v x .i v y . j v z .k
dx dy dz
vx vy vz
dt dt dt
O módulo da velocidade será:
2 2 2
v vx yy zz
A aceleração ser expressa por:
   
a a x .i a y . j a z .k
dv x dv y dv z
ax ay az
dt dt dt
O módulo da aceleração será:
2 2 2
a ax ay az
Nota:
Denomina-se hodógrafo do movimento a curva descrita pela extremidade do vetor

velocidade v .
48

49. Independência das velocidades
A independência de dois movimentos simultâneos e perpendiculares foi
experimentalmente reconhecida por Galileu.
Estando um corpo animado, simultaneamente, de dois movimentos
perpendiculares entre si, o deslocamento na direção de um deles é
determinado apenas pela velocidade naquela direção.
Aplicações:
Problemas resolvidos:
1) O motor de um barco faz com que ele se desloque com velocidade de
4m/s. Um rio de 40m de largura flui com velocidade de 1m/s. Determine o
ponto em que o barco, partindo da posição mostrada, atinge a margem
oposta do rio.

R.: Podemos escrever a seguinte expressão para a velocidade resultante v R :
    
vR v rio vbarco 1,0.i 4,0. j

vR 17m / s
O tempo de travessia pode ser estimado por:
y 40
t 10 s
vy 4
x v x .t 10 .1 10 m
Portanto, o barco atinge a margem oposta do rio 10m abaixo do ponto de partida.
2) Uma partícula tem movimento definido pelas equações temporais
seguintes:
1 3 1 2
x .t 2.t 2 e y .t 2.t
3 2
49

50. sendo x e y expressos em metros e t em segundos. Determine a velocidade
e a aceleração no instante 3s.
R.: As componentes x e y da velocidade são expressas, em unidades SI, por:
dx
vx t 2 4.t
dt
dy
vy t 2
dt
Para o instante t=3s, temos:
vx 3m / s
vy 1m / s
Recompondo a velocidade:
2 2
v vx vy 10m / s
As componentes x e y da aceleração são expressas, em unidades SI, por:
dv x
ax 2.t 4
dt
dv y
ay 1
dt
Para o instante t=3s, temos:
ax 2m / s 2
ay 1m / s 2
Recompondo a aceleração:
2 2
a ax ay 5m / s 2
3) Uma partícula descreve uma hipérbole retangular dada pelas equações
seguintes:
x et / 2 e y e t / 2
50

51. sendo x e y expressos em metros e t em segundos. Determine a velocidade
e a aceleração no instante 1s.
R.: As componentes da velocidade nas direções x e y são obtidas de:
dx 1 t2 dy 1 t
2
vx .e vy .e
dt 2 dt 2
As componentes da aceleração, por sua vez, se expressam por:
dv x 1 t2 dv y 1 t
ax .e ay .e 2
dt 4 dt 4
No instante t=1s, temos:
vx 0,82 m / s ax 0,41m / s 2
vy 0,30 m / s ay 0,15m / s 2
Portanto:
2 2
v vx vy 0,82 2 ( 0,30) 2 0,87m / s
2 2
a ax ay 0,412 0,152 0,44m / s 2
O caso particular do movimento de um projétil
Uma vez que a aceleração da gravidade atua sempre na direção vertical, o
movimento de um projétil pode ser mais facilmente estudado a partir das
componentes retangulares das variáveis cinemáticas. Assim, são descritos
um movimento na direção horizontal e um movimento na direção vertical.
O projétil lançado se move sob ação de uma força constante, a da
gravidade, orientada para baixo. O movimento realizado é bidimensional.
51

52.   
vo (vx )o .i (vy )o . j
(v x ) o vo . cos o
(v y ) o vo .sen o
Na análise do lançamento de projéteis podemos, muitas vezes, desprezar
os efeitos da resistência do ar. Desse modo, desenvolvem-se um
movimento uniforme (velocidade constante) na direção horizontal e um
movimento uniformemente variado (aceleração constante, correspondente à
aceleração da gravidade g) na direção vertical.
dv x
ax 0
dt
dv y
ay g
dt

Admitamos que uma partícula seja lançada com velocidade inicial v o ,
segundo uma direção inclinada o com a horizontal. A figura seguinte
apresenta a trajetória de um projétil em condições ideais.
52

53. Conhecidos os valores de o e v o , podemos, a cada instante t, determinar
as componentes v x e v y . Assim:
vx (v x ) o
vy (v y ) o g.t
Durante o movimento bidimensional, a partícula acelera para baixo. Os
 
vetores posição r e velocidade v variam continuamente.
O movimento horizontal e o movimento vertical podem ser tratados de
forma independente. Isso facilita sobremaneira o procedimento analítico do
lançamento oblíquo.
Movimento horizontal:
x vx . t
x xo (vo . cos o ).t
Movimento vertical:
g .t 2
y (v y ) o .t
2
53

54. g.t 2
y yo (vo .sen o ).t
2
vy (v y ) o g.t
vy vo. sen o g .t
2 2
vy (vy )o 2.g. y
2
vy (vo .sen o )2 2.g.( y yo )
Trajetória:
Para caracterizar a trajetória, isto é, obter a função y=f(x), devemos
simplesmente eliminar a variável independente t nas equações
precedentes. Assim:
x xo (vo . cos o ).t
g.t 2
y yo (vo .sen o ).t
2
2
( x xo ) g x xo
y yo vo .sen o . .
vo . cos o 2 vo . cos o
g
y yo tg o .(x xo ) 2
.(x xo ) 2
2.(vo . cos o )
Assumindo xo 0 e yo 0 , encontramos:
54

55. g
y (tg o ).x 2
.x 2
2.(vo . cos o )
Note-se que g, o e vo são valores constantes. A equação obtida apresenta,
assim, a forma y a.x 2 b.x c , que retrata uma parábola em gráfico
cartesiano.
Alcance horizontal (R):
x xo R
y yo 0
x xo (vo . cos o ).t R
g.t 2
y yo (vo . sen o ).t 0
2
Eliminando a variável t nas duas equações anteriores, temos:
R g.R 2
vo .sen o . 0
vo . cos o 2.(vo . cos o ) 2
g.R
tg o
2.v . cos 2
2
o o
2.vo .tg o . cos 2
2
o
2
2.vo .sen o . cos o
2
vo .sen (2 o )
R
g g g
55

56. dR
Fazendo 0 , podemos deduzir que o máximo alcance ocorre
d o
quando o=45
o. Nesse caso:
2
vo
R máx
g
Altura máxima (h):
Determinamos a altura máxima (h) alcançada pelo projétil atribuindo valor
nulo à componente vertical da velocidade (vy). Assim:
v o . sen 2
2
o
h
2. g
Aplicações:
Problemas resolvidos:
1) Uma bolinha de aço desliza sobre a superfície plana de uma mesa com
velocidade de 1,0m/s. Sabendo-se que a mesa está a 2,0m do solo,
determine a que distância d essa bolinha tocará o solo.
R.: A bolinha, a partir do instante em que abandona a mesa de altura h, realiza,
simultaneamente, um movimento uniforme (com velocidade vx=1m/s) na horizontal

e um movimento uniformemente variado (com aceleração da gravidade g ) na
vertical. Desconsiderando o efeito da resistência do ar, o tempo de queda pode ser
determinado por:
1 2.h
h .g .t 2 t 0,63s
2 g
56

57. Então, a distância d percorrida na horizontal é: d v x .t
d 1.0,63 0,63m
2) Um avião voa horizontalmente a uma
altura de 180m com velocidade de
240km/h, devendo lançar pacotes de
mantimentos de região de selva, onde não
há condições de pouso. Estime a que
distância do ponto de recepção devem ser
abandonados os pacotes.
R.: A exemplo do problema anterior, há dois movimentos simultâneos cumpridos
pelos pacotes a partir de seu lançamento da aeronave.
Os pacotes saem da aeronave com a mesma velocidade desta. Desprezando,
novamente, a resistência do ar, temos o seguinte tempo de queda:
2.h
t 6s
g
Durante esse tempo, cada pacote percorre horizontalmente com velocidade
constante ( v x 240 km / h 66 ,7m / s ) a distância d calculada por:
d v x .t 66 ,7.6 400 m
3) Um projétil é disparado de uma altura de 60m, com velocidade inicial de
120m/s, num ângulo de 30º com a horizontal. Determine: a) a distância
horizontal do ponto de lançamento àquele onde o projétil atinge o solo; ii) a
altura máxima, em relação ao solo, alcançada pelo projétil.
57

58. R.: Também nesta solução, estaremos desprezando a resistência do ar. Então, a
trajetória é descrita pela seguinte relação (situando a origem do sistema de
referência cartesiana no ponto de lançamento):
g
y (tg o ).x 2
.x 2
2.(vo . cos o )
10
y (tg 30).x 2
.x 2
2.(120. cos30)
A distância horizontal x corresponde à abscissa no ponto, pertencente à curva de
trajetória, cuja ordenada é -60m. Assim, resolvendo a equação do segundo grau,
obtemos: (a outra solução é imprópria, pois, pela configuração específica do problema,
inexiste abscissa negativa)
x 1343,4m
Para a determinação do ponto de altura máxima, podemos igualar a zero a derivada
da função da trajetória. Por outro lado, é fácil perceber que a máxima altura y
(medida a partir do nível de lançamento) corresponde ao ponto em que a
componente vertical da velocidade é nula. Assim:
2 2
vy (vo ) y 2.g. y
2 2
0 (120 .sen30 ) 2.10 . y
y 180m
Tomando por referência o nível do solo, temos altura máxima igual a 240m.
4) Um homem dispara uma arma diretamente contra um objeto. Por mera
coincidência, no exato momento do disparo, o objeto começa a cair
verticalmente. Analise se o projétil atingirá o alvo.
R.: Sim. A aceleração da gravidade entre o ponto de disparo e a linha vertical
age igualmente sobre a bala (projétil) de queda do objeto.
e o objeto, durante o movimento de
queda. A bala sofre, então, um
desvio vertical equivalente ao do
objeto, em relação à linha de queda.
A bala somente não atingirá o alvo
(objeto) se o seu alcance for inferior
à distância (medida na horizontal)
58

59. 5) Uma pedra é lançada obliquamente do ponto O e deve vencer um
obstáculo de altura h que se encontra a uma distância x à sua frente, como
mostra a figura seguinte. Indique como deverá ser feito esse lançamento.
Determine a menor distância horizontal entre os pontos O e P (abaixo d do
ponto de lançamento, como mostra a figura seguinte).
R.: Devemos impor a condição de o ponto C pertencer à região côncava delimitada
pela curva da trajetória (parábola com concavidade voltada para baixo).
g
h x.tg 2
.x 2
2.(vo . cos )
Na situação limite, o ponto C (de coordenadas (x,h)) corresponde ao ápice da
trajetória. Então, a distância horizontal entre os pontos O e P será dada por
d
x. 1 1
h
Movimento curvilíneo: componentes tangencial e normal
A velocidade de uma partícula é representada por um vetor sempre
tangente à sua trajetória. Porém, em geral, o vetor aceleração não é
tangente à trajetória.
Em algumas situações de movimento curvilíneo, é conveniente decompor a
aceleração numa componente segundo a tangente à trajetória e noutra
segundo a direção normal dessa trajetória.
59

60.  
v v.it

 dv
a
dt 
 dv  dit
a .it v.
dt dt
 
dit dit d ds
. .
dt d ds dt
60

61. 
dit  d 1 ds
Conhecidas as relações in , e v , podemos
d ds dt
escrever:
 dv  v2 
a .it .in
dt
  
a a t .it a n .in
O módulo da aceleração total é assim obtido:
a at2 2
an
A componente tangencial da aceleração ( at dv ) é responsável pela
dt
mudança da velocidade escalar da partícula.
A componente normal da aceleração ( a v2 ) é
n
responsável pela mudança na direção do movimento.
61

62. Seja, mais uma vez, o vetor-posição de um ponto material definido por:
   
r x.i y. j z.k
onde x, y e z são funções do tempo t. As componentes tangencial e normal
da aceleração podem ser expressas em termos dessas funções e de suas
derivadas de primeira e segunda ordem. Para isso, basta fazer:
 
v a
at 
v
    1
(v a ) (v a ) 2
an 
v
Assim:
dx d 2 x dy d 2 y dz d 2 z
. . .
at dt dt 2 dt dt 2 dt dt 2
1
2 2 2 2
dx dy dz
dt dt dt
1
2 2 2 2
dx d 2 y dy d 2 x dy d 2 z dz d 2 y dz d 2 x dx d 2 z
. . . . . .
dt dt 2 dt dt 2 dt dt 2 dt dt 2 dt dt 2 dt dt 2
an 2 2 2
dx dy dz
dt dt dt
Por sua vez, o raio de curvatura da trajetória descrita pelo mesmo ponto
material pode ser expresso por:
62

63. 3
2 2 2 2
dx dy dz
dt dt dt
1
2
2 2 2
dx d 2 y dy d 2 x dy d 2 z dz d 2 y dz d 2 x dx d 2 z
. . . . . .
dt dt 2 dt dt 2 dt dt 2 dt dt 2 dt dt 2 dt dt 2
As relações acima permitem a análise e descrição do caso mais geral de
movimento. No caso particular em que o movimento se desenvolve no plano
x-y, ou seja, em que a trajetória pode ser expressa por
y f (x) , temos:
3
2 2
dy
1
dx
d2y
dx 2
Observação: O movimento de um projétil lançado obliquamente bem poderia ser
analisado e descrito com base nas equações agora apresentadas. No entanto, seria
bem mais laborioso do que foi feito a partir da decomposição do movimento em dois
eixos perpendiculares, convenientemente escolhidos.
Aplicações:
Problemas resolvidos:
1) Considere um veículo que se desloca à velocidade de 40m/s, segundo
uma curva de raio 1000m. Num dado instante os freios são acionados,
imprimindo uma desaceleração constante e fazendo com que, 10s depois, o
veículo apresente velocidade de 30m/s. Determine a aceleração desse
veículo imediatamente após a aplicação dos freios.
R.: O módulo da aceleração normal (centrípeta) é determinado por:
v2 40 2
a cp 1,6m / s 2
1000
O módulo da aceleração tangencial é determinado por:
63

64. v 10
at 1,0m / s 2 (de orientação contrária à da velocidade)
t 10
Então, o módulo da aceleração total se obtém de:
a at2 2
acp
a 1,0 2 1,6 2 1,89m / s 2
2) Um projétil é lançado obliquamente num ângulo com a horizontal,
sendo a velocidade inicial vo. Determine o raio mínimo de curvatura da
trajetória descrita por esse projétil.
R.: O raio de curvatura diminui com a diminuição da velocidade v ou com o aumento
de a n .
A velocidade é mínima no ponto
mais alto da trajetória ( v y 0 e
v v x ).
Nesse ponto, a aceleração da gravidade tem caráter de aceleração centrípeta.
Assim:
an g
vx v o . cos
64

65. v2 v2
an
an
vo . cos 2
2
g
Movimento curvilíneo: componentes radial e transversal
Em alguns problemas relacionados a movimento no plano, convém
definirmos a posição da partícula por suas coordenadas polares r e
(distância e ângulo), como mostra a figura seguinte.

 dr
v
dt 
 dr  d ir
v .ir r.
dt dt

 dr  d d ir
v .ir r. .
dt dt d
65

66. 
d ir 
Sendo i , temos:
d
 dr  d 
v .ir r. .i
dt dt
  
v v r .ir v .i
dr d
vr v r.
dt dt
  
 dv d 2r  dr dir dr d  d2  d di
a .ir . . .i r. 2 .i r. .
dt dt 2 dt dt dt dt dt dt dt
 
dir d  di d 
.i e .ir
dt dt dt dt

di 
Reconhecendo que ir :
d
2
 d 2r d  d2 dr d 
a r. .ir r. 2. . .i
dt 2 dt dt 2 dt dt
  
a a r .ir a .i
66

67. O módulo da aceleração total é assim obtido:
a a r2 a2
Para o caso particular em que a partícula descreve uma circunferência de
centro em O (movimento circular), temos:
dr d 2r
0 e 0
dt dt 2
Portanto:
 d 
v r. .i
dt
2
 d  d2 
a r. .ir r. 2 .i
dt dt
Aplicações:
Problemas resolvidos:
1) 0 braço mostrado na figura seguinte tem comprimento 1m e gira em torno
de O, segundo a relação 0,1.t 2 , onde se expressa em radianos e
t em segundos. O colar B desliza, de modo que o seu deslocamento em
relação ao ponto de rotação O é dado por r 0,8 0,1.t 2 , com r em
67

68. metros e t em segundos. Determine a velocidade e a aceleração quando
45o .
R.: As componentes radial e transversal da velocidade são obtidas como segue:
dr
vr 0,2.t
dt
d
v r. (0,8 0,1.t 2 ).0,2.t 0,16.t 0,02.t 3
dt
Por sua vez, as componentes radial e transversal da aceleração se expressam por:
2
d 2r d
ar r. 0,2 (0,8 0,1.t 2 ).0,2 0,36 0,02.t 2
dt 2 dt
d2 dr d
a r. 2 2. .
dt dt dt
2
a (0,8 0,1.t ). 0,2 2.( 0,2.t ). 0,2.t 0,16 0,1.t 2
Determinemos, então, o instante em que é igual a 45º( /4 rad).
0,1.t 2 t 2,8s
4
Aplicando o valor de t nas expressões acima, encontramos:
vr 0,56 m / s
v 8,96 .10 3 m / s
Daí o módulo da velocidade: v 0,56m / s
2
ar 0,20 m / s
a 0,62 m / s 2
Daí o módulo da aceleração: a 0,65 m / s 2
68

69. 2) A figura seguinte ilustra o vôo de um foguete disparado verticalmente no
ponto B, o qual é rastreado por um radar situado no ponto A. Expresse a
velocidade e a aceleração desse foguete, em termos da distância b, do
ângulo e das derivadas deste em relação do tempo.
R.: Pela geometria do problema, reconhecemos as seguintes relações:
vr
v
sen
b
r
cos
b.sen d
vr .
cos2 dt
b.sen d 1
Daí, v 2
. .
cos dt sen
d
v b. sec2 .
dt
69

70. Movimento relativo de duas partículas
Há situações em que vários sistemas de referência são utilizados
simultaneamente, sendo um deles fixo (em geral, relativamente à Terra8) e
os demais móveis.
Consideremos um sistema de referência em translação (Ax’y’z’, na figura
seguinte), relativamente ao sistema fixo Oxyz. Se duas partículas A e B se
 
deslocam no espaço e rA e rB são, respectivamente, as suas posições em
relação ao sistema Oxyz, temos:
  
Posição rB rA rB / A

 drB
Velocidade vB
dt
  
vB vA vB / A
8 Na cinemática, a eleição de um sistema de referência fixo é bastante flexível, ou seja,
puramente arbitrária. O mesmo não se pode afirmar na abordagem da dinâmica, em que se
estudam as causas (forças) e os efeitos (movimentos). Conforme será visto adiante, a
definição de sistema referencial inercial é bem mais rigorosa.
70

71. 
 dv B
Aceleração aB
dt
  
aB aA aB / A
O movimento de B, considerado o referencial fixo Oxyz, é dito movimento
absoluto e pode ser obtido, então, combinando-se o movimento de A com o
movimento relativo de B, tomado o referencial móvel em A.
Aplicações:
Problemas resolvidos:
1) Dois veículos se aproximam do cruzamento de ruas mostrado na figura
seguinte. Num dado instante, o veículo A, distante 20m do cruzamento,
apresenta velocidade de 15m/s e o seu motorista o freia a 2m/s², enquanto
o veículo B, distante 15m do cruzamento, tem velocidade de 20m/s e o seu
motorista o acelera a 2m/s². Determine: i) a velocidade de B em relação a
A; ii) a aceleração de B em relação a A.
R.: Vamos estabelecer um sistema de eixos cartesianos orientado como na figura
seguinte. Podemos escrever:
  
y vB v A vB / A
  
20 . j 15 .i v B / A
  
x vB / A 15 .i 20 . j

vB / A ( 15) 2 ( 20) 2 25m / s
71

72. 20
direção: arctg
15
  
aB a A aB / A
  
2. j 2.i a B / A
  
a B / A 2.i 2. j

aB / A 22 ( 2) 2 2 2m / s 2
2
direção: arctg
2
2) Durante uma chuva em que as gotas de água caem verticalmente com
velocidade vc, um veículo encontra-se em movimento horizontal com
velocidade vv. Como um passageiro, no interior do veículo e olhando
lateralmente, vê as gotas descerem?

R.: Devemos determinar a velocidade da chuva em relação ao veículo ( vV / C ).
  
vV / C vchuva vveículo
A figura seguinte esclarece.
3) Considere duas pequenas aeronaves, A e B, voando à mesma altitude,
como mostrado na figura seguinte. A velocidade da aeronave da esquerda
 
(A) v A ; a da aeronave da direita (B), v B . O ângulo é medido entre seus
cursos em linha reta. Determine a velocidade de B em relação a A.
72

73. R.: Aplicando a expressão da velocidade relativa:
  
vB v A vB / A
  
vB / A vB v A
Movimentos dependentes
Há situações em que partículas encontram-se interligadas, normalmente por
cordas ou cabos em associação a polias, de forma que o movimento de uma
delas depende do movimento da outra. Consideremos o exemplo da figura
seguinte, em que o bloco B desce um plano inclinado obrigando o bloco A a
deslocar-se para cima num outro plano.
73

74. Podemos escrever, sendo inextensível o comprimento l da corda que
interliga os blocos A e B:
SA l CD SB l
onde lCD é o comprimento (constante) da corda entre os pontos C e D. As
expressões seguintes são válidas:
dS A dlCD dSB dl
dt dt dt dt
dS A dSB
0
dt dt
vB vA
Analogamente, chegamos a:
aB aA
As relações encontradas são úteis no equacionamento de problemas que
envolvam corpos interligados e que apresentem, portanto, movimentos
dependentes.
À guisa de ilustração, para que o leitor se familiarize com a forma de
estabelecimento das relações entre velocidades e acelerações, que são
específicas a cada situação, apresentamos, a seguir, dois exemplos
aplicativos envolvendo polias (fixas e / ou móveis) e cordas.
74

75. SA 2.S C l1
S B ( S B S C ) l2
(l1 e l2 são os comprimentos de cabo
remanescentes)
Daí: S A 4.S B 2.l2 l1
Derivando em relação ao tempo:
vA 4.vB 0
SC SB l1
( S A S C ) ( S B S C ) S B l2
(l1 e l2 são os comprimentos de cabo
remanescentes)
Daí: S A 4.S B 2.l1 l2
Derivando em relação ao tempo:
vA 4.vB 0
75

76. Aplicações:
Problemas resolvidos:
1) Na situação mostrada na figura ao
lado, o bloco A desce com velocidade de
4,5m/s. Determine a velocidade do bloco
B.
R.: Neste caso, temos a seguinte relação: (os segmentos negritados do cabo,
por serem de extensão inalterável, estão descontados; ou seja, l se refere apenas
aos segmentos do cabo que mudam de extensão durante o movimento)
S A 3.S B l
Aplicando a derivada temporal:
vA 3.vB 0
Portanto, a velocidade de A é o triplo da velocidade de B, porém orientada
contrariamente, ou seja, a velocidade de B (que sobe) vale 1,5m/s.
2) Uma corda inextensível é
puxada para a esquerda, à
velocidade constante de módulo v,
com o objetivo de erguer um bloco
a partir do chão. Expresse a
velocidade e a aceleração do bloco
em função do tempo.
76

77. R.: Seja l o comprimento total do cabo que está sendo puxado para a
esquerda. Podemos expressá-lo por:
l h2 x2 (h y)
2 2
y h x (l h)
dy 1 2.x dx
vC . .
dt 2 h 2
x 2 dt
Então, a velocidade de ascensão do bloco assim se relaciona com a velocidade da
outra extremidade da corda:
x
vC .v
h x2
2
Apesar de ser constante a velocidade v, a velocidade do bloco é variável, pois
quando a extremidade da corda se movimenta para a esquerda não apenas ocorre
mudança na direção do primeiro segmento da corda, mas também no seu
comprimento.
Podemos obter a aceleração do bloco derivando mais uma vez a variável (altura) y
em relação ao tempo. Assim:
dx
x.
d2y dt .x. dx 1 dx dx 1 d 2x
aC 2 3
. . .x. 2
dt h2 x 2 2 dt h2 x 2 dt dt h2 x 2 dt
h 2 .v 2
aC 3
h2 x2 2
77

78. As leis de Newton da dinâmica
A s leis gerais do movimento de um corpo submetido a forças foram
apresentadas por Isaac Newton em 1687, em seu livro Philosophiae
naturalis principia mathematica.
Na sua forma original, as leis de Newton assim se expressam:
LEX I Corpus omne persevere in statu suo
quiescendi vel movendi uniformiter in directum,
nisi quatenus a viribus impressis cogitur statum
illum mutare.
LEX II Mutationem motus proportionalem esse vi
motrice impressae et fieri secundum lineam
rectam qua vis illa imprimitur.
LEX III Actioni contrariam semper et aequalem
esse reactione: sive corporum duorum actiones in se
mutuo semper esse aequales et in partes contrarias
dirigi.
Num primeiro momento, essas leis podem ser enunciadas assim:
Primeira lei:
Todas as coisas permanecem em repouso ou se movem em linha reta na
mesma velocidade, a não ser que uma força aja sobre elas.
Todo corpo em repouso tende a permanecer em repouso.
Todo corpo em movimento tende a continuar em movimento.
Segunda lei:
Se a força resultante atuante sobre um ponto material é diferente de zero,
esse ponto adquire aceleração proporcional ao módulo da resultante e na
direção e sentido dessa resultante.
78

79. Terceira lei:
A cada ação está sempre oposta uma reação.
As ações mútuas de dois corpos um sobre o outro são sempre iguais
e dirigidas para as partes contrárias.
Ao estudarmos a estática, com os corpos em equilíbrio, extensivamente
empregamos a primeira e a terceira leis de movimento de Newton. Pela
primeira lei, temos que a resultante das forças que agem sobre um corpo
em equilíbrio é nula; ou ainda, sempre a força resultante for nula, o corpo
estará em equilíbrio, seja em repouso, seja em movimento com velocidade
(vetorial) constante. Assim, um corpo tende a permanecer como está, a
menos que forças atuem sobre ele. De acordo com a terceira lei, quando
um corpo exerce uma força sobre outro, este reage e exerce sobre o
primeiro uma força diretamente oposta; isso significa que as forças sempre
aparecem aos pares. Para a abordagem da dinâmica das partículas, essas
duas leis também são úteis e seriam suficientes para o estudo do
movimento de corpos que não apresentam aceleração. Quando há
aceleração, ou seja, quando a velocidade varia, seja em módulo, seja em
direção, a segunda lei de Newton passa a ser fundamental para relacionar o
movimento com as forças atuantes sobre o corpo.
Consideremos, inicialmente, um mesmo ponto material submetido, em
  
momentos distintos, às forças F1 , F2 e F3 , como mostrado na figura
seguinte. A aceleração, que é uma grandeza vetorial, terá, em cada caso, a
direção e sentido indicados – sempre a mesma direção e sentido da força.
79

80.  
Ao determinarmos a razão entre os módulos de F e a , observamos que a
relação entre F1 e a1 é igual à relação entre F2 e a2, que por sua vez é igual
à relação entre F3 e a3.
Assim:
F1 F2 F3
... cons tan te
a1 a2 a3
A relação constante obtida entre o módulo da força e o valor da aceleração
corresponde a uma característica do ponto material considerado, que
denominamos massa do ponto material.
Podemos, então, apresentar a formulação da segunda lei de Newton:
 
F m.a
onde m é a massa (grandeza escalar) que multiplica uma grandeza vetorial,
 
a aceleração a . E assim se obtém uma grandeza vetorial: a força F .

No caso mais geral, em que a força F não é constante, porém variável

com o tempo, também a aceleração a será variável com o tempo. A
expressão acima, no entanto, continua válida para qualquer dado instante.
 
F (t ) m.a (t )
A primeira lei de Newton pode ser considerada um caso particular da

segunda lei: se a força resultante F sobre uma partícula é nula,
também nula será a aceleração, o que implica, para a partícula, manter
o seu estado de repouso ou de movimento retilíneo uniforme.
O enunciado da terceira lei de Newton (“A toda ação corresponde uma
reação igual e contrária, ou seja, as ações mútuas de dois corpos um sobre
80

81. o outro são sempre iguais e dirigidas em sentidos contrários”) sugere que
as forças, na natureza, sempre se manifestam aos pares. No entanto, não
se anulam mutuamente, pois estão sempre aplicadas a corpos distintos.
Na verdade, também a terceira lei de Newton é mais bem apresentada a
partir do princípio da conservação do momento linear (quantidade de
movimento), segundo o qual o momento total de um sistema isolado se
conserva.
Sobre o princípio da ação e reação, e para uma melhor discussão da
terceira lei de Newton, reproduzimos, a seguir, texto de Y. Perelman,
extraído de seu livro Física Recreativa.
81

82. UMA LEI DE DIFÍCIL COMPREENSÃO, Y. Perelman (Física Recreativa, vol. II)
Nenhuma das três leis fundamentais da mecânica enseja tantas
incompreensões como a "terceira lei de Newton", ou seja, a lei de ação e reação.
Todo mundo conhece essa lei e sabe aplicá-la em alguns casos, mas são raros
os que podem considerar isentos de certas dúvidas. Eu tenho de reconhecer que
só cheguei a compreender dez anos depois de tê-la estudado pela primeira vez.
Conversando com diversas pessoas, tenho que me convencer de que a
maioria delas estava disposta a reconhecer essa lei como certa, mas fazendo
algumas objeções substanciais. Muitos admitem que essa lei é justa quando se
trata de corpos em repouso, mas, em geral, não compreendem como é possível
aplicá-la às relações entre corpos em movimento. A ação, diz a lei, é sempre
igual e contrária à reação. Isso quer dizer que, se um cavalo empurra um carro
para frente, o carro empurra o cavalo para trás com a mesma força. Mas, por que
razão, nesse caso, o carro se move, se a as forças são iguais? Por que é que as
forças não se equilibram entre si?
Essas são dúvidas que surgem com a terceira lei de Newton. Isso
significa que a lei não é correta? Não, a lei é indiscutivelmente correta. Somos
nós que a compreendemos mal. As forças simplesmente não se equilibram entre
si porque estão aplicadas a corpos diferentes: uma delas no cavalo e a outra, no
carro. As forças são efetivamente iguais, mas, por acaso, forças iguais produzem
sempre os mesmos efeitos? Forças iguais comunicam a mesma aceleração a
todos os corpos? A ação de uma força sobre um corpo não depende, afinal, do
próprio corpo e da "resistência" que se opõe à força?
Se recorrer à memória sobre tudo isso, estará claro por que o cavalo
empurra o carro, apesar deste puxá-lo, em sentido oposto, e com a mesma força.
As forças que atuam sobre o carro e o cavalo são iguais entre si em cada
momento, mas como o carro se move livremente sobre as rodas, enquanto o
cavalo se apóia no solo, está claro por que ele avança com o carro. Se o carro
não se opuser à reação da ação à força motriz do cavalo, poderíamos dispensar
o cavalo e bastaria fazer qualquer força, por menor que fosse, para que o carro
se movesse. O cavalo se apóia no solo e, justamente por isso, vence a reação do
carro.
Isso tudo seria mais bem compreendido e com menos margem a
dúvidas se a lei não fosse abreviada como de costume: "a ação é igual à reação".
Sendo assim, por exemplo: "sempre que um corpo exerce sobre um outro uma
força (ação), este exerce sobre aquele outra força igual e diretamente oposta à
primeira (reação)". Dessa maneira, são as forças que são iguais, já que os efeitos
que produzem (essas medidas são feitas, comumente, pela translação de um
corpo) são, via de regra, diferentes, devido cada uma das forças estarem
aplicadas em corpos distintos.
A queda dos corpos também obedece à lei de ação e reação, embora
não seja fácil distinguir as duas forças. Quando uma maçã cai em direção à terra
(ao solo) é porque ela atrai a terra e esta, por sua vez, é atraída com a mesma
força pela maçã. Precisamente falando, a maçã cai em direção a terra e a terra
cai em direção a maçã, mas as velocidades com que caem são distintas. As
forças de atração, sendo iguais, comunicam a maçã uma aceleração de 10 m/s 2,
enquanto a aceleração comunicada a terra é tantas vezes menor quanto a massa
da terra é maior que a da maçã, ou seja, como a massa da terra é enormemente
maior do que a da maçã, a aceleração que recebe é tão insignificante que se
pode considerar igual a zero. Por isso, dizemos que a maçã cai em direção a
terra em vez de dizer que ambas, maçã e a terra, caem mutuamente, uma em
direção a outra.
82

83. Considerações sobre a variabilidade das forças
Em algumas situações práticas, podemos considerar forças que são
aproximadamente constantes, tornando a abordagem mais simples. São
exemplo disso, a força da gravidade próximo à superfície da Terra, a força
de atrito, dentre outras. Entretanto, em muitos casos, as forças atuam sobre
a partícula não são constantes, requerendo a utilização de técnicas
analíticas e numéricas para a solução dos problemas. Podemos, então,
destacar:
i. forças que dependem do tempo – ex.: força de frenagem de
um veículo; força que atua sobre cada molécula de ar onde se
está propagando uma onda sonora
ii. forças que dependem da velocidade – ex.: força de arraste
atuante sobre um corpo que se move através de um fluido
iii. forças que dependem da posição – ex.: força restauradora
exercida por uma mola esticada com um corpo preso a ela.
No caso de forças que dependem da posição, a análise do movimento é
mais facilmente conduzida através do método trabalho e energia, discutido
adiante.
As forças da natureza
Diferentes forças atuam na natureza. Todas elas, porém, podem ser
estudadas e compreendidas em termos de apenas quatro interações
básicas das partículas elementares.
As forças entre os corpos macroscópicos são atribuídas ou à força
gravitacional ou à força eletromagnética. São essas as forças que
observamos cotidianamente. Ambas constituem ação à distância, ou seja,
atuam entre partículas que estão separadas no espaço.
A interação gravitacional é a mais fraca de todas, sendo comum a todas as
partículas. A mais citada é o peso de um corpo nas proximidades da
superfície da Terra e corresponde à força gravitacional entre a Terra e esse
corpo. Os planetas no Sistema Solar são mantidos em órbita pela força
gravitacional do Sol, assim como a Lua mantém sua órbita por conta da
força gravitacional da Terra. Os oceanos terrestres estão sujeitos às forças
gravitacionais do Sol e da Lua, e daí decorrem as marés.
83

84. As partículas com carga elétrica estão sujeitas, ainda, à interação
eletromagnética. São de natureza eletromagnética, fruto da interação das
moléculas, forças exercidas por corpos que estão em contato uns com os
outros, como, por exemplo, a força normal, a força de atrito, a força elástica.
Entre prótons e nêutrons (partículas elementares do tipo hádrons) atua a
força nuclear forte, responsável pela estabilidade dos núcleos atômicos, e
se caracteriza pela diminuição acentuada com a distância. Uma
manifestação dessa força nuclear forte ocorre na explosão da bomba de
hidrogênio.
A quarta interação básica se refere à força nuclear fraca. Essa força é de
curto alcance e se manifesta entre léptons, como os elétrons, e entre
hádrons, como os prótons e os nêutrons. Ela responde, por exemplo, por
alguns decaimentos radiativos.
As forças eletromagnéticas e a nuclear fraca se combinam na força elétrica
fraca. A Grande Teoria da Unificação propõe uma combinação da força
nuclear forte com a força elétrica fraca; também se vislumbra a combinação
dessas com a força gravitacional. Está aí um dos desafios da física
moderna.
Para uma análise comparativa, podemos compor o seguinte quadro:
Força nuclear forte É a mais intensa de todas as forças; opera em
pequenas distâncias, de 10-15m ou menos
Força nuclear fraca Sua intensidade é de cerca de 10-8 da força nuclear
forte; opera em distâncias de 10-17m ou menos
Força eletromagnética Sua intensidade é de cerca de 10-3 da força nuclear
forte; opera em todas as distâncias
Força gravitacional É a mais fraca de todas as forças; sua intensidade é
estimada em 10-45 da força nuclear forte; opera em
todas as distâncias
Algumas forças particulares
- A força peso:
Também dita força gravitacional, o peso é a força com a Terra (corpo com
grande massa) atrai qualquer outro corpo próximo a ela. À força peso, está
associada à aceleração da gravidade.
 
P m.g
84

85. - A força de atrito:
O atrito decorre de irregularidades nas superfícies posta em contato.
Portanto, não se manifesta à distância. Uma característica dessa força é
que ela sempre se opõe à tendência do movimento, embora possa favorecer
diversos deslocamentos (como o de uma pessoa ao caminhar e o de um
veículo numa pista de rolamento).
Experimentalmente, observa-se que o módulo da força de atrito é
diretamente proporcional à força normal (exercida perpendicularmente ao
plano de contato).
Podem ser identificados dois tipos de força de atrito: estático ou cinético. O
primeiro, quando ainda não há movimento relativo entre as superfícies em
contato, embora já exista algum esforço tendente a isso. O atrito cinético se
apresenta em associação ao movimento. Verifica-se que a força de atrito
estático é, quase sempre, maior à força de atrito cinético (em geral, é mais
difícil pôr um corpo em movimento do que mantê-lo em movimento).
Fat e e .FN
Fat c c .FN
onde e e c são grandezas adimensionais denominadas,
respectivamente, os coeficientes de atrito estático e cinético.
Também se constata experimentalmente que a força de atrito não depende
da área das superfícies em contato.
Através de um experimento simples, pode ser estimado o valor do coeficiente de
atrito estático. Inicialmente, colocamos o corpo em repouso sobre a superfície
horizontal; sem tocar o corpo, inclinamos lentamente a superfície de apoio até que o
corpo atinja a iminência de movimento; nessa posição, medimos o ângulo
(declividade) entre a superfície e o plano horizontal; a tangente desse ângulo
corresponderá ao valor do coeficiente de atrito (para melhor inferência, o
experimento deve ser repetido algumas vezes).
Note-se que o coeficiente de atrito estático se refere ao valor máximo da força de
atrito antes que o movimento seja iniciado, ou seja, a força de atrito estático evolui
de zero (quando nenhuma força é aplicada tendente a movimentar o corpo) até um
valor máximo e .FN (em via de efetivação imediata do movimento).
85

86. - A força elástica:
A força elástica decorre de uma deformação sobre um corpo com
capacidade de se recompor. Essa força tem sempre caráter restaurador,
estando, por isso, sempre orientada para a sua posição indeformada. Ou
seja, a força elástica tem sentido contrário ao da força externa aplicada para
promover a deformação da mola.
O módulo da força exercida sobre uma mola elástica linear deformada de x
é
Fel k .x
onde x pode corresponder a um alongamento (no caso de tração) ou a uma
contração (no caso de compressão da mola). A relação acima expressa a lei
de Hooke e tem sua validade restrita à faixa de comportamento elástico da
peça ou material; havendo deformação plástica, a mola não recupera
completamente a sua configuração inicial.
- A força de arraste:
Essa força se manifesta, por exemplo, sobre um corpo que se desloca num
fluido (ar, água etc), tendente a reduzir a sua velocidade. Basicamente, a
força de arraste depende da forma do corpo, da natureza do fluido e da
velocidade do corpo relativamente ao fluido – a força de arraste aumenta
com o aumento da velocidade.
Experimentalmente, verifica-se que para velocidades elevadas, a força de
arraste é aproximadamente proporcional ao quadrado da velocidade,
enquanto, para velocidades baixas, a força de arraste é aproximadamente
proporcional à velocidade do corpo.
Se considerarmos um corpo de massa m caindo verticalmente no ar, sob força
constante da gravidade, podemos expressar a resultante das forças verticais
(direção y):
F m.g b.v n m.a y
onde b é uma constante dependente da forma do corpo e das características do ar;
n assume valores próximos a 1 ou a 2, em função da velocidade.
Durante a queda desse corpo, à medida que a velocidade aumenta, também
aumenta a força de arraste. Após algum tempo de queda, a força de arraste tende a
equilibrar a força da gravidade; quando isso ocorre, o corpo passa a descer em
velocidade constante, comumente denominada velocidade terminal (ou final).
86

87. Aplicações:
Problemas resolvidos:
1) Os blocos A e B da figura seguinte, de massas 4kg e 2kg,
respectivamente, estão apoiados num plano horizontal perfeitamente liso.

Ao bloco A, aplica-se a força F de intensidade 18N. Determine a força de
contato entre os dois blocos.

R.: Os blocos A e B adquirem igual aceleração. Portanto, a intensidade da força F
aplicada se distribui proporcionalmente às massas. Podemos escrever:
 
F (m A m B ).a
O módulo da aceleração vale:
F 18
a 3m / s 2
mA mB 6
A força de contato entre os dois blocos é a que confere a B a aceleração obtida de
3m/s2. Ou seja, 6N.
2) No sistema mostrado na figura seguinte, o corpo A, de 3kg, apresenta
movimento uniforme. O bloco B, de massa 10kg, está ligado ao bloco A por
um fio inextensível, de massa desprezível. Determine o coeficiente de atrito
dinâmico entre o corpo B e o seu plano de apoio.
R.: Os blocos A e B apresentam aceleração de mesmo módulo. Sobre o bloco A
atuam a força peso (de A) e a força de tração transmitida pelo fio. Sendo nula
aceleração de A (movimento uniforme), também nula será a aceleração de B. Para
87

88. isso, o peso de A deve ser equivalente à força de tração que puxa B para a direita.
Assim:
m A .g T m A .a 0
T Fat B m B .a 0
Portanto, o peso de A tem o mesmo valor (intensidade) que a força de atrito que
atua sobre B.
m A .g m B .g . c
mA
Daí:
mB
3) No sistema mostrado na figura seguinte, inexiste atrito entre o bloco A e
o plano inclinado. Os blocos A e B têm, cada um, massa de 4kg. O fio que
interliga os dois blocos é inextensível e de massa desprezível. Determine: i)
a aceleração dos blocos; ii) a tração no fio.
R.: Sobre o bloco B, atuam a força peso (de B) e a força de tração (pelo fio). Sobre
o bloco A, atuam o seu peso a força normal (aplicada pelo plano inclinado) e a força
de tração transmitida pelo fio. Ambos os blocos apresentam aceleração de mesmo
módulo. Assim, podemos escrever:
mB .g T mB .a
T m A .g.sen30 o m A .a
Substituindo os valores e resolvendo o sistema, encontramos:
aA aB a 2,5m / s 2 e T 30N
4) Um corpo de massa 3kg, inicialmente em repouso, passa a estar
  
submetido a uma força F 3.i 2. j . Determine a velocidade desse
corpo após 3s.
R.: Aplicando a segunda lei de Newton, determinamos a aceleração do corpo:
88

89.  
F m.a
  2 
a 1.i .j
3
vx vox a x .t e v y voy a y .t
vx 0 1.t para t 3s : v x 3m / s
2
vy 0 .t para t 3s : v y 2m / s
3  

Portanto, em t 3s , a velocidade se expressa por v 3.i 2. j , cujo
módulo é 13 m / s .
5) Um bloco de massa m1 escorrega sobre outro de massa m2. As
superfícies em contato não apresentam atrito. Determine: i) a aceleração de
cada bloco; ii) a tensão no fio que passa pela polia.
R.: Temos os seguintes diagramas de corpo livre para os blocos 1 e 2:
Os dois blocos adquirem aceleração de mesmo módulo.
Podemos estabelecer as relações:
P1 .sen T m1 .a
89

90. T P2 .sen T m2 .a
Daí: ( P2 P1 ).sen (m1 m2 ).a
g .( m1 m 2 ).sen
a
m1 m 2
g .( m1 m2 ).sen
T m2 .g .sen m2 .
m1 m2
m1 m2
T m2 .g.sen . 1
m1 m2
m1 m2
ou T m1 .g.sen . 1
m1 m2
6) No sistema mostrado na figura seguinte, um bloco de massa 2kg é
lançado para baixo, a partir do ponto A, com velocidade de 4m/s. O
coeficiente de atrito entre o bloco e o plano inclinado é 0,30. Determine a
distância percorrida pelo bloco até parar.
R.: O bloco sobre o plano inclinado está sujeito às forças peso, normal e de atrito.
Assim, na direção do deslocamento:
m.g.sen15 m.g. cos15.0,30 m.a
2
a 0,31m / s
O sinal negativo indica que a aceleração tem sentido contrário ao da velocidade.
Aplicando a expressão da cinemática para o movimento uniformemente variado:
v2 2
vo 2.a. s
2 2
0 4 2.( 0,31). s s 25,8m
Portanto, o corpo pára após percorrer 25,8m ao longo do plano inclinado.
90

91. 7) Considere o sistema mostrado na figura seguinte. Os blocos A e B têm
massas 10kg e 5kg, respectivamente. Entre os blocos A e B, bem como
entre o bloco A e a superfície sobre a qual se encontra, o coeficiente de
atrito vale 0,25. Inexiste atrito entre o cabo e a roldana. Determine: i) a
aceleração do bloco A; ii) a tensão no cabo.
R.: Temos os seguintes diagramas de corpo livre para os blocos A e B:
Podemos, então, estabelecer as seguintes relações algébricas:
150 T Fat A Fat B m A .a A
Fat A c .FNA c .( FNBA PA ) c .( FNBA m A .g )
FNAB FNBA PB m B .g
Fat B c .FNAB
T Fat B m B .a B
aA aB a
Substituindo os valores e resolvendo o sistema de equações, encontramos:
a 5,83 m / s 2 e T 41,70 N
8) Os dois blocos A e B, mostrados na figura seguinte, têm massas,
respectivamente, 100kg e 200kg. O sistema parte do repouso.
Considerando que o plano horizontal e a roldana sejam perfeitamente
91

92. polidos e que a massa da roldana seja desprezível, determine: i) a
aceleração de cada bloco; ii) a tensão em cada corda.
R.: Temos as seguintes relações cinemáticas:
v A 2.v B e aA
2.a B

A corda presa em B suporta uma tração ( T1 ) com o dobro da intensidade

da tração ( T 2 ) da corda presa em A.
Aplicando a segunda lei de Newton:
mB .g T1 mB .a B
T2 m A .a A
Então: m B .g 2.T2 mB .a B
mB .g 2.m A .a A mB .a B
mB .g 4.m A .a B mB .a B
Substituindo os valores e resolvendo o sistema, encontramos:
aA 6,67 m / s 2 ; a B 3,33 m / s 2 ; T1 1334 ,0 N e T2 667 ,0 N
9) Para o sistema mostrado na figura
seguinte (máquina de Atwood), determine:
i) a expressão para a aceleração da massa
M; ii) a expressão para a tensão da corda.
92

93. R.: Considerando que o fio seja inextensível e que tenha massa desprezível,
podemos assumir que a tensão é a mesma em todos os pontos desse fio. Então,
aplicando a segunda lei de Newton a cada uma das massas (m e M),
separadamente, temos:
m.g T m.a m
M .g T M .a M
É fácil perceber que a M a m a , isto é, a aceleração com que um dos
corpos desce tem o mesmo módulo da aceleração com que o outro corpo sobre, já
que o fio é inextensível. Assim:
M .g m.g M .a m.a
E daí:
M m
a .g
M m
2.m.M
T .g
M m
10) No sistema mostrado na figura seguinte, uma mola de comprimento
normal l e constante elástica k tem uma extremidade presa ao suporte A e a
outra no colar de massa m. Não há atrito entre o colar e a barra horizontal.
Encontre a expressão da aceleração do colar em termos da distância x.
R.: Sobre o colar, na direção da mola, atua a força elástica (restauradora, orientada
de B para C):
Fel k. l 2 x2 l
Aplicando a segunda lei de Newton:
k. l l2 x 2 . cos m.a x
onde é o ângulo a direção da mola e eixo da barra horizontal.
93

94. x
k. l l2 x2 . m.a x
2
l x2
k .x l
ax .1
m x2 l2
11) Considere um corpo de massa m abandonado de uma certa altura no ar.
Encontre a expressão da velocidade terminal.
R.: A velocidade terminal é alcançada quando a força gravitacional é igual à força
de arraste (devido ao deslocamento do corpo num meio fluido). Assim, aplicando a
segunda lei de Newton, para a direção vertical (de queda):
m.g b.v n m.a y 0
n
m.g b.v
Daí:
1/ n
m.g
vt
b
12) Analisando a resposta à questão anterior, comente o projeto de um
veículo de Fórmula 1 e o de um pára-quedas.
R.: O projetista deve levar em conta que a velocidade terminal é função, sobretudo,
do parâmetro b, o qual depende do formato (da aerodinâmica) do equipamento que
estará se deslocamento no ar. Assim, quanto menor o valor de b, maior o valor da
velocidade terminal. Na concepção de um pára-quedas, interessa que ele opere
com uma velocidade terminal pequena, para atenuar o risco durante a descida e
aliviar o choque com a superfície do solo. Por outro lado, no caso do carro de
corrida, como a resistência do ar tende a atrapalhar o seu desempenho e aumentar
o consumo de combustível, quanto menor essa resistência, melhor, ou seja, o
projetista deverá modelar o veículo com o menor b possível.
13) Seja um corpo de massa m que cai sob ação da gravidade e de uma
força de arraste expressa por FD b.v , onde v é a velocidade e b uma
constante que depende da forma do corpo e das propriedades do ar.
Encontre as expressões horárias da aceleração e da velocidade.
R.: Orientando o sistema de referência verticalmente para baixo e aplicando a
segunda lei de Newton ao movimento, temos:
94

95. dv b
a g .v
dt m
dv g
.dt
v vf vf
m.g
Sendo a velocidade terminal expressa por vf
b
b.t g .t
m.g m vf
v .1 e vf . 1 e
b
14) Considere um objeto caindo de uma grande altura. Encontre a
expressão da distância percorrida até que esse objeto alcance a metade de
sua velocidade terminal, assumindo que a força de arraste (resistência do
ar) seja proporcional ao quadrado da velocidade.
R.: Sobre o objeto atuam, basicamente, duas forças: a da gravidade (peso) e a de
arraste. Aplicando a segunda lei de Newton, temos:
m.g b.v 2 m.a
b.v 2
a g
m
dv dv ds dv
m. m. . m.v.
dt ds dt ds
dv b 2
v. g .v
ds m
b 2
v.dv ( g .v ).ds
m
vf / 2
v
Temos, então, que calcular h .dv
b 2
0 g .v
m
95

96. vf / 2
1 g
h . ln v2
b b
2.
m m 0
b g
lembrando que (pois na velocidade terminal, a aceleração resultante é
m v2
f
nula )
v2
f 3
h . ln
2.g 4
v2
f
h 0,1438.
g
Partícula em equilíbrio
O equilíbrio de uma partícula pressupõe a ausência de aceleração. Sendo
esta nula, duas situações podem ocorrer: a partícula em trajetória retilínea
com velocidade constante ou a partícula se encontra em repouso. No
primeiro caso, dizemos que o equilíbrio é dinâmico; no outro, o equilíbrio é
estático.
Portanto, a condição a ser atendida para que o equilíbrio se verifique é a
seguinte:

F 0
Equivalentemente:
  
Fx .i Fy . j Fz .k 0
ou Fx Fy Fz 0
96

97. Aplicações:
Problemas resolvidos:
1) Considere uma partícula em
equilíbrio estando submetida às
  
forças F1 , F2 e F3 . Mostre que
  
F1 F2 F3
sen sen sen
   
onde: é o ângulo entre F2 e F3 ; , o ângulo entre F1 e F3 , e ,o
 
ângulo entre F1 e F2 .
R.: Uma maneira de se verificar o equilíbrio de forças é dispondo os vetores que as
representam de forma seqüenciada (justando a origem de um vetor com a
extremidade de outro vetor). Se a figura assim obtida for um polígono (linhas
poligonais fechadas), a soma vetorial dessas forças é igual a zero e, portanto, a
partícula a elas submetidas estará em equilíbrio (porém, não necessariamente em
repouso). A figura seguinte esclarece.
Aplicando a lei dos senos, chegamos à conclusão de que a relação proposta no
enunciado da questão é válida.
2) Na situação mostrada na
figura seguinte, em que o peso P
se encontra em equilíbrio,
determine a força de tração no fio
preso em B.
97

98. R.: Estando o bloco suspenso em equilíbrio, temos que a componente vertical da
tração no fio preso em B é equivalente ao peso. Assim:
2
T. P
2
Daí: T P. 2
Equações do movimento
Consideremos um ponto material de massa m sobre o qual atuam diversas
forças.
     
m.a m.a 1 m.a 2 m.a 3 m.a 4 m.a5
    
a a 1 a 2 a 3 a 4 a5
Podemos operar com quantidades escalares em vez de vetoriais,
 
decompondo F e a segundo eixos coordenados, escolhidos conforme
as circunstâncias do problema. A seguir, destacamos três sistemas de
coordenadas.
Componentes cartesianas:
Se decompusermos as forças segundo três eixos x, y e z mutuamente
perpendiculares, encontramos, pela aplicação da segunda lei de Newton:
     
( Fx .i Fy . j Fz .k ) m.(ax .i a y . j az .k )
98

99. d 2x
Fx m.a x m.
dt 2
d2y
Fy m.a y m. 2
dt
d 2z
Fz m.a z m. 2
dt
Componentes normal e tangencial
As forças e a aceleração também podem ser apresentadas em termos de suas
componentes nas direções tangente e normal à trajetória. Assim:
 
F m.a
    
F Ft Fn m.a t m.an
  dv 
Ft m.a t m. .it
dt
  v2 
Fn m.a n m. .in
onde é o raio de curvatura da trajetória
99

100. A aceleração normal (ou centrípeta) é, como visto anteriormente, responsável pela
mudança na direção do movimento. A ela está associada a força centrípeta9. Esse
tema voltará a ser tratado quando discutirmos movimento de força central.
Componentes radial e transversal
Assim como utilizamos coordenadas polares para expressar os vetores posição,
velocidade e aceleração no movimento curvilíneo, também as equações gerais do
movimento podem ser apresentadas como:
    
F Fr F m.a r m.a
  d 2r d
2

Fr m.a r m. 2 r. .ir
dt dt
  d2 dr d 
F m.a m. r. 2. . .i
dt 2 dt dt
9 A força centrípeta (normal à trajetória) não é, ao contrário do que muitos imaginam, uma força
exercida por um único e determinado agente. Trata-se, efetivamente, da resultante das forças
atuantes na direção normal à da trajetória, que produz a aceleração centrípeta.
100

101. Quantidade de movimento
Exploremos, um pouco mais, a expressão da segunda lei de Newton.
 
F m.a
 
dv
F m.
dt
Desde que a massa seja constante:
 
d (m.v )
F
dt

A grandeza resultante do produto m.v é, por definição, a quantidade de
 
movimento p da partícula de massa m dotada de velocidade v .
Portanto:
A resultante das forças atuantes sobre um ponto material é igual à variação da
quantidade de movimento por unidade de tempo.
De fato, a formulação original da segunda lei de Newton se expressa por: “A
variação do momento (quantidade de movimento) é proporcional à força atuante e
tem a mesma direção dessa força”. Isso significa que a força é a taxa de variação
temporal da quantidade de movimento.
101

102. Uma restrição a esta nova expressão é que ela não pode ser aplicada diretamente
na solução de problemas de movimento de corpos que ganham ou perdem massa.
Disso, trataremos adiante.

Quando F é igual a zero, também nula é a taxa de variação da quantidade de
movimento. Temos, assim, um princípio importante: o da conservação da
quantidade de movimento (ou momento linear), como será discutido adiante.
Momento angular
Consideremos o ponto material P, indicado na figura seguinte.
  
Ho r (m.v )
 
Chamamos de momento angular H o o produto vetorial do vetor-posição r pela
quantidade de movimento. Assim:
  
i j k

Ho x y z
m.v x m.v y m.v z
Observemos que:
v v.sen
d
v r.
dt
O módulo do vetor momento angular é dado por:
102

103. d
Ho r.m.v.sen m.r 2 .
dt
Com base a segunda lei de Newton, podemos afirmar que a soma dos momentos
das forças atuantes sobre o ponto material, em relação a O (origem do sistema de
referência), é igual à variação, por unidade de tempo, do momento angular do
ponto material em relação a O.
  
dH o dr   dv
(m.v ) r m.
dt dt dt

dH o    
v (m.v ) r (m.a )
dt
   
v (m.v ) 0 , pois os vetores v e m.v têm a mesma direção e sentido (ou
seja, é nulo o ângulo formado entre eles).

dH o  
r ( m.a )
dt

dH o
corresponde à derivada do momento angular em relação ao tempo,
dt
 
equivalente, portanto, ao momento das forças atuantes, isto é, r (m.a ) .

Podemos obter a expressão de F , apresentada anteriormente, a partir dessa
última expressão. Assim:
d
d m.r 2 .
dH o dt d2 dr d
r. F m. r 2 . 2.r. .
dt dt dt 2 dt dt
Portanto:
d2 dr d
F m. r. 2 2. .
dt dt dt
103

104. Sistema referencial inercial
Para que as equações do movimento propostas por Newton sejam aplicáveis, o
sistema de referência não pode ser arbitrário. É necessário que as variáveis do
movimento (posição, velocidade, aceleração) sejam medidas em relação a um
sistema referencial inercial (ou newtoniano). Tal sistema somente pode sofrer
translação com velocidade constante, ou seja, sem aceleração.
A rigor, os eixos do sistema de referência devem ter orientação constante com
relação às estrelas e sua origem deve estar amarrada ao centro de massa do
Sistema Solar ou deslocando-se com velocidade constante em relação a ele.
É aceitável, para a solução de problemas de dinâmica na superfície da terra, que
se adote uma referência solidária ao solo; nesse caso, os erros decorrentes do
movimento do planeta são pequenos e podem ser desprezados. Por outro lado,
em estudos de movimento de satélites e foguetes espaciais, impõe-se, de fato, um
sistema referencial inercial fixo às estrelas.
Referenciais não inerciais podem ser, no entanto, utilizados na prática. Nesse
caso, são introduzidas pseudoforças (ou forças de inércia), dentre as quais podem
ser citadas a força centrífuga (atuante sobre corpo em repouso em relação a
referencial em rotação) e a força de Coriolis (atuante sobre corpo em movimento
em relação a referencial em rotação).
Sistema de partículas
Vamos estender as equações do movimento a um sistema de partículas.
Considere o sistema mostrado na figura seguinte, em que Fi é uma força externa
atuante sobre a partícula i do sistema e fi, uma força interna sobre essa mesma
partícula.
104

105.   
Fi fi mi .ai
  
Fi fi mi .ai

fi 0 , pois as forças entre as partículas aparecem aos pares, no âmbito do
sistema.
 
Assim: Fi mi .ai
 
m.aG mi .ai
 
F m.aG
G denota o centro de massa.
O conceito de centro de gravidade é importante, sobretudo, quando estamos
tratando de corpos extensos (o que será visto num módulo posterior).
 
Por definição: m.rG mi .ri , onde m é a massa total do sistema (todas as
partículas)
Movimento pela ação de força central

Seja um ponto material P sobre o qual atua uma única força F dirigida para um
ponto fixo O, como ilustra a figura seguinte.
Nesse caso, P move-se sob ação de força central, sendo O o centro da força.
Podemos generalizar: uma partícula, numa dada região do espaço, está sujeita a

forças centrais quando cada força F atuante sobre ela em qualquer ponto dessa
região goza das propriedades seguintes:
105

106. a) está orientada segundo a linha que liga o ponto da partícula a um ponto
fixo, que corresponde ao centro das forças;
b) apresenta intensidade (magnitude) numa dependência funcional com a
distância entre o ponto da partícula e o centro das forças.
São exemplos de forças centrais: i) a força gravitacional (atrativa) que atua sobre
um planeta pela presença do Sol; ii) a força elétrica sobre um elétron devido ao
núcleo positivo de um átomo. O movimento planetário e o movimento de veículos
espaciais ao redor da Terra são movimentos sob ação de forças centrais. Um
aspecto que, em geral, caracteriza uma força central é que a sua intensidade varia
inversamente com o quadrado da distância entre a partícula a ela submetida e o
centro dessa força.
Justifica-se, portanto, o estudo particularizado do movimento sob ação de forças
centrais.
Tomemos, como exemplo, o esboço da figura seguinte:
P1, P2 e P3 são pontos de localização da partícula, em diferentes instantes.
  
F1 , F2 e F3 são as forças exercidas na partícula quanto esta se encontra,
respectivamente, nos pontos P1, P2 e P3.
 
Podemos expressar Fi (i=1, 2, 3) em termos do vetor unitário ri associado a
  
cada direção radial OPi . Assim: Fi Fi .ri ( Fi , escalar, é positivo (força
repulsiva) ou negativo (força atrativa)).
106

107. É fácil perceber que a análise desse movimento é mais bem conduzida a partir de
coordenadas polares, anteriormente apresentadas. Assim:
2
d 2r d
Componente radial da força: F m. 2 r.
dt dt
d2 dr d
Componente transversal da força: 0 m. r. 2. .
dt 2 dt dt
Decorre dessa última expressão que:
1 d 2 d
. r . 0
r dt dt
d
r 2. h
dt
onde h é uma constante de integração.
Caracterizemos, então, a trajetória de um ponto material sob a ação de força
central.
As equações obtidas com a aplicação da segunda lei de Newton às componentes
radial e transversal conduzem à definição do momento do ponto material P.
d Ho
Sendo r 2 . h , onde h , temos, pois, as seguintes relações:
dt m
d h
dt r 2
1
d( )
dr dr d h dr
. . h. r
dt d dt r 2 d d
107

108. dr dr 1 1
d( ) d( ) d( ) d2( )
d 2r dt . d h h d h2
. dt . h. r . r
dt 2 d dt r 2
d r2 d d r 2
d 2
Aplicando estas derivadas na expressão de Fr (componente radial da força
central, obtemos:
1
d2( )
r 1 F
d 2 r 1
m.h 2 .( ) 2
r
A equação precedente especifica a trajetória seguida pelo ponto material sob ação

da força central F .

O escalar F, nessa equação, assume valor positivo se a força F é de

aproximação (força de atração) ou valor negativo se F estiver se afastando do
ponto central (força repulsiva).
- A equação da trajetória é obtida integrando-se a equação diferencial
acima para (1/r) em função de ; as constantes de integração são
determinadas com base nas condições iniciais;
- Em caso de aplicação específica, como na mecânica espacial, a
equação diferencial anterior assume aspecto mais bem definido, em
geral, mais simples.
Força centrípeta
A situação mais simples de movimento sob ação de força central é aquela em que
uma partícula descreve movimento circular uniforme. Nesse caso, a força
resultante será orientada para o centro da trajetória (circunferência) e será
responsável unicamente pela variação de direção da velocidade.
108

109.  a aceleração centrípeta é dada por:
 v2 2
a cp .r
r
v2 2
Fcp m.a cp m. m. .r
r
 a velocidade tangencial terá módulo
constante
Observe-se, porém, que, havendo variação no módulo da velocidade tangencial
(nesse caso, não mais movimento circular uniforme), a força resultante deixa de
ser central.
Retornando à componente radial da força, temos:
d 2r d 2
m.( r.( ) ) F
dt 2 dt
dr
0
dt
d 2r
0
dt 2
d
m.r.( ) 2 F
dt
d
dt
m.r. 2 F
2 v2
r. a cp
r
109

110. Aplicações:
Problemas resolvidos:
1) Considere uma pequena esfera de
massa m amarrada a um fio de
comprimento L, posta a girar descrevendo
uma circunferência horizontal com
velocidade constante, como ilustra a figura
seguinte. A máxima tensão suportada pelo
fio é T. Determine: i) a máxima velocidade
permitida para a esfera; ii) o
correspondente ângulo .
 
R.: Sobre a esfera atuam a força peso P e a força de tração T transmitida pelo
fio. A força resultante é centrípeta. Podemos compor as seguintes relações:
T . cos P m.g
m.v 2
T .sen
R
onde R é o raio de curvatura da trajetória descrita pela esfera.
R L.sen
Então:
m.g m.g
cos arccos
T T
m.v 2
T .sen
L.sen
T .L
v .sen
m
110

111. As leis de Kepler
Baseado nas observações realizadas por Tycho Brahe (1546-1601), Johannes
Kepler (1571-1630) apresentou as três leis que governam o movimento de
translação dos planetas. Constituem, portanto, leis empíricas, resultantes de
observações sistemáticas.
De uma maneira geral, a validade das leis de Kepler se estende a quaisquer
corpos que gravitem em torno de outro com massa bem maior. Por exemplo, os
satélites artificiais em torno da Terra.
Primeira lei:
Os planetas descrevem órbitas elípticas em torno do Sol, ocupando este um dos
focos da elipse.
Segunda lei:
O raio vetor que une o Sol a qualquer planeta varre áreas iguais em intervalos de
tempo iguais.
Terceira lei:
O quadrado do período de revolução de um planeta é proporcional à terceira
potência do semi-eixo maior da sua órbita.
A segunda lei de Kepler explica por que
os planetas apresentam maior
velocidade quando se encontram mais
próximos do Sol.
Na figura ao lado, sendo o tempo que o
planeta leva de A até B equivalente ao
tempo que ele leva de C até D, então
as áreas A1 e A2 serão iguais.
111

112. Dizemos, então, que um planeta apresenta velocidade areolar (área varrida por
unidade de tempo) constante.
T2
Pela terceira lei de Kepler, temos: k
R3
onde T é o período de revolução (tempo que o planeta leva para completar uma
volta em torno do Sol) e R o raio médio de sua órbita (aproximadamente circular).
O valor aproximado de k é 3.10-19 s2/m3.
Coube a Newton fazer a demonstração completa das três leis de Kepler, tendo,
ainda, apresentado, em 1686, uma lei que rege a atração mútua entre duas
partículas quaisquer.
Massa atrai massa na razão direta do produto dessas massas e na razão inversa
do quadrado da distância entre elas.
Simbolicamente, esse enunciado pode ser traduzido na expressão seguinte:
m1 .m2
F G
d2
onde G é a constante da gravitação universal10 (No SI, vale 6,67.10-11N.m²/kg²).
Observações:
- a força exercida pela Terra sobre um corpo de massa m, próximo a ele, denomina-se

peso ( P ) e pode ser expresso como o produto da massa do corpo pela aceleração da
 
gravidade g (vetor orientado para o centro da Terra). O módulo de g é dado por:
M
g G.
R2
onde M é a massa da Terra e R, o raio da Terra
  
- os valores de P e de g variam com a altitude (maior altitude, menor g ) e a

latitude do ponto considerado (maior latitude, maior g )
- a aceleração da queda dos corpos na Terra tem a mesma origem que a aceleração
que mantém a Lua em órbita.
10 A determinação experimental de G somente coube a Henry Cavendish, utilizando a balança de
torção, um século após a publicação da teoria de Newton.
112

113. Uma breve dedução das leis de Kepler pode ser encetada a partir da lei da
gravitação de Newton. Consideremos, inicialmente, dois planetas 1 e 2 movendo-
se em órbitas circulares11 em torno do Sol. Sejam as suas massas M1 e M2, os
raios de suas órbitas R1 e R2 e os seus períodos T1 e T2. Pela segunda lei de
Newton:
F1 M 1 .a1
4. 2
a1 .R1
T12
4. 2
F1 M 1. .R1
T12
M S .M 1
F1 G
R12
M S .M 1 4. 2
G M 1. .R1
R12 T12
4. 2 MS
.R1 G.
T12 R12
R13 MS
G.
T12 4. 2
Note-se que a expressão do segundo membro independe da massa do planeta. Se
aplicarmos o mesmo procedimento ao planeta 2, encontramos:
3
R2 MS
G.
T22 4. 2
Ou seja, qualquer que seja o planeta, será constante a razão entre o cubo do raio
da órbita e o quadrado do período de translação do planeta. Assim:
R13 R23
T12 T22
11As órbitas de todos os planetas, exceto Plutão, muito se aproximam de uma circunferência, com o
Sol em seu centro.
113

114. Movimento de satélites
Um satélite em órbita circular em torno do centro da Terra está submetido à
necessária força centrípeta graças à atração gravitacional que Terra exerce sobre
ele. Diferentes alturas de órbitas irão corresponder a diferentes velocidades.
Seja r (= RT + h ; RT: raio da Terra; h: altura do satélite) o raio da órbita do
satélite, temos a seguinte expressão para a força de atração exercida pela Terra:
M T .m
F G.
r2
onde MT é a massa da Terra (supostamente concentrada em seu centro) e m, a
massa do satélite.
Igualando F à força centrípeta, temos:
v2 M T .m
m. G.
r r2
G.M T
Daí: v
r
A altura da órbita do satélite depende de uma série de fatores, mas, sobretudo, de
sua finalidade. Para que a força de resistência do ar não perturbe o seu
movimento, essa altura nunca deve ser inferior a 150km, garantindo-se a ele uma
atmosfera já totalmente rarefeita. Os satélites de comunicação normalmente são
geoestacionários, ou seja, apresentam período igual ao período de rotação da
Terra. Eles operam em órbitas a cerca de 36000km de altura (o seu raio de órbita
é de aproximadamente 42000km (= 36000km + 6000km (raio da Terra)), o que
lhes confere uma velocidade de 10800km/h.
Aplicações:
Problemas resolvidos:
1) Estime a massa da Terra.
R.: Conhecidos o raio da Terra RT , a constante da gravitação G e a aceleração da
gravidade g na superfície da Terra, podemos relacionar:
G.M T
g 2
RT
114

115. 2
g .RT
Assim: MT
G
2) Estime o valor da velocidade horizontal que deve ser comunicada a um corpo
para que ele passe a descrever uma órbita rasante à superfície da Terra.
R. Vamos aplicar a equação da velocidade de um satélite, considerando h nulo, o raio da
órbita (r) será igual ao raio da Terra (RT). Substituindo os valores de G, MT e RT
(conhecidos), chegamos ao valor de v: 28800km/h. Trata-se de um valor teórico, de
improvável confirmação prática, já que essa elevada velocidade implicaria uma imensa
força de resistência do ar.
3) O planeta Marte está a uma distância do Sol 52% maior do que da Terra.
Estime a duração do ano marciano.
R.: Com base na terceira lei de Kepler:
2 3
TM RM
TT2 3
RT
2
TM (1,52.RT ) 3
TT2 RT3
TM (1,52.RT ) 3
3
(aqui, RT denota o raio médio de curvatura da órbita da Terra)
TT RT
Daí se depreende que a duração do ano marciano é cerca de 1,87 maior do que o ano da
Terra, que é de, aproximadamente, 365,25dias.
4) A massa da Lua é cerca de 1,2% da massa da Terra e seu diâmetro é,
aproximadamente, 27% do diâmetro da Terra. Estime o valor da aceleração da
gravidade na superfície da Lua.
R.: Pela lei de Newton da gravitação universal:
G.M L G.M T
gL 2
e gT
RL RT2
2
gL M L .RT
Então, podemos relacionar: 2
gT RL .M T
Portanto, a aceleração da gravidade na superfície da Lua vale, aproximadamente,
0,165.gT.
115

116. Marés oceânicas
Como vimos, o campo gravitacional varia com o inverso do quadrado da distância.
Num corpo extenso (não pontual) deve ser reconhecido que a força originada desse
campo varia entre os pontos desse corpo. Um exemplo está na força exercida pela Lua
sobre a Terra – nas partes da Terra mais próximas da Lua, a força é mais intensa do
que nas partes mais afastadas da Lua.
Comparemos a força sobre uma massa m na face da Terra voltada para a Lua com a
força sobre uma mesma massa m situada, agora, na face oposta. A figura seguinte
esclarece:
A diferença entre essas forças pode assim ser estimada:
M L .m M L .m
F G. G.
(d R) 2 (d R) 2
onde ML é a massa da Lua; R, o raio da Terra e d, a distância entre os centros da
Terra e da Lua.
Desenvolvendo:
G.M L .m. (d R) 2 (d R) 2
F
(d R) 2 .(d R) 2
G.M L .m.d .R 4.G.M L .m.R
F
(d 2 R 2 ) 2 d3
O Sol também exerce força sobre a massa m situada na superfície na Terra. A
magnitude dessa força é, de fato, bem maior do que aquela exercida pela Lua. No
entanto, a diferença calculada acima é muito mais significativa em se tratando da Lua
do que do Sol (isso porque a distância da Terra ao Sol é praticamente a mesma
qualquer que seja o ponto da Terra considerado). Imaginemos, então, a massa m
aludida sendo as águas do mar; temos, nesse caso, o fenômeno das marés.
Assim também se explica por que as marés oceânicas recebem maior influência da
Lua do que do Sol.
116

117. Massa gravitacional e massa inercial
Conceitualmente, as grandezas massa gravitacional e massa inercial não devem
ser confundidas. A primeira é a propriedade de um corpo responsável pela ação
(força) gravitacional que esse corpo exerce sobre outro, como prevê a lei da
gravitação universal. A massa inercial, por outro lado, está relacionada à
resistência à aceleração, ou seja, quanto maior a massa inercial de um corpo,
maior o esforço necessário para alterar o seu estado de equilíbrio, produzindo
aceleração, de acordo com a segunda lei de Newton da dinâmica (comumente,
dizemos que a massa é a medida da inércia de um corpo).
Não raro, essa base conceitual entre as massas gravitacional e inercial é relaxada.
Isso se dá por uma simples razão: experimentalmente, uma é igual à outra. De
fato, a força gravitacional exercida pela Terra sobre um corpo é diretamente
proporcional à massa inercial desse corpo. Decorre daí que, afastados os efeitos
da resistência do ar, todos os corpos próximos à superfície da Terra caem com
igual aceleração (fenômeno de queda livre).
Devemos enfatizar, então, que, embora não haja motivo prático (durante a
resolução de problemas) para se manter a distinção entre as massas gravitacional
e inercial, elas se referem a grandezas físicas diferentes e que a equivalência
entre elas é uma lei experimental, portanto, limitada pela precisão dos
instrumentos de medição. Tal exatidão alcança, no dias atuais, 1 parte em 1012,
sendo, destarte, essa equivalência uma das leis da física mais bem
fundamentadas, oferecendo suporte, inclusive, para a Teoria da Relatividade,
proposta por Albert Einstein.
As limitações das leis de Newton
De acordo com a concepção da Física Clássica, a massa, o tempo e o
comprimento são grandezas absolutas, ou seja, independem do referencial
adotado para medi-las. Esses conceitos passaram por revisão, a partir do início do
século XX: tudo é relativo e depende do referencial. Tal constatação, porém, não
afastou o interesse prático pela Física estruturada no século XVII, ainda hoje
objeto do currículo acadêmico.
De fato, embora ainda úteis para a compreensão de um amplo elenco de
problemas e situações, a leis de Newton não são capazes de descrever todos os
fenômenos conhecidos hoje da mecânica.
Atualmente, as limitações presentes nas leis formuladas por Newton estão bem
identificadas, a partir das teorias da relatividade e da mecânica quântica.
117

118. i. Teoria da Relatividade Especial (ou Relatividade Restrita)
Não podemos extrapolar o uso das leis de Newton para partículas
que se movem com velocidades comparáveis à da luz. Na teoria
relativística, a visão espaço-tempo é claramente não-newtoniana,
podendo ser aplicada em quaisquer circunstâncias (altas ou baixas
velocidades); em baixas velocidades, a dinâmica da relatividade
especial se reduz diretamente às leis de Newton.
ii. Teoria da Relatividade Geral
Não podemos usar as leis de Newton na proximidade de um campo
gravitacional muito forte. A relatividade geral se aplica a campos
gravitacionais fortes e fracos; em campos gravitacionais fracos,
reduz-se às leis de Newton.
iii. Mecânica Quântica
Não podemos empregar as leis de Newton a objetos tão pequenos
quanto o átomo. A mecânica quântica pode ser aplicada a átomos
individuais ou a objetos comuns (com enorme número de átomos); no
caso de objetos comuns, a média dos movimentos aleatórios
previstos para o átomo conduz às leis de Newton.
Apenas à guisa de ilustração, já que este texto atina, precipuamente, a mecânica
clássica, relacionamos, a seguir, algumas das formulações decorrentes da teoria
da relatividade restrita:
i) tempo dilatado ( tD):
tP
tD
2
v
1
c
tP é o tempo próprio, assim denominado o tempo medido por um
relógio que se encontra parado em relação ao local dos eventos.
ii) comprimento contraído ( LC):
2
v
LC LP . 1
c
118

119. LP é o comprimento próprio, assim denominado o comprimento medido
por um observador que se encontra parado em relação ao objeto que
está sendo medido.

iii) cálculo da velocidade relativa ( v R ):

 vA
vB
vR
v .v
1 A2B
c
iv) equação da velocidade de um ponto material partindo do repouso
com aceleração constante:
a.t
v
2
a.t
1
c
v) massa de uma corpo (mo é a massa do corpo quando em repouso):
mo
m
2
v
1
c
vi) energia total de uma partícula (p é a quantidade de movimento):
E2 p 2 .c 2 mo .c 4
2
O leitor pode verificar, facilmente, a aproximação quando as velocidades
envolvidas são bem menores do que a velocidade da luz no vácuo (c), como sói
acontecer em fenômenos típicos do dia-a-dia.
119

120. Diretrizes básicas para a solução de problemas de dinâmica
Não é raro o estudante, mesmo com uma boa compreensão do enunciado das leis
da dinâmica, enfrentar bloqueio mental diante de um problema posto para solução
analítica ou numérica. Também não é incomum encontrar aqueles que, mesmo sem
um sólido entendimento dos princípios que governam determinado fenômeno, sejam
capazes de resolver problemas simplesmente porque já viram outro bastante
parecido, podendo, então, reproduzir as mesmas etapas até alcançar uma solução
ou resultado final. É absolutamente indesejável, para o estudante, a mecanização de
procedimentos. Com efeito, o aluno deve ser estimulado de forma contínua à
reflexão, à crítica, a um raciocínio consistente a cada cena. Há um típico processo de
construção e amadurecimento da aprendizagem que deve ser respeitado. Somente
com o tempo e a vivência, o estudante persistente poderá adquirir sensibilidade e
definir melhor a sua própria metodologia.
Por enquanto, os problemas que envolvem as leis de Newton podem ser resolvidos
com relativa facilidade se obedecidos os passos seguintes:
i) Elaboração de desenhos esquemáticos que retratem, ainda
simbolicamente, o enunciado do problema;
ii) Identificação do(s) corpo(s) (partícula(s)) a ser(em) destacado (a)(s),
ou seja, as partes relevantes do cenário descrito no enunciado do
problema;
iii) Identificação das forças atuantes na(s) partícula(s);
iv) Concepção mental do que seria uma solução razoável (ditada pela
razão e pelo bom-senso);
v) Elaboração do diagrama de forças, diagrama de corpo livre;
vi) Eleição de um sistema de coordenadas de referência;
vii) Identificação e aplicação das leis da física que governam o fenômeno
em questão (no caso da dinâmica da partícula, as leis de Newton);
viii) Verificação dos dados fornecidos (se são consistentes e suficientes
para se alcançar a solução);
ix) Cálculo matemático para resolução das equações nas incógnitas
solicitadas;
x) Confrontação da resposta obtida com aquela preliminarmente
concebida;
xi) Anotação dos aspectos singulares do problema, para compor o elenco
de informações úteis ao enfrentamento de futuros problemas.
120

121. Trabalho e energia
T rabalho é um daqueles conceitos físicos que assumem, na linguagem
coloquial, uma conotação um tanto diferente da que a ciência estabelece. A
rigor, o trabalho pressupõe uma força provocando deslocamento em dado corpo
sobre o qual ela atua. Por exemplo, um bloco sobre uma mesa recebe
lateralmente uma força de intensidade crescente e enquanto a força de atrito
estático máxima não for superada, não haverá deslocamento, daí essa força não
promove trabalho12; por outro lado, mesmo havendo deslocamento (quando a força
aplicada superar a força de atrito estático máxima), a força normal (aplicada ao
bloco pela mesa) não estará realizando trabalho, já que ela atua numa direção
perpendicular à do deslocamento. Efetivamente realiza trabalho a força que
apresenta componente não nula na direção do deslocamento, favorecendo-o ou
não. A rigor, trabalho é uma grandeza sempre associada a uma força: somente
esta pode ser capaz de realizar trabalho. Ou seja: uma pessoa ou uma máquina
não realizam trabalho diretamente, ao contrário do senso comum.
Numa abordagem primária, o aluno pode propor que durante o seu estudo,
no ambiente confortável de uma sala, em que se concentra numa leitura
silenciosa, nenhum trabalho é realizado. Noutra situação, se uma pessoa
apóia em sua mão um certo corpo numa posição fixa, sobre este não haverá
trabalho; no entanto, a pessoa estará “cansada” após algum tempo, como
também “cansado” estará aquele nosso aluno. Afinal, há ou não realização
de trabalho nessas circunstâncias? Se não, como justificar o desgaste físico
experimentado por nossos protagonistas? (Procure refletir para encontrar
uma resposta razoável).
Energia e trabalho são temas fortemente relacionados. Costuma-se dizer que
energia é a capacidade de realização de trabalho. Ou ainda que o trabalho é o
resultado de um processo de transformação de energia.
Vamos procurar esclarecer melhor esses conceitos, a partir da compreensão da
utilidade que a grandeza física trabalho oferece na análise da dinâmica dos
corpos.
12 Numa perspectiva virtual, o trabalho dessa força estaria sendo compensado (anulado) pelo
trabalho (negativo) realizado pela força de atrito. Esta assertiva merece alguns reparos.
121

122. Trabalho realizado por uma força
Define-se trabalho de uma força o produto dessa força pelo deslocamento que ela
produz na sua própria direção.

Em termos vetoriais, se uma força F provoca na partícula um deslocamento

infinitesimal dr , o trabalho (infinitesimal) se expressa por:
 
d F .dr
O trabalho é, portanto, o produto escalar do vetor força pelo vetor deslocamento.
Assim:
d F.ds. cos
Para o caso mais geral, em que a força varia em função da posição, temos:
r2
  s2
1 2 F .dr F . cos .ds
r1 s1
As figuras seguintes ilustram os casos de força constante e de força variável.
122

123. Forças aplicadas a sistemas fixos ou que agem em direção perpendicular ao
deslocamento não realizam trabalho.
Algumas particularizações:
Trabalho de um peso:
d P.dy
B
A B P.dy P. y A P. y B
A
A B P. y
O termo P.y é denominado energia potencial gravitacional. Deve ser observado
que a quantificação da energia potencial gravitacional demanda o estabelecimento
de um plano de nível referencial (datum). Acima desse plano de referência, a
energia potencial é positiva; abaixo, negativa.
No caso mostrado na figura acima, o sinal negativo do trabalho decorre do fato de
que o eixo y foi escolhido para cima.
Trabalho da força exercida por uma mola:
Pela lei de Hooke:
F k .x
d F .dx k .x.dx
x2
1 1
A B k .x.dx .k .x12 2
.k .x 2
x1
2 2
123

124. 1
O termo .k .x 2 é denominado energia potencial elástica.
2
Trabalho de uma força gravitacional:
Pela lei da gravitação universal, duas massas interagem por uma força de campo

F.
M .m
F G.
r2
M .m
d F .dr G. .dr
r2
r2
G.M .m G.M .m G.M .m
A B .dr
r1 r2 r2 r1
Princípio do trabalho e energia
Esse princípio é empregado na solução de problemas que envolvem velocidade,
força e deslocamento.
Com base na segunda lei de Newton:
Ft m.at
Ft é a componente da força na direção tangente à da trajetória (portanto, na
direção do deslocamento).
dv
Ft m.
dt
ds dv
Ft m. .
dt ds
dv
Ft m.v.
ds
Ft .ds m.v.dv
124

125. Se várias forças atuam sobre a partícula, temos:
s2 v2
Ft .ds m.v.dv
s1 v1
s2
1 2 1
Ft .ds .m.v 2 .m.v12
s1
2 2
1 2 1
U1 2 .m.v 2 .m.v12
2 2
1
O termo .m.v 2 é denominado energia cinética.
2
Ec1 Ep1 2 Ec2
A energia cinética final de uma partícula ao mover-se de uma posição inicial a uma
posição final é igual à energia cinética inicial dessa partícula somada ao trabalho
realizado por todas as forças que atuam sobre ela durante o deslocamento.
Observações:
- trabalho e energia são grandezas escalares; portanto, as operações de
soma devem ser algébricas ordinárias;
- a energia cinética é sempre uma grandeza positiva;
- a energia cinética de um ponto material representa a capacidade de
realizar trabalho associada à velocidade desse ponto material;
- a aplicação do princípio do trabalho e energia simplifica sobremaneira a
solução de muitos problemas envolvendo forças, deslocamentos e
velocidades. No entanto, o método do trabalho e energia não é aplicável à
determinação direta da aceleração.
Aplicações:
Problemas resolvidos:
1) Sobre uma partícula atua a força variável, em N, expressa por
  
F 1,5.x.i 3. j (com x em metros). Determine o trabalho realizado por essa
125

126.   
força quando a partícula se desloca da posição r1 2.i 3. j para a posição
  
r2 4.i 3. j .
R.: O vetor deslocamento, que corresponde à diferença entre os vetores-posição final e
inicial, é obtido por:
       
r2 r1 r2 ( r1 ) 4.i 3. j ( 2.i 3. j )
  
r2 r1 6.i
Operando escalarmente os vetores força e deslocamento, obtemos:
r2
  4 3
1 2 F .dr 1,5.x.dx 3.dy
r1 2 3
4
x2 3
1 2 1,5. 3. y 3
2 2
1 2 9,0 J
2) O bloco de massa 2kg mostrado na figura seguinte apresenta velocidade de
4m/s ao passar pelo ponto A. O coeficiente de atrito cinético entre o plano
inclinado 30º e o bloco vale 0,25. Determine a velocidade desse bloco ao passar
pelo ponto B, distante 5m de A.
R.: As duas forças que realizam trabalho são a força peso e a força de atrito. O trabalho
total (equivalente à variação da energia cinética) é obtido de:
A B P Fat
o
P m.g.h.sen30 2.10 .5.0,5 50 ,0 J
o
Fat m.g. cos30 . c 2.10.0,87.0,25.5 21,8J
126

127. Fazendo Ec , temos:
1 2 1 2
A B .m.v B .m.v A
2 2
Substituindo os valores:
1 2 1
28,2 .2.v B .2.4 2
2 2
Daí: v B 3,5m / s
A diferença entre a energia cinética em A e a energia cinética em B corresponde à energia
mecânica dissipada pelo atrito (possivelmente sob a forma de calor).
3) Sobre uma caixa de massa 8kg, inicialmente em repouso, aplicam-se as forças
 
F1 e F2 , de módulos 30N e 40N, respectivamente, como mostrado na figura
seguinte. O coeficiente de atrito cinético entre a caixa e a superfície de apoio vale
0,2. Determine a distância a ser percorrida pela caixa até que ela atinja a
velocidade de 4m/s.
R.: Podemos compor o seguinte diagrama de corpo isolado:
 
Das forças atuantes, somente F1 , F2 e a força de atrito realizam trabalho.
Expressemos, então, o trabalho de cada uma dessas forças:
F1 F1. cos30o.d 30.0,87.d
127

128. F2 F2 . cos25o.d 40.0,91.d
Fat Fat .d m.g . c .d 8.10 .0,2.d
O trabalho total (soma algébrica dos trabalhos individuais) é:
F1 F2 Fat 46 ,5.d
O trabalho total equivale à variação de energia cinética sofrida pelo bloco. Portanto:
1
46,5.d .8.4 2 d 1,38m
2
Sistema de partículas
Quando um problema envolve dois ou mais pontos materiais, cada ponto material
pode ser considerado separadamente e o princípio do trabalho e energia é
aplicável a cada ponto material. Assim, para um sistema de partículas:
si 2 si 2
1 1
.mi .vi21 Fi t .ds f i t .ds .mi .vi22
2 si 1 si 1
2
si 2 si 2
1 1
.mi .vi2
1 Fi t .ds f i t .ds .mi .vi22
2 si1 si1
2
Potência
Define-se a grandeza escalar potência (P) como a quantidade de trabalho
realizado numa unidade de tempo.
Se uma máquina realiza trabalho d num tempo dt , então a potência se
expressa por:    dr
d F .dr
P F.
dt dt dt

P F .v
Portanto, a potência é o produto escalar dos vetores força e velocidade.
128

129. 
Conhecidas a força F e a velocidade do ponto de aplicação dessa força, a
potência pode ser determinada pelo produto do módulo da força pela componente
da velocidade na direção da força. Assim:
P F.v. cos
 
onde é o ângulo formado entre os vetores F e v .
No SI, a unidade básica de potência é o watt (W), equivalente a
1W 1J / s 1N.m / s
Retomando a expressão do trabalho, temos:
   dr 
d 
d F .dr P F. F .v
dt dt
 
dv  d 1  2 dEC
P F .v m. .dv .m.v
dt dt 2 dt
Portanto, no movimento de uma partícula sob a ação de uma forca, a potência
representa a taxa de variação temporal da energia cinética da partícula.
Particularmente em se tratando de força conservativa, vale a relação:
dU
P
dt
onde U denota a energia potencial da partícula.
Aplicações:
Problemas resolvidos:
1) Um pacote de 100kg é transportado do
chão até uma prateleira a 6m de altura, por
uma empilhadeira elétrica. O gráfico seguinte
ilustra a altura do pacote em relação ao
tempo. Determine a potência aplicada ao
pacote pela empilhadeira.
129

130. R.: Do gráfico, extrai-se a velocidade: 0,3m/s. A potência pode, então ser obtida
simplesmente multiplicando-se a força a ser aplicada (equivalente ao peso, já que a
resultante das forças sobre o pacote deve ser nula) pela velocidade. Assim:
P F .v 100.10.0,3
P 300W
2) Um automóvel acelera de 0 a 100km/h em 8s. Admitindo que a potência do
motor seja constante, determine o intervalo de tempo que o carro leva para
acelerar de 80km/h a 120km/h.
R.: A energia cinética varia Ec no intervalo de tempo t , e assim definimos a potência
média:
Ec
P
t
Sendo constante a potência do motor, temos as seguintes relações:
1 1
.m.v12f .m.v12i
t1 Ec1 2 2
t2 Ec2 1 2 1 2
.m.v2 f .m.v2i
2 2
t1 v12f v12i
2 2
t2 v2 f v 2i
Onde t1 e t 2 são, respectivamente, os intervalos de tempo demandados para as
variações Ec1 e Ec 2 de energia cinética.
Então, substituindo os valores, encontramos:
8 1002 0 2
t2 1202 80 2
t 2 6,4s
3) Considere a situação mostrada na figura seguinte, em que um bloco é puxado
 
para a direita por uma força F , sobre uma superfície rugosa. A velocidade v é

mantida constante e o bloco exibe um deslocamento s , entre os pontos A e B.
Pela aplicação do princípio do trabalho e energia:
130

131. 1 1
.m.v 2 F .s c .FN .s .m.v 2
2 2
Esclareça o seguinte paradoxo aparente: A equação acima é satisfeita se F.s for
equivalente a c .FN . Então, pode-se afirmar que o trabalho realizado pela força

de atrito de deslizamento corresponde ao produto da força F pelo deslocamento
s. Portanto, uma certa quantidade de energia é “criada”, já que durante o
deslocamento as superfícies em contato são aquecidas (liberação de calor).
R.: Devemos reconhecer que o bloco e a superfície horizontal são deformáveis (portanto,
não rígidas). Quando o bloco desliza sobre o plano horizontal da figura, as reentrâncias
(dentes, na figura acima) se deformam (podem vibrar ou até quebrar-se). Assim, as forças
de atrito são um pouco deslocadas, devido às deformações localizadas. Em qualquer
instante, a resultante de todas as forças de atrito praticamente não muda, sendo igual a
c .FN . Ocorre, porém, que o deslocamento real de c .FN não coincide como o

deslocamento s da força aplicada F . Na verdade, s’ é menor do que s; portanto, o
trabalho externo realizado pela força de atrito resultante será c .FN .s ' (e não
c .FN .s ). O aumento de energia interna (associada ao aumento de temperatura do
bloco) será equivalente à diferença desses trabalhos, ou seja: c .FN .( s s' ) .
131

132. Energia cinética e Relatividade
A expressão anteriormente apresentada para a energia cinética não se aplica ao
caso de partículas com velocidades comparáveis à da luz. Nessa circunstância, a
equação é a seguinte:
1
Ec mo .c 2 . 1
2
1 v/c
Para baixas velocidades, as expressões da mecânica newtoniana e da mecânica
relativística revelam-se equivalentes. Basta considerar a seguinte aproximação
matemática, válida quando v é muito menor do que c :
1 v2
1
v
2 c2
1
c
Por outro lado, para velocidades elevadas, os resultados oferecidos pelas duas
equações diferem significativamente entre si. Novamente, cabe enfatizar: a
expressão sempre correta (até prova em contrário!) é a proposta pela Teoria da
Relatividade de Einstein.
Um critério de validade da mecânica newtoniana pode, então, ser apresentado em
termos da energia da partícula. A proposta clássica (de Newton) é aceitável desde
que a velocidade da partícula seja muito menor do que a velocidade da luz,
significando dizer que, nesse caso, a energia cinética da partícula é muito menor
do que a sua energia de repouso.
1 1 v2 1 v2
Ec .mo .v 2 .mo .c 2 . 2 .E o . 2
2 2 c 2 c
onde E o mo .c 2 , ou seja, a energia de repouso da partícula. Assim:
v 2.Ec
c Eo
132

133. Leis de conservação
A s leis de conservação figuram entre as mais úteis e poderosas da Física. Sua
apresentação básica retrata, em geral, um sistema de partículas
completamente isolado das influências externas – à medida que as partículas que
integram esse sistema se movimentam e interagem, há uma certa propriedade do
sistema que se mantém inalterada. Assim, podemos destacar três leis de
conservação na natureza:
i. conservação da energia
ii. conservação do momento linear
iii. conservação do momento angular
Conservação da energia
A idealização de uma entidade como a energia constitui um dos grandes
“achados” da ciência natural. Isso porque, não obstante a diversidade de modos
em que se apresenta, a energia total do Universo não muda em termos de
quantidade. As modalidades energéticas são, via de regra, intercambiáveis, o que
se mostra consistente com a diversidade de fenômenos naturais conhecidos. O
princípio da conservação da energia (ou princípio de Helmholtz) assegura que a
energia não pode ser criada nem destruída, mas, apenas, transformada de uma
espécie em outra. Isso significa que a quantidade de energia de uma determinada
espécie que desaparece deve ser equivalente à quantidade de energia que
aparece, de outra ou outras espécies.
A conservação da energia é um princípio amplo, do qual se desconhece qualquer
violação na natureza. Porém, aqui discutiremos um caso particular dessa
conservação, aplicado especialmente à mecânica.
Forças conservativas
Uma força é dita conservativa quando o trabalho por ela realizado, ao mover uma
partícula entre duas posições, não depender da trajetória, isto é, assumir o mesmo
valor o trabalho qualquer que seja o caminho adotado no movimento.
São exemplos de forças conservativas, o peso e a força elástica de uma mola.
Alguma modalidade de energia potencial sempre estará associada a uma força
conservativa.
Consideremos um deslocamento infinitesimal ao longo da trajetória, entre o ponto
(x,y,z) e (x+dx,y+dy,z+dz). A variação infinitesimal da função potencial será:
133

134. dU V ( x, y, z ) V ( x dx, y dy, z dz)
dU dV ( x, y, z )
 
dU F .dr
     
dU ( Fx .i Fy . j Fz .k ).(dx.i dy. j dz.k )
dU Fx .dx Fy .dy Fz .dz
V V V
Fx .dx Fy .dy Fz .dz .dx .dy .dz
x y z
V ; Fy V ; Fz V
Fx
x y z
Portanto,
 V  V  V 
F .i .j .k
x y z

Ou seja, uma força F é conservativa se for possível identificar uma grandeza
escalar V (função da posição) tal que a expressão acima se confirme. Essa
relação constitui, com efeito, um critério matemático para se verificar o caráter

conservativo de uma força F .
Aplicações:
Problemas resolvidos:
1) Analise o caráter conservativo das seguintes forças, cujas intensidades são
expressas em N e as posições x e y expressas em metros:
  
i) F1 10 .( y.i x. j )
  
ii) F2 10 .( y.i x. j )
R.: Se a força é conservativa, o trabalho por ela realizado independe por percurso adotado
entre dois pontos. Portanto, nesse caso, ao realizar um caminho fechado (ponto de partida
coincidente com o ponto de chegada), o trabalho é nulo. Tomemos, por exemplo, o

seguinte “caminho” a ser seguido pela força F.
134

135.   
Determinando o trabalho realizado pela força F1 10 .( y.i x. j ) , entre os pontos de
coordenadas (0,0), (1,0), (1,1) e (0,1) (caminho fechado da figura), encontramos:
1 1 0 0
10. y .dx ( 10.x).dy 10. y.dx 10.x.dy
0 0 1 1
1 1 0 0
0.dx ( 10.1).dy 10.1.dx 0.dy
0 0 1 1
1 0
0 10. y 0 10.x) 1 0
20J

Portanto, a força F2 é, seguramente, não-conservativa.
  
Por outro lado, o trabalho realizado pela força F2 10 .( y.i x. j ) , entre os mesmos
pontos de coordenadas (0,0), (1,0), (1,1) e (0,1) (caminho fechado da figura), vale:
1 1 0 0
10. y.dx 10.x.dy 10. y.dx 10.x.dy
0 0 1 1
1 1 0 0
0.dx 10.1.dy 10.1.dx 0.dy
0 0 1 1
1 0
0 10. y 0 10.x 1 0
0

Isso permite, por enquanto, apenas admitir a possibilidade de a força F2 ser conservativa.

Para confirmar esse caráter de F2 , é necessário que encontrar a função U ( x, y) de tal

forma que F2 gradU .
135

136. Com efeito, podemos identificar a função potencial U ( x, y) 10.x. y que atende a

essa condição. Isso garante que a força F2 é, de fato, conservativa. O mesmo não ocorre

com a força F1 .
2) Considere uma partícula movendo-se ao longo da direção x submetida à força
F ( x) a.x b.x 2 , onde a e b são constantes. Encontre a expressão da
energia potencial U(x), sendo U(0)=0.
dU ( x)
R.: Devemos encontrar a função U(x) (potencial) tal que F ( x)
dx
dU ( x) F ( x).dx
x x
U ( x) U (0) F ( x).dx a.x b.x 2 .dx
0 0
x x
U ( x) a. x.dx b. x 2 .dx
0 0
2 x x
x x3
U ( x) a. b.
2 0
3 0
2 3
x x
Daí: U ( x) a. b.
2 3
Conservação da energia mecânica
Como vimos, o trabalho realizado pelas forças conservativas pode ser expresso
como a diferença das energias potenciais. Então, no caso mais geral, em que uma
partícula está submetida a um sistema de forças conservativas e não-
conservativas, a aplicação do princípio do trabalho e energia resulta em:
Ec1 Ep não cons Ec2
Ec1 Ep1 não cons Ec 2 Ep 2
Sendo nulo o trabalho realizado pelas forças não-conservativas, haverá
conservação da energia mecânica, o que permite escrever:
Ec1 Ep1 Ec2 Ep2
136

137. Esta última expressão traduz a conservação da energia mecânica: durante o
movimento, a soma das energias cinética e potencial da partícula não se altera.
Nesse caso, somente poderá ocorrer transformação de energia cinética em
energia potencial e vice-versa.
dE M dEc dEp
0
dt dt dt
No caso particular do movimento unidimensional, podemos escrever:
1
d .m.v 2
dEc 2 dv
m.v. m.v.a Fx .v
dt dt dt
dEp dEp dx dEp
. .v
dt dx dt dx
dEp
Fx .v .v 0
dx
dEp
Fx
dx
A ação de forças conservativas sobre um sistema é igual a menos a derivada da
energia potencial do sistema.
Sistema de partículas
Estando um sistema de partículas submetido apenas a forças conservativas,
temos, entre os pontos 1 e 2:
Ec1 U1 2 Ec2
Ec1 Ep1 Ec2 Ep2
137

138. Ec Ep cons tan te
Observação: Apenas problemas que envolvem sistemas de forças conservativas (peso,
molas) podem ser resolvidos com base no teorema da conservação da energia mecânica.
Forças de atrito e de resistência ao arrasto, que dependem da velocidade e da aceleração,
são não-conservativas.
Força central
Em capítulo anterior, caracterizamos o movimento sob ação de força central.
Determinemos, agora, o trabalho realizado por uma força central quando a
partícula é deslocada entre dois pontos dessa região P’ e P”, por um caminho C.
A força que atua na partícula num

ponto qualquer do percurso é F .
Então:
(C )
P"
 
P ' P" F .dl
P'
   
F .dl F (r ).r .dl

dl . cos dr

O P' r '

O P" r"
r"
(C )
P ' P" F (r ).dr
r'
Esta última expressão mostra que o trabalho P ' P" depende apenas dos pontos
(C )
inicial e final, P’ e P”, ou seja, é independente do caminho adotado. Isso significa
que:
Toda força central é conservativa
138

139. Podemos, a partir dessa constatação, expressar o trabalho em termos da
variação de uma energia potencial U. Assim:
U ( P" ) U ( P' ) P' P"
r"
U ( r" ) U ( r ' ) F (r ).dr
r'
Se definirmos, arbitrariamente, o valor do potencial no ponto central, obtemos que
a energia potencial da partícula em qualquer ponto da região depende somente da
distância da partícula ao centro das forças. Ademais, as superfícies eqüipotenciais
são esferas concêntricas ao centro das forças.

Conseqüentemente, a força central F , sendo força conservativa, pode ser
expressa em termos do gradiente desse potencial. Assim:

F gradU

No caso particular do campo gravitacional uniforme (campo gravitacional g ,
próximo à Terra), temos:
U ( x, y, z ) m.g.z
 U  
F gradU .k m.g.k
z
Aplicações:
Problemas resolvidos:
1) Considere um corpo de massa m abandonado de uma altura h em relação ao
solo. Aplicando da conservação da energia mecânica e desprezando a resistência
do ar, determine a velocidade com que esse corpo atinge o solo.
R.: A energia potencial gravitacional somada à energia cinética permanece inalterada
durante o movimento. Então, adotando plano de referência no nível do solo, podemos
escrever:
1 2 1
m.g.ho .m.vo m.g.h f .m.v 2
f
2 2
1
m.g.h .m.v 2
f
2
139

140. Daí: vf 2.g.h
Note-se que esse resultado é compatível com aquele obtido pelas equações da
cinemática.
2) Considere um corpo de massa m arremessado verticalmente para cima com
velocidade v. Aplicando da conservação da energia mecânica e desprezando a
resistência do ar, determine a altura máxima atingida por esse corpo.
R.: A altura máxima será alcançada quando toda a energia cinética conferida inicialmente
ao corpo (no arremesso) tiver sido convertida em energia potencial gravitacional. Assim:
1
.m.v 2 m.g.hmáx
2
v2
hmáx
2. g
Note-se que esse resultado é compatível com aquele obtido pelas equações da
cinemática.
3) Na situação mostrada na figura
seguinte, um bloco de massa m
comprime x uma mola de
constante elástica k, após o que é
solto. Encontre a expressão da
velocidade desse bloco ao passar
por um ponto qualquer ao longo
da trajetória.
R.: Neste caso, temos três modalidades de energia mecânica envolvidas: energia potencial
gravitacional, energia potencial elástica e energia cinética. Inicialmente, no ponto A, com
o bloco parado e a mola comprimida, há apenas energia potencial elástica, se adotarmos o
plano de referência no nível mais baixo da trajetória. Quando a mola é liberada,
gradativamente a energia potencial elástica converte-se em energia cinética e daí em
energia potencial gravitacional. No ponto B (mais alto da trajetória), toda a energia
mecânica está sob a forma de energia potencial gravitacional.
1
.k .x 2 m.g.h
2
140

141. Em qualquer ponto da trajetória (altura h’), temos o mesmo valor total para a energia
mecânica. Assim, podemos determinar a velocidade do bloco nesse ponto:
1 1
.k.x 2 m.g.h' .m.v 2
2 2
k .x 2
v 2.g.h'
m
4) Considere um brinquedo, conforme ilustra a figura seguinte. Um leve toque é
dado ao carrinho no ponto A, que inicia seu deslocamento à velocidade nula,
deslizando no trilho sem atrito e cumprindo um loop circular de raio R. A altura h,
do ponto A, é mínima para que seja possível o loop sem a perda de contato com
os trilhos. Determine: i) o valor de h em função de R; ii) a força que o trilho exerce
sobre o carrinho no ponto B.
R.: O carrinho desenvolve movimento variado, sem que haja qualquer dissipação de
energia mecânica (desprezam-se, aqui, o atrito e a resistência do ar). Assim, durante todo
o percurso, serão intercambiadas as energias cinética e potencial, porém a soma total
dessas energias não se altera.
Aplicado aos pontos A e B, o princípio da conservação da energia mecânica resulta:
EM A EM B
EC A E PA ECB E PB
1 2 1 2
.m.v A m.g.h .m.v B m.g.2.R
2 2
1 2
g.h .v B g.2.R
2
Para que o carrinho não perca o contato com os trilhos, devemos impor:
Fcp m.g (peso como força centrípeta)
141

142. 2
m.v B
m.g
R
vB g.R
Retomando a expressão da conservação da energia mecânica:
1
g.h .g.R g.2.R
2
5
Daí: h .R
2
Nessa situação limite, é nula a força que o trilho exerce sobre o carrinho em B. A força
centrípeta, responsável por manter a trajetória curvilínea, é devida, nesse caso,
exclusivamente à força peso.
Conservação do momento linear
Consideremos um sistema de duas partículas que interagem entre si através de
  
forças de contato; sejam p1 e p 2 os momentos lineares dessas partículas F1( 2)

a força sobre a partícula 1 devido à partícula 2 e F2(1) a força de 2 sobre 1.
Podemos expressar:
 
dp1
F1( 2)
dt
 
dp 2
F2(1)
dt

dP  
F1( 2 ) F2 (1)
dt
 
F1( 2) e F2(1) são forças de ação e reação (mesmo módulo, mesma direção e
sentidos contrários). Assim: 
dP
0
dt
142

143. Observe-se que a expressão acima não significa que as forças de ação e reação
se anulem (isso, de fato, não ocorre, pois essas forças atuam sobre corpos
distintos).
Se sobre as partículas que integram o sistema em análise atuam forças externas,
além das forças interativas internas, podemos escrever:
  
dp1
F1( 2) F1( ext)
dt
  
dp 2
F2(1) F2( ext)
 dt
       
dP dp1 dp 2
F1( 2) F2(1) F1( ext) F2( ext) F1( ext) F2( ext)
dt dt dt
Se a soma das forças externas que atuam sobre um sistema for nula, a derivada
do momento linear em relação ao tempo também será nula, significando que o
momento linear se mantém inalterado. Nesse caso:

dP 
0 P constante
dt
A lei da conservação do momento linear pode ser assim enunciada: quando a
resultante das forças externas que atuam num sistema de partículas for nula, o
vetor momento linear total do sistema permanece constante.
A condição necessária e suficiente para que o momento total de um sistema de
partículas se conserve é que a resultante das forças externas aplicadas ao
sistema seja nula.
O momento linear total de um sistema pode mudar somente se forças externas
atuarem sobre ele. Havendo somente forças internas, estas, por se
apresentarem aos pares, iguais e opostas (terceira lei de Newton), produzem
variações no momento linear também iguais e opostas, que se cancelarão
mutuamente.
Consideremos um sistema formado por várias partículas, de massas m i que se

encontram, no instante t, em posições definidas pelos vetores ri . Essas partículas
143

144.  
interagem entre si Fi ( j ) e também estão sujeitas a forças externas Fi (ext) . Se as
forças internas satisfazem ao princípio da ação e reação, temos:
 
Fi ( j ) F j (i ) 0 . Assim, aplicando a segunda lei de Newton a cada partícula do
sistema, encontramos:

d 2 r1    
m1 . 2 F1( 2 ) F1( 3) ... F1( N ) F1ext
dt
    
d 2 r2
m2 . 2 F2 (1) F2 ( 3) ... F2 ( N ) F2ext
dt
...
     ext
d 2 rN
mN . 2 FN ( 2 ) FN ( 3) ... FN ( N 1) FN
dt
  
d 2 ri
ou, abreviadamente: mi . 2 Fi ( j ) Fi ext
dt j( j i)
Assim, agrupando todas as partículas:
  
d 2 ri d2 
mi . 2 mi .ri Fi ( j ) Fi ext
i dt dt 2 i i j i
A soma vetorial de todas as forças internas é nula. Assim, a expressão acima fica:

d 2 R  ext
M. 2 F
dt

onde M é a massa total do sistema e R é o vetor-posição do centro de massa,
dado por:
 1 
R . mi .ri
M i
144

145. Pode ser demonstrado que o centro de massa do sistema de partículas se move

como se o momento total P do sistema estivesse concentrado nele.
Assim:
 
P mi .V
i

 dR
onde V é a velocidade do centro de massa.
dt
O princípio da conservação do momento linear leva a uma generalização da lei a
inércia: se a resultante das forças externas que atuam sobre o sistema é nula, o
centro de massa desse sistema permanece em repouso ou em movimento
retilíneo uniforme. Decorre desse princípio que um sistema não pode deslocar
aceleradamente o seu centro de massa sob a ação unicamente de forças internas.
A lei da conservação do momento linear pode ser aplicada a uma grande
variedade de situações físicas, não se conhecendo exceção à sua validade.
Essa lei permanece válida mesmo nos domínios relativístico e quântico.
Podemos escrever, então:
 
mi .(vi )1 mi .(vi ) 2
A lei de conservação do momento linear constitui uma útil ferramenta para a
análise de colisões. Isso porque o momento linear total imediatamente antes do
choque é igual ao momento linear total imediatamente após o choque. Mesmo
havendo dissipação de energia durante a colisão, na forma de calor, por exemplo,
o momento linear do sistema permanece inalterado. Exploraremos melhor esse
tema no próximo capítulo.
Conservação do momento angular
Seja uma partícula P de massa m em movimento em relação a um sistema de

referência inercial (reveja a figura da página 102). O momento angular H o em
145

146. relação à origem do sistema é definido como o momento do vetor quantidade de
 
movimento ( p m.v ) em relação a O. Assim:
  
Ho r (m.v )
 
Esse vetor é perpendicular ao plano que contém r e m.v . Seu módulo vale:
 
H o r.m.vsen , sendo o ângulo entre r e m.v .

As componentes de H o são:
Hox m.( y.v z z.v y )
Ho y m.(z.v x x.v z )
Hoz m.( x.v y y.v x )

Se calcularmos a derivada de H o em relação ao tempo, obtemos:
  
dH o dr   dv    
(m.v ) r (m. ) v (m.v ) r (m.a )
dt dt dt
 
Na expressão acima, v e m.v são paralelos, logo a expressão se reduz a

dH o  
r ( m.a )
dt
   
Pela segunda lei de Newton, temos que F m.a . Assim, r F

corresponde a (soma dos momentos (torques) em relação a O das forças
atuantes sobre a partícula). Portanto, podemos escrever:

 dH o
dt
146

147. Ou seja, a soma dos momentos (torques) em relação a O das forças que atuam
sobre a partícula equivale à variação, na unidade de tempo, do momento angular
da partícula em relação a O. Esta é considerada a lei fundamental da dinâmica de
 
rotações. (Em geral, o momento angular H o e o momento (torque) dependem
do ponto O (origem do sistema de referência)).
Uma conseqüência imediata da relação obtida é a lei da conservação do momento
angular de uma partícula. Assim, se o torque sobre uma partícula em relação a um
ponto se anula, o momento angular da partícula em relação a esse ponto se
mantém inalterado (ou seja, conservam-se o módulo, a direção e o sentido do

vetor H o ).
Um caso particular disso é encontrado no movimento de uma partícula livre (força
resultante nula); ela descreve movimento retilíneo uniforme, logo preservando seu

vetor H o . Outro caso particular importante é o de partícula sujeita a forças
centrais. Neste caso, o torque em relação ao centro de forças é nulo, logo o
momento angular de uma partícula sujeita a forças centrais em relação ao centro
de forças se conserva; decorre daí que o movimento é necessariamente plano.
Se considerarmos, agora, um sistema composto de várias partículas de massa
 
m i e velocidade v i , podemos determinar o momento angular total como:
  
Ho r i (m.vi )
i

dP  
F ( ext) Fi ( ext) , pois a resultante das forças internas se anula
dt i
(terceira lei de Newton)
  
dH o d   dri   dvi
( mi .ri vi ) mi . vi mi .ri
dt dt i i dt i dt
     
mi .vi vi mi .ri ai mi .ri ai
i i i
147

148. Se o referencial é inercial, podemos aplicar a segunda lei de Newton e obter:
   
mi .ai Fi (ext) Fi ( j ) , onde Fi ( j ) é a força interna sobre a partícula i
j, j i
devido à partícula j. Assim:

dH o    
ri Fi ( ext) ri Fi ( j )
dt i i j (i j )
O segundo termo do segundo membro é nulo (a resultante dos torques internos é
nula). Logo:

dH o    (ext)  (ext)
ri Fi (ext) i
dt i i
Para um sistema de partículas, a lei fundamental da dinâmica das rotações
tem o seguinte enunciado: a taxa de variação com o tempo do momento
angular total do sistema em relação a um ponto O (num referencial inercial) é
igual à resultante de todos os torques externos em relação a O que atuam
sobre o sistema.
A lei da conservação do momento angular para qualquer sistema de partículas
decorre da lei fundamental da dinâmica das rotações.
 (ext) 
0 Ho cons tan te
Se a resultante dos torques externos em relação a um dado ponto se anula, o
momento angular do sistema em relação a esse ponto se conserva. Isso também
vale para sistema isolado; neste caso, o torque é nulo em relação a qualquer
ponto do espaço, logo o momento angular em relação a qualquer ponto se
conserva.
Quando uma partícula está sujeita a forças centrais, o momento angular se
conserva em relação ao centro de forças (por exemplo, o momento angular orbital
da Terra em torno do Sol se conserva, pois a força gravitacional é central).
148

149. Como se trata de uma lei de conservação vetorial, ela pode ser aplicada em
relação a cada eixo de referência. Se uma dada componente do torque resultante
se anula, a componente correspondente do momento angular total se conserva,
independentemente do que ocorra com as demais componentes.
O princípio da conservação do momento angular ajuda a entender uma diversidade de
processos físicos, por exemplo: movimento de acrobatas, mergulhadores, dançarinas de
balé e a condensação das galáxias.
Aplicação das leis de conservação – mecânica espacial
Como vimos, quando um ponto material se desloca sob a ação de força central, o
princípio da conservação do momento angular e o princípio da conservação da
energia facilitam bastante a análise do movimento.

Seja F uma força central. A ela, então, podemos associar uma energia potencial.
A energia total do ponto material é constante e equivale ao somatório das energias
cinética e potencial.
Analisemos o caso de um veículo espacial de massa m que se desloca sob a ação
da força gravitacional da Terra, supondo que ele inicia seu vôo livre no ponto Po

distante ro do centro da Terra, com velocidade v o , que forma ângulo o com o

vetor-posição ro .
Pelo princípio da conservação do momento angular, temos:
ro .m.vo . sen o r.m.v. sen
Esta equação pode, então, ser utilizada na determinação do ângulo . Por outro lado,
fazendo-se =90º , podemos determinar os valores máximo e mínimo de r.
Pelo princípio da conservação da energia, temos:
1 2 G.M .m 1 G.M .m
.m.vo .m.v 2
2 ro 2 r
onde M é a massa da Terra.
A equação acima pode ser empregada na determinação da velocidade (v) no ponto P,
desde que se conheça a distância r.
149

150. A aplicação dos princípios da conservação de energia e da conservação do
momento angular permite uma formulação mais fundamental dos problemas
de mecânica em que está presente força central (conservativa), como na
mecânica espacial.

Forças centrais não produzem torque (momento da força) ( ) em relação ao
centro das forças, já que sua linha de ação sempre passa por esse ponto central.
O momento angular de uma partícula sujeita a forças centrais em relação ao
centro das forças se conserva. Este é, com efeito, o enunciado do princípio de
conservação do momento angular.
    
r F r ( F (r ).ri )
 
r // ri

0
Isso implica, então, que o movimento produzido por forças centrais é plano. Isto é,
a partícula sob ação de forças centrais descreve órbita que permanece sempre no
mesmo plano. A figura seguinte esclarece.
 
Sendo ro e v o , respectivamente, os vetores posição inicial e velocidade inicial da
  
partícula de massa m, o momento angular inicial, H o , é o vetor m.ro v o , que,
conforme definição da álgebra vetorial, é perpendicular ao plano definido pelos
  
vetores ro e v o . Tendo em vista que o momento angular (H ) não se altera
 
durante o movimento, sendo sempre H o , ainda que os vetores posição r e
150

151. 
velocidade v possam, individualmente, variar. Ora, desse modo, considerando
 
que dois vetores definem apenas um plano, r e v mantêm-se sempre num
mesmo plano de órbita.
Seja, agora, na figura seguinte, um segmento infinitesimal da trajetória

(correspondente a um diferencial de deslocamento ds ), num dado ponto P. O

vetor r , nesse deslocamento, varre o triângulo hachurado, de área
1   
dA . r ds (ou seja, a metade da área do paralelogramo definido por r e
 2
ds ).
Se calcularmos a taxa de variação dessa área no tempo, encontramos uma
grandeza denominada velocidade areolar. Assim:

 H
dA 1  ds 1   1  
.r .r v .r p
dt 2 dt 2 2.m 2.m
Daí, a velocidade areolar é diretamente proporcional à magnitude do momento
angular. Particularmente, no caso de movimento sujeito a força central, a
velocidade areolar é constante.
Isso se conforma ao que estabelece a segunda lei de Kepler (lei das velocidades):
“a reta que une um planeta ao Sol varre áreas iguais em intervalos de tempo
iguais.” Pode-se afirmar, então, que a segunda lei de Kepler constitui um caso
específico do princípio da conservação do momento angular.
De acordo com primeira lei de Kepler, é elíptica a órbita descrita por um planeta
em torno do Sol. As velocidades v P no periélio (menor distância ao Sol, rP ) e
v A no afélio (maior distância ao Sol, rA ) estão assim relacionadas:
151

152. m.rP .v P m.rA .v A
vP rA
vA rP
Ou seja: a velocidade é máxima no periélio e mínima no afélio.
O momento angular pode ser expresso, também, em termos da velocidade
angular ( = v.r). Assim:
H m.v.r m.r 2 . I.
Onde I ( m.r 2 ) é o momento de inércia da partícula.
Cotejando:
H I.
p m.v
O momento de inércia I da partícula em relação a O desempenha papel análogo ao da
massa m, assim como a velocidade angular é análoga à velocidade v.
De acordo com a segunda lei de Newton, a soma dos momentos, em relação a O,
das forças que atuam sobre o ponto material P é igual à variação, na unidade de

tempo, do momento angular ( H o ) desse ponto em relação a O. Assim, temos:

 dH o
Mo 0
dt
logo:

Ho cons tan te
  
Ho r (m.v )

onde r é o vetor posição de P.
Isso significa que:
- o momento angular do ponto material que se move sob uma força central
é constante, em módulo, direção e sentido
 
- o vetor posição r de P deve ser perpendicular ao vetor H o constante
152

153. 
Sendo o módulo de H o constante, temos:
r.m.v. sen ro .m.vo . sen o
Essa equação é aplicável ao movimento de qualquer ponto material sob ação de força
central.
Sabendo-se que v (componente transversal da velocidade) é dada por
d d
v r. e que H o m.r.v , temos: H o m.r 2 . .
dt dt
Então, no caso de força central, encontramos:
d
Ho m.r 2 . constante
dt
Calculemos o momento angular por unidade de massa (h):
Ho d
h r 2. constante
m dt
A relação obtida acima reforça o que fora apresentado anteriormente (na página
107).
Velocidade de escape
Com base na conservação da energia mecânica, pode-se mostrar que um corpo
de massa m “escapa” da atração gravitacional da Terra se a sua energia cinética
G.M T .m
inicial (no ponto de partida) for superior a (considerada nula a energia
RT
potencial num nível de referência muito afastado do centro da Terra). Isso porque
a sua energia total (cinética mais potencial) passa a ser maior do que zero num
ponto infinitamente distante.
Na ausência de efeitos associados à resistência do ar, a velocidade de escape de
um corpo, na superfície da Terra, é obtida de:
2.G.M T
ve
RT
153

154. Com os valores conhecidos de G, MT e RT, encontramos, para a velocidade de
escape o valor de 11,2km/s. Teoricamente, então, se um corpo for lançado para
cima com velocidade igual ou superior a essa, ele não retorna à superfície da
Terra. Estará, portanto, livre da atração gravitacional do planeta e atingirá
posições infinitamente distantes. Na prática, porém, a velocidade de lançamento
terá de ser bem maior do que 11,2km/s, já que não se podem desprezar os efeitos
da resistência do ar sobre um corpo viajando a tamanha velocidade.
Simetrias e leis de conservação
As leis de conservação da energia, do momento linear e do momento angular têm
validade geral, estendendo-se a toda a física, inclusive a sistemas microscópicos
descritos pela mecânica quântica. Com efeito, esses princípios gerais de
conservação estão relacionados com propriedades gerais dos sistemas físicos.
Diz-se que um sistema apresenta uma propriedade de simetria quando não se
altera quando nela efetuamos uma operação correspondente a essa simetria.
Nesse sentido, pode-se mostrar que a conservação da energia está associada à
uniformidade temporal, assim como a conservação do momento linear está
associada à homogeneidade espacial e a conservação do momento angular está
associada à isotropia espacial.
Seja um sistema constituído por N partículas ao qual está associada uma energia
potencial U (referente às forças externas e às forcas de interação entre as
partículas). Consideremos U como função dos vetores posição
   
(ri yi . j z i .k ) das partículas e do tempo.
xi .i
U U ( x1 , y1 , z1 ;...; x N , y N , z N ; t )
Se as partículas se deslocam entre os instantes t e t , ocorre variação de
energia potencial que assim se expressa:
U U U U U U U
U . x1 . y1 . z1 ... . xN . yN . zN . t
x1 y1 z1 xN yN zN t
  U
U Fi . ri . t
i t
Em não havendo forças externas dependentes do tempo atuando sobre o sistema,
temos:
U
0
t
Podemos escrever, então:
154

155.  ri   
dU U
lim lim Fi . Fi .vi
dt t 0 t t 0
i t i
Pela segunda lei de Newton, temos:
  
dvi  d 1  dEci
Fi .vi mi . .vi .mi .vi2
dt dt 2 dt
dU d dEc
Assim: Eci
dt dt i dt
dE M d
Isso equivale a ( Ec U ) 0 , ou seja, E M Ec U , que
dt dt
corresponde à lei da conservação da energia, obtida como conseqüência da
simetria por translação temporal do sistema.
Consideremos, agora, um sistema em que nada se altera se todo o sistema for
transladado. Neste caso, U pode se expresso por:
      
U U (r1 R,...,rN R) U (r1 ,...,rN ) R. Fi 0
i
  
dp i
F Fi 0
i i dt

  dP
Sendo P pi , temos: O , que corresponde à lei de conservação
i dt
do momento linear, obtida como conseqüência da simetria por translação espacial
do sistema.
Se, por outro lado, nada se altera no sistema, se o girarmos (infinitesimal) em
torno de um eixo qualquer, podemos expressar a variação de energia potencial
por:
          
U U (r1 ri ,...,rN rN ) U (r1 ,...,rN ) Fi . ri Fi .( ri ) 0
i i
155

156.    
Então, teremos: U . ri Fi . 0
i
 
onde i
i

 dH
Logo: 0, que corresponde à lei de conservação do momento
dt
angular, obtida como conseqüência da simetria por rotação espacial do sistema
(isotropia espacial).
No caso de um sistema isolado (no qual atuam somente forças internas) temos
uniformidade temporal, homogeneidade espacial e isotropia espacial. Portanto,
num sistema isolado são conservados a energia, o momento linear e o
momento angular.
156

157. Impulso e Quantidade de Movimento
O efeito que uma força produz sobre uma partícula depende não apenas das
qualidades dessa partícula (geometria, deformabilidade), mas também das
características próprias da força (intensidade, direção, sentido), do ponto de
aplicação e do tempo durante o qual ela atua. A simples identificação da força é,
portanto, insuficiente para a determinação de seus efeitos.
Em muitas situações, a força é aplicada num curto intervalo de tempo,
ocasionando os chamados movimentos impulsivos, que são de especial interesse
para o estudo da dinâmica.
Diversos movimentos impulsivos podem ser encontrados, por exemplo, nos
esportes: o de uma bola chutada por um jogador de futebol ou uma bola rebatida
por uma raquete de tênis. As colisões (choques) em geral envolvem processos
impulsivos.
Nesse caso, não apenas a força, mas também o seu comportamento temporal de
ação, devem ser considerados. Cabe, então, definir uma grandeza associe a força
e o tempo. Tal grandeza, de caráter vetorial, é o impulso e se expressa
matematicamente por
 
I F .dt
Variação da quantidade de movimento
Operando com a relação entre força e aceleração, expressa na segunda lei de
Newton, temos:   dv
F m.
dt
 
F .dt m.dv

O impulso da força F no intervalo de tempo entre t1 e t2 corresponde à integral:
 t2
  
I F .dt m.v2 m.v1
t1
Rearrumando os termos, obtemos:

t2
 
m.v1 F .dt m.v2
t1
A expressão acima traduz o princípio do impulso e quantidade de movimento e
pode ser empregado para a solução de problemas que envolvam força, massa,
157

158. velocidade e tempo, particularmente os casos de movimentos impulsivos ou
choques.

A quantidade de movimento final mv2 de um ponto material pode ser obtida

somando-se vetorialmente à quantidade de movimento inicial mv1 o impulso da

força F durante o intervalo que está sendo considerado.
Aplicações:
Problemas resolvidos:
1) Um corpo de massa 5kg assente
sobre uma superfície horizontal sem
atrito, inicialmente em repouso, recebe,

durante 10s, aplicação de uma força F ,
cujo módulo é 5N. Determine a
velocidade final desse corpo.
R.: O impulso equivale à variação da quantidade de movimento. Sendo o movimento
unidimensional, podemos operar algebricamente. Assim:
I F. t
I
5.10 50N.s
50 5.v 5.0 v 10m / s
2) Um corpo de massa m realiza movimento
circular uniforme com velocidade de módulo v
sobre um plano horizontal. Determine o
impulso produzido pela força resultante sobre
esse corpo no intervalo de tempo
correspondente ao seu deslocamento entre
os pontos A e B, na figura seguinte.
R.: Neste caso, não podemos relaxar o caráter vetorial das grandezas impulso e
quantidade de movimento. O impulso é obtido de:
  
I m.v B m.v A
Subtraindo os vetores, encontramos:
158

159. O módulo do impulso vale 2 .m.v .
O vetor impulso é orientado para o centro de curvatura da trajetória. Observe que a força
resultante é centrípeta.
Componentes do impulso

Denotando a força F em termos de suas componentes cartesianas, temos:
 t2
 t2
 t2

I Fx .dt .i Fy .dt . j Fz .dt .k
t1 t1 t1
Daí, podemos escrever escalarmente:
t2
m.v x 1
Fx .dt m.v x 2
t1
t2
m.v y 1
Fy .dt m.v y 2
t1
t2
m.v z 1
Fz .dt m.v z 2
t1
159

160. Sistema de partículas
Para um sistema de partículas que se move em relação a um sistema de
referência inercial, o princípio do impulso e quantidade de movimento se expressa
por:

t2
 
mi . vi 1
Fi .dt mi . vi 2
t1
 
dvi
onde: Fi mi .
dt

Fi corresponde à soma das forças externas atuantes sobre o sistema de
partículas.
Se nenhuma força externa atuar sobre os pontos materiais do sistema (ou se a
soma das forças externas for nula), temos, denotando por m a massa total do
sistema:
 
m.v1 m.v2
Ou seja: a quantidade de movimento total do sistema é conservada, o que é
compatível com o que foi apresentado no capítulo anterior.
Quantidade de movimento e energia cinética
A energia cinética de uma partícula pode ser expressa em termos de sua
quantidade de movimento. Consideremos uma partícula de massa m com
velocidade v. Sua energia cinética Ec pode ser expressa por:
1 (m.v) 2
Ec .m.v 2
2 2.m
p2
Ec
2.m
160

161. Aplicações:
Problemas resolvidos:

1) Considere uma bola de massa m movendo-se com velocidade v que, ao
atingir um plano vertical, segundo um ângulo , é rebatida com velocidade de
igual módulo, conforme figura seguinte. Determine a intensidade do impulso
recebido pela bola durante o contato com o plano.

R.: Seja v 1 a velocidade da bola logo após ser rebatida. Temos a seguinte relação:
  
I m.v1 m.v
Algebricamente: I m.v1 .sen m.v.sen (em módulo: v1 v)
Portanto: I 2.m.v.sen
2) Um projétil de massa 10kg se desloca no ar com velocidade de 25m/s, quanto
explode produzindo dois fragmentos A e B de massas, respectivamente, 3kg e
7kg, os quais, logo após a explosão, percorrem as direções indicadas na figura
seguinte. Determine a velocidade inicial de cada fragmento.
161

162. R.: Aplica-se, aqui, o princípio da conservação do momento linear (quantidade de
movimento), pois desprezam-se as forças externas sobre o sistema. Assim, a quantidade
de movimento antes da explosão (vetor de módulo 250kg.m/s, orientado para a direita)
equivale à soma (vetorial) da quantidade de movimento de cada uma das partes A e B.
Esquematicamente, temos:
Podemos estabelecer as seguintes relações algébricas:
250 3.v A . cos 45 o 7.v B . cos 30 o (componentes do momento linear na horizontal)
0 3.v A .sen 45 o 7.v B .sen30 o (componentes do momento linear na vertical)
Resolvendo o sistema de equações, encontramos:
v A 43,1m / s e vB 26 ,1m / s
3) Uma esfera de aço de massa m cai de
uma altura de h o numa canaleta curva
de raio R, como mostra a figura seguinte.
Ao sair da canaleta, a esfera atinge altura
máxima de h1 . Estime: i) o tempo em
que a esfera fica em contato com a
canaleta; ii) a força média que a canaleta
exerce sobre a esfera.

R.: Calculemos a velocidade v o com que a esfera ingressa na canaleta e a velocidade

v1 dessa esfera ao sair da canaleta na outra extremidade.
vo 2.g.ho
v1 2.g.h1
162

163. Se considerarmos constante a força de atrito ao longo da canaleta, temos que a força
tangencial é constante, resultando movimento uniformemente acelerado. Assim, podemos
estimar o tempo de permanência da esfera na canaleta, a partir do cálculo da aceleração
tangencial:
v12 vo2
at
2. .R
v1 vo
t
at
O impulso corresponde à variação da quantidade de movimento. Assim:
  
I m.v1 m.vo I m.v1 m.v o
A intensidade da força média pode ser estimada de:
I ( m.v1 m.v o )
F .a t
t v1 vo
4) Considere um foguete se movendo horizontalmente no vácuo, como mostra a
figura seguinte. Encontre a expressão da velocidade final do foguete, ou seja,
quando todo o seu combustível for consumido.
R.: Seja Mo a massa do foguete vazio (sem o combustível) e m a massa do combustível.
Assim, a massa total é M M o m .
Denotemos por v a velocidade do foguete (em relação à Terra) no instante inicial em que a
'
massa total seja M, e por v a velocidade de saída dos gases (em relação ao foguete)
nesse mesmo instante. Então, em relação à Terra a velocidade de saída dos gases vale
v' v , na direção contrária à de deslocamento do foguete.
Se num intervalo de tempo dt uma massa dm é ejetada do foguete, a massa do foguete
diminui também dm e, em conseqüência, a sua velocidade aumenta dv. Ocorre, então,
um aumento do momento do foguete igual a d(Mv) que deve ser equivalente à variação
que deve ocorrer com os gases ejetados. Portanto:
d (Mv) d (m.(v' v)) 0
Diferenciando, vem: d (Mv) v.dM M .dv
163

164. dM dm
v.dM M .dv dM .(v' v) 0
v'.dM M .dv
dM
dv v'.
M
Sendo nula a velocidade inicial v (quando o foguete ainda está com todo o seu
combustível), a velocidade final vf (quando o combustível se exauriu), apliquemos a
integração:
vf Mo
dM
dv v'.
v M
M
Mo m
Assim: vf v'.ln
Mo
Note-se que a velocidade dos gases ejetados está sendo considerada constante, durante
o processo de queima do combustível, o que é uma aproximação bastante razoável.
164

165. Colisões
O termo colisão se refere a uma situação genérica, da qual participam dois ou
mais corpos que entram em contacto. De modo particular, ocorrendo a colisão
entre dois corpos num cenário em que as forças de um sobre o outro são
relativamente intensas e atuam num intervalo de tempo muito curto, temos o que
denominamos choque.
Um choque é dito central quando os centros de massa dos dois corpos envolvidos
na colisão estão situados na normal de choque (normal comum às superfícies em
contacto durante o choque). Caso contrário, o choque é excêntrico.
Trataremos, aqui, somente dos choques centrais. Temos a destacar dois tipos de
choques centrais. Dizemos que o choque é direto quando as velocidades dos dois
pontos materiais possuem a direção da normal de choque; por outro lado, se os
pontos materiais se deslocam em retas não coincidentes com a normal de choque,
o choque assume caráter oblíquo.
choque direto choque oblíquo
A análise de choque direto é simples, pois somente uma dimensão do espaço é
considerada. Choques oblíquos podem envolver até três dimensões. A abordagem
seguinte alcança todos os choques centrais.
Considerando um sistema constituído por dois pontos materiais, em não havendo
impulso de força externa, a quantidade de movimento total é conservada.
Recordemos que o único elemento capaz de alterar a quantidade de movimento
total de um sistema é o impulso oferecido pela ação de forças externas ao
sistema. Em todo caso, a variação da quantidade de movimento será igual ao
impulso.
165

166.   
Qinicial I Q final
Seja um sistema constituído de n corpos de massa m1, m2, ..., mn, cada um
  
dotada de velocidade, respectivamente, v1 , v 2 , ..., vn . Na ausência de forças
externas ao sistema, podemos estabelecer:
  
m1 .v1 m2 .v 2 ... mn v n cons tan te
Devemos estar sempre atentos ao caráter vetorial das expressões precedentes.
Na situação mais simples de colisão, envolvendo dois corpos, a relação vetorial do
teorema do impulso e quantidade de movimento pode ser retratada esquematicamente
como na figura seguinte. Nela, dois corpos colidentes A e B, num plano; eles se aproximam
um do outro com velocidades, respectivamente, (vA)1 e (vB)1.
Cada um desses corpos sofre uma variação na sua quantidade de movimento equivalente
ao impulso recebido durante o choque. Na direção y, a quantidade de movimento se
conserva tanto para A quanto para B, pois o impulso tem direção x, ou seja, não há
componente de impulso na direção y. Ao longo da linha de impacto, a quantidade de
movimento total do sistema é conservada. Assim:
166

167. Ao analisarmos o comportamento de um dos corpos envolvidos na colisão, antes,
durante e após o choque, identificamos um período de deformação e um período
de restituição. A cada um desses períodos podemos associar um impulso,
responsável por alteração em sua quantidade de movimento. A razão dos módulos
desses impulsos (de restituição e de deformação) é denominada coeficiente de
restituição (e), que pode assumir valor no intervalo de 0 a 1, dependendo
principalmente da natureza dos materiais envolvidos, mas também sendo função
da velocidade de choque e da forma e tamanho dos corpos.
FR .dt
e
FD .dt
onde FR é a força de restituição e FD, a força de deformação.
Efetivamente, o coeficiente de restituição, grandeza adimensional que deve ser
conhecida em problemas de colisão, expressa a razão entre a velocidade relativa
dos corpos em choque, antes e após o fenômeno.
Assim, a partir do conhecimento de e fica fácil determinar a velocidade que cada
um dos corpos apresenta depois da ocorrência do choque, bastando, para isso, a
resolução do sistema de equações seguinte:
  ' ' '
m A .v A m B .v B m A .v A m B .v B
' '
vB vA e.( vB vA )
167

168. Na expressão acima, (v B
'
v A ) corresponde à velocidade de afastamento dos
'
corpos colidentes (após o choque) e (v B v A ) corresponde à velocidade de
aproximação (antes do choque).
A primeira das duas equações precedentes pode, no caso mais geral, se
desdobrar em três equações de grandezas escalares, cada uma delas referente a
um dos três eixos perpendiculares que formam o sistema de referência cartesiana.
Assim:
' ' '
m A .v Ax m B .v Bx m A .v Ax m B .v Bx
' ' '
mA .v Ay mB .vBy mA .v Ay mB .vBy
' ' '
m A .v Az m B .v Bz m A .v Az m B .v Bz
Nos extremos do intervalo de e reconhecemos dois casos de interesse particular,
quais sejam, o do choque perfeitamente plástico e o do choque perfeitamente
elástico. No primeiro, os dois corpos prosseguem solidários, inexistindo velocidade
relativa entre eles; e assume valor nulo. As equações precedentes adquirem, em
conjunto, o aspecto seguinte, onde v’ denota a velocidade comum dos corpos.
  
m A .v A m B .v B (m A m B ).v '
No segundo caso especial, e tem valor unitário, indicando a preservação da
velocidade relativa. Os corpos prosseguem separados após o choque com a
mesma velocidade relativa com que se aproximaram. Temos, então, que a energia
total dos dois pontos materiais é conservada, assim como a quantidade de
movimento total. Assim, chegamos a:
1 2 1 2 1 1
.m A .v A .mB .v B .m A .(v A ) 2
'
.mB .(v B ) 2
'
2 2 2 2
Ou seja, a energia cinética total dos pontos materiais é conservada. Isso não
acontece no caso geral de choques, mas somente quando e vale 1. Noutra
situação, a energia cinética “perdida” é parcialmente transformada em calor e em
ondas elásticas no interior dos dois corpos.
168

169. A análise de choques centrais oblíquos se desenvolve sem embaraços se
atentarmos para os mesmos princípios norteadores que comentamos
anteriormente. Sendo as forças de interação recíproca entre os corpos na direção
da normal de choque, consideração essencial do choque central, somente nessa
direção haverá mudança nas componentes da quantidade de movimento de cada
um dos corpos envolvidos; porém, mesmo nessa direção (normal de choque), a
conservação se verifica na componente da quantidade de movimento total dos
pontos materiais. Na direção que lhe é perpendicular, a componente da
quantidade de movimento de cada ponto material é mantida antes e após a
colisão. Vale salientar: a igualdade entre impulso e variação da quantidade de
movimento deve ser assumida vetorialmente, já que estamos lidando com
grandezas dotadas de intensidade, direção e sentido.
Aplicações:
Problemas resolvidos:
1) Considere uma bola de aço caindo de uma altura h1 sobre uma placa de aço.
Após o impacto, ela retorna alcançando uma nova altura h2. Determine: i) o
coeficiente de restituição; ii) a altura que a bola alcançará após a segunda queda.
R.: Velocidade da bola imediatamente antes do choque (velocidade de aproximação):
v 2.g.h1
Velocidade da bola imediatamente após o choque (velocidade de afastamento):
v' 2.g.h2
O coeficiente de restituição relaciona essas duas velocidades. Assim:
v' h2 h2
e
v h1 h1
Após a segunda queda, a bola atinge uma altura h3 tal que:
h3 h3
e
h2 h2
h2
Então: h3 e 2 .h2 .h2
h1
2
h2
h3
h1
169

170. 2) Dois blocos, de massas mA e mB, deslizam sobre uma superfície horizontal sem
atrito. A figura seguinte indica as velocidades imediatamente antes do choque.
Sendo e o coeficiente de restituição, determine: i) a velocidade de cada bloco após
o choque; ii) a energia dissipada durante o choque.
R.: Trata-se de um choque direto.
Considerando o sistema formado pelos dois blocos, sem forças externas impulsivas, temos
a conservação da quantidade de movimento do conjunto, embora cada bloco,
individualmente, sofra alteração na sua quantidade de movimento. Assim:
  ' '
m A .v A m B .v B m A .v A m B .v B
onde v A e v B denotam as velocidades na direção x de A e B, respectivamente, logo
' '
após a colisão.
A relação entre as velocidades relativas, imediatamente após e imediatamente antes do
choque, se expressa pelo coeficiente de restituição e.
  ' '
e.( v A vB ) vA vB
Em termos algébricos, podemos compor o seguinte sistema de equações:
' '
m A .v A m B .v B m B .v B m A .v A
' '
v B v A e.(v A v B )
A resolução do sistema acima permite conhecer as velocidades de A e B após o choque.
A energia mecânica dissipada durante o choque é obtida de:
1 2 1 2 1 ' 2 1 ' 2
E .m A .v A .m B .v B .m A . v A .m B . v B
2 2 2 2
1 2 ' 2 2 ' 2
E . mA . vA vA mB . v B vB
2
Note-se que quando o coeficiente de restituição é unitário, a variação E é nula.
3) Considere que a bola de bilhar mostrada na figura seguinte se mova com

velocidade v e atinja a lateral da mesa primeiramente no ponto A e em seguida no
ponto B. O coeficiente de restituição entre a bola e a lateral da mesa vale e.
170

171. Desprezando as dimensões da bola, encontre a expressão de sua velocidade após
a segunda colisão.
R.: Temos, na primeira colisão:
v'.cos v. cos 45
v' 2
v 2. cos
v'.sen
e tg e
v.sen 45
Na segunda colisão:
v' '. cos v ' . cos(90 )
v' '. cos v ' .sen
v' ' sen
v' cos
v' '.sen
e tg .tg e
v ' . cos
tg 1
Portanto: v '' v.e
171

172. 4) Duas esferas lisas iguais se chocam. As velocidades imediatamente antes do
choque estão indicadas na figura seguinte. O coeficiente de restituição vale 0,8.
Determine a velocidade de cada bola logo após a colisão.
R.: Trata-se de um choque oblíquo.
Sejam os eixos x e y, respectivamente, paralelo e
perpendicular à normal de choque.
As velocidades vA e vB decompostas segundo esses eixos se expressam por:
v Ax v A . cos 30 o 7,8m / s v Bx v B . cos 120 o 6,0m / s
o o
v Ay v A .sen30 4,5m / s v By v B .sen120 10,4m / s
Na direção perpendicular à normal de choque, não atua qualquer força impulsiva. Assim,
não haverá alteração na componente y da quantidade de movimento de nenhuma das
bolas. Portanto:
v Ay 4,5m / s e v By 10 ,4m / s
Na direção paralela à normal de choque, muda a quantidade de movimento de cada uma
das bolas, no entanto, a quantidade total de movimento do conjunto é conservada. Então:
' '
m A .v Ax m B .v Bx m A .v Ax m B .v Bx
onde v Ax e v Bx denotam as velocidades na direção x de A e B, respectivamente, logo
' '
após a colisão.
A relação entre as velocidade relativas, expressa pelo coeficiente de restituição, permite
escrevermos:
' '
v Bx v Ax e.( v Ax v Ax )
Substituindo os valores, encontramos o seguinte sistema de equações:
' '
v Ax v Bx 1,8
' '
v Bx v Ax 12,42
172

173. Daí resulta:
' '
v Ax 5,31m / s e v Bx 7,11m / s
' '
Recompondo os vetores velocidade v A e v B , temos:
velocidade de A velocidade de B
173

174. 174

175. Listas de Exercícios
1ª. Lista
1.1 Sendo x expresso em metros, t em segundos e v em m/s, determine as
unidades das constantes em cada uma das funções seguintes:
i) x c1 .t c 2
ii) v
c2 .t
c1 .e
iii) v 2 4.c1 .x
iv) x cos(c1 .t )
c1 .c 2
v) x c1 .t c1 .c 2 c3 c 4 . cos( )
c5
1.2 Apresente, com dois algarismos significativos, o valor da grandeza que se
expressa por
1/ 2
.v
F .t
sendo =1,0.10 J ; v=7,2km/h ; F=1,0N e t = 2,5s.
-3
1.3 Apresente, com três algarismos significativos, o valor da grandeza que se
expressa por
b2
a
c d
sendo a=1,44.106cm/s ; b=2,00.108cm/s ; c=4,70.103km/s e
d=6,51.105m/s.
1.4 Apresente, com dois algarismos significativos, em unidade SI, o valor da
grandeza que se expressa por
.a
b2
sendo a=1,80g/cm² e b=1,2003x10-2s/m².
175

176. 1.5 Ao sofrer uma transição, em que a sua energia muda de Ei para Ef, um elétron
emite um fóton, cuja freqüência pode ser calculada por
Ei Ef
h
onde h=4,14.10-15 eV.s (h: constante de Planck) e Ei e Ef os níveis energéticos
inicial e final.
Sendo, por exemplo: Ei=1,4.104 eV e Ef=0
Expresse o valor da freqüência, com o número correto de algarismos significativos.
1.6 Suponha, a priori, que a expressão do período (T) de um pêndulo simples, de
pequena oscilação, seja um monômio das grandezas físicas massa (m),
comprimento do fio (l) e aceleração da gravidade (g). Encontre os expoentes das
grandezas intervenientes e mostre que, de fato, o período não depende da massa.
1.7 Apresente a equação dimensional da potência de uma força, definida como a
razão entre o trabalho e o tempo, em termos das dimensões de força (F),
velocidade (v) e tempo (t).
176

177. 2ª. Lista
2.1 Uma partícula se move em trajetória retilínea, sendo a sua posição definida por
s (t 3 2.t 2 ) m, onde t é o tempo expresso em segundos. Determine a
aceleração dessa partícula no instante 2s.
2.2 Uma bola de tênis é solta de uma altura de 4,00m. Ela quica no chão e sobe
até a altura de 3,00m. Sendo o tempo de contato com o chão de 10,0ms,
determine a aceleração média durante esse contato.
2.3 O gráfico seguinte retrata o movimento de uma partícula em linha reta. No
instante inicial, sua posição é -12m. Determine os instantes em que a partícula
passa pela origem.
2.4 Um veículo trafega numa estrada retilínea, variando a sua aceleração
conforme a figura seguinte. Sendo a velocidade no instante inicial 5m/s, determine
para o instante 12s: i) a velocidade; ii) a distância percorrida.
177

178. 2.5 A uma altura y acima da superfície da Terra, a aceleração da gravidade se
9,81
expressa por g 2
, sendo g em m/s² e y em metros. Um
y
1
6,37.10 6
projétil é disparado verticalmente para cima com velocidade inicial de 3000m/s.
Determine a altura alcançada.
2.6 Um trem e um automóvel deslocam-se paralelamente, num mesmo sentido em
trecho retilíneo. Os seus movimentos são uniformes e a velocidade do automóvel é
o dobro da do trem. Desprezando-se o comprimento do automóvel e sabendo-se
que o comprimento do trem é de 200m, determine o espaço percorrido pelo
automóvel desde o instante em que alcança o trem até o instante em que o
ultrapassa.
2.7 Um elevador está subindo com velocidade constante de 3,6km/h. Uma
lâmpada se desprende do teto e atinge o piso do elevador 0,8s depois. Determine
a altura do elevador, desprezando a resistência do ar.
2.8 Um balão sobe verticalmente com velocidade constante de 600m/min. Em
dado instante, solta-se do balão uma bomba que explode ao atingir o solo. Um
observador no interior do balão ouve a explosão 12s após a partida da bomba.
Determine a altura do balão no instante em que a bomba foi abandonada.
2.9 Considere a roda mostrada na figura seguinte, em que o ponto central desloca-

se horizontalmente, com velocidade constante v . Identifique a trajetória descrita
pelos pontos A, B e C.
178

179. 2.10 Um barco atravessa um rio de largura l. A velocidade da água do rio é nula
nas margens e aumenta uniformemente em direção ao centro, onde é máxima de
valor v R . A velocidade própria do barco é constante igual a v B e dirigida sempre
perpendicularmente às margens do rio. Determine: i) o tempo que o barco leva
para atravessar o rio; ii) a equação cartesiana da trajetória do barco na travessia.
2.11 Considere o sistema de cordas e
polias mostrado na figura seguinte.
Num dado instante, a extremidade da
corda é puxada para baixo com
velocidade de 1m/s desacelerando à
taxa de 0,5m/s². Determine, para esse
instante, a velocidade e a aceleração
do bloco A.
2.12 Um veículo com velocidade constante de 3m/s puxa um bloco, como mostra a
figura seguinte. Determine a velocidade do bloco em função do ângulo .
179

180. 3ª. Lista
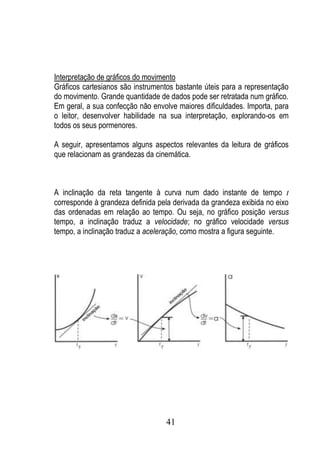
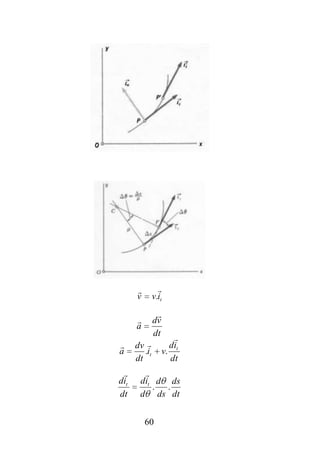
3.1 Considere a partícula P da figura seguinte movendo-se numa trajetória definida
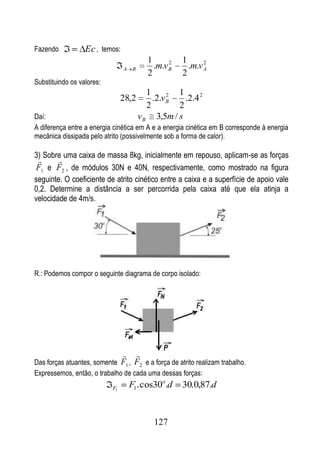
pelo seguinte vetor-posição:
  
r [ A. cos(a.t )].i [ B.sen (a.t )]. j .
Mostre que a aceleração é voltada para a origem e proporcional à distância da
partícula à origem.
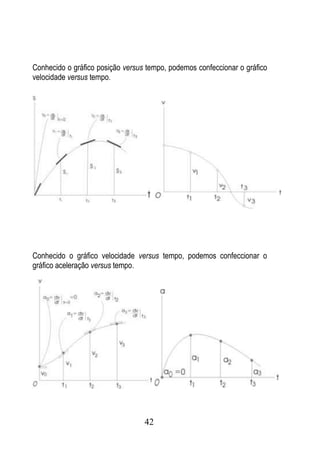
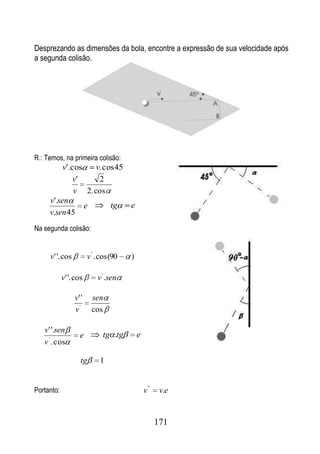
3.2 Uma partícula se movimenta com velocidade de módulo constante v o numa
trajetória descrita pela equação y a.sen(b.x) . Determine as componentes da
velocidade segundo as direções x e y , num instante qualquer.
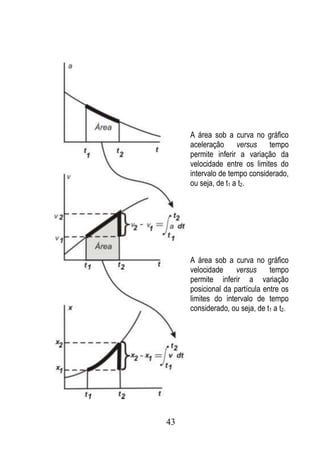
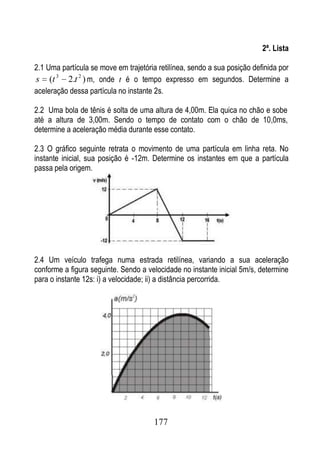
3.3 Um tanque de pressão apresenta orifício em A, por onde a água escoa com
velocidade horizontal vo, conforme ilustra a figura seguinte. Determine a faixa de
valores de vo para que a água atravesse a abertura BC.
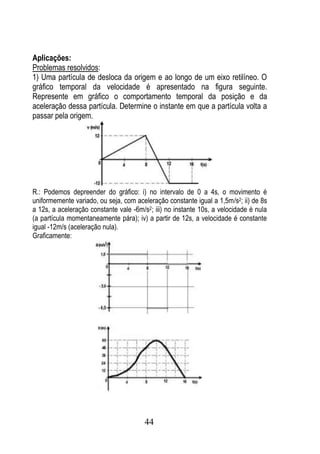
3.4 Mostre que o raio de curvatura da trajetória de um projétil é mínimo no ponto
mais alto dessa trajetória.
180

181. 3.5 Um bombeiro, segurando um bocal em A, esguicha água com velocidade
inicial de 10m/s segundo um ângulo de 60o com a horizontal. Determine: i) o ponto
do telhado alcançado por jato de água; ii) a faixa de valores de velocidade inicial
para que o telhado seja atingido pela água.
3.6 A bola da figura seguinte é abandonada verticalmente sobre o ponto A do
plano inclinado e atinge, após o rebote, o ponto B. Determine: i) a velocidade do
rebote em A; ii) o tempo que a bola leva para ir de A a B.
3.7 Uma flecha é atirada com velocidade inicial 60m/s, num ângulo de 15º com a
horizontal, do plano inclinado mostrado na figura seguinte. Determine: i) a
distância horizontal percorrida pela flecha antes de novamente atingir o plano
inclinado de lançamento; ii) o raio de curvatura da trajetória imediatamente após o
lançamento; iii) o raio de curvatura da trajetória no instante em que a flecha atinge
a sua máxima elevação.
181

182. 3.8 Uma bola é lançada por um jogador com velocidade de 15m/s, num local
coberto, conforme ilustra a figura seguinte. Determine a máxima altura yB possível
de ser alcançada pela bola.
3.9 Uma bola é arremessada contra uma parede vertical situada a 5m de distância
do ponto de lançamento, o qual se dá com velocidade de 15m/s segundo um
ângulo de 45o com a horizontal e a 2m do piso, conforme ilustra a figura seguinte.
Ao atingir a parede, a componente vertical da velocidade não se altera e a
componente horizontal da velocidade é invertida. Determine o ponto, no solo, que
a bola irá tocar.
3.10 Uma mangueira contra incêndio lança água com velocidade inicial 24m/s, que
atinge o ponto B do edifício, conforme ilustra a figura seguinte. Determine: i) a
182

183. altura máxima alcançada pela água; ii) o ângulo correspondente a essa máxima
altura.
3.11 Uma pequena esfera escorrega, sem atrito, sobre uma superfície,
descrevendo ¼ de circunferência de raio R. No instante em que a partícula
abandona a superfície, no ponto A, uma outra pequena esfera é solta nesse
mesmo nível, num ponto da vertical distante d de A. Mostre que as duas partículas
se encontrarão, qualquer que seja o valor de d.
3.12 Uma bola é lançada do ponto mais alto de uma rampa, conforme ilustra a
figura seguinte. Considerando que essa bola deve alcançar a rampa da direita,
determine: i) o máximo valor de h; ii) a velocidade inicial mínima.
183

184. 3.13 Considere um trilho, em plano vertical, formato de parábola e vértice tangente
ao eixo x na origem. Do ponto de coordenadas (-2,0; +3,0), abandona-se um
corpo de dimensões desprezíveis. Assume-se também desprezível o atrito entre o
corpo e o trilho. Determine: i) as acelerações tangencial e normal do corpo no
instante em que a altura acima do vértice do trilho é de 1,5m; ii) o ponto em que a
aceleração é nula; iii) o ponto em que a aceleração é máxima; iv) o ponto em que
a velocidade é máxima; v) o ponto mais alto que o corpo atinge após passar pelo
ponto mais baixo de sua trajetória.
3.14 Considere um plano inclinado de ângulo com a horizontal, continuado por
um arco de parábola expressa por x 2 120 . y (x horizontal e y vertical, como
origem no ponto inferior do plano inclinado). Uma partícula é abandonada de uma
altura 10m nesse plano e desliza sem atrito. Determine o ponto mais alto que a
partícula atingirá sobre a parábola.
184

185. 4ª. Lista
4.1 Para a situação de equilíbrio mostrada na figura seguinte, determine i) a
massa m desconhecida; ii) a tensão em cada corda.
 
4.2 Considere um corpo de massa 2kg submetido às forças F1 e F2 expressas,
em N, por
  
F1 2.i 2. j
  
F 2 3.i j
Determine a aceleração adquirida por esse corpo.
4.3 Um corpo de massa 2kg desloca-se em trajetória retilínea. O comportamento
temporal da velocidade é retratado na figura seguinte. Represente graficamente a
força resultante versus o tempo.
4.4 Considere a situação mostrada na figura seguinte, em que um homem de
massa 70kg está numa cabine de massa 25kg. Determine a força que o homem
deve aplicar à corda para que o sistema (homem e cabine) suba com aceleração
constante de 1,5m/s2.
185

186. 4.5 A escada AB, uniforme e homogênea,
com comprimento l e peso p E , está
apoiada numa parede vertical, como
mostra a figura seguinte. O coeficiente de
atrito estático entre a escada e o solo vale
. Um homem de peso pH consegue subir
5/6 da extensão da escada sem que haja
escorregamento. Determine: i) a
intensidade da força exercida sobre a
escada pela parede; ii) o coeficiente de
atrito estático entre a escada e a parede.
4.6 No sistema apresentado na figura seguinte, cada uma das roldanas apresenta
massa desprezível podendo girar sem atrito em torno do respectivo eixo. Os fios
são inextensíveis, perfeitamente flexíveis e de massas desprezíveis. As massas
m1, m2 e m3 dos blocos presos aos extremos dos fios são tais que
m1 m2 m3
m2 2.m3
Avalie a condição de equilíbrio da massa m1 ao ser retirada a prancha sobre a qual
estão apoiados dos três blocos.
186

187. 4.7 Para a situação apresentada no problema anterior, determine a aceleração que
cada bloco adquire, quando retirada a prancha que os apóia.
4.8 Os dois planos inclinados da figura seguinte podem ser fixados em qualquer
posição, girando-os em torno da aresta horizontal comum. Os blocos A e B, de
mesma massa, estão ligados entre si por um fio inextensível de massa desprezível
e podem deslizar sem atrito sobre os planos inclinados. Determine a posição dos
planos para a qual os blocos se movem com máxima aceleração.
4.9 Determine a inclinação do telhado de uma casa para que a água da chuva
permaneça sobre ele o menor tempo possível.
4.10 Considere os blocos A e B, de mesma massa, nas situações mostradas nas
figuras seguintes. Os coeficientes de atrito entre todas as superfícies são iguais

entre si, de valor . A força F1 imprime uma velocidade constante ao sistema
187

188.   
constituído pelos dois blocos. Determine a relação entre F2 e F1 , e entre F3 e

F1 , de modo que os blocos B se movam com velocidades constantes.
4.11 Os blocos A e B, mostrados na figura seguinte, não estão fixados um ao
outro. Suas massas são, respectivamente, 15kg e 75kg. Entre os blocos o
coeficiente de atrito estático vale 0,35; entre o bloco B e o piso não há atrito.
Determine a mínima força F capaz de manter o bloco A em contato com B, sem
deslizar.
4.12 Pretende-se que os blocos A e B, da figura seguinte, movimentem-se juntos.
O bloco A tem massa 4,0kg e o B, 5,0kg. Desconhece-se o valor do coeficiente
de atrito entre eles; no entanto, constata-se que, mantido o bloco B fixo, é
necessária uma força horizontal mínima de 10N aplicada sobre o bloco A para que
este inicie movimento. O plano sobre o qual estão os dois blocos não oferece
qualquer atrito. Determine: i) a força horizontal máxima a ser aplicada sobre o
bloco B; ii) a aceleração do conjunto.
4.13 Um corpo de massa m sobre uma mesa polida está preso a um outro corpo
de massa M através de um fio que passa pelo furo no centro da mesa, como
mostrado na figura seguinte. O corpo de massa M está em repouso. Caracterize o
comportamento do corpo de massa m.
188

189. 4.14 Considere os blocos A e B, de massas 10kg e 15kg, respectivamente,
colocados juntos num plano inclinado e, em seguida, liberados, como mostra a
figura seguinte. Entre o bloco A e o plano inclinado, o coeficiente de atrito vale
0,20; entre o bloco B e o plano inclinado, o coeficiente de atrito vale 0,10.
Determine: i) a aceleração de cada bloco; ii) a força que o bloco A exerce sobre o
bloco B.
4.15 Dois corpos, A e B, de mesma massa 30kg, estão sobre um plano inclinado
de 15o. O coeficiente de atrito entre A e B vale 0,10; o coeficiente de atrito entre
A e o plano inclinado vale 0,20. Os corpos são liberados do repouso. Determine: i)
a aceleração de cada placa; ii) a inclinação mínima para que o corpo A inicie
movimento; iii) o que aconteceria se A e B fossem soldados.
189

190. 4.16 Um veículo está subindo uma rampa cuja inclinação é de 3%, a uma
velocidade constante de 60km/h. O motorista mantém a marcha durante todo o
trajeto. Determine a aceleração do veículo quando este começar a trafegar num
trecho plano horizontal da estrada.
4.17 A máquina de Atwood ilustrada na figura
seguinte é submetida a uma força ascendente

F . A massa da polia é m P . Determine: i) a
aceleração da cada massa; ii) a tensão no fio.
190

191. 5ª. Lista
5.1 Uma caixa está sobre um vagão de trem aberto que se move à velocidade v. O
coeficiente de atrito estático entre a caixa e o piso do vagão vale e. O trem deve
ser desacelerado à aceleração constante e a caixa não deve deslizar sobre ele.
Determine o percurso mínimo de frenagem.
5.2 Numa ferrovia, pretende-se que os trilhos interno e externo, distantes d um do
outro, sejam tais que as forças suportadas pelas rodas do trem tenham a mesma
intensidade, numa curva de raio , quando o veículo trafega a uma velocidade v.
Determine a diferença de nível entre os trilhos.
5.3 Um motociclista gira na parede lateral de um cilindro circular de eixo vertical e
raio , descrevendo uma circunferência horizontal. O coeficiente de atrito entre os
pneus e a parede do cilindro vale . Determine a menor velocidade tangencial
possível. Compare esse valor com o que seria obtido caso o cilindro tivesse eixo
horizontal.
5.4 Considere o sistema mostrado na figura seguinte. Os dois blocos apresentam
igual massa, de 30kg. Despreze qualquer atrito. Determine: i) a aceleração de
cada bloco; ii) a tensão no cabo.
5.5 Sobre uma superfície plana e horizontal, um veículo se desloca, conduzindo
um plano inclinado, conforme mostra a figura seguinte. Sobre o plano inclinado é
colocado um bloco cujo coeficiente de atrito com o plano vale . Determine a
máxima aceleração do veículo, de modo que o bloco não se mova em relação ao
plano inclinado.
191

192. 5.6 Um carro deve fazer, sem derrapar, uma curva horizontal de raio , com uma
velocidade v. A estrada é superelevada para velocidade v’ menor do que v.
Determine o coeficiente de atrito mínimo entre a estrada e os pneus do veículo.
5.7 Um ciclista pedala numa estrada horizontal, devendo fazer uma curva de raio
com uma velocidade v. Determine a inclinação que deve ser dada ao corpo, em
relação à vertical, de modo que não haja um acidente de queda.
5.8 Uma força F é aplicada ao bloco A (de peso PA) da figura seguinte. Não há
atrito entre as superfícies em contato. Determine a aceleração do bloco B (de peso
PB).
5.9 Os blocos A e B mostrados na figura seguinte apresentam massas iguais.
Entre eles, o coeficiente de atrito estático é e. Entre o bloco B e a superfície
horizontal de apoio não há atrito. O bloco A não desliza sobre o bloco B.
Determine o máximo valor da força F aplicada ao bloco B.
192

193. 5.10 Considere o sistema de corda e polias mostrado na figura seguinte. O bloco A
tem massa 5kg. Num dado instante, o colar move-se para a esquerda com
velocidade de 5m/s estando desacelerado de 2m/s2. Determine, para esse
instante, a tração no cabo conectado ao colar.
5.11 Uma esteira transportadora lança pacotes de massa 1kg com velocidade de
1m/s numa rampa circular lisa de raio 0,5m, como ilustra a figura seguinte.
Determine o ponto em que cada pacote deixa de ter contato com a superfície.
193

194. 5.12 Um pequeno bloco de gelo é colocado no topo de uma cúpula hemisférica
(raio R) de vidro. O gelo começa a deslizar e, num certo ponto, perde o contato
com a superfície. Finalmente, o bloco atinge um ponto no plano horizontal onde se
encontra a cúpula hemisférica. Estime: i) a velocidade com que o gelo chega ao
ponto do plano horizontal; ii) as coordenadas do ponto em que o gelo perde
contato com a cúpula.
194

195. 6ª. Lista
6.1 Considere a situação mostrada na figura seguinte, em que o corpo de massa
m1 é preso a um fio de comprimento L1, cuja outra extremidade é fixa em ponto de
um plano horizontal onde não há atrito. Um outro corpo de massa m2 está preso
ao primeiro por um fio de comprimento L2. Os dois descrevem movimento circular,
de período de revolução T. Determine a tensão em cada fio.
6.2 Considere o disco mostrado na figura seguinte, preso por u’a mola ao centro
de u’a mesa (superfície plana horizontal). O comprimento indeformado da mola é
xo. A tensão na mola é diretamente proporcional à sua deformação. O disco gira
com freqüência f. Encontre as expressões do raio R e da tensão na mola T.
6.3 Na situação mostrada na figura seguinte, uma bola de massa 1,2kg está presa
a um eixo girante por duas cordas de massa desprezível, cada uma de 1,7m. As
cordas estão estiradas. A tensão na corda superior vale 35N. Determine: i) a
tensão na corda inferior; ii) a força resultante sobre a bola; iii) a velocidade da
bola.
195

196. 6.4 Considere ainda o arranjo mostrado na figura anterior, porém com o eixo
girante na horizontal. Determine: i) a mínima velocidade da bola para que as
cordas estejam sempre distendidas; ii) a tensão em cada corda.
6.5 Os arames AC e BC estão presos a uma esfera de massa 5kg e esta gira
numa circunferência horizontal com velocidade constante, de tal modo que a
tensão assume o mesmo valor nos dois arames. Determine: i) a velocidade da
esfera; ii) a tensão em cada arame.
6.6 As molas M1 e M2, de constantes elásticas k1 e k2, respectivamente,
apresentam o mesmo comprimento indeformado lo. Despreze a massa de cada
mola. As molas são associadas de duas maneiras, conforme ilustra a figura
seguinte. Determine a constante elástica equivalente em cada uma das
associações.
196

197. 6.7 Dois blocos de mesma massa m são
interligados por fio e suspensos, também por
fios, ao teto, em duas situações, conforme
ilustra a figura seguinte. Na situação da
esquerda, os fios estão estirados (sem
deformação); na situação da direita, os dois
blocos são aproximados um do outro e soltos
em seguidos. Os dois fios são idênticos e
apresentam limite de ruptura de 1,5 vezes o
valor do peso de cada bloco. Identifique o
primeiro fio a romper-se. Comente.
197

198. 7ª. Lista
7.1 Considere um satélite em órbita circular em torno da Terra. Mostre que a sua
energia total equivale à metade da respectiva energia potencial.
7.2 Um barco a motor atravessa um rio de largura l e velocidade de corrente v R . O
ponto de chegada à margem oposta está situado a uma distância x abaixo do
ponto de partida. Durante a travessia, a velocidade própria do barco é mantida
constante igual a v B , sempre dirigida perpendicularmente à corrente do rio. O

motor imprime constantemente uma força F . Determine a potência desenvolvida
durante a travessia por esse motor.
7.3 Considere dois blocos A e B interligados, como mostra a figura seguinte. Entre
B e a superfície horizontal há atrito (coeficiente de atrito cinético c). Encontre a
expressão da velocidade desses blocos (liberados a partir do repouso), após
percorrerem uma distância l.
7.4 Duas partículas de mesma massa partem de uma mesma posição A,
simultaneamente, com a mesma velocidade inicial, pretendendo alcançar a
mesma posição final B. Uma delas percorre a trajetória a, passando sobre uma
colina de altura h; a outra segue a trajetória b, que atravessa um vale de
profundidade h. A figura seguinte (corte vertical) esclarece. As partículas estão
sujeitas apenas à ação da força gravitacional e da força normal da superfície.
Identifique, justificadamente, qual das partículas chega primeiro ao fim de sua
trajetória.
198

199. 7.5 Um pequeno bloco é liberado em A com velocidade nula e move-se ao longo
da guia, sem atrito, em direção ao ponto B, onde deixa a guia com velocidade
horizontal. Sendo h igual a 2,40m e b igual a 0,9m , determine: i) a velocidade
(módulo, direção e sentido) do bloco ao atingir o solo em C; ii) a distância
correspondente c.
7.6 Um bloco de peso 2,5N é solto em A e desliza sem atrito ao longo da
superfície ilustrada. Determine a força exercida pela superfície sobre o bloco
quando este passa pelos pontos B e C.
199

200. 7.7 Num plano vertical é disposto um trilho, conforme ilustra a figura seguinte. Uma
partícula é abandonada no ponto A e desliza sem atrito sobre o trilho. Determine: i)
o ponto no qual o corpo perde contato com o trilho; ii) a trajetória descrita pelo
corpo em queda livre.
7.8 Na situação da figura seguinte, um saco com areia é puxado suavemente do
topo de uma parede em A e oscila num plano vertical na extremidade de uma
corda de 4m, capaz de suportar uma tensão máxima igual ao dobro do peso do
saco. Determine: i) a altura em que a corda se rompe; ii) a distância da parede
lateral ao ponto em que o saco atingirá o piso.
7.9 A corda mostrada na figura tem comprimento L igual a 120cm e a distância d
até o pino fixo P é 75cm. Quando a bola é liberada em repouso na posição
indicada na figura, a trajetória é descrita pela linha tracejada. Determine: i) a
velocidade da bola ao passar pelo ponto mais baixo da trajetória; ii) a velocidade
da bola ao chegar ao ponto mais alto da trajetória, após tocar o pino.
200

201. 7.10 Um pequeno bloco de massa m desliza sem atrito na pista mostrada na
figura. Sendo o bloco liberado do repouso no ponto P, determine a força resultante
que age sobre ele no ponto Q.
7.11 Com base nos elementos fornecidos no problema precedente, determine de
que altura (em relação ao ponto mais baixo da pista) o bloco deve ser liberado
para esteja na iminência de perder contato com a pista no ponto mais alto do
semicírculo.
7.12 Um colar de 100N desliza sem atrito em uma barra vertical, como mostrado
na figura. A mola presa ao colar possui, quando não deformada, um comprimento
de 0,1m e constante de 600N/m. Se o colar é solto do repouso na posição 1,
determine sua velocidade após ter-se deslocado, para baixo, 0,15m (ponto 2).
201

202. 7.13 Um veículo de massa m é acelerado a partir do repouso, numa estrada
horizontal, a potência constante P. Determine: i) a velocidade do veículo em
função do tempo; ii) a função horária da posição.
7.14 Uma esteira transportadora lança pacotes de massa 1kg com velocidade de
1m/s numa rampa circular lisa de raio 0,5m, como ilustra a figura seguinte.
Determine o ponto em que cada pacote deixa de ter contato com a superfície. 13
7.15 Uma partícula de massa 5kg está submetida a uma força horizontal cuja
intensidade varia conforme o gráfico seguinte. Determine a velocidade dessa
partícula após percorrer 2m.
13 Este problema foi apresentado em lista anterior, atinente a aplicação das leis de Newton da
dinâmica. Sua reapresentação aqui significa que ele deve ser resolvido por um caminho alternativo,
isto é, a partir do princípio do trabalho e energia.
202

203. 7.16 Um bloco de 10kg é solto no ponto A e desliza ao longo de uma superfície
circular lisa, quando, então, encontra uma superfície áspera com 1m de extensão
(entre os pontos B e C). Adiante, esse bloco atinge uma mola de constante
elástica 50N/m, conforme ilustra a figura seguinte. Determine a deformação da
mola até o bloco parar.
7.17 No sistema mostrado na figura seguinte, um cursor de massa m e extensão
Lc repousa sobre uma barra lisa, na posição central. A esse cursor são fixadas
duas molas, de constantes elásticas k e k’, cada uma delas presa a uma das
extremidades da barra. O comprimento indeformado cada mola é L. O cursor é,
então, deslocado x para a direita e liberado do repouso. Determine a sua
velocidade no instante em que ele retorna à sua posição original.
203

204. 7.18 Considere na situação da figura seguinte um bloco de massa 3kg
pressionado contra a mola comprimida de 1m, no ponto A. O plano inclinado
percorrido não oferece atrito. Determine a distância d até o bloco atingir o solo.
7.19 Uma bolinha de massa 400g e
dimensões desprezíveis deve ser lançada
num trilho vertical circular. Um pistão
mantém a mola comprimida 10cm, na
situação mostrada na figura seguinte.
Determine: i) a distância s que o pistão deve
ser puxado (para trás) e em seguida liberado,
de modo que a bolinha percorra todo o trilho,
alcançando a plataforma B; ii) a velocidade
da bolinha em B.
204

205. 8ª. Lista
8.1 Um projétil é lançado, a partir do solo, segundo um ângulo de 45º. Ao
atingir o ponto mais alto da trajetória, a 20m de altura, esse projétil explode,
fragmentando-se em duas partes, de mesma massa. Um dos fragmentos cai
verticalmente com velocidade de 30m/s. Determine: i) a altura máxima
atingida pelo outro fragmento; ii) a distância que esse fragmento percorre
horizontalmente ao retornar ao solo.
8.2 Uma bola cai verticalmente e ao chocar-se com uma placa rígida é
rebatida na horizontal, como ilustra a figura seguinte. O coeficiente de
restituição do choque vale e. Determine: i) o valor do ângulo ; ii) o módulo
da velocidade de rebatimento.
8.3 Duas bolas iguais A e B se chocam, sendo que a linha de colisão forma
um ângulo de 30o com a vertical, como ilustra a figura seguinte. O
coeficiente de restituição do choque vale 0,8. Determine a velocidade de
cada uma das bolas logo após o choque.
205

206. 8.4 O bloco A, de massa 1kg, é liberado, desliza sem atrito e se choca com
a bola B, de massa 2kg, que está inicialmente parada, como mostra a figura
seguinte. O coeficiente de restituição vale 0,8. Determine: i) a velocidade de
cada uma das bolas imediatamente após o choque; ii) a tensão máxima no
fio; iii) a máxima altura alcançada pela bola B.
8.5 Uma bola abandonada no ponto A atinge o ponto C, após chocar-se
com uma placa rígida, como mostra a figura seguinte. O coeficiente de
restituição vale 0,7. Determine a distância horizontal entre os pontos B e C.
8.6 Mostre que num choque perfeitamente elástico a velocidade relativa das
duas partículas é a mesma antes e depois da colisão.

8.7 Uma bolinha é lançada horizontalmente com velocidade v , como
mostrado na figura seguinte. O coeficiente de restituição entre a bola e o
piso vale e. Determine: i) a velocidade da bola no instante imediatamente
206

207. após chocar-se com o piso; ii) a altura máxima h2 alcançada pela bola após
o primeiro rebatimento.
8.8 Considere um bloco de massa M solto de uma altura h sobre um prato
de massa m, numa balança de mola, como mostra a figura seguinte. A
constante elástica da mola sob o prato vale k e o choque é suposto
perfeitamente plástico. Determine a máxima deflexão do prato.
207

208. Bibliografia recomendada
BEER, F. P.; JOHNSTON Jr., E. R. Mecânica vetorial para engenheiros –
Dinâmica, vol. 2, 3ª. Edição, Editora McGraw-Hill do Brasil, São Paulo,
1980.
BRENNAN, R. Gigantes da física – uma história da física moderna através
de oito biografias, trad. Maria Luíza Borges, Jorge Zahar Editor, Rio de
Janeiro, 1998.
CARMONA, H. A. Energia e movimento, Edições Demócrito Rocha – UECE,
Fortaleza, 2002.
FERENCE Jr., MICHAEL; LEMON, HARVEY B.; STEPHENSON,
REGINALD J. Curso de Física – Mecânica, trad. José Goldemberg,
Editora Edgard Blücher Ltda / Universidade de São Paulo, São Paulo,
1968.
FEYNMAN, R. Física em seis lições, trad. Ivo Korytowski, 3ª. Edição,
Ediouro, Rio de Janeiro, 1999.
HALLIDAY, D.; RESNICK, R.; WALKER, R. Fundamentos de Física, vol. 1,
4a. edição, Livros Técnicos e Científicos Editora S.A., Rio de Janeiro,
1996.
HIBBELER, R. C. Mecânica – Dinâmica, 8ª. Edição, Livros Técnicos e
Científicos Editora S.A., Rio de Janeiro, 1999.
MAIA, L. P. M. Problemas de Mecânica, Editora Latino-Americana, Rio de
Janeiro, 1960.
NUSSENZVEIG, H. M. Curso de Física Básica - Mecânica, vol. 1, 3ª.
Edição, Editora Edgard Blücher Ltda., São Paulo, 1996.
TIPLER, P. A. Física – Mecânica, Oscilações e Ondas, Termodinâmica, vol.
1, 4ª. Edição, Livros Técnicos e Científicos Editora S.A., Rio de Janeiro,
2000.
PERELMAN, Y. Física Recreativa, vols. I e II, Rubiños, Madrid, 1994.
POSKITT, K. Mortos de fama – Isaac Newton e sua maçã, trad. Eduardo
Brandão, Cia. das Letras, São Paulo, 2001.
208