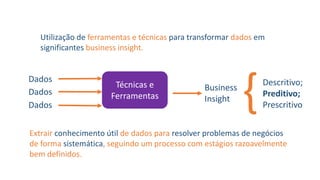
1) O documento apresenta uma introdução ao curso de Business Analytics, definindo o objetivo de capacitar os alunos a entender, modelar e resolver problemas de negócios usando técnicas estatísticas no R. 2) Business Analytics envolve transformar dados em insights valiosos para os negócios através de ferramentas e técnicas estatísticas. Inclui domínios como marketing, clientes, processos e cadeia de suprimentos. 3) A análise de dados requer entendimento de conceitos como ciência de dados, estr

1. Business Analytics
Professor Luiz Alves
luizalvesadm@gmail.com

2. Aula 01 Introdução à Business
Analytics

3. INTRODUÇÃO
Por favor, apresente-se:
- nome;
- empresa / universidade;
- cargo;
- expectativa deste curso.

4. OBJETIVO: Capacitar o aluno a entender, modelar e resolver
problemas de Business Analytics, acessando bases de dados
em planilhas e bancos de dados, através do uso de ferramentas
estatísticas R.

5. REFERÊNCIAS
FAWCETT, Tom; PROVOST, Foster. Data Science para negócios: O que você
precisa saber sobre mineração de dados e pensamento analítico de
dados. Alta Books Editora, 2018.
HAIR, Joseph F. et al. Análise multivariada de dados. Bookman Editora,
2009.
MALHOTRA, Naresh K. Pesquisa de Marketing-: Uma Orientação
Aplicada. Bookman Editora, 2001.
WICKHAM, Hadley; GROLEMUND, Garrett. R for data science: import,
tidy, transform, visualize, and model data. " O'Reilly Media, Inc.", 2016.
OLIVEIRA, Paulo Felipe; GUERRA, Saulo; MCDONNELL, Robert. Ciência de
dados com R: Introdução. Brasília: Editora IBPAD, 2018

6. O que é Business Analytics?

7. Dados
Técnicas e
Ferramentas
Business
Insight
Dados
Dados
Descritivo;
Preditivo;
Prescritivo
Utilização de ferramentas e técnicas para transformar dados em
significantes business insight.
{
Extrair conhecimento útil de dados para resolver problemas de negócios
de forma sistemática, seguindo um processo com estágios razoavelmente
bem definidos.

8. OS DOMÍNIOS DO
BUSINESS ANALYTICS
Análise de marketing
Análise do cliente
Análise de serviço
Análise de recursos humanos
Análise de talentos
Análise de processo
Análise da cadeia de suprimentos
Análise de risco
Análise financeira

9. BI X BA
BUSINESS
INTELLIGENCE
BUSINESS
ANALYTICS

10. TERMINOLOGIA DA ANÁLISE DE DADOS

11. Ciência de dados envolve princípios, processos e técnicas para compreensão
dos fenômenos através da análise (automatizada) dos dados.
Estratégia de dados refere-se à estratégia para criar e capturar valor dos
dados (existentes ou novos).
- Requer pensamento analítico de dados: poder avaliar se e como os dados podem
melhorar o desempenho.
A tomada de decisão baseada em dados refere-se à prática de fundamentar
decisões sobre dados em vez de pura intuição.

12. Big Data é o termo em Tecnologia da Informação (TI) que trata sobre
grandes conjuntos de dados.
-5 V’s – volume, variedade, velocidade, veracidade e valor.
Mineração de dados é a extração de conhecimento dos dados, via
tecnologias que incorporam os princípios da ciência de dados.
- A implementação prática da ciência de dados
- A mineração de dados é mais restrita que a ciência de dados, mas os
termos geralmente são usados intercambiáveis.
Engenharia de dados refere-se às tecnologias usadas para armazenar
e processar Big Data.
- Em apoio, não em vez de, ciência de dados.

13. QUESTÕES - DISCUTA COM SEU VIZINHO
Quais empresas você acredita que utilizam Business
Analytics (BA)?
Como e com qual objetivo é utilizado?
Você acredita que o BA está trazendo valor para essas
empresas?

14. Os benefícios do Business Analytics
• Brynjolfsson, Hitt & Kim (2011) demostraram que, estatisticamente,
quanto mais uma empresa é orientada por dados, mais produtiva é a
empresa.
• A tomada de decisão baseada em dados está associada a um
aumento de 4% a 6% na produtividade. A tomada de decisão
baseada em dados também está correlacionado com maior retorno
sobre ativos, retorno sobre patrimônio, utilização de ativos e valor
de mercado, e o relacionamento parece ser causal.
Brynjolfsson, Erik and Hitt, Lorin M. and Kim, Heekyung Hellen, Strength in Numbers: How Does Data-Driven
Decisionmaking Affect Firm Performance? (April 22, 2011). Available at
SSRN: https://ssrn.com/abstract=1819486 or http://dx.doi.org/10.2139/ssrn.1819486

15. DADOS CAPACIDADE DE EXTRAIR
CONHECIMENTO ÚTIL DOS
DADOS
ATIVOS ESTRATÉGICOS

16. The Cross Industry
Standard Process
for Data Mining
(CRISP-DM)

17. FUNCIONALIDADES
DO BUSINESS
ANALYTICS
1. Classificação e Scoring
2. Estimativa de valor (regressão)
3. Análise de similaridade
4. Agrupamento (Clustering)
5. Agrupamento de co-
ocorrência(associação)
6. Criação de perfil
7. Previsão de Link
8. Redução de dados
9. Modelagem causal

18. Abandono do carrinho de compras de uma loja on-line, e.g.
Magazine Luiza
como podemos usar os dados para prever e / ou impedir o
abandono do carrinho de compras
abandono (por exemplo, começar, mas não terminar) até certo
ponto.
- Nota: prever não implica necessariamente prevenção!
- Prevenir requer 'ação': a capacidade de afetar o preditor antes
para o resultado (por exemplo, sexo x design da página x canal
de aquisição)
• Para cada uma dessas tarefas diferentes de mineração de
dados, pense em um aplicação que pode ajudar esse problema
(não necessariamente resolvê-lo completamente)

19. CLASSIFICAÇÃO E SCORING
Classificação significa prever para cada indivíduo, ou seja qual de um
conjunto de classes (mutuamente exclusivas) esse indivíduo pertence.
Scoring (ou estimativa de probabilidade de classe) fornece uma
pontuação para cada indivíduo que representa a probabilidade desse
indivíduo pertencer a cada uma das classes.
- Por exemplo: esse cliente abandonará (sim / não) vs. qual é o
probabilidade de esse cliente (não) abandonar?
Outras aplicações?

20. Estima um valor numérico para cada cliente
- tenta estimar ou prever, para cada indivíduo, o valor numérico
de alguma variável para esse indivíduo.
Aplicação ao abandono de carrinho de compras?
Outras aplicações?
ESTIMATIVA DE VALOR

21. Identificar indivíduos semelhantes com base em dados conhecidos
sobre eles.
- Também conhecida como segmentação.
- As medidas de similaridade estão subjacentes a certas soluções
para outras tarefas de mineração de dados, como classificação,
regressão e clustering.
Aplicação ao abandono de carrinho de compras?
Outras aplicações?
ANÁLISE DE SIMILARIDADE

22. Agrupar indivíduos com base na semelhança (sem um objetivo
específica em mente)
- Forma de redução de dados, geralmente útil para obter um sentido
para os dados "
Aplicação ao abandono de carrinho de compras?
Outras aplicações?
AGRUPAMENTO (CLUSTERING)

23. Baseado em transações, em vez de individual: Quais são os itens nas
transações associadas com mais frequência?
Também conhecida como análise de cesta de mercado no marketing,
ou regra de associação.
Aplicação ao abandono de carrinho de compras?
Outras aplicações?
ANÁLISE DE ASSOCIAÇÃO

24. Caracterizar o comportamento de indivíduos, grupos ou populações.
- Qual é o comportamento "típico"?
- Frequentemente útil para identificar comportamentos atípicos (por
exemplo, fraude).
Aplicação ao abandono de carrinho de compras?
Outras aplicações?
PERFIL

25. Previsão de conexões entre itens de dados: um link (forte) deve estar
lá, mas não está lá.
- Por exemplo: identificando possíveis novas conexões no Linkedin ou
recomendação de filmes no Netflix.
Aplicação ao abandono de carrinho de compras?
Outras aplicações?
PREVISÃO DE LINK

26. Reduzir um enorme conjunto de dados para algo mais gerenciável, sem
perder muitas informações importantes.
- Clustering como exemplo, mas existem outros métodos também.
- As forças se concentram nos aspectos mais importantes.
Aplicação ao abandono do carrinho de compras?
Outras aplicações?
REDUÇÃO DE DADOS

27. Quais eventos / ações realmente influenciam outros eventos / pessoas?
- “Correlação não é causalidade”.
- Para previsão, a correlação costuma ser suficiente ("céu é azul"); para intervenções / ações, é
necessária causalidade.
Extremamente útil para os negócios, mas geralmente requer uma substancial investimento
na obtenção dos dados certos.
- Os dados que existem frequentemente não são suficientes para a causalidade.
- Experimentos de campo!
Requer pensamento analítico de dados!
Aplicação ao abandono de carrinho de compras?
Outras aplicações?
MODELAGEM CAUSAL

28. Você tem um resultado
desejado?
Se sim, então
supervisionado, se não,
então não supervisionado
Não supervisionado:
- Associação
- Clustering
- Criação de perfil
Supervisionado:
- Classificação
- Similaridade
- Estimativa de valor
- Previsão de link
- Modelagem causal

29. FERRAMENTAS COMPUTACIONAIS

30. FERRAMENTAS DE GERENCIAMENTO DE DADOS

31. FERRAMENTAS DE VISUALIZAÇÃO DE DADOS

32. FERRAMENTAS DE ANÁLISE DE DADOS

33. O QUE É O R?
R é uma linguagem de programação estatística que vem
passando por diversas evoluções e se tornando cada vez
mais uma linguagem de amplos objetivos. Podemos
entender o R também como um conjunto de pacotes e
ferramentas estatísticas, munido de funções que facilitam
sua utilização, desde a criação de simples rotinas até análises
de dados complexas, com visualizações bem acabadas.

34. Instalando o R
https://www.r-project.org/
https://rstudio.com/
Linguagem R
Interface – R Studio

35. Objetos do R (O que são?)
Existem muitos tipos de objetos no R que só passamos a conhecê-los bem com
o passar do tempo. Por enquanto vamos aprender os tipos básicos de objetos.
a) vetores: uma sequência de valores numéricos ou de caracteres (letras,
palavras).
b) matrizes: coleção de vetores em linhas e colunas, todos os vetores dever ser
do mesmo tipo (numérico ou de caracteres).
c) dataframe: o mesmo que uma matriz, mas aceita vetores de tipos diferentes
(numérico e caracteres). Geralmente nós guardamos nossos dados em objetos
do tipo dataframe, pois sempre temos variáveis numéricas e variáveis
categóricas (por exemplo, largura do rio e nome do rio, respectivamente).

36. FUNÇÕES

37. PACOTES
Pacotes são conjuntos extras de funções que podem ser
instalados além do R base. Existem pacotes para auxiliar as
diversas linhas de estudo que você possa imaginar:
estatística, econometria, ciências sociais, medicina,
biologia, gráficos, machine learning etc.
install.packages (“tidyverse”)

38. Aula 02 Entendendo e
Preparando os dados

39. O que são dados?

40. ▪
Dados são um conjunto de valores formados a
partir do cruzamento de casos com variáveis
Dado é o resultado de investigação,
cálculo ou pesquisa
Variável é toda
característica que
pode
assumir diversos
valores conforme
pessoa,
objeto ou coisa.
Unidade elementar é
qualquer pessoa,
objeto ou coisa que faça
parte de uma
população.

41. Variável
Quantitativa
Qualitativa
não pode ser
operada
algebricamente
pode ser operada
algebricamente
Nominal
Ordinal
Continua
Discreta

42. QUESTÕES - DISCUTA COM SEU VIZINHO
Responda a lista de variáveis (entregue em sala) com (N)
nominal; (O) Ordinal; (C) continua; (D) discreta.

43. ESCALA DE MEDIÇÃO

44. Medição significa atribuir números
ou outros símbolos às características
dos objetos que estão sendo
medidos, de acordo com as regras
pré-determinadas.
.
São medidas as características do
objeto, não o objeto diretamente.
Números geralmente são atribuídos
por dois motivos:
- Permitir a análise estatística dos
dados gerados.
- Ajudar a comunicar as informações
sobre os resultados.

45. O escalonameto é uma parte da medição
As escalas utilizada para
medir as características dos
objetos ao longo de um
continuum

46. ESCALA DE MEDIÇÃO
Escala Característica Exemplos
Estatística
Admissíveis
Nominal Números que identificam e classificam
objetos
Sexo, região, gosta/ não
gosta, número de
identificação do
funcionário
Porcentagens, moda
Ordinal Números que indicam as posições
relativas dos objetos, mas não a
importância das diferenças entre eles.
Classes Sociais,
preferências, cargo
Percentil, mediana
Intervalo Diferenças entre objetos que podem
ser comparadas; o ponto zero e
arbitrário.
Atitudes, opiniões Intervalo, media,
desvio-padrão
Razão Ponto zero e fixo; os valores das
proporções das escalas podem ser
computados
Preço, número de
clientes, volume de
vendas, renda
Média geométrica,
media harmônica

47. MEDIDAS

48. Medidas de posição central
.
Mediana
Moda
Média
Medidas de dispersão
.
Amplitude
Desvio-médio
Variância
Desvio-padrão
Medidas de ordenamento
.
Mediana
Quartis
Decis
Centis ou Percentis

49. PREPARANDOS OS DADOS
INCLINAÇÃO
Simétrica Assimétrica Moderada Assimétrica
0,15 1,0

50. CURTOSE
C=0 (mesocúrtica) C>0 (leptocúrtica) C<0 (platicúrtica)

51. O que houve com minha
análise?

52. Preparando os Dados
Análise Descritiva dos Dados
Análise das Observações Atípicas (Outlier)
Análise dos dados faltantes (Missing Value)
Testes de Suposições

53. summary.data.frame()
Histograma
hist()
• Assimetria
library(e1071)
skewness(x, type=2)
Análise Descritiva no R
Curtose
library(e1071)
kurtosis(x,type=2)
Relação entre as variáveis
Variável vs Variável
plot()
plot(density())
Matriz de Dispersão
pairs()

54. • library(ggplot2)
• Relação entre as variáveis
ggplot(data = dabase) +
geom_point(mapping = aes(x = v1, y = v2,
color = class))
geom_point(mapping = aes(x = v1, y = v2))
• Análise de variável
geom_bar(mapping = aes(x = cut))
Análise Descritiva no R

55. São observações com uma combinação única de características
identificáveis como sendo notavelmente diferente das outras
observações.
Não podem ser categoricamente caracterizadas como benéficas
ou problemáticas.
É importante averiguar seu tipo de influência.
Observações Atípicas (Outlier)

56. 1º Erro de procedimento
(erro na entrada de dados ou uma falha na codificação)
2º Resultado de um evento extraordinário detectável
3º Observações extraordinárias inexplicáveis
4º Observações com valores possíveis, mas com combinação
extraordinária entre as variáveis.
Classes de observações atípicas (outliers)

57. 1º Erro de procedimento
(erro na entrada de dados ou uma falha na codificação)
2º Resultado de um evento extraordinário detectável
3º Observações extraordinária inexplicável
4º Observações com valores possíveis, mas com combinação
extraordinária entre as variáveis.
Classes de observações atípicas (outliers)

59. Por meio do Boxplot
boxplot()
boxplot.stats ()
Identificação das observações atípicas
(outliers) no R
Por meio da biblioteca
library(outliers)
#superior
outliers ()
#inferior
outliers(x,
oppositive=TRUE)

60. Devem ser mantidas, a menos que exista prova demonstrável de que estão
verdadeiramente fora do normal e que não são representativas de quaisquer
observações na população.
Se as observações atípicas são eliminadas, o analista de dados corre o risco de
melhorar a análise multivariada, mas limita sua generalidade.
Eliminação dos outliers

61. Técnicas a serem implementadas:
Trimming ou Winsorinzing (Hawkings, 1980)
Eliminação dos outliers
10, 15,16,17,22
Trimming
Winsorinzing
15,16,17
15, 15,16,17,17

62. A preocupação primária do analista de dados é determinar as
razões inerentes aos dados perdidos.
O analista deve compreender os processos que conduzem os
dados perdidos a fim de selecionar o curso de ação apropriado.
Dados faltantes (missing value)

63. Incluir somente observações com dados completos.
Eliminar as variáveis problemáticas.
Utilizar métodos de atribuição.
Ações corretivas para os dados faltantes (missing
value)

64. O método de atribuição é um processo de estimação de valores
perdidos com base em valores válidos de outras variáveis e/ou
observações na amostra.
Principais métodos de atribuição:
Substituição por um caso
Substituição por média
Atribuição por regressão.
Utilizar métodos de atribuição

65. library(e1070)
impute(x, what = c("median", "mean")
library(imputeTS)
na.interpolation(mydata) # Interpolação linear
na.mean(mydata, option = "mean") # Média atribuição
na.mean(mydata, option = "median") # Mediana atribuição
Utilizar métodos de atribuição no R

66. SUPOSIÇÕES DA ANÁLISE MULTIVARIADA

67. Normalidade
Os dados devem ter uma distribuição que seja correspondente a
uma distribuição normal.
Esta é a suposição mais comum na análise multivariada.
Kolmogorov-Smirnov, Jarque-Bera e Shapiro-Wilks são exemplos de
teste que tentam identificar se uma determinada variável possui
distribuição normal.

68. Normalidade no R
#Shapiro-Wilks
shapiro.test()
#Kolmogorov-Smirnov
ks.test(x, “pnorm”, mean(x), sd(x))
p-value>0,05 - conjunto de dados foi extraído de uma população
com distribuição normal (não rejeita a H nula)

69. Homocedasticidade
Homocedasticidade significa igualdade de variância entre as
variáveis, referindo-se à suposição de que as variáveis dependentes
exibem níveis iguais de variância ao longo do domínio das variáveis
independente.
ANALISAREMOS NA PRÓXIMA AULA.

71. Linearidade
A linearidade pode ser usada para expressar o conceito de que um
modelo possui as propriedades de aditividade e homogeneidade,
sendo que os modelos lineares prevêm valores que recaem em uma
linha reta.
ANALISAREMOS NA PRÓXIMA AULA.

72. Aula 03 Modelo Preditivo
(Regressão linear
Múltipla)

73. Data Mining Processo:
construindo e usando
um modelo preditivo

74. Modelagem preditiva é um método para estimar um desconhecido valor de
interesse, que o chamado target.
Definir
target
Coletar
dados
Construir
o modelo
Predizer o
resultado

75. 1 variável dependente e 1
independente
Y = a + 𝒃𝟏𝒙𝟏+ 𝐮
Regressão Linear Simples
1 variável dependente e 2 ou mais
independentes
Y = a + 𝒃𝟏𝒙𝟏 + 𝒃𝟐𝒙𝟐+ 𝒃𝟑𝒙𝟑 + 𝐮
Regressão Linear Múltipla
Regressão Linear é uma
modelagem preditiva que
permite a análise do
relacionamento entre uma
variável dependente e uma ou
mais variáveis explicativas.

78. ▪ Seleção de variáveis;
▪ Análise dos pressupostos;
▪ Estimação dos parâmetros do modelo;
▪ Teste da significância do modelo;
Sequência de rotinas

79. ▪ Podemos selecionar a melhor variável independente com base nos
coeficientes de correlação (r)
Regressão Simples

80. Correlação
Mede a força do relacionamento, ou
grau de associação, entre 2 variáveis.
▪ – 1 = correlação linear negativa
perfeita
▪ 0 = nenhuma correlação linear
▪ + 1 = correlação linear positiva
perfeita
R² = % de variação em y explicada por x.

81. Em um estudo realizado durante 15 meses em uma academia de
ginástica, o propósito foi identificar quais fatores afetavam seus gastos.
Foram identificados 3 fatores potenciais:
• Consumo de Kilowatts – variável x1;
• Horas de MOD – variável x2;
• Número de alunos – variável x3;
Exemplo – Regressão Linear Simples

82. #Correlação dos Dados
cor() # por Default Coeficiente de Pearson
# Regressão Simples
lm(x~y)
#Encontra os coeficientes
summary(lm(x~Y))
Regressão Simples no R

83. Coeficiente de determinação (R²) indica a proporção que a variação da
variável dependente y é explicada pela variável independente x ou pelo
conjunto de variáveis
Resultados da Regressão

84. Teste F: Significância da Regressão. Tem por finalidade testar o efeito
conjunto das variáveis explicativas sobre a variável dependente;
Significa verificar se, pelo menos, uma das variáveis independentes do
modelo exerce alguma influência sobre a variável dependente.
Resultados da Regressão

85. Utilizando o mesmo Banco de Dados
Recorreremos à matriz de correlação para escolher a próxima variável a
entrar na regressão.
A variável x1 tem a segunda maior correlação com a variável
dependente (0,762);
Exemplo – Regressão Linear Multipla

86. #Regressão Múltipla
lm(x~y+z...+n)
#Encontra os coeficientes
summary(lm(x~Y))
Regressão Múltipla no R

87. Na regressão múltipla trabalha-se com o R² Ajustado
Reflete o número de variáveis explicativas e o tamanho da amostra;
R² Ajustado = R² corrigido pelos graus de liberdade da regressão
Resultados da Regressão

88. Correlação de uma variável
independente e a dependente
quando já existem outras variáveis
independentes na regressão.
▪ Representa o efeito preditivo
incremental de uma variável
independente não explicado
pelas variáveis independentes
que já estão na regressão;
▪ Utilidade: identificar as
variáveis independentes com o
maior poder preditivo
incremental;
Correlação Parcial
Y
x2 x1

89. # Calcular a Correlação Parcial
library(ppcor)
pcor ()
# Acréscimo esperado no valor do R²
Aumento do R² = (1-R²) x (r_parcial)²
quantidade inexplicada correlação parcial
Correlação Parcial no R

90. • Pressupostos na
• análise de regressão
Quando se tratar de regressão múltipla,
a entrada das variáveis na regressão
deve respeitar o valor preditivo adicional
revelado pelo conceito de correlação
parcial.

91. Pressupostos na análise de regressão

92. A aplicação apropriada de um
procedimento estatístico depende do
cumprimento de um conjunto de
pressupostos que, no caso da análise de
regressão
Conjunto de pressupostos
▪ Linearidade dos coeficientes e das
variáveis
▪ Normalidade dos resíduos
▪ Homocedasticidade dos resíduos
▪ Ausência de autocorrelação dos
resíduos
▪ Multicolinearidade das variáveis
independentes

93. Lineariedade
Representa o grau em que a variação na variável
dependente é associada com a variável
independente.
Diagnóstico - o diagrama de dispersão dá uma boa
ideia sobre a linearidade das variáveis x e y.

94. Lineariedade no R
#diagrama de dispersão com a variável dependente
(x)
plot(x,y)

95. Normalidade
Os resíduos devem apresentar distribuição
normal.
Diagnóstico gráficos ou testes estatísticos
– Kolmogorov–Smirnov , Shapiro-Wilks.

96. Normalidade
Os resíduos devem apresentar distribuição
normal.
Diagnóstico gráficos ou testes estatísticos
– Kolmogorov–Smirnov , Shapiro-Wilks.

97. Ausência de autocorrelação
Os resíduos são independentes.
Diagnóstico: gráficos ou testes estatísticos – Durbin–
Watson.
Autocorrelação: fenômeno em que os erros parecem
estar correlacionados com os demais.

98. Ausência de autocorrelação no R
Library(lmtest)
#teste de Durbin-Watson
dwtest(função da regressão linear)
# Analise do teste
p-value>0,05
“regra de bolso” DW próximo de 2 atendem ao
pressuposto.

99. Homocedasticidade
Os resíduos devem se distribuir de forma aleatória em torno da reta. A
variância dos resíduos deve ser constante para todos os valores de x.
Presença de variâncias não homogêneas – heteroscedasticidade –
violação dos pressupostos de regressão;
Diagnóstico - gráficos ou testes estatísticos: Pesaran–Pesaran, Quandt–
Goldfeld, Glejser, Park.

100. Homocedasticidade no R
# Observando a Homoscedasticidade graficamente
plot(model$residuals~y)
Modelo
plot(model)

101. Homocedasticidade - Pesaran–Pesaran no R
O teste consiste em detectar a presença de
heterocedasticidade com base nos resultados da
regressão em que a variável dependente representa
os valores dos quadrados dos resíduos e a
independente é constituída pelo quadrado dos
valores previstos da variável dependente.

102. Homocedasticidade - Pesaran–Pesaran no R
#Pesaran–Pesaran
#criar dois objetos com os resultados do modelo
Zre_2 – quadrado dos resíduos padronizados
Zpr_2 – quadrado dos valores estimados
# Cria a regressão dos dois modelos
lm(Zre_2~Zpr_2)
# verificar teste F
Sig>0,05

103. Multicolinearidade
O problema da multicolinearidade é uma questão de
grau e não de natureza – sempre existirá correlação.
Consequências:
Os coeficientes da regressão apresentam
▪ grandes erros–padrão;
▪ Imprecisão dos parâmetros estimados;
▪ Prejuízo na interpretação dos resultados.

104. Multicolinearidade
Diagnóstico de multicolinearidade:
• R2 alto e coeficientes de regressão não
significativos – pvalue > 0,05;
• Testes – Farrar e Glauber, FIV (fator de
Inflação da Variância).

105. Multicolinearidade
A situação ideal para todo pesquisador seria ter
diversas variáveis independentes altamente
correlacionadas com a variável dependente, mas com
pouca correlação entre elas próprias.

106. Multicolinearidade no R
library(faraway)
vif(model)
#Draper e Smith (1998) recomendam que valores de
VIF maiores do que 10 podem causar sérios
problemas na estimação dos coeficientes de
regressão.

107. Aula 04 Modelo Preditivo –
Classificação e Scoring
(Regressão Logística)

108. Data Mining Processo:
construindo e usando
um modelo preditivo

109. The Cross Industry
Standard Process
for Data Mining
(CRISP-DM)

110. Regressão Logística
Buscar predizer ou explicar a ocorrência de determinados fenômenos em
função de valores conhecido de outras variáveis.
Sendo a variável dependente de natureza binária
Exemplo: positivo ou negativo, aceitar ou rejeitar,
morrer ou sobreviver

111. Regressão Logística
Variável
Dependente
1 – 100% de chance de ocorrer o evento
0 – 0% de chance de ocorrer o evento
=

112. Regressão Logística
𝑓 𝑥 =
1
1+𝑒−(𝑏0+𝑏1𝑥1+𝑏2𝑥2+⋯+𝑏2𝑥2
“A curva mais importante
do mundo” (Pedro
Domingos, The Master
Algortim,2015)

113. Regressão Logística
𝑓 𝑥 =
1
1+𝑒−(𝑏0+𝑏1𝑥1+𝑏2𝑥2+⋯+𝑏2𝑥2
Exemplo: probabilidade de passar no vestibular
Target: qual é a probabilidade de um estudante X passar no
vestibular de medicina.
P 𝑝𝑎𝑠𝑠𝑎𝑟 =
1
1+𝑒−(−7+0,2.ℎ𝑜𝑟𝑎𝑠 𝑒𝑠𝑡𝑢𝑑𝑎𝑑𝑎𝑠)
Variável independente: Horas de Estudo no Mês.
horas
passar

114. Regressão Logística
𝑓 𝑥 =
1
1+𝑒−(𝑏0+𝑏1𝑥1+𝑏2𝑥2+⋯+𝑏2𝑥2
Exemplo: probabilidade de um cliente não renovar um contrato
Target: qual é a probabilidade de um cliente X não renovar o
contrato no próximo três mês.
P 𝑝𝑎𝑠𝑠𝑎𝑟 =
1
1+𝑒−(20+0,1.𝑟𝑒𝑛𝑑𝑎)
Variável independente: renda.
horas
Não
renovar

115. Classificação com Regressão Logística

116. Classificação
Não compradores de
seguro de vida
1 – 100% de comprar
0 – 0% de comprar
= 0,6 – 60% de comprar
Comprar
seguro de vida
(resposta = sim
/não
compradores de
seguro de vida
Identificar o padrão
das variáveis
independentes

117. Medidas de Avaliação do Modelo
Likelihood value – quanto mais próximo de zero melhor
Wald Test – medir o grau de significância do modelo
Cox&Snell ou Negelkerk – são pseudos R².

118. Suposições da Regressão Logística
Linearidade
Ausência de autocorrelação
Ausência de correlação entre os resíduos e as variáveis explicativas
Ausência de multicolinearidade

119. Avaliação do Modelo

120. Avaliação do modelo
Como avaliamos se um modelo é bom?
Mais especificamente como comparamos dois modelos?

121. Avaliação do modelo
Acurácia: é a proporção de corretas decisões feita pelo modelo
Acurácia =
𝑁ú𝑚𝑒𝑟𝑜 𝑑𝑒 𝑐𝑜𝑟𝑟𝑒𝑡𝑎 𝑑𝑒𝑐𝑖𝑠õ𝑒𝑠 𝑓𝑒𝑖𝑡𝑎𝑠
𝑇𝑜𝑡𝑎𝑙 𝑑𝑒 𝑑𝑒𝑐𝑖𝑠õ𝑒𝑠 𝑓𝑒𝑖𝑡𝑎𝑠
Taxa de Erro: é a proporção de erradas decisões feita pelo modelo
Erro= 1 -Acurácia

122. Avaliação do modelo
A matriz de confusão permite visualizar a performance do modelo
Verdadeiro positivo (VP): ocorre quando no
conjunto real, a classe que estamos buscando
foi prevista corretamente
Falso positivo (FP): ocorre quando no
conjunto real, a classe que estamos buscando
prever foi prevista incorretamente.
Verdadeiro Negativo (VN): ocorre quando no
conjunto real, a classe que não estamos
buscando prever foi prevista corretamente
Falso negativo (FN): ocorre quando no
conjunto real, a classe que não estamos
buscando prever foi prevista incorretamente.
Previsto
Positivo Negativo
Observado
Positivo
VP FN
Negativo
FP VN

123. Avaliação do modelo
A matriz de confusão permite visualizar a performance do modelo
Acurácia:
𝑉𝑃+𝑉𝑁
𝑉𝑃+𝐹𝑁+𝐹𝑃+𝑉𝑁
Sensibilidade:
𝑉𝑃
𝑉𝑃+𝐹𝑁
Especificidade:
𝑉𝑁
𝐹𝑃+𝑉𝑁
Previsto
Positivo Negativo
Observado
Positivo
VP FN
Negativo
FP VN

124. Avaliação do modelo
Sobre-ajuste ou sobreajuste (overfitting) é um termo usado em
estatística para descrever quando um modelo estatístico se ajusta muito
bem ao conjunto de dados anteriormente observado, mas se mostra
ineficaz para prever novos resultados.
Generalização é a propriedade do modelo de prever dados
que não foram usados para na sua construção.

125. Avaliação do modelo
Construção de modelo com conjunto de dados de treinamento e a
avaliação com um conjuntos de dados de teste.

126. Aula 05 Agrupamento
(Clustering)

127. Definição
A análise de cluster ou agrupamento é uma classe de técnicas usadas para
classificar objetos ou casos em grupos relativamente homogêneos
chamados clusters. Os objetos em cada cluster tendem a ser semelhantes
entre si e diferentes dos objetos nos outros clusters.
Análise de Cluster Não Supervisionada
A ideia é encontrar agrupamentos naturais

128. Exemplo de
Utilização
Segmentação de mercado
Identificação de oportunidades para
novos produtos
Estruturação de departamento
Seleção de mercado teste
Redução de dados

129. Uma situação ideal de agrupamento

130. Uma situação prática de agrupamento

131. Como fazer uma análise de cluster
Seleção dos dados (observações e variáveis)
Seleção de uma medida de distância
Escolher um procedimento de aglomeração
Decidir quanto ao número de clusters
Interpretar e perfilar os clusters
Avaliar a validade do processo de aglomeração

132. Seleção dos dados
▪ Talvez a parte mais importante para agrupamento é selecionar as
variáveis sobre as quais se baseará o procedimento de clusters.
▪ Inclusão de uma ou duas variáveis irrelevantes pode distorcer uma
solução de cluster, de que outra forma, se revelaria útil.
▪ As variáveis devem ser selecionadas com base em resultados passados,
teorias, ou em função das hipóteses que serão testadas. Na mineração não
supervisionada, o analista deve exercer julgamento e aplicar a intuição.

133. Seleção de uma medida de distância
Como o objetivo da aglomeração é agrupar objetos semelhantes, torna-
se necessário uma medida para avaliar quão semelhantes ou diferentes
são os objetos.
A abordagem mais comum consiste em avaliar a semelhança em termos
de distância entre pares de objetos

134. Seleção de uma medida de distância
▪ Distância euclidiana: é a raiz quadrada da soma das diferenças
quadráticas dos valores de cada variável.
▪ Distância de Manhattan (ou city block): entre dois objetos é a soma das
diferenças absolutas nos valores de cada variável.
▪ Distância de Chebychev: entre dois objetos é o valor absoluto da maior
diferença para qualquer variável.

135. Seleção de uma medida de distância

136. Seleção de uma medida de distância
Exemplo do calculo da Distância Euclidiana.

137. Seleção de uma medida de distância
▪ Se as variáveis forem medidas em unidades muito diferentes, a solução
de agrupamento será influenciada pelas unidades de medida. Nesses
casos, antes de agrupar as observações, precisamos padronizar os
dados redimensionando cada variável para ter uma média de zero e um
desvio padrão de unidade. Também é desejável eliminar discrepâncias
(casos com valores atípicos).
▪ O uso de diferentes medidas de distância pode levar a diferentes
resultados de agrupamento. Portanto, é aconselhável usar medidas
diferentes e comparar os resultados.

138. Escolher um procedimento de aglomeração

139. Escolher um procedimento de aglomeração
Método de encadeamento
ÚNICO
MÉDIO
COMPLETO
COSTUMA SER PREFERIDO
ENTRE O MÉTODO DE
ENCADEAMENTO

140. Os métodos de variação tentam gerar clusters
para minimizar a variação dentro do cluster.
O método de Ward é um método de variância
bastante utilizado, em que se deve minimizar
o quadrado da distância euclidiana às médias
dos clusters
O método centroide de variância de
aglomeração em que clusters são gerados a
fiem de maximizar as distância entre os
centroides (distância média para todas as
variáveis) dos clusters.
Dos métodos hierárquicos, o agrupamento
médio e os métodos de Ward têm-se revelado
superiores aos outros métodos.

141. Escolher um procedimento de aglomeração
▪ Não existe um critério categórico.
▪ Uma regra de parada (stopping rule) simples é examinar a distância
entre os grupos a cada passo sucessivo;
▪ Outra regra seria adaptar um teste estatístico de significância;
▪ Além disso, o analista deve confrontar com o referencial teórico, que
pode sugerir um número natural de grupos;
▪ Deve-se, ao final, buscar a melhor solução dentre as possíveis..
Quantos grupos devem ser formados?

142. Decidir quanto ao número de clusters

143. Escolher um procedimento de aglomeração
▪ Limiar sequencial : seleciona um grupo semente e inclui todos os
objetos dentro de uma distância preestabelecida. Após, um novo grupo
semente é selecionado, e o processo continua. Quando um objeto é
destinado a um grupo semente, ele não é mais considerado nos
subsequentes.
▪ Limiar paralelo: seleciona vários grupos semente e inclui todos os
objetos dentro daquele mais próximo. À medida que o processo evolui,
as distâncias podem ser ajustadas para incluir menos ou mais objetos.
▪ Particionamento otimizado: similar aos anteriores, exceto que ele
permite a realocação de objetos em função da maior proximidade com
outro grupo.

144. Escolher um procedimento de aglomeração
Encontrar o melhor centroide

145. Escolher um procedimento de aglomeração
▪ É sugerido que os métodos hierárquicos e não hierárquicos sejam usados
em conjunto. Primeiro, uma solução inicial de aglomeração é obtida
usando um procedimento hierárquico, como ligação média ou Ward. O
número de clusters e centroides de cluster assim obtidos é usado como
entrada para o método de particionamento otimizado.
▪ A escolha de um método de agrupamento e a escolha de uma medida de
distância estão interrelacionadas. Por exemplo, distâncias euclidianas
quadradas devem ser usadas com os métodos de Ward e centroide. Vários
procedimentos não hierárquicos também usam distâncias euclidianas
quadradas.

146. Interpretar e perfilar os clusters
▪ Envolve o exame de cada grupo, tendo em vista o conjunto de variáveis,
para denominar ou atribuir uma identificação que descreva
adequadamente a natureza dos mesmos.
▪ Para esse processo, podem ser utilizados escores, de modo a identificar
alguma hierarquia dentre os mesmos.
▪ Nessa fase, o analista deve comparar os resultados com aqueles
propostos anteriormente pela experiência prática.

147. Interpretar e perfilar os clusters
▪ A interpretação e criação de perfil de clusters envolve a análise dos
centroides do cluster. Os centroides nos permitem descrever cada
cluster, atribuindo-lhe um nome ou rótulo.
▪ Geralmente, é útil criar um perfil dos clusters em termos de variáveis que
não foram usadas para cluster. Isso pode incluir dados demográficos,
psicográficos, uso de produtos, uso de mídia ou outras variáveis

148. Interpretar e perfilar os clusters

149. Avaliar a validade do processo de aglomeração
▪ Alguns procedimentos de validação da solução:
1) dividir a amostra em dois grupos;
2) usar outras variáveis conhecidas por discriminar entre os grupos, ou
refazer a análise excluindo algumas variáveis;
3) refazer a análise utilizando outros métodos de agrupamento e outras
medidas de similaridade

150. OUTRAS TECNICAS DE ANÁLISE DE DADOS

151. Dados são mais do que apenas números

152. TÉCNICAS AVANÇADAS

153. TÉCNICAS AVANÇADAS
Como o Google consegue identificar gatos nas minha fotos?

154. TÉCNICAS AVANÇADAS
Deep learning é uma nova área do marchine
learning que utiliza redes neurais artificiais para não
supervisionado para reconhecimento de padrões
Deep Learning está sendo utilizando em diferentes
campos:
▪ Reconhecimento de objetos
▪ Reconhecimento de voz
▪ Descoberta de drogas

155. ▪ O perceptron é um algoritmo para
aprendizagem supervisionada de
classificação binária.
▪ Similar a regressão logística
▪ Pode ser usado para aprendizagem
online

156. ▪ Redes neurais podem aproximar
qualquer função.
▪ Os pesos são atualizados usando um
algoritmo chamado backpropagation

157. ▪ Entrada e saída são a mesma imagem - uma percepção por pixel
▪ Camadas ocultas têm menos percepções
▪ Cada percepção em uma camada oculta deve representar um conceito mais elaborado
▪ Os recursos são criados automaticamente: não há necessidade de defini-los manualmente
Deep learning consiste em treinar uma rede neural em
que os inputs e outputs são os mesmo

158. A rede neural (treinada) pode ser usada para classificação
▪ A rede pode ser dividida ao meio e pode ser usada para classificação após o treinamento
▪ Perceptrons nas camadas ocultas podem ser facilmente rotulados

159. Redes neurais foi desenvolvido em torno do ano
de 1950
▪ Grande quantidades de dados à disposição
▪ Possibilidade de utilizar 1.0000 maquinas para resolver um simples
problema.
Google utilizar cerca de 16.000 processadores para criar uma rede neural com
mais de um bilhão de conexões.
Deep learning é relativamente um método antigo
Por que agora?

160. MUITO OBRIGADO!
luizalvesadm@gmail.com
(85) 987796426