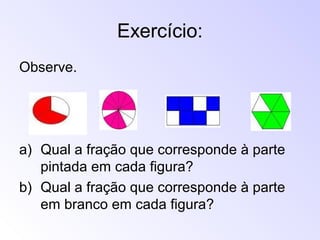
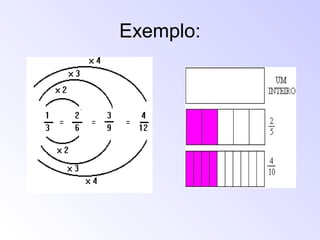
1) As frações surgiram no antigo Egito para marcar terras ao longo do rio Nilo, já que as inundações apagavam as marcações. 2) Os egípcios dividiam as terras em partes iguais usando cordas e criaram frações unitárias como 1/2 e 1/3 para descrever as porções. 3) Frações são usadas para fornecer medidas mais precisas quando números inteiros não são suficientes.

1. Frações

2. Um pouco de história ...
O estudo de frações surgiu no Egito às
margens do rio Nilo, pela necessidade de se
realizar a marcação das terras que se
encontravam a margem do mesmo. No período
de junho a setembro, o rio inundava essas
terras, levando parte da marcação. Logo, os
proprietários destas terras tinham que remarcá-
las. A marcação destas terras era realizada
pelos geômetras dos faraós, que utilizavam
cordas como unidade de medida, denominados
estiradores de cordas.

3. A marcação era realizada da seguinte maneira:
Esticava-se as cordas e assim se observava quantas vezes
aquela unidade de medida estava contida no terreno. Como
a medida dos terrenos, na sua maioria, não era dada
exatamente por números inteiros, surgia
então a necessidade de um novo conceito
de número, o número fracionário.
Os egípcios usavam frações unitárias,
ou seja, com o numerador um dividido
por um número inteiro, como por exemplo:
½, 1/3, ¼, ...
Eram denominadas frações egípcias.

4. Os números fracionários ou
simplesmente frações
surgiram da necessidade
de dar uma resposta mais
precisa para uma medida.

5. Observe a situação
envolvendo fração:
Para o logotipo de uma empresa, a idéia inicial
surgiu de uma folha de papel sulfite
dividida em 4 partes de mesmo
tamanho com uma parte delas
pintadas de vermelho.
A parte pintada representa qual fração do
logotipo?
Representa a fração 1 .
4

7. Numerador e denominador são os
nomes dos termos de uma fração:
1 → numerador
4 → denominador
Os números fracionários como ¼, ½, ¾,
são chamados de frações.

8. Exercício:
Observe.
a) Qual a fração que corresponde à parte
pintada em cada figura?
b) Qual a fração que corresponde à parte
em branco em cada figura?

9. Leitura das frações
• → dois terços
• → nove doze avos
• → cinco oitavos
• → cinco sextos

10. Frações Equivalentes
Frações equivalentes são frações que
representam a mesma parte do todo.
• Exemplo: 1 , 2 , 4 são equivalentes
2 4 8
Para encontrar frações equivalentes devemos
multiplicar o numerador e o denominador por
um mesmo número natural, diferente de zero.

11. Exemplo: