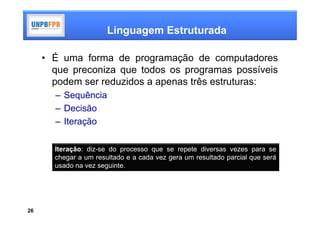
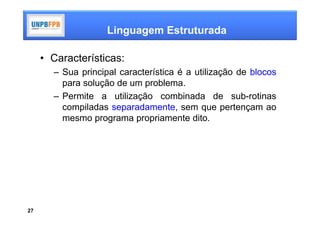
O documento discute conceitos e técnicas de programação. Aborda lógica de programação, incluindo álgebra de proposições, algoritmos e linguagem estruturada. Explica como algoritmos podem ser usados para resolver problemas de forma estruturada através de sequências, decisões e iterações.

1. Gestão de Tecnologia da Informação
Conceitos e Técnicas de
Programação
Profº Ms. Tarcísio Júnior
1

2. um pouco
de filosofia Raciocínio Lógico, todos tem, poucos usam !
Às vezes, basta você
parar e raciocinar.
Logo perceberá que a
resposta está com
você o tempo todo.
2

3. Conceitos e Técnicas de Programação
Lógica de
programação
3

4. Álgebra das proposições
A lógica está relacionada com o pensamento e é de grande
interesse saber-se como é possível automatizar algumas
maneiras de pensar.
No século XIX, George Boole desenvolveu um sistema de
álgebra (a álgebra das proposições), onde se poderia
determinar se uma sentença é falsa ou verdadeira.
Em 1930, Alan Turing mostrou que com a álgebra de Boole
apenas três funções lógicas são necessárias para o processo
de determinação do FALSO ou VERDADEIRO.
Estas funções são: E, OU, NÃO.
4

5. Álgebra das proposições
Chama-se proposição qualquer afirmação verbal da qual se
possa dizer que é falsa ou verdadeira.
Assim, “choveu ontem à tarde” é uma proposição, pois pode
ser falsa ou verdadeira, mas, “onde é que você esteve?” não
é uma proposição, pois não se pode dizer que é falsa ou
verdadeira.
5

6. Álgebra das proposições
Duas proposições podem ser combinadas pelo conectivo E para formar uma
proposição chamada conjunção das proposições originais. A conjunção das
proposições p e q representa-se por:
⋀ lê-se p e q
A conjunção de duas proposições é verdadeira se e somente se ambas as
proposições são verdadeiras.
Sejam as seguintes proposições:
p: Paris está na França;
q: Paris está na Inglaterra;
r: 2 + 2 = 5;
s: 2 + 2 = 4.
Qual será o valor lógico (falso, verdadeiro) das conjunções:
a ⋀
b ⋀
c ⋀
d ⋀
6

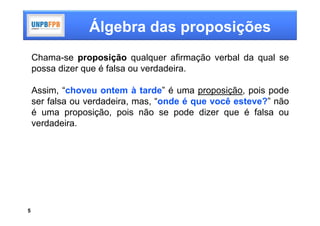
7. Álgebra das proposições
onde: p: Paris está na França;
q: Paris está na Inglaterra;
r: 2 + 2 = 5;
s: 2 + 2 = 4.
respondendo:
a ⋀ Paris está na França (p) e 2 + 2 = 4 (s) [ verdade ]
b ⋀ Paris está na França (p) e 2 + 2 = 5 (r) [ falso ]
c ⋀ Paris está na Inglaterra (q) e 2 + 2 = 4 (s) [ falso ]
d ⋀ Paris está na Inglaterra (q) e 2 + 2 = 5 (r) [ falso ]
portanto: p q pΛq
V V V
V F F
F V F
F F F
7

8. Álgebra das proposições
Duas proposições quaisquer podem ser combinadas pelo conectivo OU para formar
uma nova proposição chamada disjunção das proposições originais. A disjunção de
duas proposições p e q é designada por:
lê-se p ou q
A disjunção de duas proposições é verdadeira se e somente se, pelo menos, uma
delas for verdadeira.
Usando as proposições do exemplo anterior:
p: Paris está na França;
q: Paris está na Inglaterra;
r: 2 + 2 = 5;
s: 2 + 2 = 4.
Qual será o valor lógico (falso, verdadeiro) das disjunções:
a ⋁
b ⋁
c ⋁
d ⋁
8

9. Álgebra das proposições
onde: p: Paris está na França;
q: Paris está na Inglaterra;
r: 2 + 2 = 5;
s: 2 + 2 = 4.
respondendo:
a ⋁ Paris está na França (p) ou 2 + 2 = 4 (s) [ verdade ]
b ⋁ Paris está na França (p) ou 2 + 2 = 5 (r) [verdade ]
c ⋁ Paris está na Inglaterra (q) ou 2 + 2 = 4 (s) [verdade ]
d ⋁ Paris está na Inglaterra (q) ou 2 + 2 = 5 (r) [ falso ]
portanto: p q p⋁q
V V V
V F V
F V V
F F F
9

10. Exercício
Usando a convenção 1 para verdadeiro e 0 para falso, completar a tabela a seguir:
p q p ∧ ┐q p ⋁ ┐q
1 1
1 0
0 1
0 0
Resposta:
p q p ∧ ┐q p ⋁ ┐q
1 1 1 e 0 = 0 [V e F = F] 1 ou 0 = 1 [V e F = V]
1 0 1 e 1 = 1 [V e V = V] 1 ou 1 = 1 [V e V = V]
0 1 0 e 0 = 0 [F e F = F] 0 ou 0 = 0 [F e F = F]
0 0 0 e 1 = 0 [F e V = F] 0 ou 1 = 1 [F e V = V]
10

11. Algoritimizando a Lógica
• Construir algoritmos é o objetivo fundamental de toda a
programação, mas afinal o que é algoritmo?
– Algoritmo é uma sequência de passos que visam atingir
um objetivo bem definido.
– Algoritmo é a descrição de um conjunto de ações que
obedecidas, resultam numa sucessão finita de passos,
atingindo o objetivo.
– Descrição de um conjunto finito de instruções para a
solução de um problema em um tempo finito.
11

12. Conceito
Algoritmo é a descrição de um conjunto de
comandos que, obedecidos, resultam numa sucessão
finita de ações (FARRE et al., 1999).
Uma simples ação como escovar os dentes pode ser
descrita, de modo a formar o que chamamos de
Algoritmo.
12

13. Conceito
Veja o exemplo de um algoritmo composto pelos passos necessários para escovar
os dentes.
Escovar os Dentes:
INÍCIO ou INÍCIO DO ALGORITMO
1.Pegue a escova de dentes;
2.Pegue o creme dental com a outra
mão;
3.Coloque creme dental na escova;
4.Coloque a escova na boca e escove
os dentes e a língua;
5.Tire a escova da boca;
6.Lave a boca e a escova com água.
FIM ou FIM DO ALGORITMO
13

14. Algoritimizando a Lógica
• Podemos pensar em algoritmo como uma receita, uma
sequência de instruções que dão cabo de uma meta
específica.
• Estas tarefas não podem ser redundantes nem
subjetivas na sua definição, devem ser claras e precisas.
• Por quê isso?
14

15. Algoritimizando a Lógica
• Pessoas tem inteligência e habilidade racional
– fazem perguntas para se esclarecer.
• Computador não tem senso próprio
– deve receber instruções explícitas (algoritmos)
15

16. Algoritmo
Um algoritmo poderia ser grosseiramente comparado a
uma receita culinária:
– Uma receita é um programa de atividades que deve ser
respeitada e cumprida passo-a-passo.
– Caso um dos passos seja desconsiderado, a receita não
dará certo.
Como preparar um bolo?
Em um livro de receitas,
encontramos processo
semelhante à descrição seguinte
para fazer um bolo.
16

17. Algoritmo
Passos necessários para fazer um bolo de cenouras:
Ingredientes: Modo de preparo:
- Massa: 1. Bata as cenouras no liquidificador, com os ovos
1/2 xícara (chá) de óleo; e o óleo. Então, acrescente o açúcar e bata por
3 cenouras médias raladas; mais 5 minutos;
4 ovos; 2. Em uma tigela ou batedeira, misture o restante
2 xícaras (chá) de açúcar; dos ingredientes, exceto o fermento;
2 1/2 xícaras (chá) de farinha de trigo; 3. Misture o fermento lentamente, com uma
1 colher (sopa) de fermento em pó. colher;
4. Asse em forno pré-aquecido (180ºC) por 40
- Cobertura: minutos;
1 colher (sopa) de manteiga; 5. Para a cobertura, misture todos os
3 colheres (sopa) de chocolate em pó; ingredientes, leve ao fogo e faça uma calda,
1 xícara (chá) de açúcar. que será adicionada à massa já assada.
Note que o modo de preparo é um conjunto de passos definidos que devem ser
seguidos rigorosamente em ordem e que se utilizam dos itens listados no conjunto de
ingredientes.
É puramente um algoritmo! Em um programa de computador, o modo de preparo
corresponde às instruções usadas para manipular os ingredientes, isto é, são os
dados.
17

18. Algoritmo
Um algoritmo não representa, necessariamente, um
programa de computador, e sim os passos
necessários para realizar uma tarefa.
• Algoritmo não é a solução do
problema, pois, se assim fosse,
cada problema teria um único
algoritmo.
• Algoritmo é um caminho para a
solução de um problema.
– Em geral, os caminhos que levam
a uma solução são muitos.
18

19. Algoritmo Não Computacional
• Podemos criar algoritmos para tarefas do cotidiano.
Ex: Algoritmo não computacional cujo objetivo é usar um
telefone público.
19

20. Algoritmo Não Computacional
20

21. Algoritmo
• Outro exemplo: algoritmo para “somar 2 números
quaisquer” usando a notação abaixo.
– Escreva o primeiro número no retângulo A
– Escreva o primeiro número no retângulo B
– Some o número do retângulo A com número do
retângulo B e coloque o resultado no retângulo C
21

22. Exercício
Faça um algoritmo para somar dois números e multiplicar
o resultado pelo primeiro número:
Resolução:
• Receba o valor do numero 1
• Receba o valor do numero 2
• Some todos os itens
• Multiplique o resultado pelo valor do número 1
•Escreva o resultado
22

23. Por que usar algoritmos?
• Abstração - todo o esforço é concentrado na resolução
do problema e não em detalhes computacionais que
podem ser acrescentados posteriormente.
• Portabilidade - uma solução algorítmica pode ser
traduzida para qualquer linguagem de programação.
23

24. Programas
• Os programas de computadores nada mais são
do que algoritmos escritos numa linguagem de
computador (Pascal, C, Cobol, Fortran, Visual
Basic, Java, dentre outras) e que são
interpretados e executados por um computador.
24

25. Programas
• Aprender uma linguagem de programação sem
dominar a criação de algoritmos não faz sentido,
seria o mesmo que ter um vocabulário vasto, mas
não saber usar as palavras certas na hora certa.
• Sabendo algoritmo é relativamente fácil criar um
programa em qualquer linguagem, basta pesquisar
qual comando realiza a ação desejada.
25

26. Linguagem Estruturada
• É uma forma de programação de computadores
que preconiza que todos os programas possíveis
podem ser reduzidos a apenas três estruturas:
– Sequência
– Decisão
– Iteração
Iteração: diz-se do processo que se repete diversas vezes para se
chegar a um resultado e a cada vez gera um resultado parcial que será
usado na vez seguinte.
26

27. Linguagem Estruturada
• Características:
– Sua principal característica é a utilização de blocos
para solução de um problema.
– Permite a utilização combinada de sub-rotinas
compiladas separadamente, sem que pertençam ao
mesmo programa propriamente dito.
27

28. Passos para elaboração de um programa
1. Compreender o problema;
2. Esboçar um procedimento para resolver o problema;
3. Formular o algoritmo;
4. Traduzir o algoritmo para uma linguagem de
programação (codificação).
28

29. só para
descontrair
29