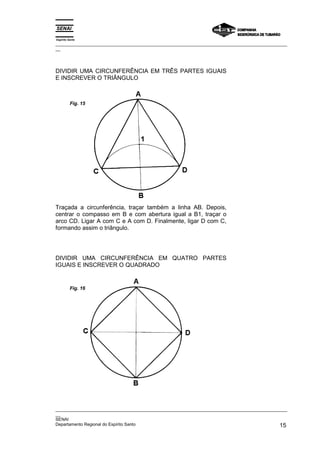
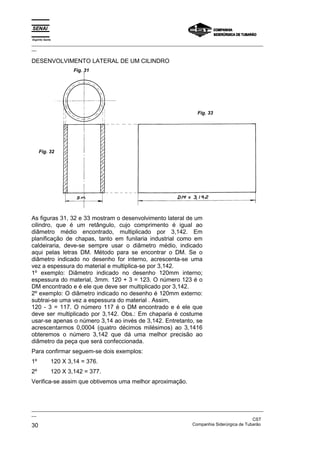
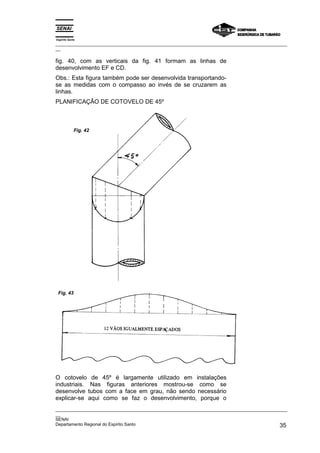
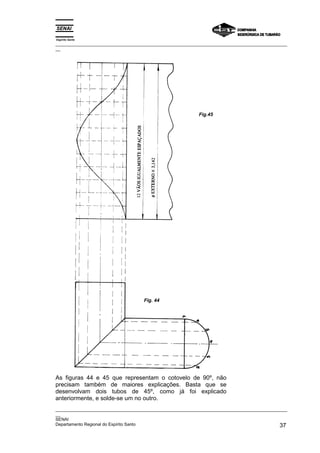
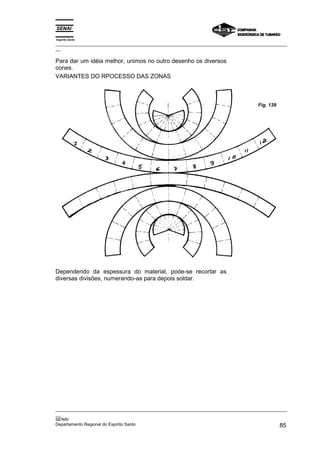
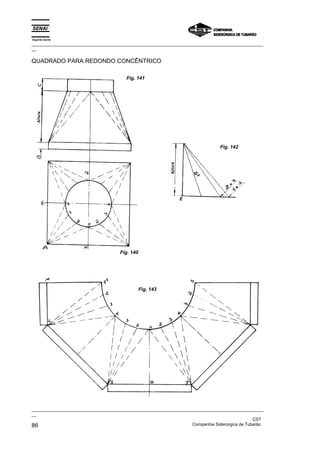
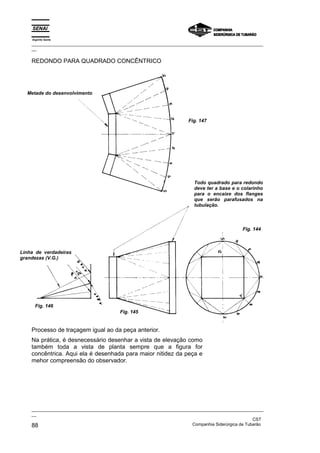
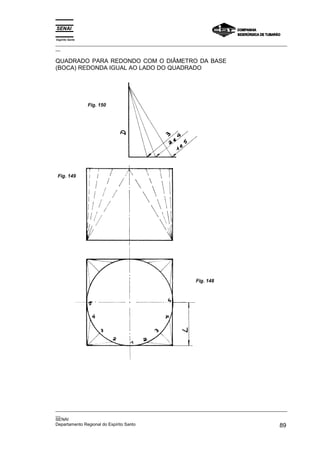
Este documento fornece instruções detalhadas sobre como traçar vários elementos geométricos como retas, ângulos, paralelas, perpendiculares e circunferências. Ele também mostra como dividir essas figuras em partes iguais e inscrever figuras geométricas dentro delas, como triângulos, quadrados e pentágonos. O documento foi elaborado pelo SENAI e CST para fins educacionais de programação de caldeiraria.