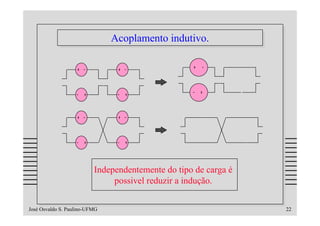
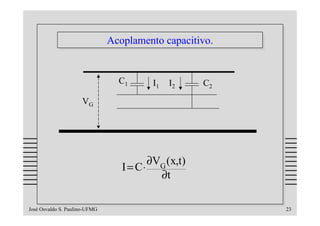
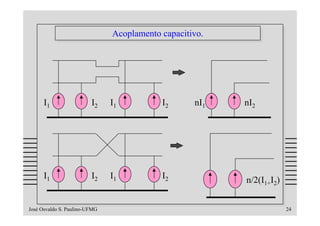
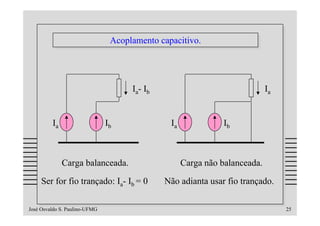
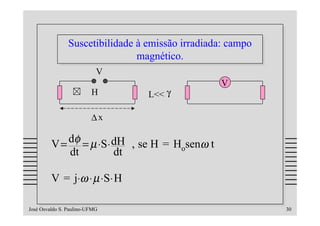
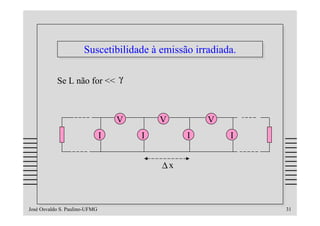
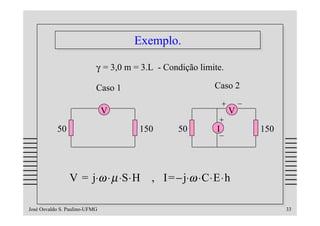
O documento discute os problemas de indução em cabos e linhas causados por campos elétricos e magnéticos, apresentando modelos matemáticos e exemplos numéricos. Aborda temas como impedância de transferência, blindagens, acoplamentos indutivo e capacitivo e formas de reduzir a indução através do uso de técnicas como transposição, terminações balanceadas e mudança do tipo de cabo.

1. Indução em
Indução em
cabos e linhas
cabos linhas
(Estudo Técnico 6: Indução de baixa
(Estudo Técnico 6: Indução de baixa
freqüência em cabos coaxiais.)
freqüência em cabos coaxiais.)
José Osvaldo S. Paulino-UFMG 1

2. “Crosstalk”: problema geral..
“Crosstalk”: problema geral
x
Rs
IG(x,t)
VG(x,t)
V(t) RL
IR(x,t)
VNE(t) RNE VR(x,t) RFE VFE(t)
IR(x,t)+ IG(x,t)
VNE(t) e VFE(t) ?
José Osvaldo S. Paulino-UFMG 2

3. Dificuldades:
Modelagem do circuito;
Cálculo dos parâmetros.
Facilidades: Resolução do circuito.
Programas computacionais:
PSPICE;
MICROTRAN.
José Osvaldo S. Paulino-UFMG 3

4. Exemplo: placa de circuito impresso.
Exemplo: placa de circuito impresso.
José Osvaldo S. Paulino-UFMG 4

5. Exemplo: placa de circuito impresso.
Exemplo: placa de circuito impresso.
José Osvaldo S. Paulino-UFMG 5

6. Exemplo: Rede telefônica.
Exemplo: Rede telefônica.
Fase A
Fase B
Fase C
Neutro
Aterramento Aterramento Aterramento
do protetor da blindagem do neutro
José Osvaldo S. Paulino-UFMG 6

7. Exemplo: Indução dentro da própria edificação.
Exemplo: Indução dentro da própria edificação.
José Osvaldo S. Paulino-UFMG 7

8. Tensões longitudinais (modo comum)
Tensões longitudinais (modo comum)
e transversais (metálicas).
e transversais (metálicas).
Rs
V(t) V12
V2
V1
José Osvaldo S. Paulino-UFMG 8

9. Cabos blindados.
Cabos blindados.
Rs
RNE
VNE(t) RL
RFE VFE(t)
José Osvaldo S. Paulino-UFMG 9

10. Impedância de transferência.
Impedância de transferência.
Ei IG
Hi
Vt
IB VB
José Osvaldo S. Paulino-UFMG 10

11. Impedância de transferência.
Impedância de transferência.
Eint = Zt1 . IB
r
L
Vt = Eint . L
Vt = Zt . IB
Eint Vt
Zt - ohms/metro
µ,σ T
IB
José Osvaldo S. Paulino-UFMG 11

12. Impedância de transferência:
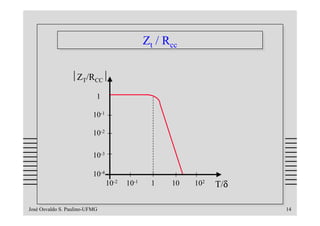
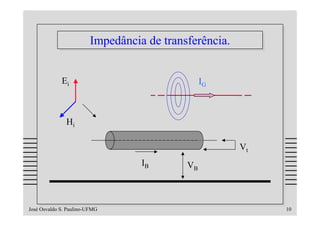
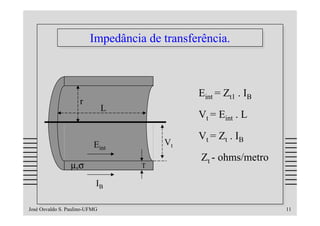
Impedância de transferência:
Deduzido por Schelkunoff.
Deduzido por Schelkunoff.
(1+ j) ⋅ T
Z = 1 ⋅ δ , T<< a << λ
t 2πrσT sinh[(1+ j) T ]
δ
δ= 1 ⇒ Profundidade de penetracao
πfµσ
r ⇒ raio da blindagem , T ⇒ Espessura.
José Osvaldo S. Paulino-UFMG 12

13. Impedância de transferência.
Impedância de transferência.
T << 1 ⇒ Z ≈ 1 = R
δ t 2πaσT cc
−T
T >> 1 ⇒ Z ≈ 2 ⋅ 2 ⋅e δ ⋅ R
δ t hf
R hf = 1
2πaσδ
José Osvaldo S. Paulino-UFMG 13

14. Ztt // Rcc
Z Rcc
ZT/RCC
1
10-1
10-2
10-3
10-4
10-2 10-1 1 10 102 T/δ
José Osvaldo S. Paulino-UFMG 14

15. Exercício.
Exercício.
ID= 10 kA
ID/2 ID/2
Vt
L
Dados: VB
VB, Vt = ? R
R = 30 Ohms;
Zcabo = 400 Ohms, L = 2 km;
Zt = Rcc = 2 x 10 -4 Ohms/metro.
José Osvaldo S. Paulino-UFMG 15

16. Blindagens reais.
Blindagens reais.
Muito difícil calcular a impedância !
Solução: Medição
José Osvaldo S. Paulino-UFMG 16

17. Mudança de tipo de cabo.
Mudança de tipo de cabo.
Vt1 << Vt << VB
Vt VB1 = VB+Vt = VB
Vt1
IB
R VB
VB1
José Osvaldo S. Paulino-UFMG 17

18. Aberturas, emendas e terminações.
Aberturas, emendas e terminações.
0,5 m
S
V
IB IB IB
IB dIB/dt = 5 kA/us
S L = 0,5 uH
V = L.dI/dt + Zt.IB = 2,5 kV + Vt = 2,5 kV
José Osvaldo S. Paulino-UFMG 18

19. Cabo com dupla blindagem.
Cabo com dupla blindagem.
Zt
Zt1
Vt1
IB1 Vt
IB
Vt = IB . Zt
Para baixas frequências:
Vt1 = IB1 . Zt1
Zeq = (R.R1)/(R+R1)
Vt1 << Vt
José Osvaldo S. Paulino-UFMG 19

20. Par trançado: transposição.
Par trançado: transposição.
IG
Rs
VG V1 V2 RL
José Osvaldo S. Paulino-UFMG 20

21. Acoplamento indutivo.
Acoplamento indutivo.
IG
B A
dl
S V
dl
v = ∫ E⋅ dl = ∫∫ ∂B⋅ ds = ∫ ∂A ⋅ dl
s s ∂t s ∂t
José Osvaldo S. Paulino-UFMG 21

22. Acoplamento indutivo.
Acoplamento indutivo.
Independentemente do tipo de carga é
possivel reduzir a indução.
José Osvaldo S. Paulino-UFMG 22

23. Acoplamento capacitivo.
Acoplamento capacitivo.
C1 I1 I2 C2
VG
∂VG (x,t)
I = C⋅
∂t
José Osvaldo S. Paulino-UFMG 23

24. Acoplamento capacitivo.
Acoplamento capacitivo.
I1 I2 I1 I2 nI1 nI2
I1 I2 I1 I2 n/2(I1+I2)
José Osvaldo S. Paulino-UFMG 24

25. Acoplamento capacitivo.
Acoplamento capacitivo.
Ia- Ib Ia
Ia Ib Ia Ib
Carga balanceada. Carga não balanceada.
Ser for fio trançado: Ia- Ib = 0 Não adianta usar fio trançado.
José Osvaldo S. Paulino-UFMG 25

26. Terminações balanceadas.
Terminações balanceadas.
Transformador
José Osvaldo S. Paulino-UFMG 26

27. Suscetibilidade à emissão irradiada.
Suscetibilidade à emissão irradiada.
L
RS s Ey Hz RL
V S, V L = ?
José Osvaldo S. Paulino-UFMG 27

28. Suscetibilidade à emissão irradiada: campo
Suscetibilidade à emissão irradiada: campo
elétrico.
elétrico.
E E
∆x
V
V
V
V = ∫ E ⋅ dl
José Osvaldo S. Paulino-UFMG 28

29. Suscetibilidade à emissão irradiada: campo
Suscetibilidade à emissão irradiada: campo
elétrico.
elétrico.
V C
L
I = C dV , se E = Eosenω t
I dt
I= -j⋅ω ⋅ C ⋅ V = − j⋅ω ⋅ C ⋅ E ⋅ h
L<< γ
José Osvaldo S. Paulino-UFMG 29

30. Suscetibilidade à emissão irradiada: campo
Suscetibilidade à emissão irradiada: campo
magnético.
magnético.
V
V
H L<< γ
∆x
V= dφ = µ ⋅S⋅ dH , se H = H senω t
o
dt dt
V = j⋅ω ⋅ µ ⋅S⋅ H
José Osvaldo S. Paulino-UFMG 30

31. Suscetibilidade à emissão irradiada.
Suscetibilidade à emissão irradiada.
Se L não for << γ
V V V
I I I I
∆x
José Osvaldo S. Paulino-UFMG 31

32. Exemplo.
Exemplo.
RS H h H
E RL E
L
Caso 1 Caso 2
L = 1,0 m E = 10 V/m RS =50 Ohms RL=150 Ohms
f = 100 MHz h = 1,27 mm r = 0,19 mm
José Osvaldo S. Paulino-UFMG 32

33. Exemplo.
Exemplo.
γ = 3,0 m = 3.L - Condição limite.
Caso 1 Caso 2
V V
50 150 50 I 150
V = j⋅ω ⋅ µ ⋅S ⋅ H , I = − j⋅ω ⋅ C ⋅ E ⋅ h
José Osvaldo S. Paulino-UFMG 33

34. Exemplo.
Exemplo.
π ⋅ε o ⋅ε r
H= E = E , C= (F/ m)
η o 120⋅π ln( h )
r
C = 14,64 pF/ m
V = j⋅ 26,6 mV , I = - j⋅ 0,1168 mA
Caso 1 : VS = j6,65 mV , VL = -j20 mV
Caso 2 : VS = j11,03 mV , VL = -j15,62 mV
José Osvaldo S. Paulino-UFMG 34