Aula 3 e 4.pdf

Elementos de Máquinas II
ELEMENTOS DE MÁQUINAS II
Curso: Engenharia Mecânica
Professor: Me. Douglas Costa Eiriz
1º semestre 2023
1 / 34

Dimensionamento de Engrenagens
O dimensionamento de engrenagens é um tema fundamental para a engenharia
mecânica e é de grande importância para a indústria. O objetivo principal do
dimensionamento de engrenagens é garantir que as engrenagens possam
transmitir a potência e a velocidade necessárias para o funcionamento do sistema
mecânico de forma eficiente e segura.
2 / 34

Fundamentos do Engrenamento
Circunferências de referência (primitivas)
Diâmetros de referência (primitivos)
Ponto de referência (primitivo)
Lei Fundamental de Engrenamento: Razão de velocidades mv deve manter-se
constante durante o engrenamento.
mv =
ωext
ωint
= ±
rint
rext
3 / 34

Fundamentos do Engrenamento
Razão de torque ou Ganho mecânico
ma =
1
mv
Razão de engrenamento
mg = |mv| ou mg = |ma|, para mg ≥ 1
4 / 34

A Forma Involuta do Dente
A linha está sempre tangente ao
círculo de base
O centro de curvatura da involuta
está sempre em um ponto de
tangência da linha com o círculo de
base
Uma tangente à involuta é sempre
normal à linha, que é o raio
instantâneo de curvatura da curva
involuta
5 / 34

Geometria de contato e ângulo de pressão dos dentes
6 / 34

Circunferência de base: São os cilindros de onde as linhas da cuva involuta
são desenroladas. É necessariamente menor que a circunferência de
referência.
Na circunferência primitiva (ou de referência) estão os raios primitivos, e o
dente da engrenagem deve ser projetado abaixo e acima desta curva.
Adendo é a parte do dente que está acima da linha primitiva e dedendo é
parte que está abaixo da linha.
Linha de ação ou normal comum: Sempre passa pelo ponto de referência
primitivo tangenciando as circunferências de base.
Há uma tangente comum a ambas as involutas do dente no ponto de contato,
e está é perpendicular à normal comum.
O ponto primitivo tem a mesma velocidade linear no pinhão e na engrenagem,
chamada de velocidade de linha de referência (primitiva).
7 / 34

Ângulo de Pressão ϕ: Medido entre a linha de ação e o vetor velocidade.
Medido sempre na direção na engrenagem movida.
Os ângulos de pressão do par de engrenagens são padronizados pelos
fabricantes de engrenagens a uns poucos valores.
Os valores padronizados são 14,5°, 20° e 25°, sendo 20° o valor mais
comumente usado e 14,5, obsoleto hoje em dia.
As engrenagens podem ser feitas com qualquer ângulo de pressão, mas o
custo comparado ao custo das engrenagens padronizadas dificilmente se
justificaria.
8 / 34

9 / 34

A distância ao longo da linha de ação entre os pontos contato de entrada e de
saída, dentro do engrenamento, é chamada de comprimento de ação Z.
Z =
q
(rp + ap)2 − (rpcosϕ)2 +
q
(rg + ag)2 − (rgcosϕ)2 − Csenϕ
Onde rp e rg são os raios primitivos e ap e ag são as medidas dos adendos. C é a
distância entre centros e ϕ é o ângulo de pressão.
10 / 34

Relações de Transmissão Indicadas
11 / 34

Características do Dente
12 / 34

Características Geométricas (DIN 862 e 867)
13 / 34

Características Geométricas (DIN 862 e 867)
14 / 34

Diâmetros Principais
Diâmetro primitivo (ou de referência): do = m.Z
Diâmetro de base: dg = do.cosα
Diâmetro interno (pé do dente): df = do − 2hf
Diâmetro externo (cabeça do dente): dk = do + 2hk
15 / 34

Formulário (DIN 862 e 867)
16 / 34

Formulário (DIN 862 e 867)
17 / 34

Critérios de Dimensionamento
1 Critério de desgaste (de resistência à pressão);
2 Critério de resistência à flexão no pé do dente.
18 / 34

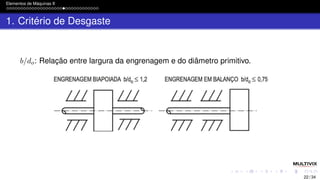
1. Critério de Desgaste
Material Aço: Considerando angulo de pressão α = 20o e número de dentes de 18
a 40.
b1.do1
2
= 5, 72.105.
MT
P2
adm
.
i ± 1
i ± 0, 14
.ϕ
± - engrenamento externo (+) interno (-)
b1 - largura do dente do pinhão [mm]
do1 - diâmetro primitivo do pinhão [mm]
MT - momento torsor no pinhão [Nmm]
Padm - Pressão admissível [MPa (N/mm2)]
i - relação de transmissão
ϕ - fator de serviço (consultar tabela)
19 / 34

Pressão Admissível
Padm =
0, 487.HB
W1/6
Fator de Durabilidade
W =
60.np.H
106
Em que:
np - rotação do pinhão [rpm]
H - duração do par [horas]
HB - dureza Brinell [N/mm2]
20 / 34

Tabela de Dureza Brinell
21 / 34

b/do: Relação entre largura da engrenagem e do diâmetro primitivo.
22 / 34

Normalização do Módulo
Ao estimar o módulo, se por exemplo
ele se encontrar entre 1,0 e 4,0 mm,
os módulos normalizados serão: 1,0;
1,25; 1,5; 1,75;... 3,5; 3,75; 4,0.
23 / 34

2. Critério de Resistência à Flexão no Pé do Dente
Somente o dimensionamento ao critério de desgaste não é insuficiente para
projetar a engrenagem. É necessário que seja verificada a resistência à flexão no
pé do dente. A engrenagem estará apta a suportar os esforços da transmissão
quando a tensão atuante no pé do dente for menor ou igual à tensão admissível do
material indicado.
24 / 34

Força Tangencial: O vetor ⃗
Ft aponta a mesma direção da velocidade tangencial.
Ft =
MT
ro
=
2MT
do
Em que:
Ft - força tangencial [N]
MT - torque [Nmm]
ro - raio primitivo [mm]
do - diâmetro primitivo [mm]
25 / 34

Força Radial: Atua na direção radial da engrenagem
Fr = Ft.tgα
Força resultante: Atua na direção radial da engrenagem
Fn =
q
Ft
2
+ Fr
2
Fn =
Ft
cosα
Fn =
Fr
senα
As cargas radial e resultante são importantes no dimensionamento de eixos e
mancais, não sendo necessárias no dimensionamento das engrenagens.
26 / 34

Tensão de Flexão no Pé do Dente
A tensão atuante no pé deve ser menor ou igual à tensão admissível do material
σmax =
Ft.q.ϕ
b.m
≤ σmaterial
Em que:
σmax - tensão máxima atuante na base do dente. [N/mm2]
ϕ - fator de serviço (tabela AGMA)
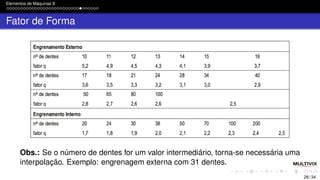
q - fator de forma (adimensional)
σmaterial - tensão admissível do material. [N/mm2]
27 / 34

Fator de Forma
Obs.: Se o número de dentes for um valor intermediário, torna-se necessária uma
interpolação. Exemplo: engrenagem externa com 31 dentes.
28 / 34

Tensão Admissível
O projeto ideal é aquele em que a tensão atuante no pé do dente está bem
próxima da tensão admissível no seu limite inferior.
Se a tensão atuante estiver acima da admissível, a engrenagem pode não
suportar a transmissão, e se romper na base do dente prematuramente.
Se a tensão atuante estiver bem aquém da tensão admissível, a engrenagem
estará superdimensionada, tornando-se antieconômica. 29 / 34

Procedimento de Dimensionamento
No dimensionamento de um par de engrenagens, o pinhão (engrenagem menor) é
o dimensionado, pois se ele resistir ao esforço aplicado, a coroa (engrenagem
maior) suporta com folga a mesma carga.
1. Critério de Pressão (desgaste)
Torque no pinhão MT
Relação de transmissão i
Pressão admissível Padm e Fator de durabilidade W
Fator de serviço ϕ
Volume mínimo do pinhão b.do
2
= x
Módulo do engrenamento m (normalizado)
Diâmetro primitivo do (recalculado)
Largura do pinhão b1
30 / 34

Procedimento de Dimensionamento
2. Critério de resistência à flexão no pé do dente
Tensão máxima no pé do dente σmax
Força tangencial Ft
Fator de forma q
Fator de serviço ϕ
Módulo normalizado m
Largura do pinhão b
Tensão máxima atuante no pé do dente σmax
Análise do dimensionamento
31 / 34

Exercícios
1. Dimensionar o par de engrenagens cilíndricas de dentes retos (ECDR), para que
possa atuar com segurança na transmissão representada a seguir.
Dados: A transmissão será acionada por um motor P=15CV(≈11 kW) com uma
rotação de 1140 rpm. O material será SAE 4340. A dureza específica é 58 HCR,
duração prevista de 10000h. Tempo de serviço máximo de 10h diárias.
Considere:
b1/do1 = 0, 25
α = 20
Z1 = 29
Z2 = 110
32 / 34

Exercícios
2. Dimensionar o par de engrenagens cilíndricas de dentes retos (ECDR) Z3 e Z4
da transmissão a seguir. A transmissão será acionada por um motor de P=7,5CV
(≈5,5 kW) que atuará com uma rotação de 1140rpm. O material a ser utilizado é o
SAE 8640. A dureza especificada é 60 HRC com duração prevista para 10000h. As
engrenagens atuarão em eixos de transmissão com carga uniforme, com serviço
contínuo de 24h/dia. Considere:
b1/do1 = 0, 25
α = 20
Z1 = 25
Z2 = 51
Z3 = 27
Z4 = 99 33 / 34

Engrenagem Cilíndricas de Dentes Helicoidais
34 / 34

Aula 3 e 4.pdf

Mais conteúdo relacionado

Semelhante a Aula 3 e 4.pdf

Aula 3 e 4.pdf