Transferir como ODP, PPTX
Carregado porDiego Souza Silva
Algoritmo Genético para busca de máximo de função
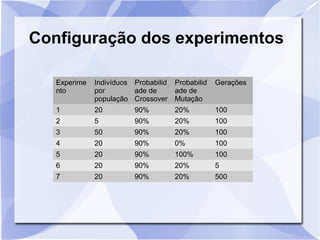
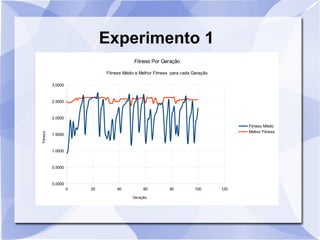
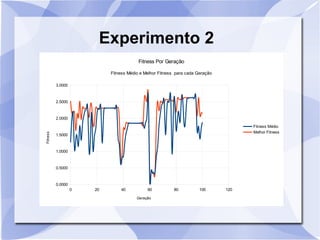
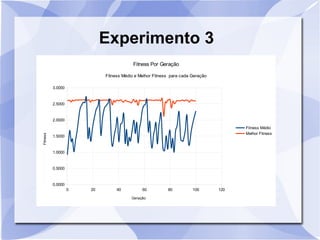
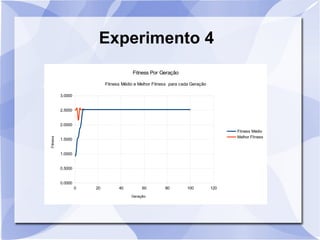
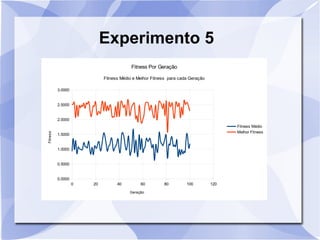
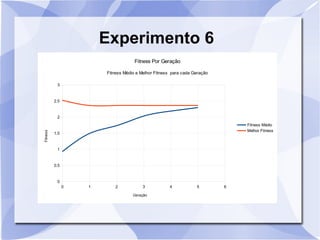
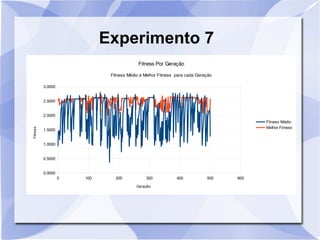
Este documento descreve um estudo que usa algoritmos genéticos para maximizar uma função matemática. Ele define algoritmos genéticos e descreve sete experimentos variando parâmetros como tamanho da população, probabilidade de crossover e mutação. Os resultados são analisados usando gráficos do fitness médio e melhor ao longo das gerações.
Algoritmo Genético para busca de máximo de função
- 1. Introdução a ComputaçãoNatural: Algoritmo Genético aplicado a maximização de funções Por Diego de Souza Silva RA 090911
- 2. Introdução Os algoritmos genéticos,assim como outros bioinspirados, são heurísticas utilizadas na busca de resolução em problemas complexos que ou não tem solução exata ou demanda mais tempo do que se é desejável para ser descoberta. Este trabalho consiste em utilizar um algoritmo genético clássico na maximização de uma função e analisar a qualidade das soluções encontradas por meio de gráficos gerados.
- 3. Roteiro ● Referencial Teórico, ●Materiais e Métodos, ● Resultados e Discussão, ● Bibliografia.
- 4. Referenciais Teóricos: Computaçãonatural Consiste em uma abordagem relativamente nova na resolução de problemas computacionais caracterizada por se basear em eventos da natureza. Podemos definir a computação natural como uma linha de pesquisa que permite o desenvolvimento de novas ferramentas de computação na resolução de problemas e se baseia em mecenismos naturais para o desenvolvimento de novos algoritmos.
- 5. Algoritmo Genético Algoritmos genéticosé uma classe dentre os algoritmos evolutivos (beseados na evolução biológica) que usam técnicas inspiradas pelos conceitos da teoria Darwinista da evolução como hereditariedade, mutação, seleção natural e recombinação (ou crossing over). São implementados como uma simulação de computador em que uma geração de indivíduos que representam soluções são escolhidos os mais aptos a se gerarem descendentes-soluções. A evolução geralmente se inicia a partir de um conjunto de soluções criado aleatoriamente e é realizada por meio de gerações. A cada nova geração, a adaptação de cada solução na população é avaliada, alguns indivíduos são selecionados para a próxima geração, e recombinados ou mutados para formar uma nova população. A população gerada então é utilizada como entrada para a próxima iteração do algoritmo.
- 6. O experimento O experimentoproposto neste trabalho consiste em desenvolver um algoritmo genético clássico, utilizá-lo na maximização da função f1: f1 = x * sin(4*pi*x) – y*sin(4*pi*y+pi)+1 com parâmetros diversos e gerando para cada versão dos parâmetros um gráfico com o fitness médio e melhor de cada geração.
- 7. Configuração dos experimentos Experime nto Indivíduos por população Probabilid adede Crossover Probabilid ade de Mutação Gerações 1 20 90% 20% 100 2 5 90% 20% 100 3 50 90% 20% 100 4 20 90% 0% 100 5 20 90% 100% 100 6 20 90% 20% 5 7 20 90% 20% 500
- 8. Experimento 1 0 2040 60 80 100 120 0.0000 0.5000 1.0000 1.5000 2.0000 2.5000 3.0000 Fitness Por Geração Fitness Médio e Melhor Fitness para cada Geração Fitness Médio Melhor Fitness Geração Fitness
- 9. Experimento 2 0 2040 60 80 100 120 0.0000 0.5000 1.0000 1.5000 2.0000 2.5000 3.0000 Fitness Por Geração Fitness Médio e Melhor Fitness para cada Geração Fitness Médio Melhor Fitness Geração Fitness
- 10. Experimento 3 0 2040 60 80 100 120 0.0000 0.5000 1.0000 1.5000 2.0000 2.5000 3.0000 Fitness Por Geração Fitness Médio e Melhor Fitness para cada Geração Fitness Médio Melhor Fitness Geração Fitness
- 11. Experimento 4 0 2040 60 80 100 120 0.0000 0.5000 1.0000 1.5000 2.0000 2.5000 3.0000 Fitness Por Geração Fitness Médio e Melhor Fitness para cada Geração Fitness Médio Melhor Fitness Geração Fitness
- 12. Experimento 5 0 2040 60 80 100 120 0.0000 0.5000 1.0000 1.5000 2.0000 2.5000 3.0000 Fitness Por Geração Fitness Médio e Melhor Fitness para cada Geração Fitness Médio Melhor Fitness Geração Fitness
- 13. Experimento 6 0 12 3 4 5 6 0 0.5 1 1.5 2 2.5 3 Fitness Por Geração Fitness Médio e Melhor Fitness para cada Geração Fitness Médio Melhor Fitness Geração Fitness
- 14. Experimento 7 0 100200 300 400 500 600 0.0000 0.5000 1.0000 1.5000 2.0000 2.5000 3.0000 Fitness Por Geração Fitness Médio e Melhor Fitness para cada Geração Fitness Médio Melhor Fitness Geração Fitness
- 15. Conclusão Embora possa ignorara melhor solução, o algoritmo oferece boas respostas para o problema de maximização desde que se use populações suficientemente numerosas e se equilibre a probabilidade de reprodução por crossover e por mutação.