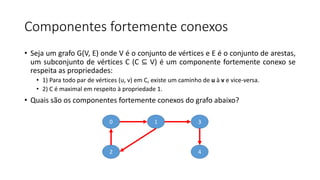
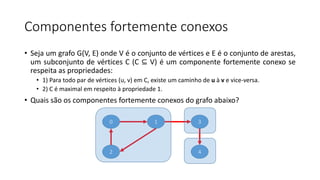
O documento descreve o algoritmo de Kosaraju para encontrar componentes fortemente conexos em um grafo. O algoritmo realiza uma DFS no grafo original e em seu transposto, empilhando os vértices visitados. Uma segunda DFS nos vértices empilhados encontra os componentes.

1. Algoritmo de Kosaraju
Marcos Castro

2. Componentes fortemente conexos
• Seja um grafo G(V, E) onde V é o conjunto de vértices e E é o conjunto de arestas,
um subconjunto de vértices C (C ⊆ V) é um componente fortemente conexo se
respeita as propriedades:
• 1) Para todo par de vértices (u, v) em C, existe um caminho de u à v e vice-versa.
• 2) C é maximal em respeito à propriedade 1.
• Quais são os componentes fortemente conexos do grafo abaixo?
0
2
1 3
4

3. Componentes fortemente conexos
• Seja um grafo G(V, E) onde V é o conjunto de vértices e E é o conjunto de arestas,
um subconjunto de vértices C (C ⊆ V) é um componente fortemente conexo se
respeita as propriedades:
• 1) Para todo par de vértices (u, v) em C, existe um caminho de u à v e vice-versa.
• 2) C é maximal em respeito à propriedade 1.
• Quais são os componentes fortemente conexos do grafo abaixo?
0
2
1 3
4

4. Componentes fortemente conexos
• Aplicação: em redes sociais, pode-se detectar grupos de pessoas fortemente
conectadas para sugerir algo como páginas, games, amizades.
• Como detectar todos os componentes fortemente conexos?
• Iremos utilizar o algoritmo de Kosaraju.
• A complexidade desse algoritmo é O(V + E) utilizando lista de adjacência.
• Primeiramente será explicado o algoritmo.
• Após a explicação, será disponibilizado um link com a implementação em C++.

5. Algoritmo
• Crie uma pilha vazia e faça uma DFS no grafo.
• Ao final de cada DFS, insira o vértice na pilha como mostra o algoritmo:
Inicialmente o vetor de visitados
é preenchido com falso.

6. Algoritmo
• Obtenha o grafo transposto
• Basta inverter as orientações das arestas do grafo original.
• Os vértices são os mesmos do grafo original, só inverte as arestas!

7. Algoritmo
• Marque novamente todos os vértices como não visitados para a segunda DFS.
• Enquanto a pilha não for vazia:
• Obtenha o elemento do topo.
• Remova o elemento do topo.
• Se esse elemento não foi visitado, realize uma DFS nele.

8. Algoritmo
• Algoritmo da função DFS:

9. Código
• A implementação foi feita em C++, segue o link:
• https://gist.github.com/marcoscastro/362854424c34bcec92cb

10. Contato
mcastrosouza@live.com
www.geeksbr.com
www.github.com/marcoscastro
www.youtube.com/c/marcoscastrosouza