10. Sistemas e Controles Eletrônicos

UNIVERSIDADE FEDERAL DE SERGIPE
CENTRO DE CIÊNCIAS EXATAS E TECNOLOGIA
NÚCLEO DE ENGENHARIA MECÂNICA

Sistemas e Controles Eletrônicos

11/08/2009 18:21 Prof. Douglas Bressan Riffel 1

NÚCLEO DE ENGENHARIA MECÂNICA Conteúdo

• Introdução
d ã
– Motivação
– Conceitos Básicos
• Aplicação dos Sistemas de Controle
– Regulador de Esferas (James Watt - 1769)
– Aplicações Espaciais
– Robótica
– Má i
Máquinas Elét i
Elétricas


NÚCLEO DE ENGENHARIA MECÂNICA Introdução
ç

• Motivação:
i ã
– Manipulação de processos (controle de
temperatura, controle de velocidade, etc.).
– Automação de tarefas repetitivas.
– Obtenção de um resultado satisfatório.
• Presente no Cotidiano
– Caixa eletrônico
– Aviões (piloto automático)
– Automóveis (controle de tração.)
Controle é o mecanismo utilizado para manter o equilíbrio.

UNIVERSIDADE FEDERAL DE SERGIPE Sistemas de Controle
NÚCLEO DE ENGENHARIA MECÂNICA Visão geral
g

Sensores melhores
mais visão.

Melhores atuadores
M lh t d
mais músculos.

Melhor controle
maior precisão, combinando sensores e atuadores
p ,
de uma forma mais “inteligente”.



• Conceitos Básicos (Exemplo)

Objetivo: Independente das variações na temperatura ambiente,
a temperatura interna do forno deve ser constante.



• Conceitos Básicos
– SISO (Single Input Single Output)

Entrada Saída
Planta
(Processo)

– MIMO (Multiple Input Multiple Output)



• Introdução
d ã
– Motivação
– Conceitos Básicos
• Aplicação dos Sistemas de Controle
– 300 a.C. – Grécia: relógio de água (Ktesibios)
– Regulador de Esferas (James Watt - 1769)
– Aplicações Espaciais
– R bóti
Robótica
– Máquinas Elétricas


UNIVERSIDADE FEDERAL DE SERGIPE ROTAÇÃO
NORMAL

Regulador de Esferas
James Watt - 1769
J W tt

FLUXO DE VAPOR NORMAL

ROTAÇÃO
ALTA

11/08/2009de algodão – Manchester - Douglas Bressan Riffel
Fábrica 18:21 Prof. UK FLUXO DE VAPOR RESTRINGIDO
8

NÚCLEO DE ENGENHARIA MECÂNICA Aplicações Espaciais
p ç p

Antena para Rastreio de Satélites
INPE/UFRN

• Motores
• Drivers
• Engrenagens
• Redutores
Lançamento do foguete VSB-30
• Sensores Alcântara - 19/07/2007 - INPE

Robótica
NÚCLEO DE ENGENHARIA MECÂNICA Miguel Nicolelis – Indicado ao
g
Nobel de Medicina

Japão EUA


NÚCLEO DE ENGENHARIA MECÂNICA Máquinas Elétricas
q

Instalação do primeiro gerador na década de 80
1760 toneladas, 16 m de diâmetro, 700 MW


• Classificação d Sistemas d Controle
l ifi ã dos i de l
– Controle em Malha Aberta
– Controle em Malha Fechada
– Malha Aberta x Malha Fechada
• Vantagens e Desvantagens
• Conclusões e Considerações Finais


UNIVERSIDADE FEDERAL DE SERGIPE Classificação dos Sistemas de
NÚCLEO DE ENGENHARIA MECÂNICA Controle

• Controle em Malha Aberta
– Características:
• Sinal de controle predeterminado.
– Exemplos:
• Automóvel sem velocímetro.
– Experiência do Motorista
Motorista.
– Carga do veículo, terreno e rajadas de vento.
• Lava-roupas.
p
– Escolhe-se o “programa de lavagem”.


UNIVERSIDADE FEDERAL DE SERGIPE Classificação dos Sistemas de
NÚCLEO DE ENGENHARIA MECÂNICA Controle

• Controle em Malha Fechada
– Características
• Medição do sinal de saída.
• Sinal de controle em função da saída.
– Exemplos:
• Automóvel com velocímetro
velocímetro.
• Forno com sensor de temperatura.



Classificação dos Sistemas de Controle
• Diagrama de blocos

• Para o exemplo do carro:
– Sensor: Olhos do motorista
– Controlador: Cérebro do motorista.
– Atuador: Motor do automóvel.


NÚCLEO DE ENGENHARIA MECÂNICA Malha Aberta x Malha Fechada

• Controle em Malha Aberta
– Vantagens:
g
• Barato (não precisa de sensores).
• Conveniente quando não se pode medir a saída.
• Construção simples e manutenção fácil.
– Desvantagens:
• Sensível a perturbações.
• Impreciso
Impreciso.


NÚCLEO DE ENGENHARIA MECÂNICA Malha Aberta x Malha Fechada

• Controle em Malha Fechada
– Vantagens:
g
• Boa precisão quando comparado ao sistema em malha
aberta.
• Rejeita o efeito das perturbações sobre a variável do
processo.
– Desvantagens:
• Mais complexo e caro (
p (uso de sensores).
)


UNIVERSIDADE FEDERAL DE SERGIPE Modelagem no Domínio da
NÚCLEO DE ENGENHARIA MECÂNICA Freqüência

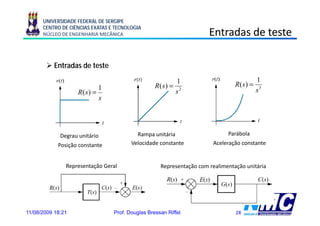
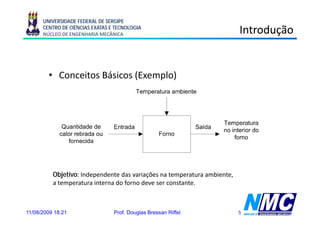
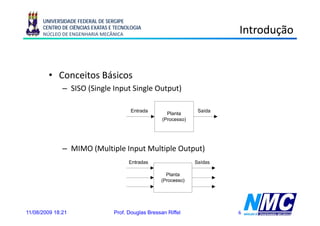
Objetivo: Função de Transferência
Entrada Saída
Sistema

Entrada Saída
Subsistema Subsistema Subsistema

Revisão sobre Transformada de Laplace
• A transformada de Laplace é definida como:
∞
L[ f (t )] = F ( s ) = ∫ f (t )e − st dt
0−

em que: s = σ + jω é uma variável complexa.
• O limite inferior da integral significa que, mesmo se f(t) for descontínua em
t=0, pode-se começar a integração antes da referida, desde que a integral
convirja.
j


UNIVERSIDADE FEDERAL DE SERGIPE Modelagem no
NÚCLEO DE ENGENHARIA MECÂNICA Domínio da Freqüência

• A transformada inversa de Laplace é dada por:
1 σ + j∞
2πj ∫σ − j∞
−1
L [ F ( s )] = f (t )u (t ) = F ( s )e st ds

onde u(t) = 1, p/ t > 0 ou u(t) = 0, p/ t < 0. (função degrau unitário)
Algumas f õ representativas
Al funções t ti

f (t ) F (s ) f (t ) F (s )
δ (t ) 1
1 e − at u (t )
1 s+a
u (t ) ω
s sin ωtu (t )
s2 + ω 2
t n u (t ) n!
s
s n +1 cos ωtu (t )
s2 + ω 2


NÚCLEO DE ENGENHARIA MECÂNICA Domínio da Freqüência

Função de Transferência
F ã d T f ê i
Escrevendo a saída C(s) em função de R(s), obtém-se:
C ( s) (bm s m + bm −1s m −1 + ... + b0 )
= G (s) =
R( s) (an s n + an −1s n −1 + ... + a0 )
A relação de polinômios acima G(s), denomina-se de Função de
Transferência e o seu cálculo é feito com condições iniciais nulas.

Problema:
Obter a função de transferência representada por:
dc(t )
+ 2c(t ) = r (t )
dt
Solução: Aplicando Laplace,
C ( s) 1
sC ( s ) + 2C ( s ) = R( s) ⇒ G ( s) = =
R( s) s + 2


NÚCLEO DE ENGENHARIA MECÂNICA Domínio do Tempo

Objetivo: Representação em espaço de estados
• Considere o circuito RL abaixo, com condições iniciais nulas:
Para a corrente i(t), pode-se escrever:
di
d
v(t ) = L + Ri
dt
Por Laplace,
V ( s ) = L[ sI ( s ) − i (0)] + RI ( s )
Se V(s) for um degrau unitário,
1 ⎛1 1 ⎞ i (0)
I (s) = ⎜ − ⎟ +
L⎝ s s+R/L⎠ s+R/L
Aplicando a transformada inversa de Laplace
Laplace,

i (t ) =
1
L
(1 − e−( R / L)t ) + i(0)e−( R / L)t onde i(t) é uma variável de estado.



A variável de estado i(t) é obtida a partir da equação de estado
di
L + Ri = v(t )
(
dt
A partir de i(t) e de v(t), pode-se obter outras variáveis de circuito:
vR (t ) = Ri (t ) tensão sobre o resistor.
vL (t ) = v(t ) − Ri (t ) tensão sobre o indutor.
di 1
= [v(t ) − Ri ] derivada da corrente.
dt L
Determinando-se a variável de estado i(t) e a entrada v(t), pode-se obter o
estado de qualquer variável de circuito para t >= to
to.
As equações acima são denominadas de equações de saída.
O sistema de equações que combina equações de estado e de saída compõe a
representação no espaço de estado do sistema
sistema.



A equação de estado que representa o circuito exemplo não é única.
Por exemplo: considere i = vR/R, então:
L dvR
+ vR = v(t )
R dt
Considere agora um sistema de segunda
ordem:
di 1
L + Ri + ∫ idt = v(t )
dt C
fazendo i(t) = dq/dt,
d 2q dq 1
L 2 +R + q = v(t )
dt dt C
Uma equação de ordem n pode ser convertida em n equações de primeira
ordem.
ordem



As equações de primeira ordem resultantes são do tipo:
dxi
= ai1 x1 + ai 2 x2 + ... + aiin xn + bi f (t )
dt
onde cada xi é uma variável de estado, e os coeficientes aij e bi são constantes
nos sistemas lineares e invariantes no tempo, sendo f(t) a entrada.

Assim, podemos resolver a equação do circuito em termos de q(t) e i(t).
Como dq/dt = i, então o seguinte sistema pode ser escrito:
dq
=i
dt
di 1 ⎡ 1 ⎤
= ⎢− q − Ri + v( )⎥
(t
dt L ⎣ C ⎦
O sistema de equações acima, associado a uma equação de saída,
corresponde a representação no espaço de estado sistema.



Um exemplo de equação de saída é:
1
vL (t ) = − q (t ) − Ri (t ) + v(t )
C
• Observe que a equação de saída é uma combinação linear das variáveis de
estado.
Outras variáveis de estado podem também ser escritas, por exemplo:
dvR 1
= [− RvR − RvC + Rv(t )]
dt L
dvC 1
= vR
dt RC
As variáveis de estado devem ser linearmente independentes.
Do ponto de vista de aplicabilidade, as equações de estados devem ser
lineares.



As equações de estado podem ser representada matricialmente:
x = Ax + Bu
&
onde:
⎡dq / dt ⎤ ⎡ 0 1 ⎤ ⎡q ⎤ ⎡ 0 ⎤
& =⎢ A=⎢ ⎥ x = ⎢ i ⎥ B = ⎢1 / L ⎥ u = v(t )
di / dt ⎥
x
⎣ ⎦ ⎣− 1 / LC − R / L⎦ ⎣ ⎦ ⎣ ⎦
A equação de saída para y(t) = vL(t) é dada por
y = Cx + Du
onde:
C = [− 1 / C − R] D =1
• D fi i õ
Definições:
1. Combinação linear: Uma combinação linear de n variáveis é definida como:

S = k n xn + k n −1 xn −1 + ... + k1 x1



Representação em espaço de estados
• Definições:
2. Variáveis de sistema: Qualquer variável que responda a uma entrada ou a condições
iniciais
i i i i em um sistema.
it
3. Variáveis de estado: Menor conjunto linearmente independente de variáveis de sistema
que determinam os valores das variáveis de sistema para t >= to.
4. Vetor de estado: Vetor cujos elementos são variáveis de estado.
5. Espaço de estado: Espaço n-dimensional cujos eixos são variáveis de estado.
6.
6 Equações de estado: Conjunto de n equações diferenciais de primeira ordem
ordem.
7. Equações de saída: Equações algébricas que representam as variáveis de saída de um
sistema como combinações lineares das variáveis de estado e da entrada.

x = Ax + Bu
&
y = Cx + Du


NÚCLEO DE ENGENHARIA MECÂNICA Entradas de teste

Entradas de teste

1 1
1 R(s ) =
(s R(s ) =
(
R( s) = s2 s3
s

Degrau unitário
g Rampa unitária Parábola
Posição constante Velocidade constante Aceleração constante

Representação Geral
R ã G l Representação com realimentação unitária
R ã li ã iái


Resposta ao degrau
NÚCLEO DE ENGENHARIA MECÂNICA no Domínio do Tempo
p

Sistemas de Segunda Ordem – Tipos de respostas


Resposta ao degrau
p

Sistemas de Segunda Ordem – Tipos de respostas


Resposta ao degrau
p

Sistemas Subamortecido – Especificações
Cálculo de Tp
Ou seja:
ωn
ωn 1 − ξ 2
1− ξ 2
=
( s + ξωn ) 2 + ωn (1 − ξ 2 )
ξ 2

Portanto:

c(t ) =
&
ωn
1− ξ 2
(
e −ξωnt sin ωn 1 − ξ 2 t )
Igualando a zero,
nπ
t = Tp =
ωn 1 − ξ 2


Resposta ao degrau
p

Sistemas Subamortecido – Análise Gráfica
Respostas ao degrau em função da movimentação dos pólos
1. Parte real constante:


Resposta ao degrau
p

2. Parte imaginária constante:


Resposta ao degrau
p

3. Com relação de amortecimento constante:


Resposta ao degrau
p

Sistemas Subamortecido – Pólos Adicionais
Resposta do sistema com a adição de um pólo ao sistema subamortecido.


Resposta ao degrau
p

Sistemas Subamortecido – Zeros

A inclusão de um zero na planta de
controle altera basicamente a
amplitude da ultrapassagem
(overshoot)


NÚCLEO DE ENGENHARIA MECÂNICA Erros de Estado Estacionário

• Admita o sistema de controle :

• O erro entre a entrada e a saída é dado por:
E ( s) = R( s) − C ( s) mas como C ( s ) = E ( s )G ( s )
R( s)
então, E (s) =
1 + G (s)
• Fazendo t ir para ∞, obtém-se que:
sR(s)
(s
e(∞) = lim
s →0 1 + G ( s )



Constantes de erros estáticos e tipo de sistema
• Constante de Posição Kp

s(1 / s ) 1
e(∞ ) = edeg rau ( ∞ ) = lim =
s →0 1 + G ( s ) 1 + lim G ( s )
s →0

K p = lim G ( s ) 1
s →0
edeg rau ( ∞ ) =
1+ Kp
• Constante de Velocidade Kv

K v = lim sG ( s ) 1
s →0
erampa (∞ ) =
p
Kv
• Constante de Aceleração Ka

1
K a = lim s 2G ( s ) e parábola ( ∞ ) =
s →0 Ka


Tipos de sistema
Ti d it

Degrau Rampa Aceleração
r(t) = 1 r(t) = t r(t) = t² /2
Tipo 0 1
∞ ∞
1+ K
Tipo 1
0 1 ∞
K
Tipo 2
1
0 0 K

C( s) ( s − z1 )( s − z2 )( s − zn ) K (T s + 1)(Tb s + 1)...
= G( s) = ? = ? a
R( s ) s ( s − p1 )( s − p2 )( s − pm ) s (T1s + 1)(T2 s + 1)...

UNIVERSIDADE FEDERAL DE SERGIPE Controladores Eletrônicos
NÚCLEO DE ENGENHARIA MECÂNICA Proporcional - P

R2
R4
R1
R3

+
+

R4 R2
G( s) =
R3 R1


NÚCLEO DE ENGENHARIA MECÂNICA Integral - I

C2
R4
R1
R3

+
+

R4 1
G( s) =
R3 R1C2 s


NÚCLEO DE ENGENHARIA MECÂNICA Proporcional-
Proporcional-Derivativo - PD

C1 R2
R4
R1
R3

+
+

R4 R2
G( s) = (R1C1s + 1)
R3 R1


NÚCLEO DE ENGENHARIA MECÂNICA Proporcional-
Proporcional-Integral - PI

R2 C2
R4
R1
R3

+
+

R4 R2 R2C2 s + 1
G( s) =
R3 R1 R2C2 s


NÚCLEO DE ENGENHARIA MECÂNICA Proporcional-Integral-Derivativo
Proporcional-Integral- e at o
opo c o a teg a
PID
C1 R2 C2
R4
R1
R3

+
+

R4 R2 (R1C1s + 1)(R2C2 s + 1)
G( s) =
R3 R1 R2C2 s


Exemplo de Utilização
NÚCLEO DE ENGENHARIA MECÂNICA Compensador


10. Sistemas e Controles Eletrônicos

Mais conteúdo relacionado

Semelhante a 10. Sistemas e Controles Eletrônicos

Mais de UFS - Brasil / Prof. Douglas Bressan Riffel

10. Sistemas e Controles Eletrônicos