Exercícios de análise de investimentos e mercado de capitais

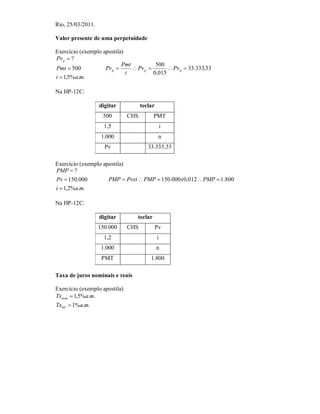
1. Rio, 25/03/2011.
Valor presente de uma perpetuidade
Exercício (exemplo apostila)
Pv p  ?
Pmt 500
Pmt  500 Pv p   Pv p   Pv p  33.333,33
i 0,015
i  1,5% a.m.
Na HP-12C:
digitar teclar
500 CHS PMT
1,5 i
1.000 n
Pv 33.333,33
Exercício (exemplo apostila)
PMP  ?
Pv  150.000 PMP  Pvxi  PMP  150.000 x0,012  PMP  1.800
i  1,2%a.m.
Na HP-12C:
digitar teclar
150.000 CHS Pv
1,2 i
1.000 n
PMT 1.800
Taxa de juros nominais e reais
Exercício (exemplo apostila)
Txnom  1,5%a.m.
Txinf  1% a.m.

2. Expressão completa:
  1,5   
   1
 Tx     100      0,015  1  
Txreal   nom   1 x100  Txreal
      1 x100  Txreal     1 x100
 Txinf     1   1  
   0,01  1  
  100   
  
 1,015  
Txreal     1 x100  Txreal  (1,00495049  1) x100  Txreal  0,00495049x100
 1,01  
Txreal  0,495%a.m.
Obs.: Relembrando que uma regra da matemática diz que devemos resolver as contas
respeitando a ordem a seguir:
1- Parênteses;  (x)
2- Colchetes  [x]
3- Chaves  {x}
Se estiver muito complicado, podemos fazer assim:
Txnom  1,5%a.m.  (1,5 / 100)  1  0,015  1  1,015
Txinf  1% a.m.  (1 / 100)  1  0,01  1  1,01
Pegamos os resultados, e aplicamos na fórmula:
Txnom 1,015
Txreal   Txreal   Txreal  1,00495049
Txinf 1,01
Ainda não chegamos ao resultado final. Diminuímos o resultado de 1 e multiplicamos
por 100:
Txreal  1,00495049  1x100  Txreal  0,00495049x100  Txreal  0,495%a.m.
Na HP-12C:
digitar teclar
1,5 enter
100 
1 +
1 Enter
100 
1 +
 1,00495049
1 -
100 x
0,4950

3. 19)
1º caso:
Txnom  18%
Txinf  12%
  18   
   1 
Txnom   100     0,18  1  
Txreal   Txreal     1 x100  Txreal     1 x100
Txinf   12   1 
   0,12  1  
  100   
  
 1,18  
Txreal     1 x100  Txreal  (1,053571  1) x100  Txreal  0,053571x100
 1,12  
Txreal  5,357%
2º caso:
Txnom  42%
Txinf  8%
  42   
   1
Txnom   100      0,42  1  
Txreal   Txreal     1 x100  Txreal     1 x100
Txinf    8   1 
   0,08  1  
  100   
  
 1,42  
Txreal     1 x100  Txreal  (1,314814  1) x100  Txreal  0,314814x100
 1,08  
Txreal  31,481%
3º caso:
Txnom  12%
Txinf  16%
  12   
   1 
Txnom   100     0,12  1  
Txreal   Txreal     1 x100  Txreal     1 x100
Txinf   16   1 
    0,16  1  

  100    
 1,12  
Txreal     1 x100  Txreal  (0,965517  1) x100  Txreal  0,034483x100
 1,16  
Txreal  3,448% 
parênteses indicando valor negativo
4º caso:
Txnom  9,5%
Txinf  12,3%

4.   9,5   
   1 
Txnom  100     0,095  1  
Txreal   Txreal      1 x100  Txreal     1 x100
Txinf   12,3   1  
    0,123  1  
  100   
  
 1,095  
Txreal     1 x100  Txreal  (0,975066  1) x100  Txreal  0,024934x100
 1,123  
Txreal  2,493% 
Taxa média de retorno
TMR= Lucro contábil anual médio
Metade do investimento inicial
Exercício (exemplo apostila)
0 1 2 3 4
(40.000) 8.000 16.000 18.000 22.000
Para obtermos o lucro líquido médio devemos somar todos as receitas nos períodos de
tempo e dividirmos pela quantidade de períodos:
8.000  16.000  18.000  22.000
Lucro líquido médio=  16.000
4
Para descobrirmos o investimento médio basta dividir o investimento inicial por 2:
40.000
Investimento médio=  20.000
2
Agora descobrimos a Taxa média de retorno:
16.000
TMR   TMR  0,8  x100  80%
20.000
Exercício 25
Pererecas:
3.000  5.000  6.000  9.000  12.000
Lucro líquido médio=  7.000
5
25.000
Investimento médio=  12.500
2
7.000
TMR   TMR  0,56  x100  56%
12.500

5. Minhocas:
2.000  6.000  6.000  8.000  8.000
Lucro líquido médio=  6.000
5
18.000
Investimento médio=  9.000
2
6.000
TMR   TMR  0,667  x100  66,7%
9.000
Aceitar o projeto das minhocas pois este apresenta retorno superior ao das pererecas
(66,7% contra 56%).
Taxa média de retorno
Exercício (exemplo apostila) Aqui a gente recebe as
Aqui a gente gasta o receitas nos anos seguintes
dinheiro para iniciar o ao início do negócio.
negócio.
ano investimento lucro Saldo a recuperar
0 (10.000) (10.000)
1 2.000 (8.000)
2 2.000 (6.000)
3 4.000 (2.000)
4 4.000 2.000
5 5.000 7.000
Aqui o saldo a recuperar
diminui à medida que
recebemos as receitas (lucros).
 2.000  2.000
PB  3     PB  3,5anos  0,5  x12  6meses , então:
 4.000  4.000
PB=3anos e 6meses, pois 0,5 ano é igual a ½ ano que corresponde a 6meses.
Não aceitar o projeto, pois o payback é maior que o determinado pelo investidor
(3anos).
Exercício 25
Projeto 1 Projeto 2
saldo a saldo a
ano investimento lucro hist. investimento lucro hist.
recuperar recuperar
0 (70.000) (70.000) (70.000) (70.000)
1 20.000 (50.000) 5.000 (65.000)
2 40.000 (10.000) 30.000 (35.000)
3 30.000 20.000 30.000 (5.000)
4 20.000 40.000 30.000 25.000
5 15.000 55.000 50.000 75.000

6. Projeto1:
 10.000  10.000
PB  2     PB  2,33anos  0,333  x12  4meses , então:
 30.000  30.000
PB=2anos e 4meses, pois 0,333 ano é igual a 1/3 ano que corresponde a 4meses.
Projeto2:
 5.000  5.000
PB  3     PB  3,16anos  0,16  x12  2meses , então:
 30.000  30.000
PB=3anos e 2meses, pois 0,16 ano é igual a 1/6 ano que corresponde a 2meses.
Aceitar o projeto 1 pois este tem um tempo de retorno menor que o projeto 2, ou seja,
no projeto 1 teremos de volta o dinheiro que aplicamos em 2anos e 4meses e no projeto
2 em 3anos e 2meses.