Este relatório científico descreve um projeto que tem como objetivo aplicar o Método dos Elementos Finitos (MEF) para resolver problemas do eletromagnetismo, como a análise modal de guias ópticos planares. O trabalho envolve desenvolver programas MEF unidimensionais e bidimensionais, adaptá-los para execução em sistemas de computação distribuída, e realizar estudos comparativos de desempenho. Os programas desenvolvidos terão capacidade de refinar automaticamente a malha de elementos finitos.

1. BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
,QLFLDomR &LHQWtILFD ,
BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB
Relatório Científico
Bolsa – Processo Fapesp No
: 02/12344-01
IDENTIFICAÇÃO DO RELATÓRIO
PROJETO: Aplicação do Método dos Elementos Finitos a
Problemas do Eletromagnetismo em Sistema de Computação
de Alto Desempenho
Bolsista: Marco Antonio Hidalgo Cunha
Orientador: Dr. Marcos Antônio Ruggieri Franco
Período: Fev./2003 a Julho/2003
Instituição:
Instituto de Estudos Avançados do Centro
Técnico Aeroespacial – IEAv - CTA
Número do Relatório 01

2. 2
6XPiULR
, 2EMHWLYR
,, 5HVXPR GR 3URMHWR
,,, 0pWRGR GRV (OHPHQWRV )LQLWRV
A. Introdução..........................................................................................................4
B. Como é aplicado o Método dos Elementos Finitos...........................................4
C. Esquema Simplificado de um Programa de Elementos Finitos ........................5
D. Método Clássico para a Solução de Problemas de Valor de Contorno.............5
1. Método de Galerkin ............................................................................5
E. Função de Base para Elemento Finito 1D.........................................................7
,9 $QiOLVH 0RGDO GH *XLDV ÏSWLFRV 3ODQDUHV
9 $ERUGDJHP $QDOtWLFD SDUD (VWXGR GH *XLDV ÏSWLFRV 3ODQDUHV
A. Programa para cálculo analítico dos autovalores ( ¡ ¡
Q ) em guias ópticos
planares simétricos e isotrópicos.....................................................................11
9, $ERUGDJHP 1XPpULFD )RUPXODomR GR 0() SDUD (VWXGR GH *XLDV ÏSWLFRV
3ODQDUHV $QLVRWUySLFRV H 1mR+RPRJrQHRV
A. Exemplo de Aplicação.....................................................................................17
1. Caso de Estudo: Guia Planar Homogêneo, Isotrópico e Simétrico ..17
9,, $QiOLVH 1XPpULFD GH *XLDV ÏSWLFRV 3ODQDUHV $QLVRWUySLFRV H 1mR+RPRJrQHRV
A. Guia Planar Formado por Processo de Difusão (Ti:LiNbO3)..........................19
B. Caso de Estudo: Guia Óptico Planar Não-Homogêneo, Anisotrópico e
Não-Simétrico (guia tipo Ti:LiNbO3) ............................................................20
9,,, 3URJUDPD SDUD $QiOLVH 0RGDO GH *XLDV ÏSWLFRV 3ODQDUHV H 'HVFULomR GD
,QWHUIDFH *UiILFD SDUD (QWUDGD GH 'DGRV H 9LVXDOL]DomR *UiILFD GH 5HVXOWDGRV
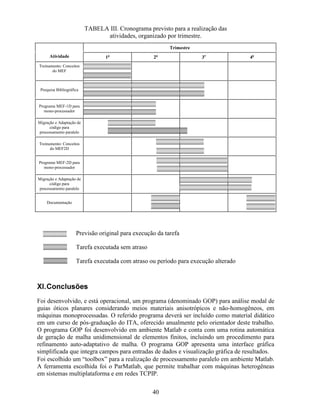
A. Fluxograma do Programa GOP .......................................................................22
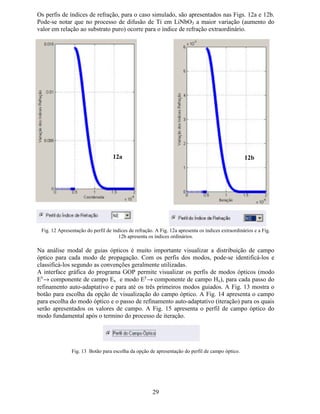
B. Descrição da Interface Gráfica do programa GOP..........................................23
1. Parâmetros de Entrada ......................................................................24
2. Opções para Visualização Gráfica de Resultados.............................26
3. Visualização de Resultados...............................................................28
4. Informações Sobre o Processo Difusivo...........................................34
5. Informações Sobre o Programa GOP................................................34
6. Informações Sobre o Projeto.............................................................35
,; 0LJUDomR H $GDSWDomR GH 3URJUDPD GH 0()' SDUD 6LVWHPD GH 3URFHVVDPHQWR
'LVWULEXtGR
A. Abordagem Primeira: Utilização do Programa Octave-MPI com Sistema
Operacional Linux...........................................................................................36
1. Requisitos para utilização do Octave-MPI .......................................36
2. Problemas encontrados para compilar o Octave-MPI ......................36
B. Abordagem Segunda: Utilização do Programa Matlab em Sistema de
Computação Distribuída Baseado em Sistemas Mistos (Windows e Linux)..36
1. Pesquisa sobre pacotes disponíveis para utilização do Matlab em
computação distribuída.....................................................................36
2. O Toolbox ParMatlab ......................................................................38
3. Adaptação do programa GOP-simplificado para sistema de
computação distribuída.....................................................................38
; 3HUVSHFWLYDV
;, RQFOXV}HV
;,, 5HIHUrQFLDV %LEOLRJUiILFDV

3. 3
, 2EMHWLYR
Desenvolvimento, teste e validação de programas de aplicação do Método dos Elementos
Finitos (MEF) a problemas do eletromagnetismo. Tais desenvolvimentos e testes, visam a
utilização do sistema de processamento distribuído para computação de alto desempenho,
denominado projeto “BELIEVe”.
,, 5HVXPR GR 3URMHWR
O trabalho, em desenvolvimento, pretende estabelecer procedimentos para a paralelização de
programas de aplicação do Método dos Elementos Finitos desenvolvidos em ambiente
Matlab.
Numa primeira fase de desenvolvimento, serão realizados estudos sobre o Método dos
Elementos Finitos, em abordagem unidimensional para a análise modal de guias ópticos
planares
Na segunda etapa, os programas desenvolvidos serão adaptados para execução em pacotes de
processamento numérico que permitam execução em sistemas operacionais Windows e Linux.
A seguir, serão realizadas a migração, adaptação e teste dos programas para processamento
paralelo.
Após estas etapas, serão iniciados os estudos relacionados à aplicação do Método dos
Elementos Finitos a problemas bi-dimensionais (2D) de fibras ópticas. De forma análoga, os
programas serão escritos e testados em máquinas monoprocessadas e posteriormente em
processamento paralelo.
Das atividades decorrentes deste trabalho, podem ser destacados os seguintes passos gerais:
1. Desenvolvimento de programa para aplicação do Método dos Elementos Finitos 1D para a
análise modal de guias ópticos planares com anisotropia (versão mono-processada).
2. Desenvolvimento de programa para aplicação do Método dos Elementos Finitos 2D para a
análise modal de guias fibras ópticas (versão mono-processada).
3. Adaptação dos programas desenvolvidos, em etapas anteriores, ao sistema de computação
distribuída – BELIEVe.
4. Análise comparativa de desempenho entre sistema mono-processado e de computação
distribuída.
Os programas desenvolvidos para problemas unidimensionais de propagação de ondas ópticas
terão a capacidade de construir automaticamente a malha de elementos finitos com um
algoritmo de refinamento auto-adaptativo.
Para problemas bi-dimensionais, os programas de análise modal deverão permitir a leitura de
dados de definição de geometria, malha de elementos finitos e propriedades físicas dos
materiais, segundo o padrão adotado no sistema de software para guias ópticos integrados, em
desenvolvimento por uma das equipes de pesquisadores do LEV (Laboratório de Engenharia
Virtual do IEAv) com apoio FAPESP (Proc. 98/07789-7) [1]-[2]. A análise de resultados, tal
como a visualização da distribuição dos campos ópticos, será realizada com o auxílio do
referido sistema de software.

4. 4
,,, 0pWRGR GRV (OHPHQWRV )LQLWRV
$ ,QWURGXomR
O Método dos Elementos Finitos (MEF) tem se consagrado, nestas últimas duas décadas,
como uma das mais poderosas ferramentas utilizadas na análise e projeto de dispositivos
eletromagnéticos e sistemas elétricos.
Motivados pela diminuição do custo das estações de trabalho e dos microcomputadores e o
crescente aumento da capacidade de processamento e armazenamento, muitas universidades e
indústrias têm utilizado softwares com tecnologia CAD/CAE baseados no MEF. Esta
abordagem reduz o tempo necessário para as etapas de projeto e análise de desempenho,
diminuindo o número de protótipos necessários.
Apesar das equações de Maxwell descreverem completamente os fenômenos
eletromagnéticos macroscópicos, sua solução analítica é impraticável em dispositivos com
geometrias complexas. Os métodos numéricos são uma alternativa para a obtenção de
soluções aproximadas.
O MEF destaca-se pela capacidade de tratar problemas com geometria complexa, meios
materiais com anisotropia e não homogeneidades arbitrárias. O MEF permite incluir perdas e
ganhos e considerar meios lineares ou não lineares.
% RPR p DSOLFDGR R 0pWRGR GRV (OHPHQWRV )LQLWRV
Para utilizar o MEF, o modelo que representa o objeto de estudo deve ter sua geometria
subdividida em pequenas partes, que são os elementos finitos. Essa subdivisão é chamada
malha. No caso 1D a malha é constituída de segmentos de reta. No caso 2D a malha pode ser
constituída de triângulos, quadriláteros ou outras formas geométricas, cujos vértices são
denominados nós da malha. É através dela que se monta um sistema de equações cuja solução
permite determinar as grandezas de interesse no fenômeno utilizado.
As tarefas para a utilização do MEF podem ser divididas em três etapas, chamadas pré-
processamento, processamento e pós-processamento.
O SUpSURFHVVDPHQWR engloba o desenho da geometria do objeto (modelo geométrico), a
geração da malha (subdivisão do domínio), a imposição das propriedades físicas dos materiais
que constituem o objeto, a imposição dos valores das fontes de campo no objeto (densidade
de corrente elétrica em bobinas ou densidade de carga elétrica nos materiais...) e a imposição
das condições de contorno pertinentes ao fenômeno em análise.
O SURFHVVDPHQWR inclui a montagem do sistema de equações, através dos dados do pré-
processamento, e a sua resolução pode ser efetuada através de métodos diretos ou iterativos.
O SyVSURFHVVDPHQWR, com os dados das etapas anteriores, permite a utilização dos
resultados do MEF, através dos vários procedimentos de cálculo e formas de visualização das
grandezas do fenômeno estudado. Dentre as várias possibilidades de análise dos dados estão o
traçado de linhas de campo ou equipotenciais, cálculo da energia armazenada, força, torque,
capacitância, impedância, sobreposição de campos, etc.

5. 5
(VTXHPD 6LPSOLILFDGR GH XP 3URJUDPD GH (OHPHQWRV )LQLWRV
Modelo Geométrico (1D, 2D ou 3D)
Malha de elementos finitos
Propriedades Físicas e Condições de Contorno
Solução do Sistema de Equações
Exploração de Resultados
' 0pWRGR OiVVLFR SDUD D 6ROXomR GH 3UREOHPDV GH 9DORU GH
RQWRUQR
A seguir, revisaremos os aspectos gerais de um dos métodos clássicos para a solução de
problemas de valor de contorno o método de Galerkin que juntamente com o método de Ritz
contém a base do método dos elementos finitos [3].
Problemas de valor de contorno são muito empregados no modelamento de sistemas físicos.
Tipicamente pode ser definido por uma equação diferencial em um domínio Ω:
/φ I
Juntamente com as condições de contorno sobre a fronteira Γ que delimita o domínio. / é um
operador diferencial, I é a excitação e φ é a variável desconhecida.
A solução analítica dos problemas de valores de contorno limita-se a poucos casos especiais,
propagação de ondas em guias retangulares, circulares e elípticos, cavidades circulares e
esféricas e espalhamento de ondas por placas infinitas, cilindros e esferas. Muitos outros
problemas de interesse prático não têm solução analítica e os métodos de Ritz e Galerkin têm
sido largamente utilizados para superar essas dificuldades.
0pWRGR GH *DOHUNLQ
O método de Galerkin pertence à família dos métodos de resíduos ponderados, o qual como o
nome indica, aproxima a solução pela ponderação do resíduo da equação diferencial.
Considere a equação diferencial /φ I . Assuma que φ
~
é uma solução aproximada. A
substituição de φ por φ
~
na equação diferencial resulta um resíduo não nulo,
0
~
≠−= I/ φU .
A melhor aproximação para φ
~
será aquela que minimizar o valor de U em todos os pontos de
Ω. O método dos resíduos ponderados força esta condição

6. 6
0=Ω=
∫Ω
GU5 ω ,
onde 5¡ representa a integral do resíduo ponderado e ¢ω é a função de ponderação escolhida.
No método de Galerkin, a função peso é selecionada como sendo ser a mesma que a utilizada
na expansão da solução aproximada (φ
~
). Isto usualmente resulta uma solução mais acurada e
por isso esta técnica é tão popular.
Para ilustrar o método vamos assumir que a solução é representada pela expansão:
{}{} {}{}∑=
===
£
¤
¥¥
¤¤
FYYFYF
1
~
φ .
As funções peso são então selecionadas como ¦¦ Y=ω (i = 1, 2, 3, ..., N).
Desta forma, a integral dos resíduos será escrita como:
{}{}( ) 0=Ω−=
∫Ω
GYFYY5 §
¨
§§ I/ (i = 1, 2, 3, ..., N).
Isto leva ao sistema de equações [6] {F}T
= {E}T
, para o qual a matriz [6] não é
necessariamente simétrica a menos que o operador / seja auto-adjunto. Neste caso, o método
de Galerkin resulta no mesmo sistema de equações que resultaria da aplicação do método de
Ritz.
O método dos resíduos ponderados, associado com a escolha das funções peso descrita por
Galerkin, é equivalente ao método variacional de Ritz quando a primeira variação do
funcional é zero. Isto ocorre quando o operador / (ou a matriz resultante [6]) é positivo-
definida. Infelizmente, no eletromagnetismo, muitos problemas de interesse são descritos por
operadores não positivo-definidos. Neste caso, o método de Ritz falha em assegurar a
minimização do funcional, já que um ponto estacionário global pode não existir. Contudo a
aplicação do método de Galerkin fornece um sistema discreto e não requer um operador
positivo-definido ou simétrico. A solução é simplesmente um ponto estacionário e não
necessariamente um mínimo.
Para a solução do sistema de equações deve-se impor as condições de contorno. Dois tipos de
condição de contorno são rotineiramente encontradas: a condição de contorno de Dirichlet,
que deve ser explicitamente imposta, e a condição de contorno homogênea de Neumann
( 0ˆ =∂∂ Qφ , derivada normal de φ igual a zero), que é implicitamente satisfeita e conhecida
como condição de contorno natural (não precisa ser explicitamente imposta).
Na técnica de Galerkin, tanto a função de aproximação quanto a função peso são expandidas
utilizando-se as mesmas funções polinomiais. Essas funções recebem o nome de funções de
base ou de forma (1).
No 0pWRGR GRV (OHPHQWRV )LQLWRV 0()

7. o domínio é subdividido em elementos menores.
As funções de base no MEF têm suporte compacto em cada elemento finito, ou seja, seu
range de influência é limitado ao elemento no qual ela está definida e aos seus elementos
vizinhos. Isto acarreta sistemas matriciais altamente esparsos. Em domínios unidimensionais
os elementos finitos são do tipo linha enquanto em domínios bi-dimensionais geralmente
utilizam-se elementos de forma triangular ou quadrangular.

8. 7
1D 2D
nó 1 nó 2
No MEF, as funções de base nodais e escalares assumem valor unitário em cada um dos nós
do elemento finito para o qual elas estão definidas:
( )



=
≠
=
MLS
MLS
U1
¡
¡
/1
/0
δ U¢ = coord. do ponto nodal M
( )XQomR GH %DVH SDUD (OHPHQWR )LQLWR '
Para as funções de base de um elemento finito unidimensional de primeira ordem utilizam-se
polinômios de 1a
ordem.
O elemento unidimensional de 1a
ordem possui dois nós (Q0=2)
As variáveis de estado (φ) podem ser interpoladas neste elemento utilizando:
( ) ∑
=
=
=
2
1
0
£
¤
¤¤
1[ φφ ,
onde φ¥ é o valor da variável de estado no nó L. 1¥ é a iésima
função de interpolação definida
para cada elemento finito.
Nos pontos nodais:
( )
12
12
1212
22
11
[[
[[
[
[
−
−
=⇒−=−



+=
+= φφ
ββφφ
βαφ
βαφ
Substituindo β na segunda equação encontra-se:
( ) ( )
12
212122
2
12
12
222
[[
[[[
[
[[
[
−
−−−
=
−
−
−=−=
φφφφφ
φβφα ,
que resulta
12
2112
[[
[[
−
+−
=
φφ
α .
Elemento
finito tipo
linha
Elemento
finito
triangular
nó 1
nó 2 nó 3
nó 1 nó 2
x1 x2
φ1 φ2

9. 8
Substituindo α e β na expressão de φ, tem-se:
( ) [
[[[[
[[
[
12
12
12
2112
−
−
+
−
+−
=
φφφφ
φ ,
( ) ( ) ( )
12
1221
[[
[[[[
[
−
−+−
=
φφ
φ ,
( ) 2
12
1
1
12
2
φφφ
[[
[[
[[
[[
[
−
−
+
−
−
= .
Assim, as funções de base 1 e 1¡ são dadas por:







−
=
−
−
=
−
=
−
−
=
/
[[
[[
[[
1
/
[[
[[
[[
1
1
12
1
2
2
12
2
1
9DULDomR OLQHDU GH 1¢ H 1£
1 assume valor 1 no nó 1 e zero no nó 2
1¡ assume valor 1 no nó 2 e zero no nó 1
( )



=
≠
=
MLVH
MLVH
[1 ¤
¥
¤
¥
1
0
δ
Na secção VI, será apresentada a formulação escalar do MEF para o estudo de guias ópticos
planares, anisotrópicos e lineares. A formulação considera meios materiais que possuem
tensor permissividade elétrica com elementos diagonais. Para fins de validação do código
computacional a ser implementado, uma equação transcendental, obtida analiticamente, será
apresentada para a determinação das constantes de propagação de guias ópticos planares
simétricos e isotrópicos (secção V). Neste caso, os valores obtidos analiticamente são exatos.
,9 $QiOLVH 0RGDO GH *XLDV ÏSWLFRV 3ODQDUHV
Guias ópticos têm sido utilizados em sistemas de telecomunicação, processamento de sinais,
computação óptica e em sensores de alta precisão. Do ponto de vista da análise
eletromagnética, os guias ópticos podem ser caracterizados por não possuírem bordas
fechadas para a onda eletromagnética e, conseqüentemente, os campos eletromagnéticos
podem se estender na direção transversal até o infinito. O efeito de guiagem, nesses guias
preenchidos com material dielétrico, ocorre pela diferença de índice de refração dos materiais
envolvidos. Embora metais possam estar presentes, suas propriedades físicas têm
comportamento totalmente diferente do observado em freqüências de microondas.
Em guias metálicos, preenchidos com dielétricos, modos TE e TM puros estão presentes. Para
guias ópticos, entretanto, modos com outra configuração de campos são formados e uma
classificação diferente deve ser utilizada. Para curtos comprimentos de onda (da ordem da
dimensão do guia óptico) e pequenas diferenças de índices de refração (guiagem fraca), o
campo elétrico transverso é primariamente paralelo a um dos eixos transversais. Nesse limite,
se o campo elétrico é paralelo ao eixo y, os modos são designados
¦
§¨
( , e se o campo elétrico
1 2
[1 [2
L
1 2
0
1
N1 N2

10. 9
é paralelo ao eixo [, os modos são designados
§¨
( . Os subscritos P e Q representam o
número de máximos na amplitude de campo nas direções [ e , respectivamente.
Os modos (
¡
podem ser bem representados pela aproximação de modos quase-TE, para os
quais o componente de campo (¢ = 0. Neste caso, soluções para a equação de onda podem ser
obtidas para o componente (¡
de campo elétrico. Por outro lado, os modos (
y
podem ser bem
representados pela aproximação de modos quase-TM, com o componente de campo +¢ 0.
Neste caso, as soluções para a equação de onda podem ser encontradas para o componente +¡
de campo magnético.
Guias ópticos planares formados por processos de difusão de metal em substratos como o
LiNbO3 e LiTaO3 são de grande interesse para a construção de moduladores eletroópticos,
chaves, etc. A solução rigorosa é limitada a perfis especiais de distribuição de índices de
refração. O MEF pode solucionar este problema considerando a anisotropia e uma não-
homogeneidade arbitrária do tensor de permissividade elétrica [ε].
Vamos a seguir apresentar a formulação matemática do MEF para guias ópticos planares
anisotrópicos e difusos em meios materiais com tensor permissividade diagonal e sem perdas.
Fig. 1. Guia óptico planar com três camadas dielétricas.
Consideremos um guia de onda óptico planar simétrico de três camadas (Fig. 1) com
propagação do feixe óptico na direção ]. Assumiremos que a estrutura do guia de onda é
homogênea na direção de propagação e que a relação entre índices de refração são: £Q , ¤Q e
¥
Q é ¦
§¨
QQQ ≤ . Se uma onda plana incide na interface superior ou inferior do guia com um
ângulo θ, a constante de fase β, na direção da propagação, será:
θβ VLQQN ©
0=
onde: θ
β
VLQQ
N
Q
=≡
0
é chamado de índice efetivo ou constante de propagação normalizada. Se os ângulos críticos
nas interfaces, W −= e 0 = ,são respectivamente,
então
θθ ≤ , baseada na suposição de que
QQQ ≤ . Entretanto, quando θθ
, a
reflexão total ocorre em ambas as interfaces, resultando na luz sendo transmitida enquanto
∞
∞
Substratoo
Guia Planar Difuso
Cobertura[
-]








= −
Q
Q
VLQ
1
θ 







= −
!
Q
Q
VLQ
1
θ
Índices de Refração:
Cobertura → Q#
Guia → Q$
Substrato → Q%

11. 10
presa no filme fino. Este modo é chamado de modo guiado e
¡
¢
QQQ ≤≤ . Por outro lado,
quando θ é menor que £θ , e ¤
¥
θθθ , a condição para reflexão total não é obedecida na
interface inferior e parte da luz é irradiada para dentro do substrato. Este modo é chamado de
modo de radiação do substrato, neste caso, ¦
§ ¨ ¨©
QQQ ≤≤ . Quando θ torna-se menor e
θθ , a condição de reflexão total não é obedecida por ambas as interfaces superior e
inferior e a luz é irradiada em ambos os lados. Este modo é chamado de modo de radiação do
substrato e cobertura e, neste caso,
QQ ≤ .
9 $ERUGDJHP $QDOtWLFD SDUD (VWXGR GH *XLDV ÏSWLFRV 3ODQDUHV
Para oscilações harmônicas propagando-se em meios materiais dielétricos, isotrópicos e livres
de fontes internas, as equações de Maxwell podem-ser escritas como [3]:
+M( µω−=×∇
(M+ εω+=×∇
0=⋅∇ +
( ) 0=⋅∇ (ε
com ( )
H++
βω −
= , ( )
!!
H((
βω −
= , L = [, , ],
β = constante de propagação e
ω = freqüência angular.
Lembrando que para guias planares não há variação dos campos na direção transversal [
( 0=∂∂ [ ), as equações que envolvem o rotacional dos campos elétrico e magnético podem
ser reescritas como:
#
+M](
0µω−=∂∂
$
%
+M(
0µω=∂∂
'
((
'
(QM+(
2
0εω=∂∂−∂∂
)
0
1
(QM+
2
0εω=∂∂
2
34
(QM+
2
0εω−=∂∂
56
7
+M]((
0µω−=∂∂−∂∂
As equações relacionadas com o termo (×∇ não possuem o componente de
campo 8( (campo elétrico longitudinal), enquanto as equações provenientes de +×∇ não
possuem o componente de campo magnético 9+ (campo magnético longitudinal). Por isso, os
possíveis modos de propagação recebem a denominação de onda transversal elétrica (modo
TE ou modo Ex
) e onda transversal magnética (modo TM ou modo Ey
).
Definindo 1@ A B
P P P= = = para o modo TE, e 21C
C
P Q= , 21D
D
P Q= , 21E
E
P Q= para o
modo TM, a mudança de fase devido à reflexão total será expressa por
( )FF
GGG
NPP αφ 1
tan22 −
=
na interface entre o filme fino e substrato, e
( )FF
HHH
NPP αφ 1
tan22 −
=

12. 11
na interface entre o filme fino e a camada de cobertura superior [3]. Nestas equações,
N corresponde à constante de fase na direção e αs e αc correspondem às constantes de
atenuação e podem ser expressas por :
22 ¡ ¢ ¢¢¢
QQN −= , 22 £¡ ¢ ¢£
QQ −=α , 22 ¤¡ ¢ ¢¤
QQ −=α .
A condição para a existência de um modo guiado é que o desvio de fase total na direção
durante um ciclo, deve ser igual a um múltiplo inteiro de 2 π. Portanto, esta condição pode ser
expressa como segue:
πφφ TWN ¥
¦
§
2222 =−−
onde ,...2,1,0=T , define o modo óptico para o cálculo do autovalor. Por exemplo, T = 0
corresponde ao modo fundamental, enquanto T = 1 e T = 2 correspondem ao segundo e
terceiro modos guiados, respectivamente.
Substituindo as equações para o desvio de fase devido à reflexão (2φs e 2φc) na equação acima
se obtém a seguinte equação de autovalores [3]:
π
αα
T
NP
P
NP
P
WN
¢¢
¤¤
¢¢
££
¢
++= −− 11
tantan
A constante de fase normalizada ( 0NQ¨ © © β= ) de um modo guiado, em uma dada freqüência
angular ω, pode ser calculada a partir da solução da equação transcendental de autovalor
acima.
$ 3URJUDPD SDUD FiOFXOR DQDOtWLFR GRV DXWRYDORUHV Q

13. HP JXLDV
ySWLFRV SODQDUHV VLPpWULFRV H LVRWUySLFRV
O programa apresentado a seguir, foi escrito para o pacote de processamento simbólico
Mathematica.
(* Determinação da constante de propagação de Guias Ópticos Planares Homogêneos e Isotrópicos *)
lambda = Input[”Entre com o comprimento de onda (em microns)” ]; (* Comprimento de Onda em Microns *)
t=Input[”Entre com a espessura do filme (guia) em microns: “]; t = t 0.000001; (* passar para metros *)
tipo = Input[”Modo Ex ou Ey? (x ou y):”]
(* MODO = 0 = Modo Fundamental
= 1 = Segundo Modo
= 2 = Terceiro Modo *)
MODO = Input[”Qual o modo? (0, 1, 2, ...): “]
k0 = N[2 Pi / (lambda 0.000001),10];
neff =.
if [tipo==”x”,
(* MODO Ex *)
nc = 1; nf = 2; ns = 1;
mf = 1; ms = 1; mc = 1,
else,
(* MODO Ey *)
nc = 1; nf = 2; ns = 1;
mf = 1 / nf^2; ms = 1 / ns^2; mc = 1 / nc^2;
];

14. 12
kf = Sqrt[k0^2 nf^2 - neff^2 k0^2];
as = Sqrt[neff^2 k0^2 - k0^2 ns^2 ];
ac = Sqrt[neff^2 k0^2 - k0^2 nc^2 ];
var = ArcTan[(ms as) / (mf kf)] + ArcTan[ (mc ac) / ( mf kf )] + MODO N[Pi];
FindRoot[{ var == kf t },{neff,1.97}, WorkingPrecision - 20 ]
Plot[ ArcTan[(ms as) / (mf kf)] + ArcTan[ (mc ac) / ( mf kf )] + MODO N[Pi] - kf t ,{neff,1.6,2.1}];
9, $ERUGDJHP 1XPpULFD )RUPXODomR GR 0() SDUD (VWXGR GH
*XLDV ÏSWLFRV 3ODQDUHV $QLVRWUySLFRV H 1mR+RPRJrQHRV
A seguir, será apresentada a formulação matemática do MEF escalar para o estudo modal de
guias ópticos planares, anisotrópicos, simétricos ou não e não-homogêneos [4]-[7].
Como caso particular, serão considerados meios materiais para os quais a permissividade
elétrica pode ser representada como:
[ ] [ ]
( )
( )
( )









==
Q
Q
Q
¡
¢
£
2
2
2
0
00
00
00
1
εε
ε
Consideremos uma onda propagando-se harmonicamente na direção longitudinal ]. Neste
caso, as equações de Maxwell podem ser escritas como:
Substituindo as expressões para os campos elétrico e magnético nas equações de Maxwell e
suprimindo o fator ( )¤
¥
¦
H
βω −
, tem-se:
( ) 0.
0.
=∇
=∇
+=×∇
−=×∇
(
+
(M+
+M(
ε
εω
µω
Com
( )
( )§
¨
©
§
¨
©
H
H
((
++
βω
βω
−
−
=
=
β = constante de propagação
ω = freqüência angular
(QM
+
[
+
(QM+M
[
+
(QM+M
+
2
0
2
0
2
0
εω
εωβ
εωβ
−=
∂
∂
−
∂
∂
−=+
∂
∂
+=+
∂
∂
q
r
s
( ) ( ) 02
22
=−
∂
∂
+
∂
∂
=
∂
∂
−
∂
∂
(QM
(Q
[
(Q
+M
+
[
+
β
β
t
u
+M
(
[
(
+M(M
[
(
+M(M
(
0
0
0
µω
µωβ
µωβ
−=
∂
∂
−
∂
∂
=+
∂
∂
−=+
∂
∂
n
o
p

15. 13
9DPRV GHWHUPLQDU D (TXDomR GH 2QGD SDUD 0RGRV (
FDPSR (¡ {

16. Isolando os componentes +¢ e +£ das equações (2) e (3), respectivamente, obtém-se:
Substituindo estes componentes de campo na equação (4), obtém-se:
Lembrando que: 00
22
0 εµω=N
¤¤¤
¤
(QN(
( 22
0
2
2
2
−=−
∂
∂
β (TXDomR GH RQGD SDUD 0RGR (
9DPRV GHWHUPLQDU D (TXDomR GH 2QGD SDUD 0RGRV (
¥
FDPSR +¦ {

17. Isolando os componentes de campo Ey e Ez das equações (6) e (7), respectivamente, obtém-
se:
Substituindo esses componentes na equação (1) resulta:
[
(M
(+
§
¨©
∂
∂
−=
00 µωµω
β






∂
∂
−
∂
∂
=
(
[
(
M+
0
1
µω
Para guias planares não há confinamento de
campo ao longo da direção transversal x.
Pode-se então anular as derivadas de campo
na direção x, pois este campo é constante
nesta direção. Além disso, pela
aproximação de modo Ex
→ o componente
Ey ≡ 0.
+
Q
M
(
Q
+
(
∂
∂
=
−=
2
0
2
0
εω
εω
β
==+





∂
∂
−
∂
∂
(QM(M
(
M
2
0
00
1
εω
µω
β
β
µω
==+
∂
∂
−
(Q(
( 2
0
0
2
2
2
0
1
εω
µω
β
µω
(Q(
( 2
00
22
2
2
εµωβ −=−
∂
∂

18. 14
0
0
11
0
00
2222
02
0
2
2
0
02
0
2
0
=+−





∂
∂
∂
∂
=+−





∂
∂
∂
∂
=+−







∂
∂
∂
∂
−− ¡
¢
¡
¢
¡
¢
++Q
+
Q
+M
Q
+
+
Q
+M
Q
+
M
+
Q
M
µεωβ
µω
εω
β
εω
µω
εω
β
β
εω
02
0
222
=+−





∂
∂
∂
∂ −− ££¤
£
¥ +N+Q
+
Q
β (TXDomR GH RQGD SDUD 0RGR (
¦
Escrevendo as equações de onda de forma compacta, tem-se:
Aplicando o Método dos Resíduos Ponderados [5]:
φ é a função teste
As condições de contorno são:
( ) .0.
ˆˆ
21
0
0
2
0
2
∫∫
∫
=−+





∂
∂
−
∂
∂
+
+








+−











∂
∂
∂
∂
§©¨ ¨ !$#%('('
)
G6:G6
QQ
:
GN%
$
:
φφ
φφ
φφβ
φ
Onde ::: e, são funções peso inicialmente arbitrárias.
2
1
1
0
0
Q
%
$
(
=
=
=
=⇒ φ
1
(PRGR
1
2
2
=
=
=
=⇒
−
−
Q%
Q$
+
2
3
4φ
5
(PRGR
02
0
2
=+−





∂
∂
∂
∂
φφβ
φ
N%
$
)(0
ˆ
)(0ˆ
1
2
6HPRJrQHDKRP1HXPDQQ
Q
6HPRJrQHDKRP'LULFKOHWQ
=
∂
∂
=×
φ
φ

19. 15
Impondo a condição de contorno de Dirichlet na superfície 62, tem-se a solução conhecida
0φφ = . Assim, a integral com o termo : pode ser anulada.
Vamos analisar a primeira integral separadamente.
A derivada de segunda ordem mostra que a equação está escrita em sua forma “forte”. Neste
caso, seria necessário utilizar elementos finitos da classe C1
(segunda ordem de aproximação)
ou superior.
Para baixar este requisito utiliza-se o teorema de Green e escreve-se o termo na forma “fraca”.
∫∫∫ +=ΩΩ
∇+Ω∇−=Ω∇∇
21
ˆ.. 2
G6QYXGYXGYX .
O primeiro termo integral será:
∫ ∫∫ ∂
∂
+
∂
∂
∂
∂
=





∂
∂
∂
∂
G
$:G
$
:G
$
:
2
2
.
φφφ
,
fazendo:
( )
∫∫∫ +ΩΩ
∇+Ω∇∇−=Ω
∂
∂
21
ˆ..2
2
¡¡
G6Q$:G$:G
$: φφ
φ
.
Resultando a seguinte equação de resíduo:
( )
.0.
ˆˆ
ˆ.
1
21
02
0
2
=





∂
∂
−
∂
∂
++−
−
∂
∂
+
∂
∂
∂
∂
−
∂
∂
∂
∂
∫∫∫
∫∫∫ +
¢££
¢¢££
G6
QQ
:G:NG%:
G6QM
$:G
$
$:
G
$
:
φφ
φφβ
φφ
Escrevendo :$: −= , resulta:
0.
ˆ
ˆ.
11
=
∂
∂
−
∂
∂
∫∫ ¤¤
G6
Q
:$G6QM
$:
φφ
.
Assim temos:
( )
.0.
ˆ
ˆ.
1
2
02
0
2
=
∂
∂
++−
−
∂
∂
+
∂
∂
∂
∂
−
∂
∂
∂
∂
∫∫∫
∫∫∫
¥§¦©¨
! $#% ¦©'
G6
Q
:$G:NG%:
G6QM
$:G
$
$:
G
$
:
φ
φφβ
φφ
Para o problema de propagação de onda a condição de contorno sobre a superfície 61 é a
condição de Neumann homogênea 0
ˆ
0
=
∂
∂
Q
φ
. Desta forma, a integral sobre 61 é nula.
φ=
=
Y
$:X

20. 16
Assumindo 0=: sobre a superfície de Dirichlet 62 resulta:
∫∫∫ =−+
∂
∂
∂
∂
−=
¡
G:%G:NG
:
$5 .022
0 φβφ
φ
Esta equação fornece a base para a solução da equação de Helmholtz não homogênea pelo
método dos resíduos ponderados, em termos de uma função teste φ construída para cada
elemento individual [5].
Existem muitas maneiras de se selecionar as funções :. A mais comum, no método dos
elementos finitos, é utilizar para : o mesmo conjunto de funções de base { }1 utilizadas na
interpolação da função teste φ no interior de cada elemento finito. Esta escolha para as
funções peso no método dos resíduos ponderados, e suas conseqüências, é denominada
método de Galerkin.
Assumimos agora a seguinte aproximação:
{ }{ } { }{ }∑∑ ==
====
00
11
¢
£
¤
££
¢
£
¤
££
Z1Z1:11 φφφ
Vamos considerar que os parâmetros $, % e são constantes no interior de cada elemento
finito.
{ } { } { } { } { }{ }
{ } { }{ } 02
2
0
=−
−+
∂
∂
∂
∂
−
∫
∫∫
¥
¦¦
¥
¦¦
¥
¦
¦
G11%
G11NG
1
1
$
φβ
φφ
mas: 2
0
22
02
0
2
2
NQN
N
§ ¨ ¨
=





= ββ
Escrevendo na forma matricial obtém-se:
[ ]{ } [ ]{ }
©
©
0Q) φφ 2
=
com [ ] [ ] [ ]21 ))) −=
[ ] { } { }
∫=
G11N)
2
01
.02
0
2
=+−
−





∂
∂
∂
∂
+
∂
∂
∂
∂
−
∂
∂
∂
∂
∫∫
∫∫
G:NG:%
G
$
:
:
$G
$
:
φφβ
φφφ

21. 17
[ ] { } { }
∫ ∂
∂
∂
∂
=
¡
G
1
1
$)
2
[ ] { } { }
∫=
¢
£
G11%N0
2
0
Para elementos finitos do tipo Lagrange de primeira ordem de aproximação polinomial, tem-
se:
3ULPHLUD RUGHP
[ ]
[ ]
[ ] 





=






−
−
=






=
21
12
6
11
11
21
12
6
2
0
2
2
0
1
%/N
0
/
$
)
/N
)
$ ([HPSOR GH $SOLFDomR
Com a finalidade de validar as implementações do MEF para o estudo de guias ópticos
planares, foram realizados vários cálculos comparando os resultados obtidos com o MEF e
com a abordagem analítica descrita na secção (V). A solução analítica fornece valores exatos
para a constante de propagação normalizada de guias ópticos planares isotrópicos e
simétricos, ou seja, guias onde a camada de cobertura e de substrato têm a mesma espessura e
índices de refração.
DVR GH (VWXGR *XLD 3ODQDU +RPRJrQHR ,VRWUySLFR H
6LPpWULFR
A seguir, são apresentados os resultados para as simulações do guia óptico planar. Na análise
dos resultados foram utilizados parâmetros normalizados para a constante de propagação (%) e
para a freqüência de operação (ν), por apresentarem maior sensibilidade às mudanças
geométricas da estrutura do guia e às diferenças de índices de refração.
22
22
220
,
h
¤¥
¤¦ § §
¤¥
QQ
QQ
%QQ
N
−
−
=−=
π
ν ,
1 2
1
Numeração local

22. 18
onde N0 representa o número de onda no espaço livre, h é a espessura da camada do guia
(filme fino ou guia difuso), Q ¡ ¡ é a constante de propagação normalizada do modo óptico e Q¢
e Q£ são os índices de refração da camada do guia e da camada de cobertura, respectivamente.
As Figs. 2a e 2b mostram as curvas de dispersão para os três primeiros modos do guia planar
(% x ν). A Fig. 2a apresenta os valores para os modos Ex
e a Fig. 2b apresenta os valores para
os modos Ey
. As curvas com linha sólida representam os valores obtidos com a aplicação do
MEF enquanto os pontos representam os valores obtidos pela solução analítica. Os
parâmetros utilizados nessa simulação foram: h = 3 µm, Q¢ = 1, Q£ = 2 e hc = hs = 5 µm sendo
hc e hs as espessuras da camada de cobertura e camada de substrato, respectivamente. Como
se pode observar das Figs 2a e 2b, os valores coincidem para todo o intervalo de freqüências
utilizado no estudo. Esses cálculos permitiram validar a implementação do programa baseado
no MEF.
As Figs. 3a e 3b apresentam os valores obtidos, pela implementação do MEF, para a constante
de propagação normalizada (%) em função da espessura da camada do guia, para os modos Ex
e Ey
, respectivamente. Os parâmetros utilizados nessa simulação foram: λ = 1 µm, Q¢ = 1,
Q£ = 2 e hc = hs = 5 µm.
Fig. 2 Curvas de dispersão dos três primeiros modos guiados em um guia planar isotrópico e simétrico. A Fig. 2a
apresenta os resultados para modos Ex
e a Fig. 2b apresenta os resultados para modos Ey
. As linhas sólidas
representam os valores obtidos pelo MEF e os pontos representam os valores obtidos pela solução analítica.
Fig. 3 Constante de propagação normalizada (%), para os três primeiros modos guiados, em função da espessura
(h) do filme (guia). A Fig. 3a apresenta os resultados para modos Ex
e a Fig. 3b apresenta os resultados para
modos Ey
. As linhas sólidas representam os valores obtidos pelo MEF.
As Figs. 4a e 4b apresentam os valores obtidos, pela implementação do MEF, para a constante
de propagação normalizada (%) em função do índice de refração da camada do guia, para os
modos Ex
e Ey
, respectivamente. Os parâmetros utilizados nessa simulação foram: λ = 1 µm,
Q¢ = 1, h = 3 µm e hc = hs = 5 µm.
¤ ¥ ¦ § ¦©¨ §
! # ! $ % ! !
' ¥©
' ¥ (
' )©
' ) (
¦©' ©
0 12
345 2
46
7 68
918
5@
5A
B1 2
1
9C
5
DE F
5
7 5
Primeiro Modo
Segundo Modo
Terceiro Modo
Modo E
x
2a
G H I©P I Q PR
S T U V W X Y ` a b Y c T d b e a f b g b
Rh i p
Rh H©R
Rh H p
Rh q©R
Rh q p
I©h R©R
r st
uvw t
vx
y x€
s€
w‚
wƒ
„s t
s
…
w
†‡ ˆ
w
y w
Primeiro Modo
Segundo Modo
Terceiro Modo
Modo E
y
2b
‰  ‘ ’ “
”–•–—™˜d•e•–f–g hji–hlkmh™noheiphji–˜rq™s t no˜
u©v ’
u©v “
u©v w
u©v x
u©v y
u©v z
‰ v u
{ |}
~€ }

‚ ƒ
„|ƒ
€…
۠
€
|}
|
„‡
€
ˆ‰ Š
€
‚€ ‹
Œ
Primeiro Modo
Segundo Modo
Terceiro Modo
Modo E
x
~
3a
 Ž   ‘
’ “ ” • “ “ – — ˜ ™ ˜ š ˜ › ˜ ™ ˜ ™ • œ  ž › •
Ÿ 
Ÿ 
Ÿ ‘
Ÿ ¡
Ÿ ¢
Ÿ £
Ÿ ¤
© Ÿ
¥ ¦§
¨©ª §
©«
¬ «­
®¦­
ª¯
ª°
±¦ §
¦
®²
ª
³´ µ
ª
¬ ª
Primeiro Modo
Segundo Modo
Terceiro Modo
Modo E
y
3b
¶ · ¸º¹
¶ · ¸º¹

23. 19
Fig. 4 Constante de propagação normalizada (%), para os três primeiros modos guiados, em função do índice de
refração da camada do filme (guia). A Fig. 4a apresenta os resultados para modos Ex
e a Fig. 4b apresenta os
resultados para modos Ey
. As linhas sólidas representam os valores obtidos pelo MEF.
9,, $QiOLVH 1XPpULFD GH *XLDV ÏSWLFRV 3ODQDUHV $QLVRWUySLFRV H
1mR+RPRJrQHRV
$ *XLD 3ODQDU )RUPDGR SRU 3URFHVVR GH 'LIXVmR 7L/L1E2

24. Guias ópticos formados por difusão de íons de Ti em substratos de LiNbO3 são muito
utilizados em circuitos de óptica integrada. Os parâmetros de difusão determinam os modos
ópticos suportados pela estrutura e o grau de confinamento. Na definição dos guias ópticos
planares, os seguintes parâmetros de fabricação foram considerados: a espessura inicial do
filme de Ti (H), a temperatura de difusão (T) e o tempo de difusão (t).
Para guias planares do tipo Ti:LiNbO3, os índices de refração na região de difusão são dados
por:
( ) ( )[ ] 







−−∆++= 2
y
2
2
b
2
sb
2
b
2
oe,
d
y
expnnnn,yn oe,oe,oe,oe,
λ ,
onde: H R denotam os eixos extraordinário e ordinário respectivamente, é a coordenada de
um ponto no substrato, G¡ é a profundidade de difusão, Q¢ é o índice de refração do substrato
e ∆Q£ é a variação do índice de refração superficial com o comprimento de onda (λ). ¤
¥¦
§Q∆ é
fornecido em função de H e de alguns parâmetros de ajuste:
( ) ( ) ( )
oe,
oe,oe,
oe,
yy
10s
d
H
d
H
BBn
α
λλλ
















+=∆ ,
,53.0,83.0 == ¨© αα ( ) 6.16.0 ≤≤ Pµλ ,
( ) ,171.0430.0385.0 2
0 λλλ +−=%
( ) ,490.2850.3130.9 2
1 λλλ −+=%
( ) ,0071.00315.00653.0 2
0 λλλ +−=%
( ) 2
1 3480.04640.04780.0 λλλ −+=% .
! # $% % % ! #% $%'
( )1032 4657085@9 5BA 9 C6D6E6FG)6C746CIHPCQ08C708F@R3S82 C
!
$
#
!
$
T UV
WXY V
X`
a `
bcU
bYd
Ye
fU V
U
cg
Y
hi p
Y
a Y q
r
Modo E
y
st ust vst wst xst y%vt u%vt v%vt wvt x%vt y%€t u
 ‚1ƒ3„ …6†7ƒ8†@‡ †Bˆ ‡ ‰66‘6’G‚6‰7…6‰I“P‰Qƒ8‰7ƒ8’@”3•8„ ‰
ut u
ut w
ut y
st v
st x
vt u
vt w
vt y
– —˜
™de ˜
df
g f
hi—
hej
ek
l— ˜
—
i
me
no p
e
g e q
r
Modo E
x
4a 4b

25. 20
O coeficiente de difusão ' , a profundidade de difusão G e a profundidade de mudança no
perfil de índice de refração G ¢¡ e G ¤£ podem ser calculados por:
( )'' ¥¦
§
¨© 0exp0 −= L H R
W'G 2=
G
G
α
=
onde ' 0 é a constante de difusão, ( 0 é a energia de ativação e . = 8,61735[10−5
(eV/o
K) é a
constante de Boltzmann. Essas constantes para o guia Ti:LiNbO3, são apresentadas na
Tabela I.
A dispersão nos índices de refração do substrato de LiNbO3 é considerada utilizando a
equação de Sellmeier apresentadas a seguir, considerando o comprimento de onda (λ) em µm:
2
2
2
027169.0
04750.0
11768.0
9048.4 λ
λ
−
−
−=!
Q ,
2
2
2
021950.0
044432.0
099169.0
5820.4 λ
λ
−
−
−=#
$Q .
Curvas de dispersão foram obtidas para modos Ex
e Ey
em substrato de LiNbO3 com cortes X
e Z, respectivamente, e propagação ao longo do eixo cristalino principal Y.
Tabela I: Coeficientes da lei de Arrhenius para guias do tipo Ti:LiNbO3
'%' (µm2
/ h) 5.0 e+9
'R (µm2
/ h) 1.35 e+8
(H (eV) 2.60
(R (eV) 2.22
% DVR GH (VWXGR *XLD ÏSWLFR 3ODQDU 1mR+RPRJrQHR
$QLVRWUySLFR H 1mR6LPpWULFR JXLD WLSR 7L/L1E2(

26. A seguir, serão apresentados alguns resultados obtidos para a simulação das características
modais de um guia óptico planar formado pela difusão de ions de Ti em substrato de LiNbO3.
Os parâmetros utilizados foram: comprimento de onda λ=1 µm, modo óptico Ex
, tipo de guia
→ difuso (Ti:LiNbO3), espessura da camada de cobertura de 5 µm, índices de refração da
camada de cobertura Q) Q0 Q1 =1, espessura da camada de substrato de 20 µm, substrato de
LiNbO3 com corte cristalino X (corte-X) e espessura do filme fino de Ti, utilizado para
difusão, igual a 80 nm. A Fig. 5a apresenta os valores obtidos para o índice efetivo dos três
primeiros modos de propagação em função do tempo de difusão, para uma temperatura de
difusão T=1050o
C. A Fig. 5b apresenta os valores de índice efetivo em função da temperatura
de difusão, para 6 horas como tempo de difusão.

27. 21
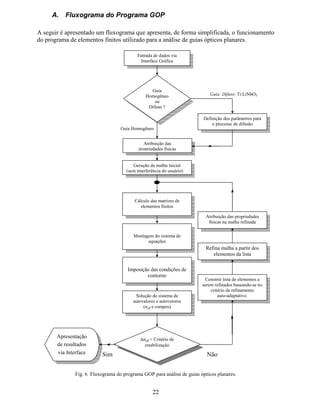
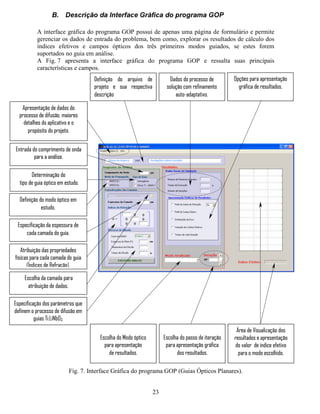
Fig. 5 Valores para o índice efetivo (Q ¡ ¡ ), dos três primeiros modos guiados, em função de parâmetros do
processo de difusão do filme de Ti em substratos de LiNbO3. Fig. 5a Apresenta os valores de Q ¡ ¡ em função do
tempo de difusão e a Fig. 5b apresenta valores de Q ¡ ¡ em função da temperatura de difusão.
9,,, 3URJUDPD SDUD $QiOLVH 0RGDO GH *XLDV ÏSWLFRV 3ODQDUHV H
'HVFULomR GD ,QWHUIDFH *UiILFD SDUD (QWUDGD GH 'DGRV H
9LVXDOL]DomR *UiILFD GH 5HVXOWDGRV
Como parte deste trabalho, foi projetado e implementado um programa para a análise modal
de guias ópticos planares de três camadas dielétricas, que permite levar em consideração
anisotropias diagonais do tensor permissividade elétrica e não-homogeneidades. O programa,
denominado GOP (*uias Ïpticos 3lanares), é uma implementação do Método dos Elementos
Finitos para o estudos de guias planares e inclui a técnica de refinamento auto-adaptativo para
discretização de um domínio unidimensional visando o cálculo dos três primeiros modos
ópticos guiados.
O programa GOP foi implementado no ambiente de programação do software Matlab. O
Matlab conta com o recurso de auxílio à criação de interfaces gráficas, uma extensa biblioteca
de funções matemáticas e opção para geração automática de código em linguagem C e C++,
além de uma biblioteca de funções matemáticas e gráficas para criação de códigos
compilados.
Para facilitar a utilização do programa GOP, foi criada uma interface gráfica simples que
gerencia a entrada dos dados para a simulação e apresenta os resultados graficamente.
¢¤£¦¥ ¢¨§ £ ©¤¥¨¥¨¥ © ¥¨¤£ ©¤¥¤£¦¥ ©¤¥¨§¤£ ©¨©¤¥¨¥
! # %$%('
¦) © £
¦) ©¤0
¦) ©¤§
¦) ©¤1
¦) ©¤¢
2 3
45 6
7
89
7@5 A
B
2 5 8 11 14 17 20
Tempo (h)
2.15
2.16
2.17
2.18
IndiceEfetivo
D E

28. 22
$ )OX[RJUDPD GR 3URJUDPD *23
A seguir é apresentado um fluxograma que apresenta, de forma simplificada, o funcionamento
do programa de elementos finitos utilizado para a análise de guias ópticos planares.
Fig. 6 Fluxograma do programa GOP para análise de guias ópticos planares.
Montagem do sistema de
equações
Imposição das condições de
contorno
Atribuição das
propriedades físicas
Geração da malha inicial
(sem interferência do usuário)
Cálculo das matrizes de
elementos finitos
Definição dos parâmetros para
o processo de difusão
Guia
Homogêneo
ou
Difuso ?
Entrada de dados via
Interface Gráfica
Solução do sistema de
autovalores e autovetores
(Q ¡ ¡ e campos)
∆Q ¡ ¡ Critério de
estabilização
Apresentação
de resultados
via Interface
Constrói lista de elementos a
serem refinados baseando-se no
critério de refinamento
auto-adaptativo.
Refina malha a partir dos
elementos da lista
Atribuição das propriedades
físicas na malha refinada
*XLD 'LIXVR: Ti:LiNbO3
Guia Homogêneo
Sim Não

29. 23
% 'HVFULomR GD ,QWHUIDFH *UiILFD GR SURJUDPD *23
A interface gráfica do programa GOP possui de apenas uma página de formulário e permite
gerenciar os dados de entrada do problema, bem como, explorar os resultados de cálculo dos
índices efetivos e campos ópticos dos três primeiros modos guiados, se estes forem
suportados no guia em análise.
A Fig. 7 apresenta a interface gráfica do programa GOP e ressalta suas principais
características e campos.
Fig. 7. Interface Gráfica do programa GOP (Guias Ópticos Planares).
(VSHFLILFDomR GRV SDUkPHWURV TXH
GHILQHP R SURFHVVR GH GLIXVmR HP
JXLDV 7L/L1E2 ¢¡
$WULEXLomR GDV SURSULHGDGHV
ItVLFDV SDUD FDGD FDPDGD GR JXLD
ÌQGLFHV GH 5HIUDomR

30. (VSHFLILFDomR GD HVSHVVXUD GH
FDGD FDPDGD GR JXLD
(VFROKD GD FDPDGD SDUD
DWULEXLomR GH GDGRV
'HILQLomR GR PRGR ySWLFR HP
HVWXGR
(QWUDGD GR FRPSULPHQWR GH RQGD
SDUD D DQiOLVH
'DGRV GR SURFHVVR GH
VROXomR FRP UHILQDPHQWR
DXWRDGDSWDWLYR
'HILQLomR GR DUTXLYR GH
SURMHWR H VXD UHVSHFWLYD
GHVFULomR
2So}HV SDUD DSUHVHQWDomR
JUiILFD GH UHVXOWDGRV
$SUHVHQWDomR GH GDGRV GR
SURFHVVR GH GLIXVmR PDLRUHV
GHWDOKHV GR DSOLFDWLYR H R
SURSyVLWR GR SURMHWR
'HWHUPLQDomR GR
WLSR GH JXLD ySWLFR HP HVWXGR
(VFROKD GR 0RGR ySWLFR
SDUD DSUHVHQWDomR
GH UHVXOWDGRV
(VFROKD GR SDVVR GH LWHUDomR
SDUD DSUHVHQWDomR JUiILFD
GRV UHVXOWDGRV
ÉUHD GH 9LVXDOL]DomR GRV
UHVXOWDGRV H DSUHVHQWDomR
GR YDORU GH tQGLFH HIHWLYR
SDUD R PRGR HVFROKLGR

31. 24
3DUkPHWURV GH (QWUDGD
No programa GOP, os parâmetros de entrada estão agrupados em uma região delimitada por
uma caixa de cor verde, que recebeu o nome 5HTXLVLWRV GH $QiOLVH. A Fig. 8 apresenta
detalhes dos elementos de interface associados à entrada de dados.
Fig. 8 Campos para definição dos parâmetros de entrada do programa GOP.
RPSULPHQWR GH 2QGD Campo de entrada para comprimento de onda em mícron. O
intervalo válido para a entrada é 0,6 ≤ λ (µm) ≤ 1,6. Para guias ópticos difusos (Ti:LiNbO3) a
dispersão do valor de índice de refração do substrato ( Q(λ) ) é considerada através da equação
de Sellmeir, como descrito na secção VII - A.
0RGR GH SURSDJDomR Neste elemento gráfico, o usuário deve escolher o tipo de modo
óptico para a análise. Guias ópticos dielétricos com pequenas diferenças de índices de
refração (aproximação de guiagem fraca) comportam a propagação de modos ópticos com
duas polarizações denominadas: modos Ex
e Ey
.
7LSR GH *XLD As opções para este item são: Guia Homogêneo e Guia Difuso
(Ti:LiNbO3). Deve-se ativar uma das opções para que o aplicativo possa dar seqüência às
especificações das camadas.
1
3
2
4
5
6
7
8
9
10
11
1
2
3

32. 25
(VFROKHU DPDGD Um menu “popup” permite a escolha da camada para atribuição de
propriedades físicas. O menu é contextualizado para as opções de guia homogêneo e difuso.
Todas as camadas devem ser selecionadas antes que o programa permita o prosseguimento da
análise numérica. Caso haja necessidade de alterar os dados referentes a alguma camada,
basta selecioná-la para acessar os valores já atribuídos.
(VSHVVXUD GD DPDGD Este campo permite a atribuição da espessura de cada camada
do guia planar. A espessura deve ser fornecida em mícron.
3URSULHGDGHV ItVLFDV 7HQVRU GH ËQGLFHV GH 5HIUDomR Este campo permite a
atribuição de índices de refração para camadas homogêneas do guia planar. O aplicativo
permite tratar meios materiais com anisotropia diagonal do tensor de índices de refração.
3URFHVVR GH 'LIXVmR RUWH GR /L1E2 No caso de guias difusos do tipo Ti:LiNbO3,
deve-se definir a orientação dos eixos cristalinos do substrato de LiNbO3 com relação ao
sistema de referência utilizado para a equação de onda. Na área de estudo de estado sólido, a
orientação dos eixos cristalinos recebe o nome de RUWH. No caso de substratos de LiNbO3
com Corte-X, tem-se que o eixo cristalino associado ao índice de refração Q¡ coincide com o
eixo cartesiano , enquanto o eixo cristalino associado ao índice de refração Q¢ coincide com o
eixo cartesiano [. No caso do Corte-Z, tem-se que o eixo cristalino associado ao índice de
refração Q¡ coincide com o eixo cartesiano [, enquanto o eixo cristalino associado ao índice de
refração Q¢ coincide com o eixo cartesiano . Em todas as análises do programa GOP, será
considerado que a onda propaga-se ao longo do eixo cristalino Y, que coincide com o eixo
cartesiano ].
3URFHVVR GH 'LIXVmR (VSHVVXUD GR )LOPH GH 7LWkQLR Neste campo, o usuário define
a espessura do filme fino de titânio a ser utilizado no processo de difusão em substrato de
LiNbO3. As espessuras devem ser fornecidas em nanômetro (nm).
3URFHVVR GH 'LIXVmR ± 7HPSHUDWXUD GH 'LIXVmR Campo para definição da
temperatura utilizada para o processo de difusão. A temperatura deve ser fornecida em graus
Celsius (o
C).
3URFHVVR GH 'LIXVmR ± 7HPSR GH 'LIXVmR Campo para definição do tempo total
utilizado para o processo de difusão. O tempo de difusão deve ser fornecido em horas (h).
$WULEXLomR GH 9DORUHV j DPDGD H ([HFXWDU $QiOLVH Ao final das atribuições de
cada camada, o botão será ativado e apresentará a mensagem: $WULEXLU 9DORUHV j DPDGD.
Pressionando esse botão, os valores atribuídos para os campos de entrada, para a camada
escolhida, serão armazenados. Após todas as camadas receberem os dados de entrada, o botão
passará a apresentar a seguinte mensagem: ([HFXWDU $QiOLVH e quando pressionado, serão
iniciados os cálculos para a análise modal do guia óptico planar.
4
5
6
7
8
9
10
11

33. 26
2So}HV SDUD 9LVXDOL]DomR *UiILFD GH 5HVXOWDGRV
No programa GOP, as opções para apresentação de resultados estão agrupadas em uma
região, delimitada por uma caixa de cor vermelha, que recebeu o nome 5HVXOWDGRV. A Fig. 9
apresenta detalhes dos elementos de interface associados à apresentação de resultados.
Fig. 9 Campos para definição das opções para apresentação de resultados no programa GOP.
1~PHUR GH (OHPHQWRV *HUDGRV Após a análise, o aplicativo apresenta o número
total de elementos finitos gerados durante o processo de refinamento auto-adaptativo.
7HPSR GH ([HFXomR Este campo apresenta o tempo total de simulação do guia
planar. O intervalo de tempo é apresentado em segundos (s).
1~PHUR GH ,WHUDo}HV Este campo apresenta o número total de iterações do processo
auto-adaptativo utilizado para a simulação das características modais do guia óptico planar,
satisfazendo o critério de precisão adotado (estabilização dos valores de índice efetivo até a
sétima casa decimal).
12
13
14
16
22
15
17
18
19
20
21
12
13
14

34. 27
$SUHVHQWDomR *UiILFD GRV 5HVXOWDGRV Os campos 15 a 22 permitem escolher qual resultado
será apresentado na região destinada a gráficos na interface.
3 HUILO GR ËQGLFH GH 5HIUDomR Opção para selecionar apresentação do perfil de
índice de refração em forma de gráfico (índice versus coordenada do baricentro do elemento
finito). Esta opção deve ser associada ao campo 16.
(V FROKD GR ËQGLFH GH 5HIUDomR Opção para definir qual dos índices de refração
será apresentado de forma gráfica (índice versus coordenada do baricentro do elemento
finito). Esta opção é contextualizada para os problemas de guia homogêneo (Q , Q¡ e Q¢ ) e
guia difuso (Q £ e Q ¤ ).
3 HUILO GH DP SR ÏSWLF R Opção para selecionar a apresentação do perfil de campo
óptico do modo escolhido no campo 21. Os valores de campo são relativos ao passo de
iteração escolhido no campo 22.
'LV WULEXLomR GH (UURV Opção para selecionar a apresentação da distribuição de
erros relativos ao processo de refinamento auto-adaptativo da malha de elementos finitos.
Esses erros são calculados para cada elemento finito considerando-se o comprimento do
elemento e o gradiente do campo óptico no elemento. A distribuição de erros relativos
resultante é utilizada para decidir quais elementos finitos deverão ser subdivididos durante
um passo de refinamento auto-adaptativo da malha. A distribuição de erros pode ser
visualizada para cada um dos três possíveis modos guiados (campo 21), em cada passo de
iteração (campo 22).
9DULDomR GRV ËQGLFHV (IHWLYRV Opção para selecionar a apresentação do valor do
índice efetivo (Q £ ¥ ¥ ) em função do passo de iteração do processo auto-adaptativo da malha de
elementos finitos. É possível a apresentação do valor de Q£ ¥ ¥
para cada modo escolhido no
campo 21.
7HP S R GH DGD ,WHUDomR Opção para selecionar a apresentação do intervalo de
tempo de processamento em função do número da iteração do processo de refinamento auto-
adaptativo da malha de elementos finitos.
0 RGR $QDOLV DGR Opção de escolha do modo óptico para apresentação gráfica de
resultados. Três modos são permitidos, sendo que o modo fundamental é o que possui maior
valor de índice efetivo.
,WHUDomR Opção para seleção da iteração (passo do refinamento auto-adaptativo da
malha de elementos finitos) para apresentação gráfica de resultados.
15
16
17
18
19
20
21
22

35. 28
9LVXDOL]DomR GH 5HVXOWDGRV
Para demonstrar a utilização do programa GOP e a forma como os resultados podem ser
apresentados, foi realizada uma simulação para a determinação dos possíveis modos de
propagação em um guia óptico planar difuso formado pela difusão de Titânio (Ti) em
substrato de Niobato de Lítio (LiNbO3) . Os parâmetros utilizados na simulação foram:
• Comprimento de onda de 1 µm,
• Modo Ex
• Guia Difuso Ti:LiNbO3
• Camada de cobertura de 5 µm de espessura
• Índices de refração da camada de cobertura: Q =Q¡ =Q¢ =1
• Camada de substrato de 40 µm de espessura
• Processo de difusão:
• Corte-X
• Espessura do filme de Ti : H=80 nm
• Temperatura de difusão: T=1050 o
C
• Tempo de difusão: t=6 h
A malha inicial de elementos finitos é automaticamente gerada pelo programa GOP e consta
de 15 elementos em cada uma das camadas do guia difuso (cobertura e substrato). Após o
processo de refinamento auto-adaptativo, que finalizou após 12 iterações, o número total de
elementos finitos na malha é de 3687 e o tempo total de CPU utilizado foi de 67,726
segundos, esses resultados são apresentados na interface, como mostrado na Fig. 10.
Fig. 10 Apresentação de dados relativos ao número total de elementos na malha, tempo de processamento e
número total de iterações.
Os valores inseridos como parâmetros para o processo de difusão de Titânio e o comprimento
de onda possibilitam calcular o perfil de índices de refração extraordinário (Q¡ ) e ordinário
(Q¢ ) na região em que o guia difuso é formado. O perfil de índices de refração Q¡ e Q¢ pode ser
visualizado no campo de gráficos acionando a opção 3HUILO GR ËQGLFH GH 5HIUDomR e
escolhendo qual o índice desejado NE ou NO (Fig.11). A distribuição de índices pode ser
visualizada para cada passo de refinamento auto-adaptativo.
Fig. 11 Botão para escolha da opção de visualização do perfil de índices de refração.

36. 29
Os perfis de índices de refração, para o caso simulado, são apresentados nas Figs. 12a e 12b.
Pode-se notar que no processo de difusão de Ti em LiNbO3 a maior variação (aumento do
valor em relação ao substrato puro) ocorre para o índice de refração extraordinário.
Fig. 12 Apresentação do perfil de índices de refração. A Fig. 12a apresenta os índices extraordinários e a Fig.
12b apresenta os índices ordinários.
Na análise modal de guias ópticos é muito importante visualizar a distribuição de campo
óptico para cada modo de propagação. Com os perfis dos modos, pode-se identificá-los e
classificá-los segundo as convenções geralmente utilizadas.
A interface gráfica do programa GOP permite visualizar os perfis de modos ópticos (modo
Ex
→ componente de campo Ex e modo Ey
→ componente de campo Hx), para cada passo do
refinamento auto-adaptativo e para até os três primeiros modos guiados. A Fig. 13 mostra o
botão para escolha da opção de visualização do campo óptico. A Fig. 14 apresenta o campo
para escolha do modo óptico e o passo de refinamento auto-adaptativo (iteração) para os quais
serão apresentados os valores de campo. A Fig. 15 apresenta o perfil de campo óptico do
modo fundamental após o termino do processo de iteração.
Fig. 13 Botão para escolha da opção de apresentação do perfil de campo óptico.
D E

37. 30
Fig. 14 Campo para escolha do modo analisado e passo de iteração para apresentação gráfica de resultados.
Fig. 15 Perfil de campo óptico para o modo fundamental (
(
11 ).
As Figs 16a –16l apresentam os perfis de campo do modo óptico fundamental (
(
11 ) para cada
uma das doze iterações do processo de refinamento auto-adaptativo da malha de elementos
finitos. No primeiro passo de iteração, foi utilizada uma malha inicial de 15 elementos em
cada uma das duas camadas (cobertura e substrato). As Figs. 17a, 17b e 17c apresentam os
perfis de campo do segundo modo guiado, para o primeiro, sexto e décimo segundo passo do
processo de refinamento auto-adaptativo, respectivamente.
D E F G

38. 31
Fig. 16 Perfis de campo óptico para o modo fundamental de propagação em guia planar difuso (Ti:LiNbO3). As
Figs. 16a até 16l apresentam os perfis de campo calculados pelo programa GOP para cada um dos doze passos
do processo de refinamento auto-adaptativo da malha de elementos finitos, respectivamente. As amplitudes são
relativas e por este motivo o sinal do campo e seu valor máximo não são informações relevantes para
comparação dos resultados.
Fig. 17 Perfis de campo para o segundo modo óptico. As Figs. 16a, 16b e 16c apresentam os perfis de campo
para o primeiro, sexto e décimo segundo passo do processo de refinamento auto-adaptativo, respectivamente.
H I J K
L M N O
D E F

39. 32
Para o processo de refinamento auto-adaptativo da malha de elementos finitos, o erro relativo
é calculado em cada elemento finito e depende diretamente do comprimento e do gradiente do
campo óptico em seu interior. Esses valores são números relativos e sua amplitude só é
importante quando comparado ao erro dos outros elementos da mesma malha. No cálculo do
erro, o comprimento do elemento e o gradiente de campo no elemento são adequadamente
ponderados para que a malha seja refinada, principalmente nas regiões onde o gradiente de
campo varia mais acentuadamente. Os valores são utilizados para o cálculo da média dos
erros e do desvio padrão. De posse destes dados pode-se determinar quais elementos finitos
devem ser subdivididos para o refinamento da malha. As Figs. 18a e 18b apresentam os erros
relativos ao longo da malha de elementos finitos para o modo fundamental e segundo modo
guiado no último passo de iteração, respectivamente. Das Figs. 18a e 18b pode-se observar
que os máximos erros relativos para o modo fundamental são menores do que os erros para o
segundo modo. Isto ocorre devido à maior complexidade do perfil de campo do segundo
modo em comparação ao modo fundamental. Entretanto, ambos os modos foram considerados
no processo de refinamento e a malha final obtida é suficiente para que ambos os valores de
índice efetivo calculados tenham atingido o critério de estabilização (variação menor que
10−7
).
Fig. 18 Distribuição de erros relativos utilizados para no processo auto-adaptativo da malha de elementos finitos.
A Fig. 18a apresenta a distribuição de erros para o modo fundamental, enquanto a Fig. 18b apresenta os mesmos
dados para o segundo modo óptico guiado.
No processo auto-adaptativo, cada iteração resulta em um diferente valor de índice efetivo
(Q¡
). O critério de parada, para este processo, é a estabilização dos valores calculados para os
três possíveis modos guiados. Quando a variação de Q¡
, entre três passos consecutivos de
iteração, é inferior a 10−7
o cálculo é finalizado. As Figs. 19a e 19b mostram a evolução do
valor do índice efetivo para o modo fundamental e segundo modo guiado, respectivamente.
D E

40. 33
Fig. 19 Variação do valor do índice efetivo em função do passo de iteração do processo de refinamento auto-
adaptativo da malha de elementos finitos. A Fig. 19a e 19b apresentam os resultados para o modo fundamental e
segundo modo, respectivamente.
Quando um modo óptico apresenta valor de índice efetivo inferior ao valor do índice de
refração do substrato, o modo não é considerado um modo guiado. Neste caso grande parte do
campo óptico penetra a região do substrato e o modo é denominado modo de radiação do
substrato. O programa GOP automaticamente verifica se esta situação ocorre com algum dos
três modos ópticos calculados e indica esta condição ao usuário, quando este solicita a
visualização de seus resultados. A Fig. 20 apresenta a caixa de diálogo que alerta ao usuário
que o modo óptico solicitado não é um modo guiado e os resultados não serão apresentados.
Fig. 20 Caixa de diálogo indicando que o modo óptico solicitado não é um modo guiado. Neste caso, os
resultados não poderão ser visualizados.
O programa GOP armazena o tempo de processamento de cada passo de iteração. A variação
do tempo gasto em cada iteração pode ser visualizada na Fig. 21.
Fig. 21 Tempo de processamento utilizado para cada passo do processo de refinamento auto-adaptativo da
malha de elementos finitos.
D E

41. 34
,QIRUPDo}HV 6REUH R 3URFHVVR 'LIXVLYR
Esta janela (Fig. 22) pode ser visualizada a partir do menu principal acessando a opção
3URMHWR→3DUkPHWURV GR 3URFHVVR 'LIXVLYR 7L/L1E2