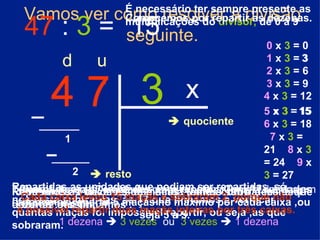
Este documento explica o conceito de divisão matemática. A divisão permite dividir um conjunto de elementos em partes iguais. Exemplifica dividindo 18 maçãs inicialmente uma a uma, depois duas a duas e três a três, mostrando que dividir seis a seis é mais rápido. Explica também como dividir 44 frutos em 3 caixas, primeiro dividindo as dezenas e depois as unidades restantes.