O documento aborda os princípios de modulação em comunicações, especificamente modulação em amplitude (AM), em frequência (FM) e em fase (PM). Ele discute como a modulação altera características da onda portadora para transmitir sinais, destacando vantagens como maior faixa de frequência e menor tamanho das antenas. Também são apresentadas fórmulas e conceitos relacionados às interferências em modulação de sinais.



![Modulação Analógica
Sc = Ac(t) cos(ω0t + Φ0)
Sc = Ac cos[ω(t).t + Φ0]
Modulação em Amplitude (AM):
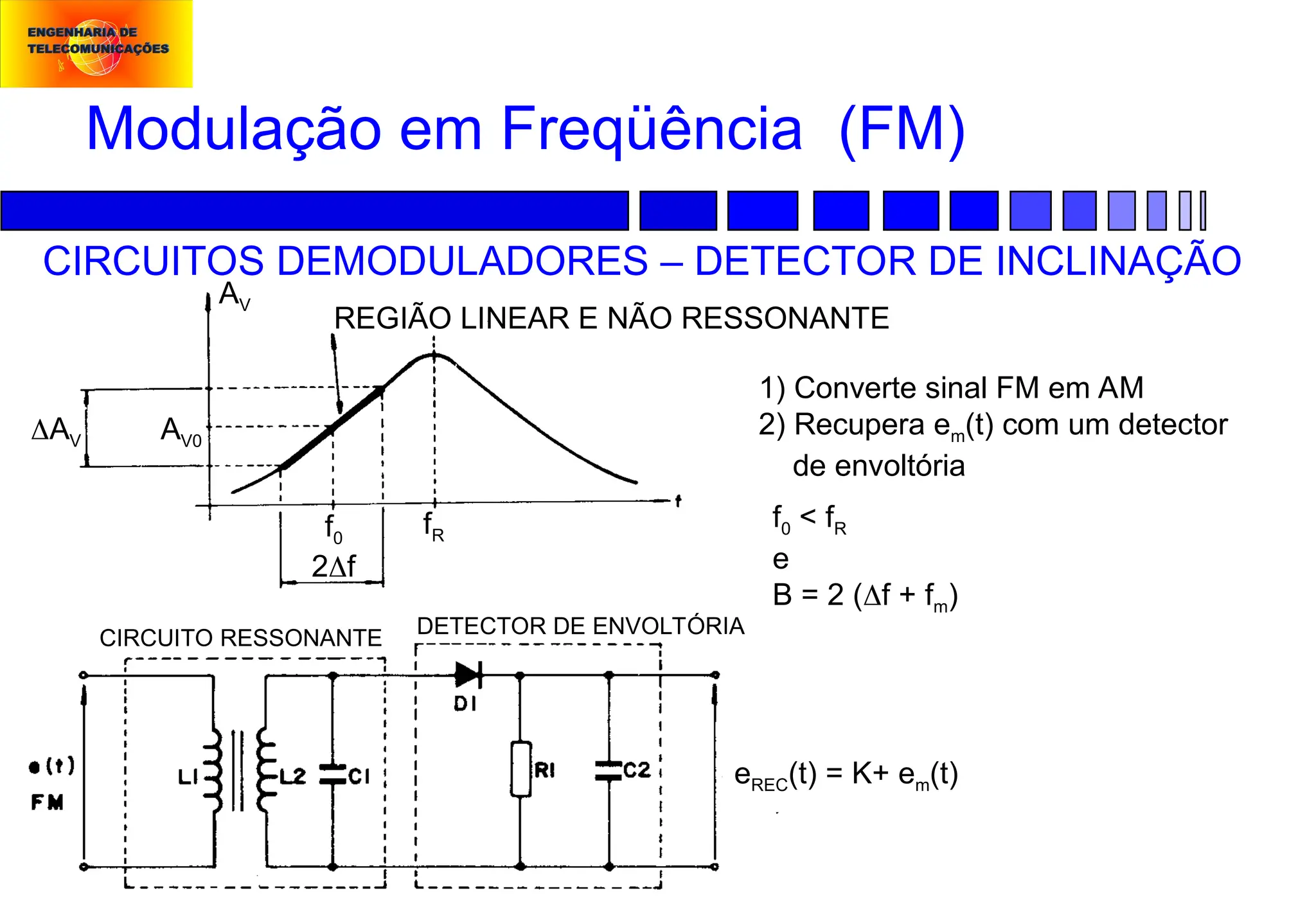
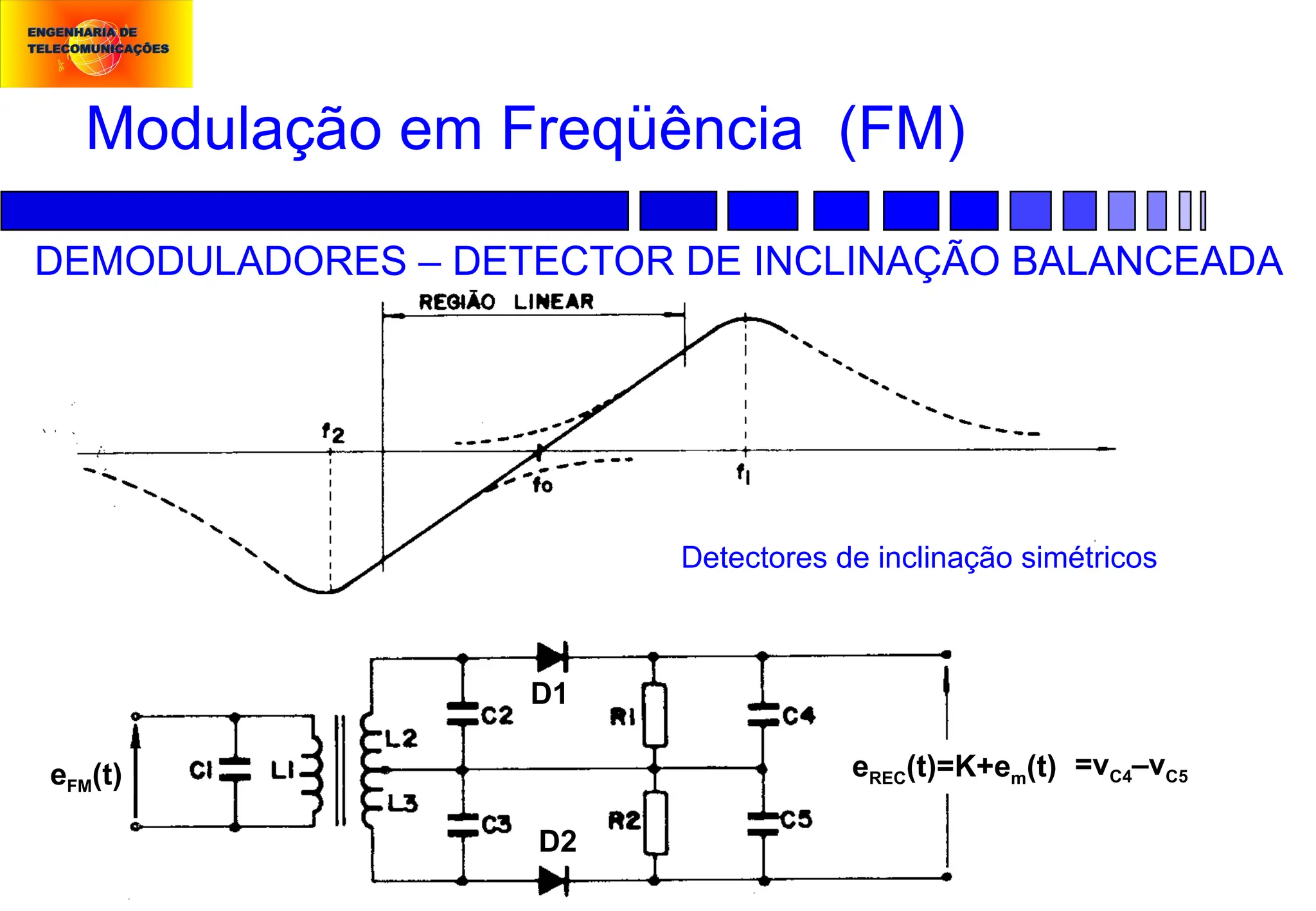
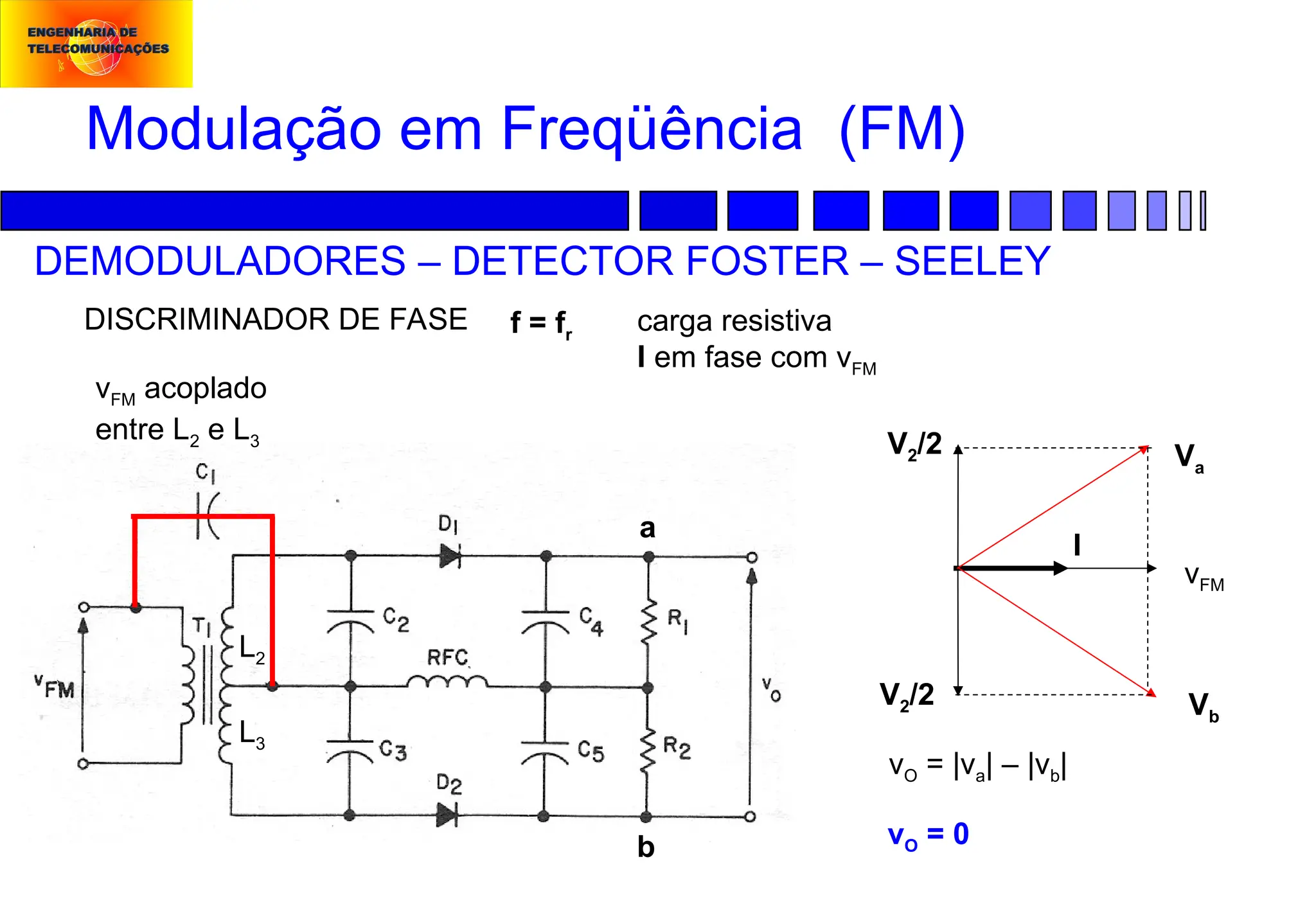
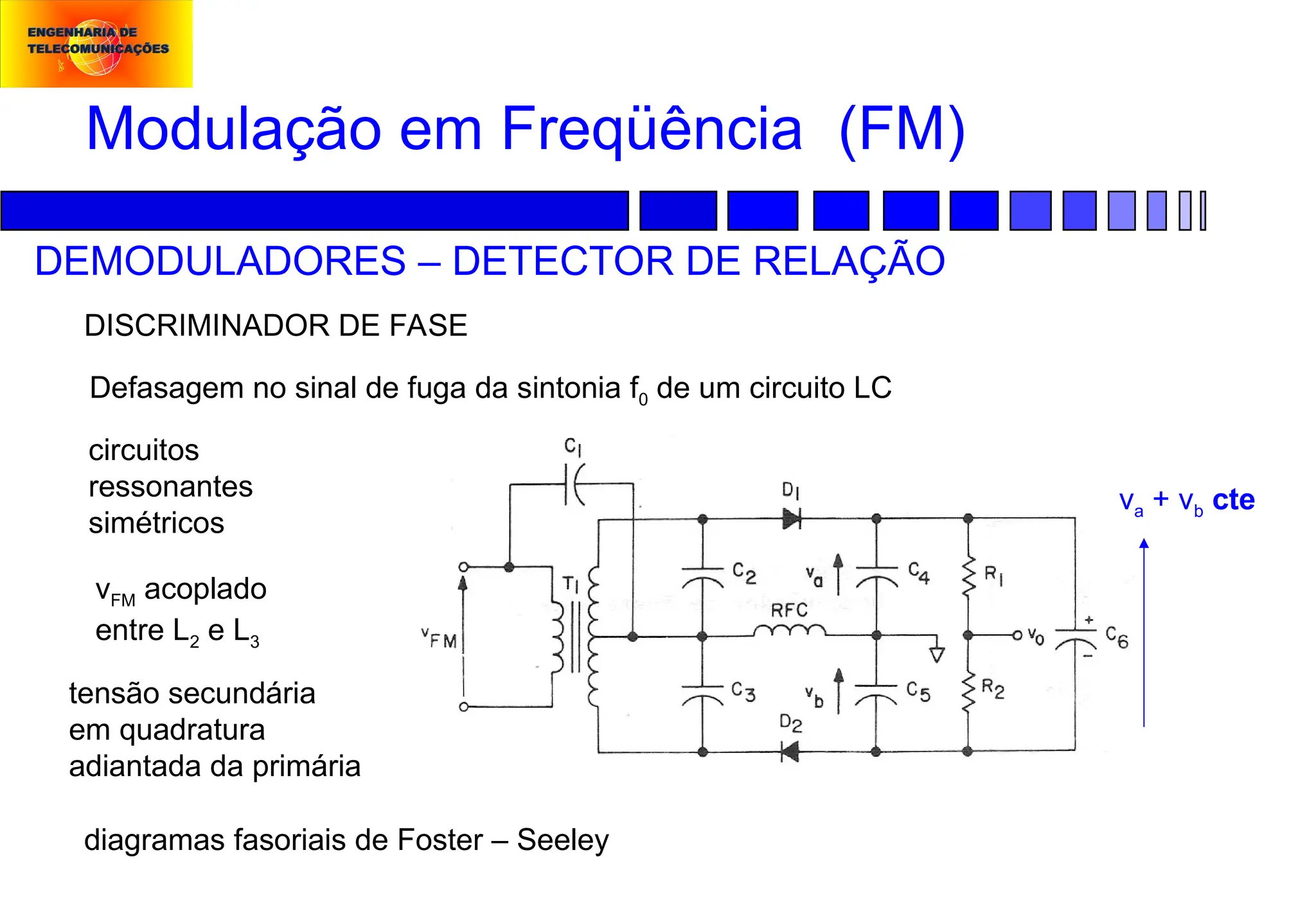
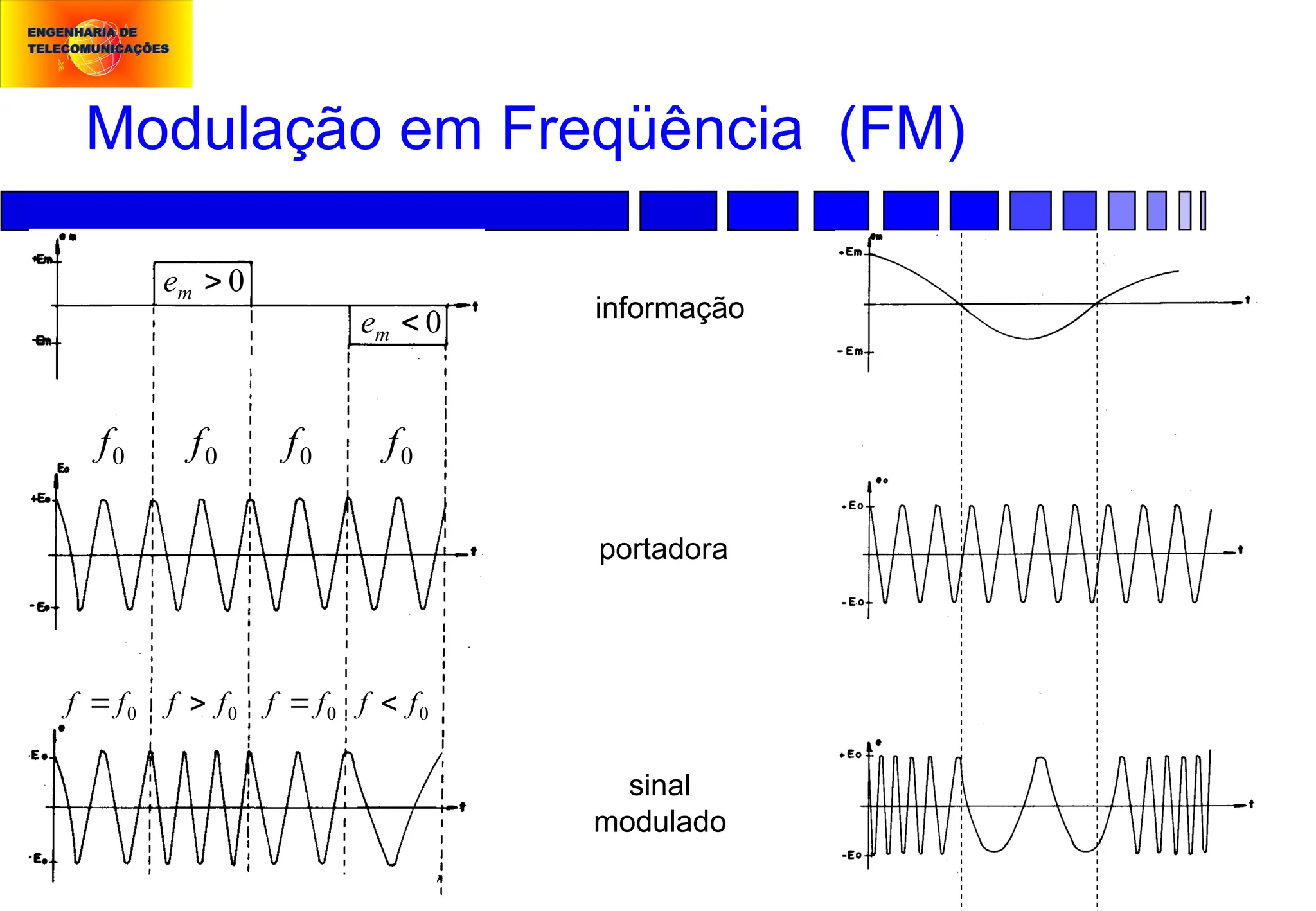
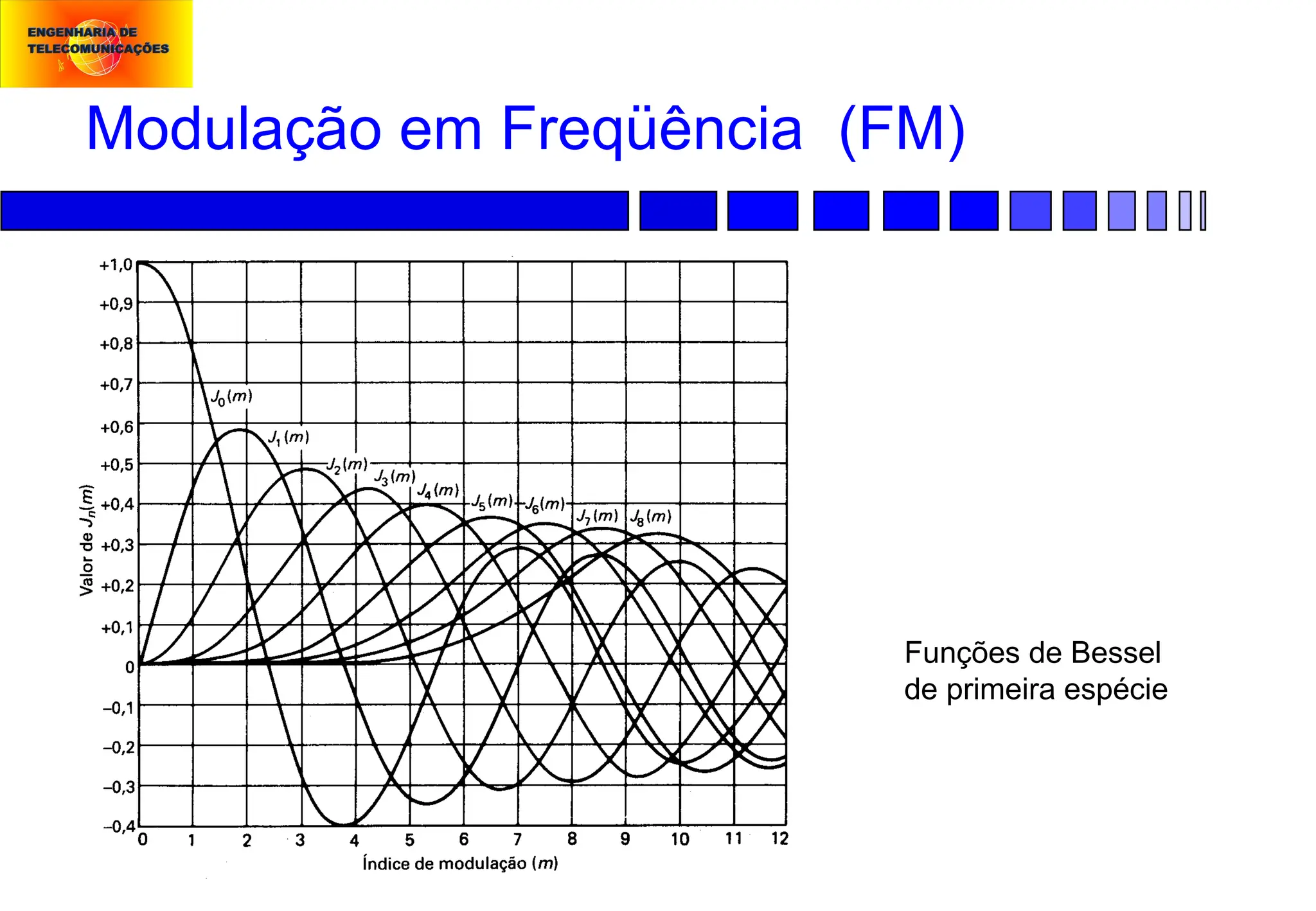
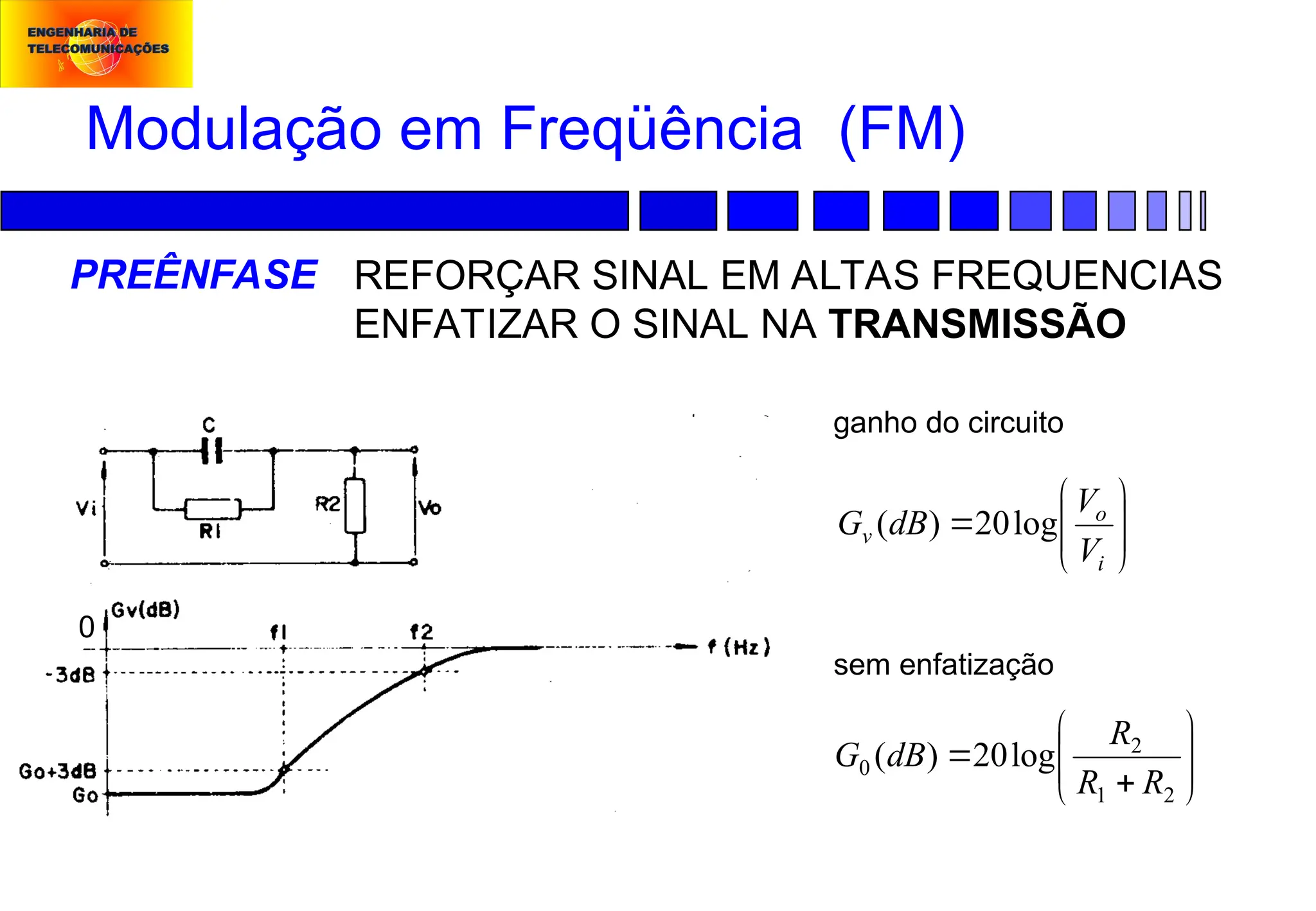
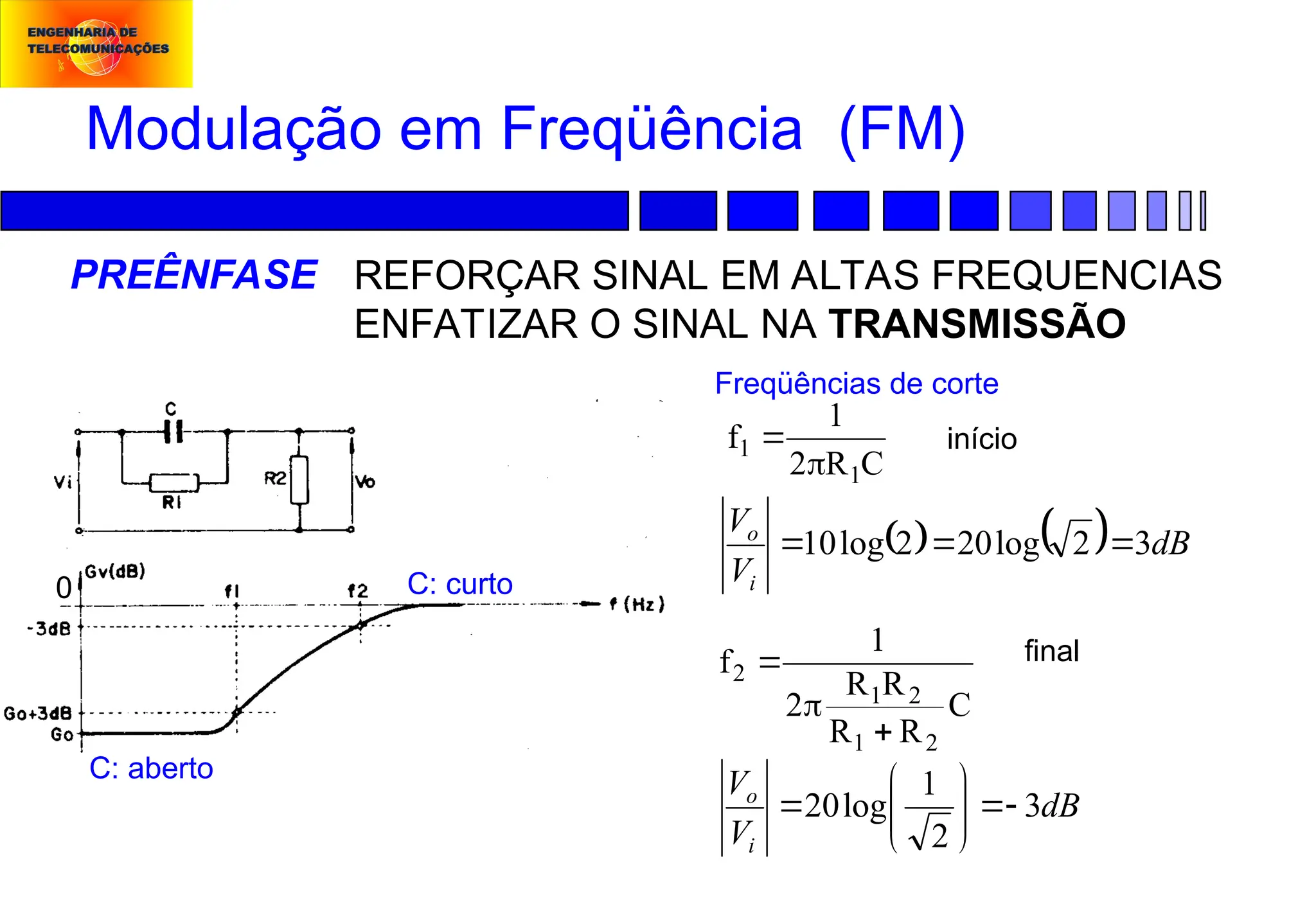
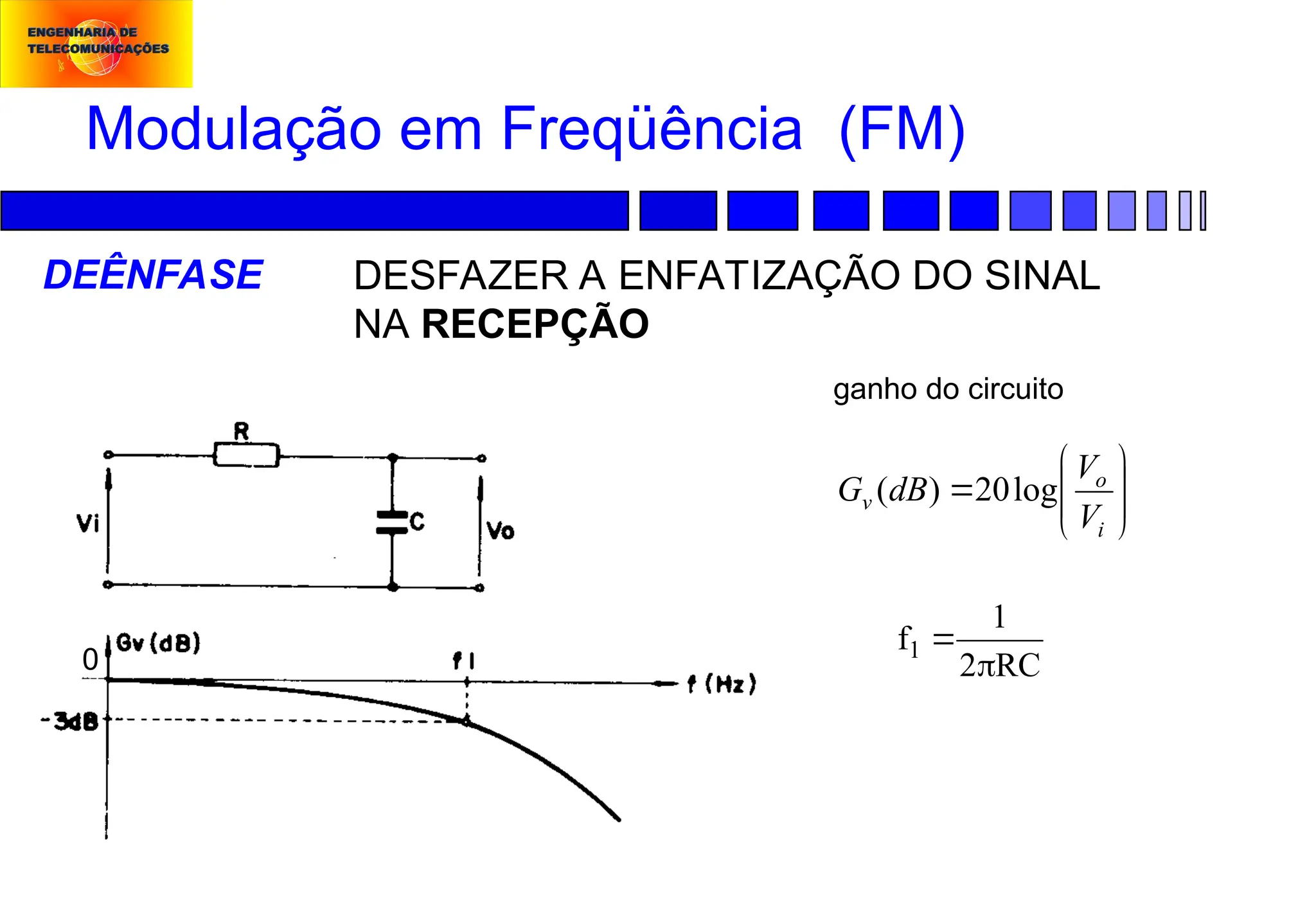
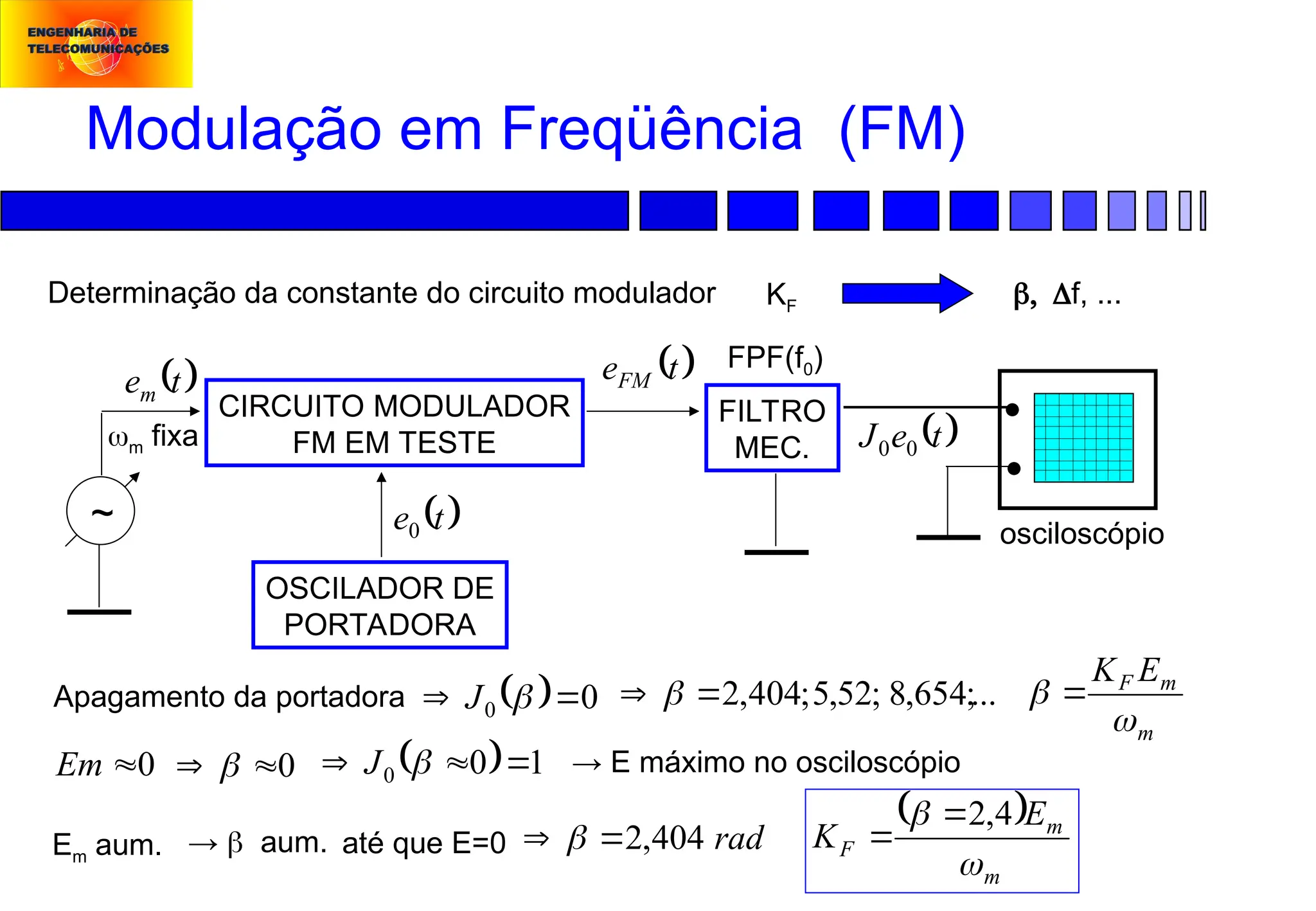
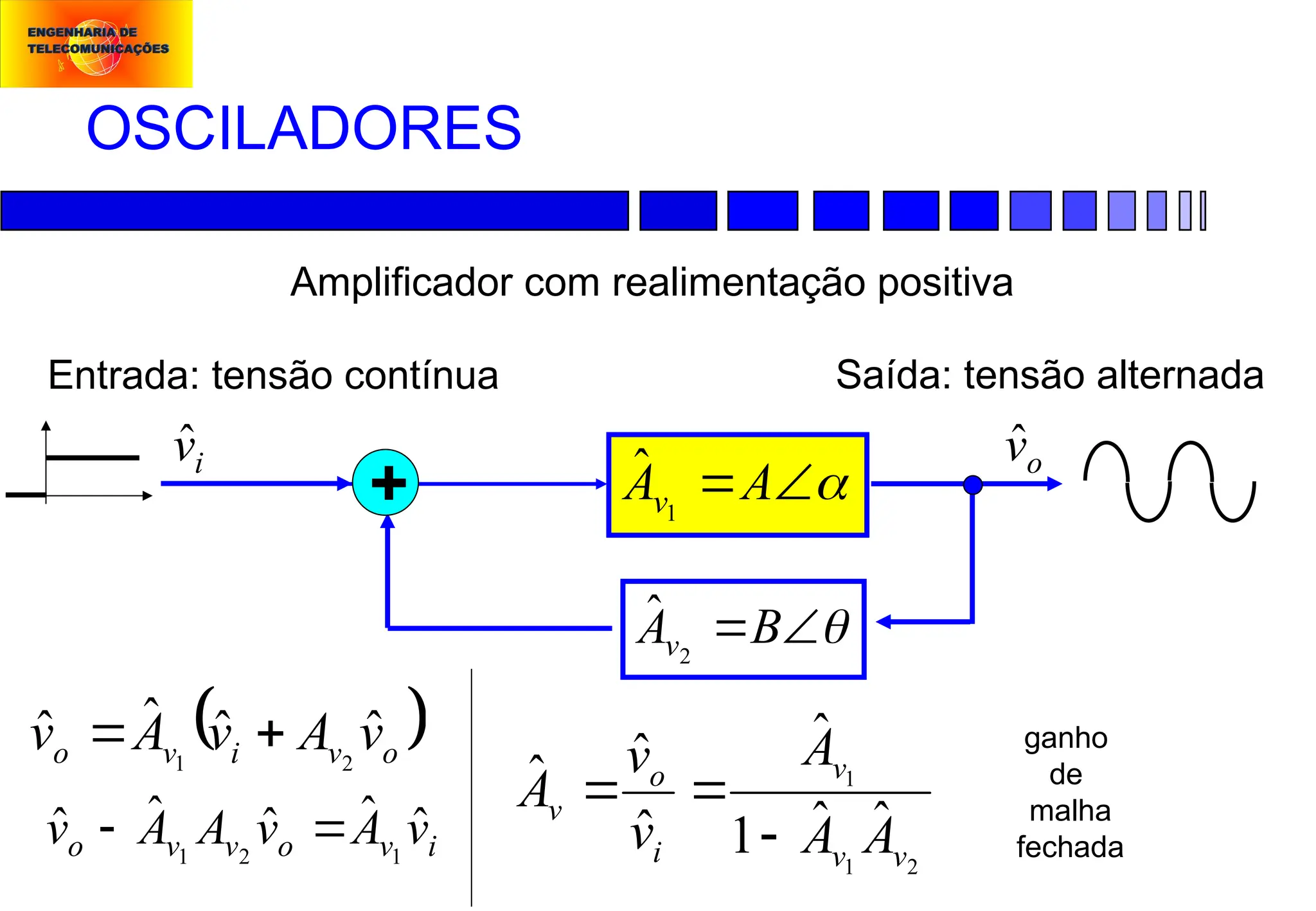
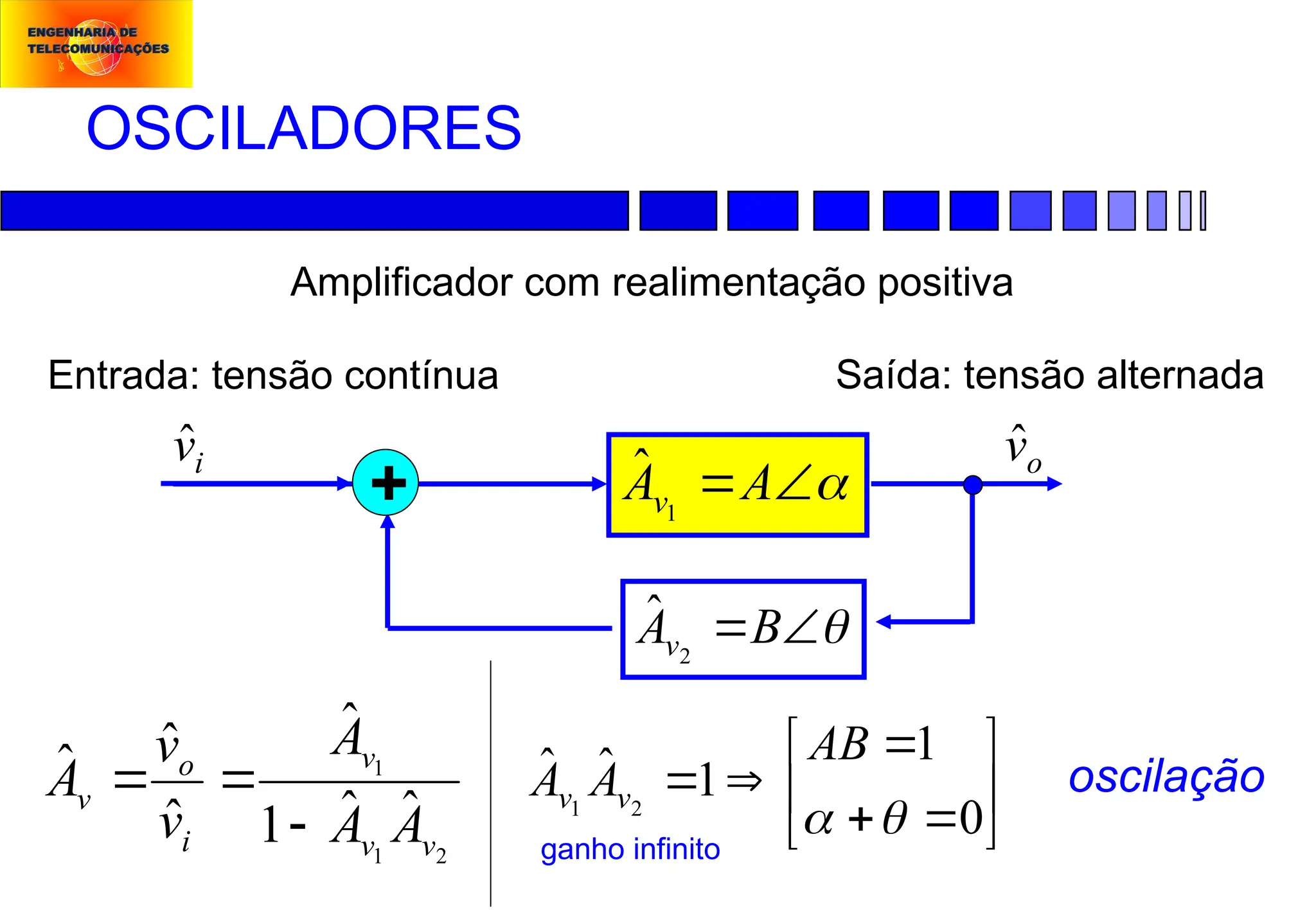
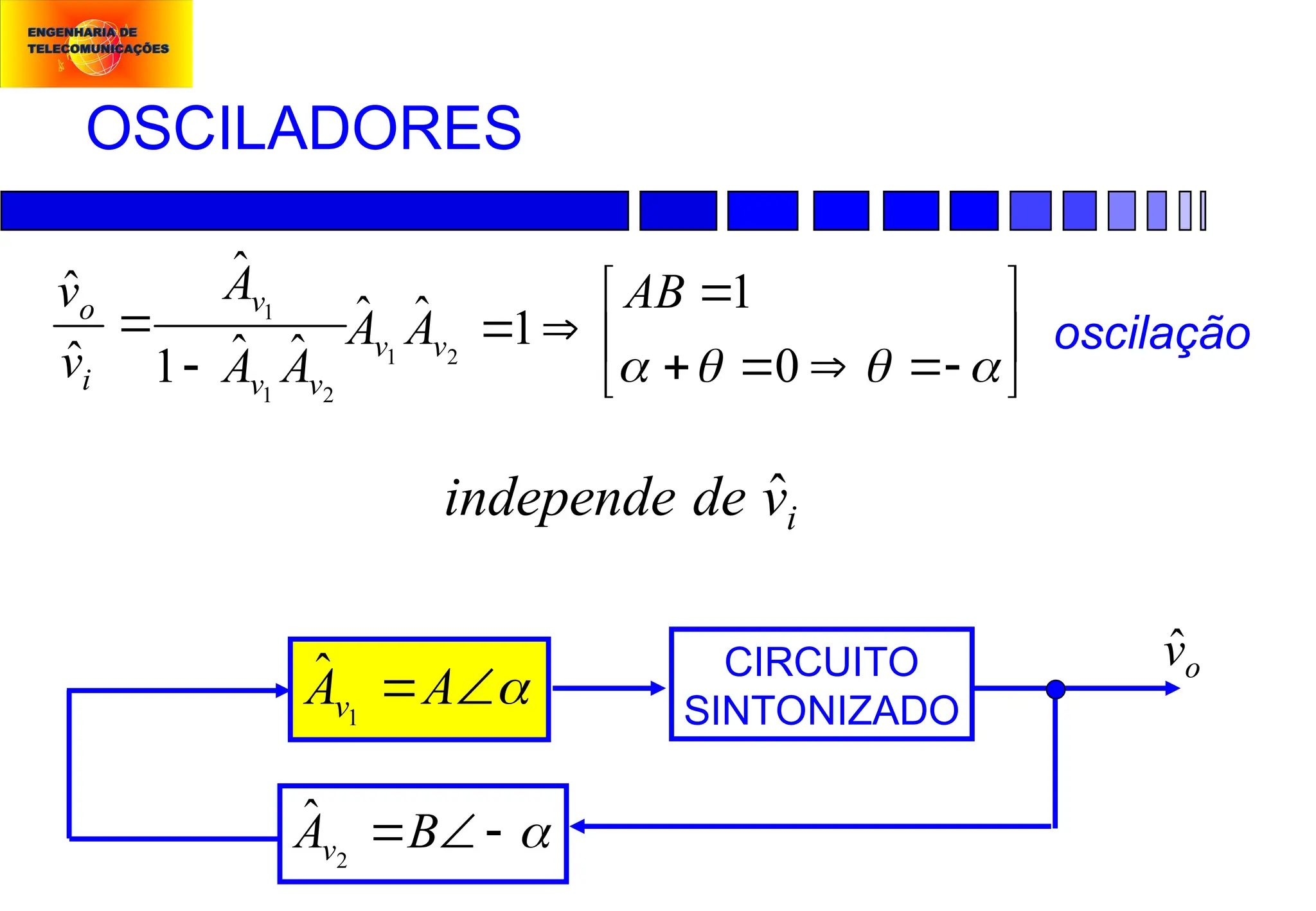
Modulação em Freqüência (FM):
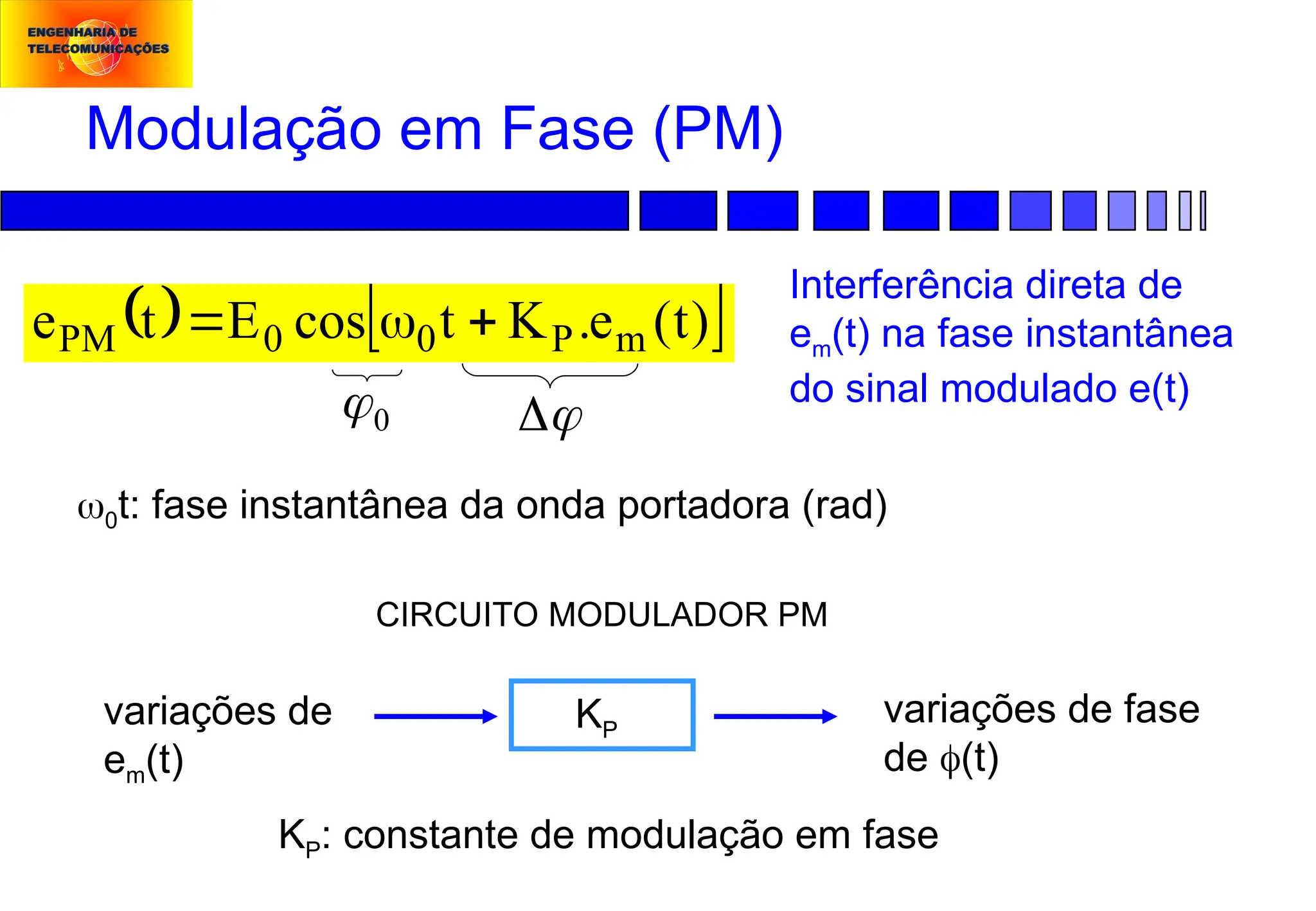
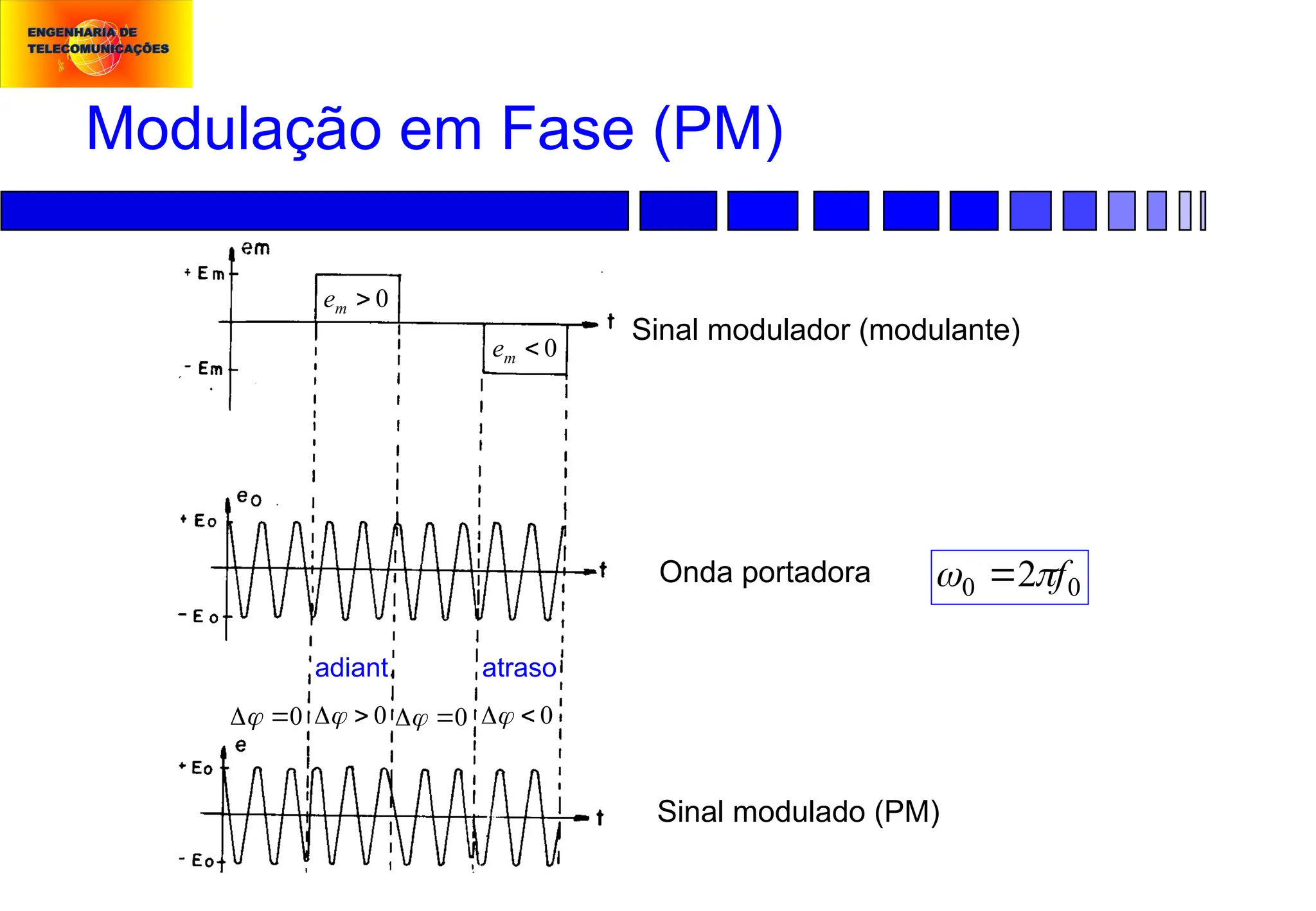
Modulação em Fase (PM):
Sc = Ac cos[ω0t + Φ(t)]
SINAL MODULANTE](https://image.slidesharecdn.com/pc10-240816025059-75f48e7f/75/pc-10-para-subir-por-encargo-en-internet-4-2048.jpg)



























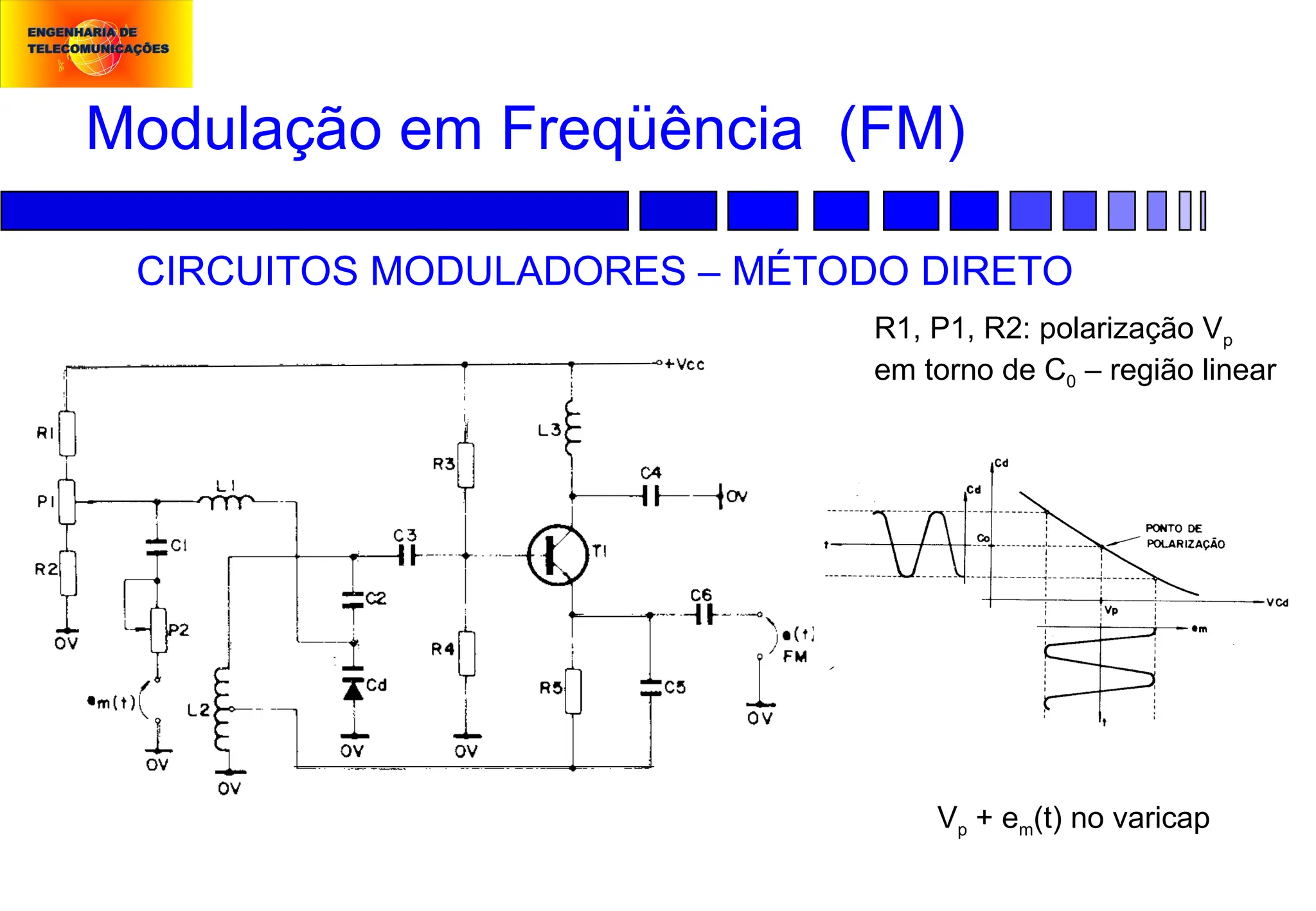







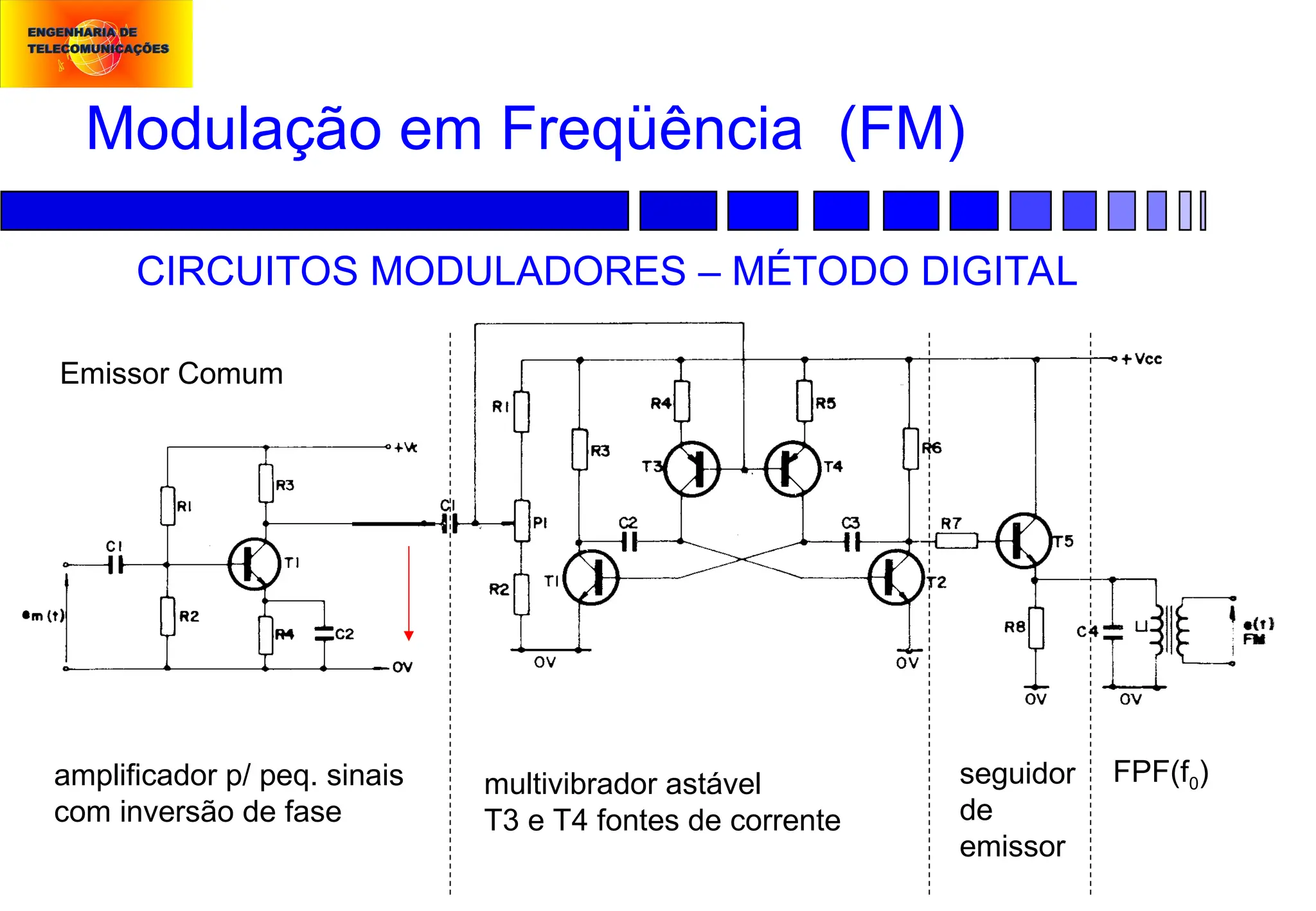
![Modulação em Freqüência (FM)
CIRCUITOS MODULADORES – MÉTODO DIGITAL
R4=R5=RE
T3 e T4 fontes de corrente
grande → IE ≈ IC = I
VCONT = VP + [ – em(t) ]
VP = polarização
VCC – VCONT = vEB + IRE
I
E
m
I
E
EB
P
CC
R
t
e
R
v
V
V
I
0
E
EB
m
P
CC IR
v
t
e
V
V
](https://image.slidesharecdn.com/pc10-240816025059-75f48e7f/75/pc-10-para-subir-por-encargo-en-internet-52-2048.jpg)