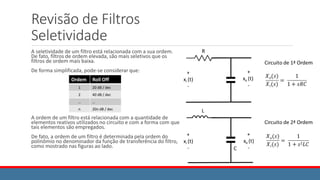
O documento aborda conceitos fundamentais das comunicações analógicas, incluindo a transformação de informação em sinal para transmissão e os diferentes tipos de comunicação (simplesx, semi-duplex e duplex). Ele explora os meios de transmissão, modulação em amplitude (AM), e técnicas de demodulação síncrona, destacando a importância de manter a sincronização entre transmissor e receptor. Também é discutida a modulação AM-DSB, que inclui a portadora no sinal transmitido, simplificando a recepção e permitindo uma melhor eficiência na transmissão.



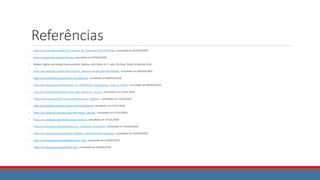
![Tipos de Modulação Analógica
Tipo Forma Funcional da Banda Base Forma Funcional do Sinal Modulado
AM A(t) = f [ x(t) ] xm(t) = A(t) cos [ ωct + θ0 ]
FM ω(t) = f [ x(t) ] xm(t) = A cos [ω(t) t + θ0 ]
PM θ(t) = f [ x(t) ] xm(t) = A cos [ωct + θ(t) ]](https://image.slidesharecdn.com/1-240930004611-f8d91517/85/1-Comunicacoes-Analogicas-v5-pdf-7-320.jpg)

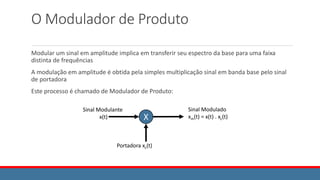
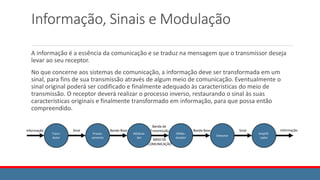
![O Modulador de Produto
Exemplo 1
Este exemplo ilustra o modulador de produto, usando uma
portadora do tipo senoidal:
f(t) = A cos ωmt
c(t) = B cos ωct
m(t) = A cos ωmt . B cos ωct
= AB cos ωmt . cos ωct
Lembrete:
cos (a+b) = cos a cos b – sen a sen b
cos (a-b) = cos a cos b + sen a sen b
cos a . cos b =
1
2
[ cos (a+b) + cos (a-b) ]
m(t) =
AB
2
[ cos (ωc + ωm)t + cos (ωc - ωm)t ]
Deve-se notar que o sinal resultante não possui nenhum
componente na frequência da portadora utilizada
𝜔
𝜔
𝜔
𝜔𝑚
𝜔𝑐 + 𝜔𝑚
𝜔𝑐 − 𝜔𝑚
𝜔𝑐
A
B
AB/2
𝜔
𝜔
𝜔
𝜔𝑚
−𝜔𝑚
𝜔𝑐 + 𝜔𝑚
𝜔𝑐 − 𝜔𝑚
−(𝜔𝑐 + 𝜔𝑚) −(𝜔𝑐 − 𝜔𝑚)
𝜔𝑐
−𝜔𝑐
A/2
B/2
AB/4](https://image.slidesharecdn.com/1-240930004611-f8d91517/85/1-Comunicacoes-Analogicas-v5-pdf-10-320.jpg)
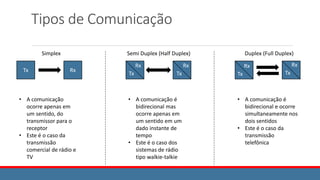
![O Modulador de Produto
Exemplo 2
Este exemplo ilustra o modulador de produto, usando uma
portadora do tipo senoidal, com um sinal modulante qualquer:
f(t) é um sinal modulante qualquer, com a banda base
mostrada
c(t) = cos ωct
m(t) = f(t) cos ωct
M(ω) =
1
2
[ F (ω - ωc) + F (ω + ωc ) ]
Tal como antes, o sinal resultante não possui nenhum
componente na frequência da portadora utilizada
𝜔
𝜔
𝜔
𝜔𝑚
𝜔𝑐 + 𝜔𝑚
𝜔𝑐 − 𝜔𝑚
𝜔𝑐](https://image.slidesharecdn.com/1-240930004611-f8d91517/85/1-Comunicacoes-Analogicas-v5-pdf-11-320.jpg)


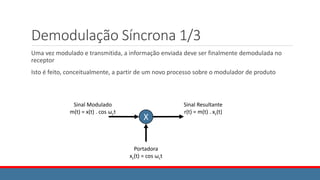
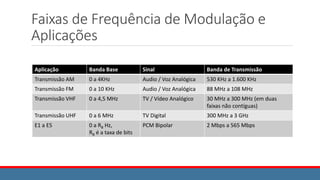
![Demodulação Síncrona 2/3
r(t) = m(t) . xc(t)
xc(t) = cos ωct
m(t) = f(t) . xc(t) = f(t) . cos ωct
r(t) = f(t) . xc(t) . xc(t)
= f(t) . cos ωct . cos ωct
= f(t) . cos2 ωct
Lembrete:
cos (2a) = cos2 a – sen2 a
1 = cos2 a + sen2 a
cos2 a =
1
2
[ 1 + cos 2a ]
r(t) = f(t) .
1
2
[ 1 + cos 2 ωct ]
=
1
2
[ f(t) + f(t) . cos 2 ωct ]
R(ω) =
1
2
F(ω) +
1
4
[ F(ω + 2ωc) + F(ω - 2ωc) ]
𝜔
𝜔
𝜔
𝜔𝑚
𝜔𝑐 + 𝜔𝑚
𝜔𝑐 − 𝜔𝑚
𝜔𝑐
2𝜔𝑐 + 𝜔𝑚
2𝜔𝑐 − 𝜔𝑚
𝜔𝑐 2𝜔𝑐
𝜔
𝜔𝑚
M(ω)
X(ω)
R(ω)
F(ω)](https://image.slidesharecdn.com/1-240930004611-f8d91517/85/1-Comunicacoes-Analogicas-v5-pdf-15-320.jpg)
![Demodulação Síncrona 2/3
r(t) = m(t) . xc(t)
xc(t) = cos ωct
m(t) = f(t) . xc(t) = f(t) . cos ωct
r(t) = f(t) . xc(t) . xc(t)
= f(t) . cos ωct . cos ωct
= f(t) . cos2 ωct
Lembrete:
cos (2a) = cos2 a – sen2 a
1 = cos2 a + sen2 a
cos2 a =
1
2
[ 1 + cos 2a ]
r(t) = f(t) .
1
2
[ 1 + cos 2 ωct ]
=
1
2
[ f(t) +) +
1
4
f(t) . cos 2 ωct ]
R(ω) =
1
2
F(ω [ F(ω + 2ωc) + F(ω - 2ωc) ]
𝜔
𝜔
𝜔
𝜔𝑚
𝜔𝑐 + 𝜔𝑚
𝜔𝑐 − 𝜔𝑚
𝜔𝑐
2𝜔𝑐 + 𝜔𝑚
2𝜔𝑐 − 𝜔𝑚
𝜔𝑐 2𝜔𝑐
𝜔
𝜔𝑚
M(ω)
X(ω)
R(ω)
F(ω)](https://image.slidesharecdn.com/1-240930004611-f8d91517/85/1-Comunicacoes-Analogicas-v5-pdf-16-320.jpg)
![Demodulação Síncrona 2/3
r(t) = m(t) . xc(t)
xc(t) = cos ωct
m(t) = f(t) . xc(t) = f(t) . cos ωct
r(t) = f(t) . xc(t) . xc(t)
= f(t) . cos ωct . cos ωct
= f(t) . cos2 ωct
Lembrete:
cos (2a) = cos2 a – sen2 a
1 = cos2 a + sen2 a
cos2 a =
1
2
[ 1 + cos 2a ]
r(t) = f(t) .
1
2
[ 1 + cos 2 ωct ]
=
1
2
[ f(t) +) +
1
4
f(t) . cos 2 ωct ]
R(ω) =
1
2
F(ω [ F(ω + 2ωc) + F(ω - 2ωc) ]
𝜔
𝜔
𝜔
𝜔𝑚
𝜔𝑐 + 𝜔𝑚
𝜔𝑐 − 𝜔𝑚
𝜔𝑐
2𝜔𝑐 + 𝜔𝑚
2𝜔𝑐 − 𝜔𝑚
𝜔𝑐 2𝜔𝑐
𝜔
𝜔𝑚
M(ω)
X(ω)
R(ω)
F(ω)](https://image.slidesharecdn.com/1-240930004611-f8d91517/85/1-Comunicacoes-Analogicas-v5-pdf-17-320.jpg)
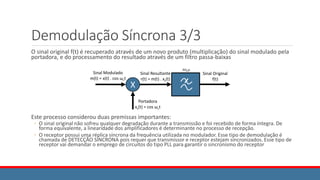
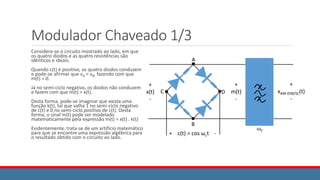
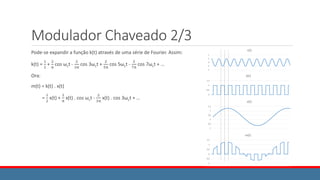

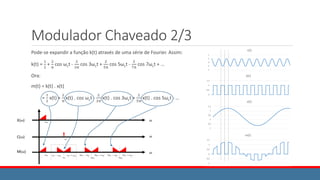



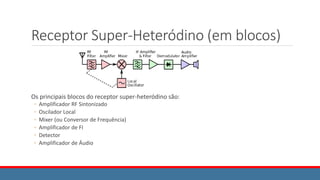
![Características do Modulador
Como pode ser visto, da figura mostrada:
xAM(t) = x(t) . cos ωct + A . cos ωct
= [ x(t) + A ] cos ωct
Deve-se notar que o componente [ x(t) + A ] da forma funcional do sinal AM acaba se
constituindo como uma amplitude (variável) da portadora.
Assim, o sinal da portadora apresentará uma amplitude que segue o “contorno” do
componente [ x(t) + A ].
Uma vez que a frequência da portadora é, normalmente, muito maior que a largura
de banda da banda base, vai-se notar um efeito de “espelhamento” do sinal
modulante (o componente [ x(t) + A ] ), em torno do eixo horizontal.
É fácil perceber que o sinal em banda base surge como uma “envoltória” ou
“envelope” do sinal da portadora. Nestes casos, a recuperação do sinal em banda
base pode ser feito através de uma simples retificação e filtragem do sinal modulado.
Este processo é chamado de “detector de envoltória” ou “detector de envelope”.
X
𝑥 𝑡
cos 𝜔𝐶𝑡
𝑥𝐴𝑀 𝑡
+
A](https://image.slidesharecdn.com/1-240930004611-f8d91517/85/1-Comunicacoes-Analogicas-v5-pdf-26-320.jpg)
![Índice de Modulação AM
Como discutido, deve-se considerar o termo [ x(t) + A ] no sinal modulado, como a
amplitude da portadora.
Desta forma, é importante garantir que esta expressão seja positiva para qualquer
instante de tempo. Isto é garantido fazendo com que o valor de A seja suficientemente
elevado. Assim:
x(t) + A ≥ 0
A ≥ - x(t) |MIN , para qualquer instante de tempo
μ =
− x(t) |MIN
𝐴
≤ 1, índice de modulação AM
Considerando que o valor mínimo de x(t) já será negativo, o índice de modulação AM
será sempre um valor positivo e menor que 1.
Se x(t) + A < 0, ocorrerá a chamada sobre-modulação. Neste caso, haverá um período
de tempo em que a “amplitude” da portadora será negativa. Durante este período,
haverá uma inversão de fase do sinal da portadora, gerando uma distorção da
envoltória. Assim, a recuperação do sinal não poderá ser feita de forma simplificada,
através de um “detector de envoltória”.](https://image.slidesharecdn.com/1-240930004611-f8d91517/85/1-Comunicacoes-Analogicas-v5-pdf-27-320.jpg)
![Exemplo
Supondo que a figura mostrada ao lado foi produzida a partir de um simples
tom x(t) = B . cos ωmt como sinal modulante da portadora A . cos ωct, calcule o
índice de modulação AM.
Resposta:
Sabe-se que:
◦ xAM(t) = [ x(t) + A ] cos ωct
Desta forma, pode-se inferir que o valor máximo do sinal modulado é, na
verdade, a soma dos picos do sinal modulante e da portadora. Por outro lado, o
valor mínimo do sinal modulado é exatamente a subtração das duas
amplitudes. Assim:
A + B = 10 A = 7,5
A – B = 5 B = 2,5
Então:
μ =
𝐵
𝐴
=
2,5
7,5
=
1
3
= 33,3%
AM-DSB
-15
-10
-5
0
5
10
15](https://image.slidesharecdn.com/1-240930004611-f8d91517/85/1-Comunicacoes-Analogicas-v5-pdf-28-320.jpg)
![Percentual de Potência na Banda Lateral
Como discutido, o sinal modulado possui duas parcelas: a modulação AM-DSB e a portadora
xAM(t) = x(t) . cos ωct + A . cos ωct
Do ponto de vista da potência transmitida, têm-se:
PTOTAL = PAM + PC
PC =
1
𝑇
0
𝑇
𝐴2
𝑐𝑜𝑠2
𝜔𝑐t dt =
1
2
𝐴2
PAM =
1
𝑇
0
𝑇
𝑥2
𝑡 𝑐𝑜𝑠2
𝜔𝑐t dt =
1
2
𝑥2
(t)
PTOTAL =
1
2
[ A2
+ 𝑥2
(t) ]
Assim, o percentual de potência na banda lateral, ou seja, a parcela de potência efetivamente empregada na transmissão da informação,
é dado por:
ƞ =
PAM
PTOTAL
=
1
2
𝑥2(t)
1
2
[ A2+ 𝑥2(t) ]
=
𝑥2(t)
A2+ 𝑥2(t)
x 100%](https://image.slidesharecdn.com/1-240930004611-f8d91517/85/1-Comunicacoes-Analogicas-v5-pdf-29-320.jpg)

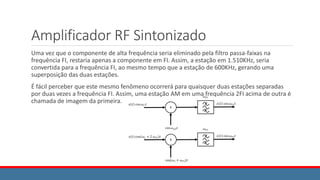
![Modulador AM-DSB Chaveado
Do circuito ao lado tem-se que:
xA(t) = x(t) + A cos ωct
Tal como antes, vai-se usar o artifício matemático de usar
uma função k(t), tal como descrita na figura. Assim:
xB(t) = xA(t) . k(t)
= [x(t) + A cos ωct ] [
1
2
+
2
π
cos ωct -
2
3π
cos 3ωct + … ]
=
1
2
x(t) +
1
2
A cos ωct +
2
π
x(t) cos ωct +
2
π
A cos2 ωct + …
Expansão de k(t) em Fourier:
k(t) =
1
2
+
2
π
cos ωct -
2
3π
cos 3ωct +
2
5π
cos 5ωct - …](https://image.slidesharecdn.com/1-240930004611-f8d91517/85/1-Comunicacoes-Analogicas-v5-pdf-31-320.jpg)
![Modulador AM-DSB Chaveado
Do circuito ao lado tem-se que:
xA(t) = x(t) + A cos ωct
Tal como antes, vai-se usar o artifício matemático de usar
uma função k(t), tal como descrita na figura. Assim:
xB(t) = xA(t) . k(t)
= [x(t) + A cos ωct ] [
1
2
+
2
π
cos ωct -
2
3π
cos 3ωct + … ]
=
1
2
x(t) +
1
2
A cos ωct +
2
π
x(t) cos ωct +
2
π
A cos2 ωct + …
Expansão de k(t) em Fourier:
k(t) =
1
2
+
2
π
cos ωct -
2
3π
cos 3ωct +
2
5π
cos 5ωct - …](https://image.slidesharecdn.com/1-240930004611-f8d91517/85/1-Comunicacoes-Analogicas-v5-pdf-32-320.jpg)
![Modulador AM-DSB Chaveado (cont)
[SLIDE OPCIONAL]
Desenvolvimento com mais termos:
xB(t) = xA(t) . k(t)
= [x(t) + A cos ωct ] [
1
2
+
2
π
cos ωct -
2
3π
cos 3ωct +
2
5π
cos 5ωct - … … ]
=
1
2
x(t) +
1
2
A cos ωct +
2
π
x(t) cos ωct +
2
π
A cos2 ωct -
2
3π
x(t)cos 3ωct -
2
3π
A cos ωct cos 3ωct + …
=
1
2
x(t) +
1
2
A cos ωct +
2
π
x(t) cos ωct +
1
π
A [1+cos 2ωct] -
2
3π
x(t)cos 3ωct -
2
3π
A cos ωct cos 3ωct + …
=
1
π
A +
1
2
x(t) +
1
2
A cos ωct +
2
π
x(t) cos ωct +
1
π
A cos 2ωct -
2
3π
x(t)cos 3ωct -
2
3π
A cos ωct cos 3ωct + …](https://image.slidesharecdn.com/1-240930004611-f8d91517/85/1-Comunicacoes-Analogicas-v5-pdf-33-320.jpg)



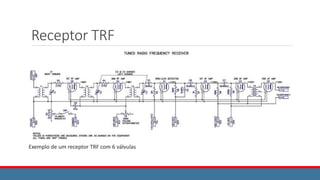

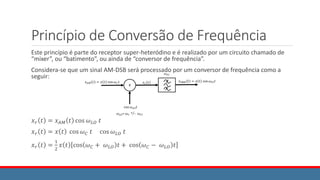
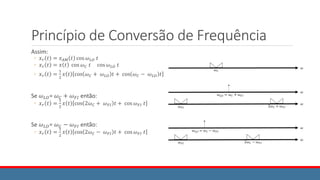













![Modulação e Demodulação QAM
O sinal na saída do modulador é dado por:
xQAM(t) = x1(t) cos ωct + x2(t) sen ωct
Este sinal é transmitido e percebido no receptor. O sinal intermediário
resultante é:
w1(t) = xQAM(t) cos ωct
= [x1(t) cos ωct + x2(t) sen ωct] cos ωct
= x1(t) cos2 ωct + x2(t) sen ωct cos ωct
=
1
2
[ x1(t) ( 1 + cos 2ωct ) + x2(t) sen 2ωct ]
=
1
2
[ x1(t) + x1(t) cos 2ωct + x2(t) sen 2ωct ]
Lembrete:
sen a cos a =
1
2
sen 2a
cos2 a =
1
2
( 1 + cos 2a )](https://image.slidesharecdn.com/1-240930004611-f8d91517/85/1-Comunicacoes-Analogicas-v5-pdf-56-320.jpg)
![Modulação e Demodulação QAM
O sinal na saída do modulador é dado por:
xQAM(t) = x1(t) cos ωct + x2(t) sen ωct
Este sinal é transmitido e percebido no receptor. O sinal intermediário
resultante é:
w1(t) = xQAM(t) cos ωct
= [x1(t) cos ωct + x2(t) sen ωct] cos ωct
= x1(t) cos2 ωct + x2(t) sen ωct cos ωct
=
1
2
[ x1(t) ( 1 + cos 2ωct ) + x2(t) sen 2ωct ]
=
1
2
[ x1(t) + x1(t) cos 2ωct + x2(t) sen 2ωct ]
Após o processamento pelo filtro passa-baixas tem-se: y1(t) =
1
2
x1(t)
De forma similar, tem-se que: y2(t) =
1
2
x2(t)
Lembrete:
sen a cos a =
1
2
sen 2a
cos2 a =
1
2
( 1 + cos 2a )
Banda Base](https://image.slidesharecdn.com/1-240930004611-f8d91517/85/1-Comunicacoes-Analogicas-v5-pdf-57-320.jpg)
![Interferência de Canal
No esquema mostrado, os dois sinais x1 e x2 são recuperados sem distorção. Isto se deveu à detecção coerente no
receptor. Para isso, foi necessário dispor, no receptor, de uma cópia exata da portadora utilizada no modulador. Uma
eventual falha no sincronismo do receptor pode levar a uma distorção chamada de INTERFERÊNCIA DE CANAL. Como
exemplo, considera-se que xc(t) = cos (ωct + θ). Nesse caso:
w1(t) = [x1(t) cos ωct + x2(t) sen ωct] cos (ωct + θ)
= x1(t) cos ωct cos (ωct + θ) + x2(t) sen ωct cos (ωct + θ)
= …
=
1
2
x1(t) cos θ -
1
2
x2(t) sen θ +
1
2
x1(t) cos (2ωct + θ) +
1
2
x2(t) sen (2ωct + θ)
Após a filtragem tem-se que:
y1(t) =
1
2
x1(t) cos θ -
1
2
x2(t) sen θ
Como pode ser visto, o canal 2 interfere na saída do canal 1. Como os dois termos estão em banda base não há como
filtrá-lo. Dependendo do valor de θ, o componente do canal 1 pode ser completamente mascarado (se θ = 90o). Este
processo foi usado como técnica de scrambling / jamming em sistemas de TV a Cabo analógicos.](https://image.slidesharecdn.com/1-240930004611-f8d91517/85/1-Comunicacoes-Analogicas-v5-pdf-58-320.jpg)