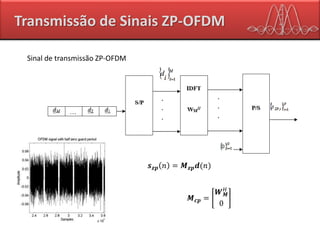
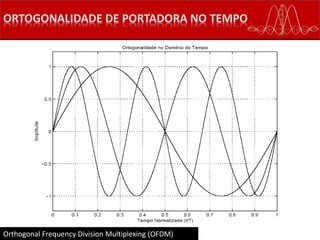
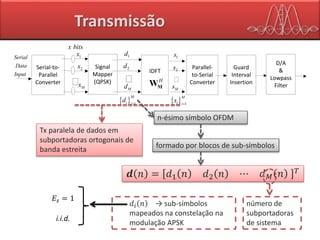
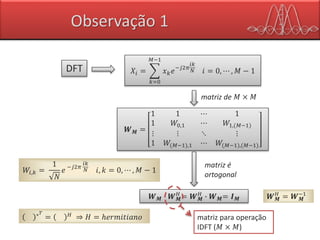
O documento descreve as principais características de sistemas de transmissão de dados por OFDM (Orthogonal Frequency Division Multiplexing). O OFDM divide o canal de transmissão em várias subportadoras ortogonais para transmitir dados em paralelo, aumentando a taxa de dados e a robustez ao ruído e interferências. Sistemas como Blu-ray, HD DVD e DVD usam diferentes taxas de dados e formatos de vídeo com OFDM.















![1
1
1
i
i
d
é ù
ê ú
ê ú
ê ú
ê ú= ê ú
ê ú
ê ú
ê ú-ê úë û
M
0 10 20 30 40 50 60 70
-0.2
-0.15
-0.1
-0.05
0
0.05
0.1
0.15
0.2
[ ]-0.09, -0.003-0.096i, , 0.01+ 0.247i, -0.035-0.0472is = L
Signal
Mapper
(QPSK)
IDFT
Parallel-
to-Serial
Converter
Guard
Interval
Insertion
Serial-to-
Parallel
Converter
2d
Md
Serial
Data
Input
1s
2s
Ms
x bits
D/A
&
Lowpass
Filter
1x 1d
2x
Mx
H
MW
1
M
i i
d 1
M
i i
s
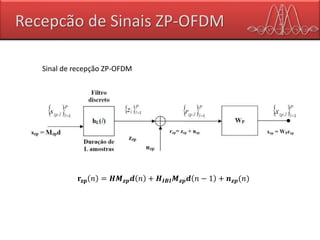
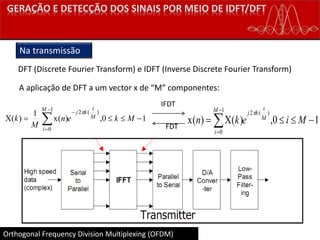
𝒔 = 𝑾 𝑴
𝐻
𝒅
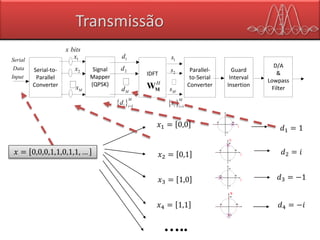
Transmissão](https://image.slidesharecdn.com/ofdm-final-160627223414/85/Ofdm-29-320.jpg)
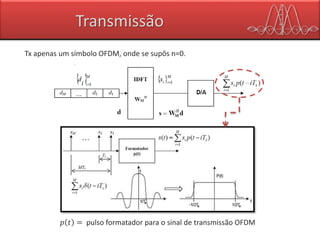
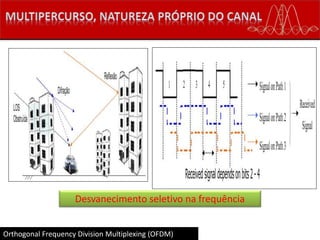
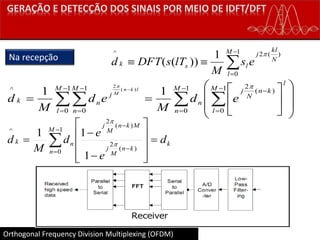
![Recepção
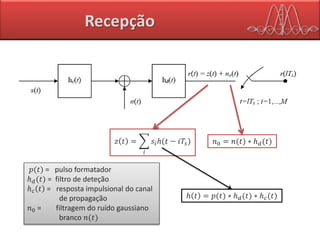
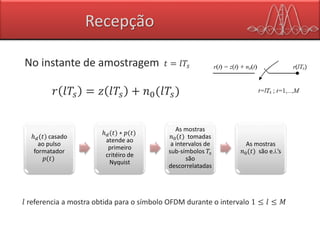
Para um instante 𝑛 (um único símbolo OFDM) o sinal que chega ao receptor, é:
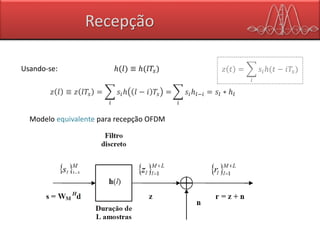
𝒛 𝑛 = 𝑯𝒔 𝑛 = 𝑯𝑾 𝑴
𝐻
𝒅 𝑛
𝑯 = matriz de convolução discreta para o canal 𝒉(𝑙)
𝑯 é matriz Toeplitz 𝑀 × 𝑀 (Matriz de diagonais contantes) cuja primeira coluna é:
[ℎ0 ⋯ ℎ 𝐿−1 01 0 𝑀−𝐿] 𝑇
O sinal de observação 𝒓 𝑛
𝒓 𝑛 = 𝒛 𝑛 + 𝒏(𝑛)
𝒏 𝑛 é vetor ruído gaussiano, média nula e matriz covariância 𝑲 𝒏 = 𝜎2 𝑰](https://image.slidesharecdn.com/ofdm-final-160627223414/85/Ofdm-34-320.jpg)
![DATA CP
CP
CP
CP
CP
1
1
1
i
i
d
é ù
ê ú
ê ú
ê ú
ê ú= ê ú
ê ú
ê ú
ê ú-ê úë û
M
0 10 20 30 40 50 60 70
-0.2
-0.15
-0.1
-0.05
0
0.05
0.1
0.15
0.2
[ ]-0.09, -0.003-0.096i, , 0.01+ 0.247i, -0.035-0.0472is = L
0 10 20 30 40 50 60 70 80
-0.2
-0.15
-0.1
-0.05
0
0.05
0.1
0.15
0.2
0 10 20 30 40 50 60 70 80
-0.2
-0.15
-0.1
-0.05
0
0.05
0.1
0.15
0.2
Signal
Mapper
(QPSK)
IDFT
Parallel-
to-Serial
Converter
Guard
Interval
Insertion
Serial-to-
Parallel
Converter
2d
Md
Serial
Data
Input
1s
2s
Ms
x bits
D/A
&
Lowpass
Filter
1x 1d
2x
Mx
H
MW
1
M
i i
d 1
M
i i
s
Transmissão de Sinais CP-OFDM](https://image.slidesharecdn.com/ofdm-final-160627223414/85/Ofdm-35-320.jpg)
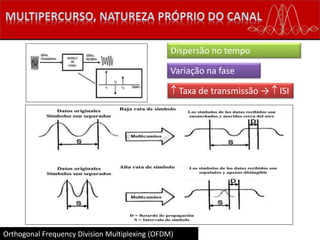
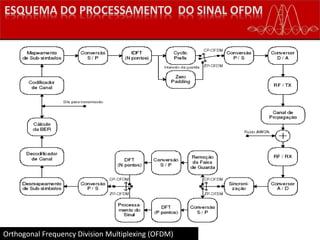
![Recepção de Sinais CP-OFDM
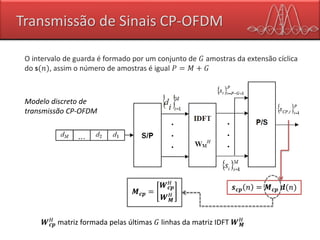
Considerando 𝒉 𝑳 = [ℎ0 ℎ1 ⋯ ℎ 𝐿−1] 𝑇
a
resposta impulsional do canal de
comprimento 𝐿 e 𝒏 𝒄𝒑 𝑛 um vetor de ruído
na recepção.
𝑀 > 𝐺 ≥ 𝐿 − 1](https://image.slidesharecdn.com/ofdm-final-160627223414/85/Ofdm-37-320.jpg)
![Recepcão de Sinais CP-OFDM
• A n-ésima observação de dimensão Px1, pode ser:
𝒓 𝒄𝒑 𝑛 = 𝑯𝑴 𝒄𝒑 𝒅 𝑛 + 𝑯𝒊𝒃𝒊 𝑴 𝒄𝒑 𝒅 𝑛 − 1 + 𝒏 𝒄𝒑(𝑛)
• 𝑯 = matriz Toeplitz 𝑃 × 𝑃 cuja primeira coluna é dada
por: [ℎ0 ⋯ ℎ 𝐿−1 01 0 𝑃−𝐿] 𝑇
• 𝑯𝒊𝒃𝒊 = matriz Troeplitz triangular superior 𝑃 × 𝑃 ,
representa a incidencia de IBI (interferencia inter blocos) e
sua primeira linha é dada por
𝑯𝒊𝒃𝒊 = [01 ⋯ 0 𝑃−𝐿+1 ℎ 𝐿−1 ⋯ ℎ1]](https://image.slidesharecdn.com/ofdm-final-160627223414/85/Ofdm-38-320.jpg)

![Recepcão de Sinais CP-OFDM
• O termo 𝑪𝒊𝒓𝒄 𝒉 representa a matriz circulante, cuja primeira coluna é
ℎ = [ℎ0 ⋯ ℎ 𝐿−1 01 0 𝑀−𝐿] 𝑇
Intervalo de guarda com CP permite tratar a operação de convolução
linear entre a resposta al impulso do canal e o sinal de tx CP-OFDM
como uma convolução circular](https://image.slidesharecdn.com/ofdm-final-160627223414/85/Ofdm-40-320.jpg)