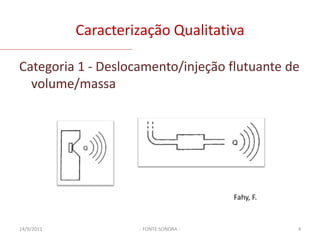
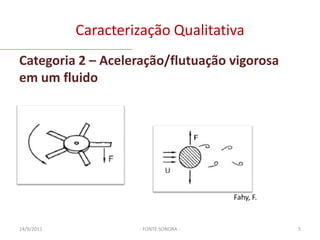
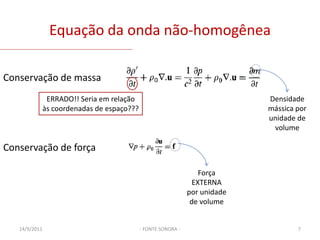
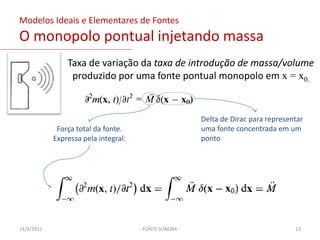
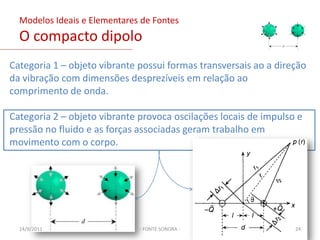
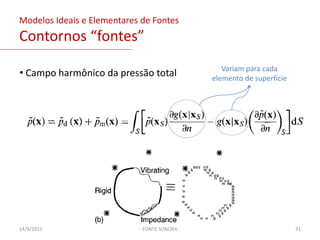
O documento discute modelos de fontes sonoras ideais, como monopolo e dipolo pontuais. Explica como uma esfera pulsante se aproxima de um monopolo e como uma esfera oscilante gera um campo de dipolo. Também aborda representar contornos como distribuições de fontes e resolver a equação da onda para diferentes configurações de fontes.

1. Fontes SonorasJoaquim PinheiroBrasília – DF, 03 de fevereiro de 2011

2. ProblematizaçãoVórtice de trança em tubo de sucção de hidrogeradores- FONTE SONORA -03/02/20112Barbosa, A.A.Soeiro, N.S.

3. Problematização“Para controlar um ruído é necessário entender como a onda é gerada” (Fahy, F.);Dimensionamento de uma fonte representativa da trança;Simulações computacionais;Teoria envolvida.- FONTE SONORA -03/02/20113

4. Caracterização QualitativaCategoria 1 - Deslocamento/injeção flutuante de volume/massa03/02/2011- FONTE SONORA -4Fahy, F.

5. Categoria 2 – Aceleração/flutuação vigorosa em um fluido - FONTE SONORA -Caracterização Qualitativa03/02/20115Fahy, F.

6. Caracterização QualitativaCategoria 3 – Flutuação de tensão de cisalhamento de fluidos- FONTE SONORA -03/02/20116Fahy, F.

7. Equação da onda não-homogênea- FONTE SONORA -Conservação de massaDensidade mássica por unidade de volumeERRADO!! Seria em relação às coordenadas de espaço???Conservação de forçaForça EXTERNA por unidade de volume03/02/20117

8. Equação da onda não-homogênea- FONTE SONORA -+03/02/20118

9. - FONTE SONORA -Equação da onda não-homogêneaEm casos onde o fluído é deslocado ao invés de injetado.

10. q– velocidade do volume por unidade de volume

11. Densidade da intensidade de um fonte monopoloEsta forma linearizada da equação não pode representar uma geração de som causada por um fluxo turbulento livre (ausência de superfície sólida). Porém, a flutuação de pressão causada por um regime turbulento numa superfície rígida pode ser representada por uma distribuição de forças externas f.03/02/20119

12. Equação da onda não homogêneaRadiação sonora por corpos externosDuas formas de resolver a equação1ª Condições de contorno – no lado direito apenas se representa as fontes ativas dentro do volume.2ª - São representadas o contorno mais as fontes internas ao volume como sendo termos de “fonte” no lado direito- FONTE SONORA -03/02/201110

13. Napresença de uma parede rígida:o campo sonoro é modificado mas não se gera energia sonora,a energia sonora pode ser dissipada se a parede possuir uma impedância resistiva finita;o movimento da propagação de ondas pode ser cancelado imaginando que a parede vibra com uma igual e oposta velocidade normal a irradiação;Uma parede rígida não gera energia sonora, mas umaalteração no campo sonoro pode ser atribuída pela presença de termos virtuais de fonte na equação daonda.- FONTE SONORA -Equação da onda não homogêneaContornos “fonte” refletem ou absorvem energia03/02/201111

14. Modelos Ideais e Elementares de FontesAs formas mais simples de um fonte sonora são regiões altamente concentradas de introdução instável de massa ou deslocamento de volume.O som gerado num espaço livre por uma fonte terá simetria esférica em volta da fonte – MONOPOLO;O DIPOLO representa a ação de forças externas que aparecem na equação da onda.- FONTE SONORA -03/02/201112

15. Modelos Ideais e Elementares de FontesO monopolo pontual injetando massa- FONTE SONORA -Taxa de variação da taxa de introdução de massa/volume produzido por uma fonte pontual monopolo em x = x0.Delta de Dirac para representar uma fonte concentrada em um pontoForça total da fonte.Expressa pela integral:03/02/201113

16. - FONTE SONORA -Modelos Ideais e Elementares de FontesO monopolo pontual injetando massaA equação da onda não-homegênea para a pressão de uma fonte pontual será:Função Delta de DiracDevido a característica da função Delta de Dirac, o lado direito será sempre igual à zero em qualquer ponto exceto na fonte em x0Recordando...03/02/201114

17. Modelos Ideais e Elementares de FontesO monopolo pontual injetando massa- FONTE SONORA - Para ser resolvida necessita de que as condições de contorno sejam especificadas;03/02/201115

18. Modelos Ideais e Elementares de FontesO monopolo pontual e a esfera pulsante- FONTE SONORA - Iniciamos com uma esfera de raio r=a, e então consideramos que no limite o raio tende a zero;

19. Deslocamento da superfície ;Amplitude complexa do deslocamento radial Assume-se a amplitude do deslocamento radial sendo muito menor que o raio para a linearidade acústica ser mantida;

20. A velocidade radial das partículas é igual a da superfície da esfera: Amplitude complexa da pressão:03/02/201116

21. Modelos Ideais e Elementares de FontesO monopolo pontual e a esfera pulsante- FONTE SONORA -?Combinando as 2 expressões, e adotando como sendo a Velocidade Volumétrica da Fonte, temos:Amplitude complexa da pressãoImpedância acústica específicaPotência sonora irradiada (média temporal)03/02/201117

22. Modelos Ideais e Elementares de FontesO monopolo pontual e a esfera pulsante- FONTE SONORA -Efeitos de ka(número de onda x raio da esfera)Se:Parte reativa predominante. O fluido reage por influencia da inércia da esfera.Parte resistiva predominante. O fluido reage por influencia da sua própria resistência.03/02/201118

23. Modelos Ideais e Elementares de FontesO monopolo pontual e a esfera pulsante- FONTE SONORA -Para ser um fonte pontual com raio desprezível, ka tende a zero, assim ficamos com:Amplitude complexa da pressãoImpedância acústica específicaPotência sonora irradiada (média temporal)03/02/201119

24. Modelos Ideais e Elementares de FontesO monopolo pontual e a esfera pulsante- FONTE SONORA -?Amplitude complexa da pressão--> Intensidade harmônica da fonte monopolo.--> Função harmônica de Green para espaços livres. * - representa a função de transferência que relaciona o espectro da intensidade sonora com o campo de pressão (para regime estacionário e fontes randômicas)03/02/201120

25. Modelos Ideais e Elementares de FontesO monopolo pontual e a esfera pulsante- FONTE SONORA -Função de Green para espaços livres para um monopolo harmônico pontualOnde: Sendo , g é uma solução da eq. abaixo para um harmônico no domínio do tempo de uma unidade de força sonora de um monopolo.

26. Princípio da reciprocidade acústica: 03/02/201121

27. Modelos Ideais e Elementares de FontesO monopolo pontual e a esfera pulsante- FONTE SONORA -Propagação sonora não-harmônica para um monopolo pontualSolução para um monopolo pontualAmplitude complexa da velocidade radial da partículaImpedância acústica específicaparaIntensidade sonora irradiada (média temporal)03/02/201122

28. Modelos Ideais e Elementares de FontesO monopolo pontual e a esfera pulsante- FONTE SONORA -Propagação sonora não-harmônica para um monopolo pontualCaracterística de uma fonte ineficiente:paraSe torna uma função assintótica, tão inclinada quanto maior for03/02/201123

29. Modelos Ideais e Elementares de FontesO compacto dipolo- FONTE SONORA -Categoria 1 – objeto vibrante possui formas transversais ao a direção da vibração com dimensões desprezíveis em relação ao comprimento de onda.Categoria 2 – objeto vibrante provoca oscilações locais de impulso e pressão no fluido e as forças associadas geram trabalho em movimento com o corpo.03/02/201124

30. - FONTE SONORA -Modelos Ideais e Elementares de FontesO compacto dipoloPropagação sonora para um compacto dipoloAmplitude complexa da pressãoOnde a Intensidade harmônica da fonte dipolo é:Amplitude complexa da velocidade radial da partículaImpedância acústica específicaparaIntensidade sonora irradiada (média temporal)03/02/201125

31. Modelos Ideais e Elementares de FontesO compacto dipoloPropagação sonora para um compacto dipoloSolução para um dipolo compactoDistribuição de pressãoPotência sonora total do dipolo- FONTE SONORA -03/02/201126

32. Modelos Ideais e Elementares de FontesO compacto dipoloComparação entre as potências sonoras da fonte monopolo e da dipoloSabendo disso, é possível distinguir uma fonte com características de monopolo para uma com características de dipolos em sistemas reais- FONTE SONORA -03/02/201127

33. Modelos Ideais e Elementares de FontesA esfera oscilanteUma esfera oscilante gera um campo sonoro próximo a ela de um dipolo pontual idealForça de reação do fluido sobre a esferaAmplitude complexa da pressãoPotência sonora total do dipolo- FONTE SONORA -03/02/201128