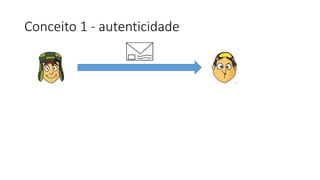
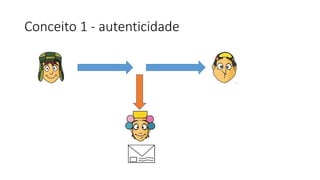
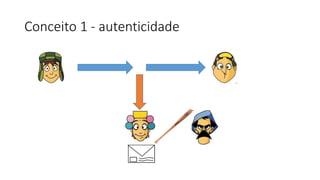
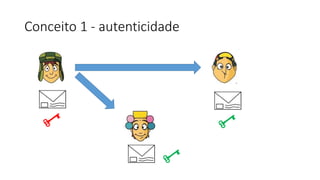
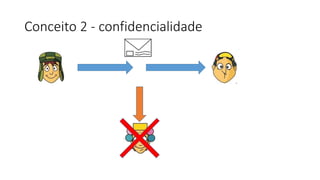
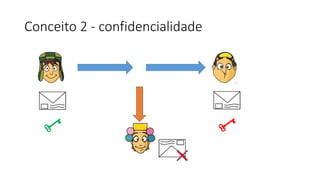
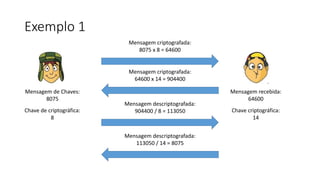
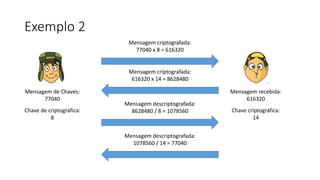
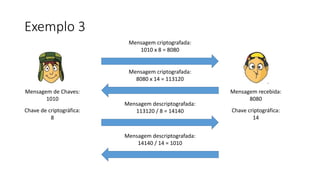
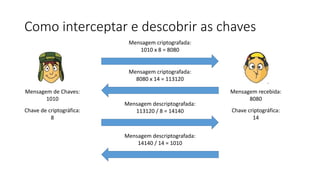
O documento discute criptografia de chave pública para permitir que Chaves envie mensagens secretas para Quico de forma autêntica e confidencial. A chave pública é distribuída para todos, enquanto a chave privada é secreta. Mensagens criptografadas com a chave privada só podem ser descriptografadas com a chave pública correspondente e vice-versa. Isso garante que apenas o destinatário apropriado possa ler a mensagem. Exemplos ilustram o processo.

1. Criptografia de chave pública
Rafael Amaral Salgueiroza

2. Situação-problema
• Chaves precisa enviar uma mensagem a Quico;
• Quico precisa ter certeza que foi Chaves que enviou;
• Chaves precisa ter certeza que apenas Quico pode abrir a mensagem;
• Ambos precisam ter certeza que a mensagem não será lida ou
alterada por terceiros.

3. Conceitos envolvidos
• Autenticidade
• Quico precisa ter certeza que foi Chaves que enviou
• Confidencialidade
• Chaves precisa ter certeza que apenas Quico pode abrir a mensagem

4. Chave pública e chave privada
• A chave pública não é secreta, é distribuída para todos.
• A chave privada é secreta, somente o dono sabe.
• O que é criptografado com a chave privada, somente pode ser lido
com a chave pública;
• O que é criptografado com a chave pública, somente pode ser lido
com a chave privada.

5. Conceito 1 - autenticidade

6. Conceito 1 - autenticidade

7. Conceito 1 - autenticidade

8. Conceito 1 - autenticidade

9. Conceito 2 - confidencialidade

10. Conceito 2 - confidencialidade

11. Exemplo 1
Mensagem de Chaves:
8075
Chave de criptográfica:
8
Mensagem criptografada:
8075 x 8 = 64600
Mensagem recebida:
64600
Chave criptográfica:
14
Mensagem criptografada:
64600 x 14 = 904400
Mensagem descriptografada:
904400 / 8 = 113050
Mensagem descriptografada:
113050 / 14 = 8075

12. Exemplo 2
Mensagem de Chaves:
77040
Chave de criptográfica:
8
Mensagem criptografada:
77040 x 8 = 616320
Mensagem recebida:
616320
Chave criptográfica:
14
Mensagem criptografada:
616320 x 14 = 8628480
Mensagem descriptografada:
8628480 / 8 = 1078560
Mensagem descriptografada:
1078560 / 14 = 77040

13. Exemplo 3
Mensagem de Chaves:
1010
Chave de criptográfica:
8
Mensagem criptografada:
1010 x 8 = 8080
Mensagem recebida:
8080
Chave criptográfica:
14
Mensagem criptografada:
8080 x 14 = 113120
Mensagem descriptografada:
113120 / 8 = 14140
Mensagem descriptografada:
14140 / 14 = 1010

14. Como interceptar e descobrir as chaves
Mensagem de Chaves:
1010
Chave de criptográfica:
8
Mensagem criptografada:
1010 x 8 = 8080
Mensagem recebida:
8080
Chave criptográfica:
14
Mensagem criptografada:
8080 x 14 = 113120
Mensagem descriptografada:
113120 / 8 = 14140
Mensagem descriptografada:
14140 / 14 = 1010

15. Conclusão
• A criptografia de chave pública resolve um problema antigo: a
comunicação de informações confidenciais.
• Garante a autenticidade quando assinado com a chave privada do
remetente;
• Garante a confidencialidade quando assinado com a chave pública do
destinatário

16. Obrigado.