Computação quântica 2012.2 presentation

Introdução à
Computação Quântica
(para computatas)
Wilson Rosa de Oliveira Jr.
20 e 27/11/2012
Seminários do
Quantum Computing Group DEInfo-UFRPE
http:www.ppgia.ufrpe.br/quantum
1Tuesday, November 20, 2012

Prolegomena
• Em Computação Quântica (CQ) testemunhamos a junção de
duas das áreas mais importantes na ciência do sec. XX:
– Mecânica Quântica e Informática
• Esta junção traz novos objetivos, desafios e
potencialidades para a Informática bem como novas
abordagens para a Física explorar o mundo quântico.
• Mesmo que seja no momento difícil prever impactos
particulares da CQ sobre a computação em geral,
esperamos que esta junção leve a resultados importantes

Mecânica Quântica é ...
• Uma teoria excelente para prever probabilidades de
eventos quânticos.
• Uma teoria elegante e conceitualmente simples que
descreve com precisão assustadora um amplo espectro de
fenômenos naturais:
– Experimentalmente verificadas a 14 ordens de precisão;
– Até o momento não há conflito entre o teoricamente previsto e o verificado
experimentalmente
• Sem MQ não podemos explicar propriedades dos
superfluidos, funcionamento dos lasers, a substância da
química, a estrutura e função do DNA, a existência e
comportamento de corpos sólidos, cor das estrelas,
semicondutores, etc

Mecânica Quântica trata ...
• Das entidades fundamentais da Física – partículas tais
como:
– Prótons, elétrons e nêutrons (que constituem a matéria);
– Fótons (que carregam radiação eletromagnética) – são as únicas partículas
que podemos observar diretamente;
– Várias outras “partículas elementares” que mediam outras interações da
Física.
• Partículas? Algumas de suas propriedades são totalmente
discordantes das propriedades do que chamamos de
partículas no nosso mundo usual!
• Propriedades? Não é claro em que sentido estas
“partículas” podem ser ditas possuir propriedades!

Mecânica Quântica
• Independente de sua qualidade, do ponto de
vista de explicar fenômenos quânticos, é uma
teoria muito insatisfatória!
• É uma teoria que tem princípios difíceis de
aceitar e leva a mistérios e paradoxos.

Algumas frases famosas
• Roger Penrose:
“Quantum theory seems to lead to philosophical standpoints
that many find deeply unsatisfying.
At best, and taking its descriptions at their most literal, it
provides us with a very strange view of the world indeed.
At worst, and taking literally the proclamations of some of
its most famous protagonists, it provides us with no view
of the world at all”

Algumas frases famosas
• Richard Feynman:
– “I think it is safe to say that no one understands
Quantum Mechanics”.
– “Nobody knows how it can be like that”.
• Bernard Shaw:
– “You have nothing to do but mention the quantum
theory, and people will take your voice for the voice of
science, and believe anything”.

Mas afinal o que MQ nos diz?
• Nos diz o que acontece
• Mas não diz porque acontece.
• E não nos diz como acontece.
• Nem quanto custa

Compreensão da FQ
Vou lhe dizer o que acontece na Natureza,
entretanto jamais pergunte a si mesmo:
“Mas como ela pode ser assim?”
Porque senão você será sugado para uma escuridão
da qual ninguém conseguiu até hoje escapar!
“Nobody knows how it can be like that”.
Feynman

Exemplo de estranheza:
Interferômetro de Mach-Zehnder

Uma outra visão da Mecânica
Quântica
• MQ não é Física no sentido usual – não é sobre
matéria ou energia ou onda ou partículas – é
sobre informação, probabilidades, amplitudes de
probabilidades e observáveis; e como eles se
relacionam entre si.
• MQ é o que se obtém quando se generaliza teoria
da probabilidade a permitir números negativos.
Poderia até ter sido descoberta pelos
matemáticos sem qualquer motivação dos
experimentos (Aaronson, 1997).

Por que Informação e Computação
Quântica é tão importante?
• ICP pode levar a novas tecnologias que terão impactos
amplos e profundos.
• Muitas das ciências e tecnologias já estão se aproximando
do ponto em que precisam isolar, manipular e transmitir
partículas.
• Novos conhecimentos sobre os fenômenos e sistemas
quânticos complexos podem ser gerados.
• Criptografia quântica nos leva a um novo patamar de
segurança.
• ICP tem se mostrado ser mais eficiente em situações
importante;interessantes.

Por que devemos tentar construir
computadores quânticos?
When you try to reach for stars you may not
quite get one, but you won’t come with a
handful of mud either.
Leo Burnett

Informação X Física
• Norbert Wiener:
– Informação é informação, nem matéria nem energia.
• Ralf Landauer:
– Informação é física.
• Deve então fazer parte da Física a Teoria da Informação e a Teoria da
Computação?
• Visão corrente:
– Física é informacional.
• Deve a mecânica quântica (espaços de Hilbert) fazer parte da
Informática?

Curiosidade
• Física Quântica é uma teoria extremamente
elaborada, cheia de paradoxos e mistérios. Leva-se
anos para um físico desenvolver um sentimento.
• Alguns teóricos da computação e matemáticos, sem
qualquer base em FQ têm realizado contri-buições
fundamentais a teoria da informação e computação
quântica!

Outra motivação
• Lei de Moore que prevê que em 2020
precisaremos de um elétron apenas para
amarzenar um bit!

Histórico (um pouco)
• Richard Feynman
– 1959: Nanotecnologia
•(“Há muito mais espaço lá embaixo”)‫‏‬
– 1982:
•Sistemas clássicos não modelam
eficientemente sistemas quânticos
•Sugere construção de computadores
baseados nas leis da mecânica quântica

Histórico
• David Deutsch
– 1985: MTQ (Máquina de Turing Quântica)‫‏‬
– 1989: publicou primeiro algoritmo quântico
•Problema de determinar se uma função
de um bit é cte ou balanceada.

Histórico
• Peter Shor
– 1993: Algoritmo de Shor
•Fatoração de números grandes
Tempo de Fatoração
pelo Algoritmo de Shor
Comprimento do número
a ser fatorado (bits)
Tempo de Fatoração
pelo Algoritmo de clássico
34s 512 4 dias
4.5m 1024 105 anos
36m 2048 1017 anos
4,8h 4096 1035 anos

Computação Clássica
• Mais precisamente: Modelos de Circuitos.
• Outros modelos não considerados aqui:
Máquinas de Turing, λ-Cálculo, Funções
Recursivas, etc.
• Mais próximo do computador digital

f : {0, 1}m
←→ {0, 1}n
f : {0, 1}m
←→ {0, 1}
ou

NAND é universal (crossover, fanout)

Computação Clássica - exemplos
Meio Somador (half adder)

Computação Clássica - exemplos
Somador Completo (full adder)

É uma seqüência enumerável de circuitos :
1. Os circuitos Cn têm n entradas e um números finito de bits
suplementares (ancilla) e de saída.
2. A saída de Cn é denotada por Cn(x) e é definida para todo
número binário x de no máximo n bits.
3. Se m<n e x tem no máximo m bits então Cm(x) = Cn(x).
É uma família uniforme de circuitos se existe um procedimento
efetivo que computa a descrição de Cn para todo n .
A família computa f:N→N se Cn(x(n))=f(x) todo número x e x(n) é a
representação binária de no máximo n bits de x .
Família consistentes de circuitos
{Cn}∞
n=0

Computação Clássica Reversível
• CNot

• Toffoli
Qualquer função f pode ser computada usando apenas Toffoli e crossover!

Quantização Matemática
• NiK Weaver (Washington University):
“Substituir conjuntos por um espaço de Hilbert
apropriado” e “funções por mapas lineares"
• O conjunto em consideração passa a ser visto
(representado) como uma base (ortonormal).
• As funções consideradas são as lineares (ou
subclasse destas).
• Finitamente dimensional = espaço vetorial

|α|2
+ |β|2
= 1
Classical Bits: Cbits
• bit abstrato: e
• Representação como cbit: e
–par de vetores ortonormais, e.g:
• Em R2
ou C2
•Um estado arbitrário:
|1|0
0 1
|0 =

1
0

|1 =

0
1

|ϕ = α |0 + β |1

F´ormula de Euler:
eiθ
= cos(θ) + i sin(θ)
Forma exponencial:
c = ρeiθ
|ψ = cos(θ) |0 + eiφ
sin(θ) |1

|0 ⊗ |0 , |0 ⊗ |1 , |1 ⊗ |0 , |1 ⊗ |1
|0 |0 , |0 |1 , |1 |0 , |1 |1
|00 , |01 , |10 , |11 ,
• quando precisarmos de mais de um Cbit:
produto tensorial

|02 |12 |22 |32
|xn 0 ≤ x 2n
|196 = |010011 = |0 |1 |0 |0 |1 |1
= |0 ⊗ |1 ⊗ |0 ⊗ |0 ⊗ |1 ⊗ |1
Notação

y0
y1

z0
z1

=




y0z0
y0z1
y1z0
y1z1





x0
x1

y0
y1

z0
z1

=












x0y0z0
x0y0z1
x0y1z0
x0y1z1
x1y0z0
x1y0z1
x1y1z0
x1y1z1













Operações

Portas Lógicas Quânticas Single-qbit
Hadamard gate
Phase gate
Pauli gates
=

Controlled-not gate
Control
Target U
Controlled-phase gate
Z
Exercício: Mostre que HZH = X.
Z
Z
=
Simetria faz
controlled-phase gate
mais natural para
implementação
X
=
ZH H
CNOT é
o caso quando
U=X

Toffoli gate
Control qubit 1
Target qubit
Control qubit 2
⊕

quantum NAND
Computando funções clássicas
quantum fanout
Circuito Classico Circuito Quântico
Text
|f(x)〉
|x〉
⊕⊕

• Medida de um estado |ϕ = α |0 + β |1
• {Mm}
p(m) = ϕ| M†
mMm |ϕ
– |0 com probabilidade |α|2
| e
– |1 com probabilidade |β|2
|
• Completeza
m
ϕ| M†
mMm |ϕ = I
• Me = |e e|
Medição: obtendo resultados
|β|2
|α|2
e

Conjugada Hermitiana; tomando a adjunta
Matrizes Unitárias
A é dita ser unitária se
Usualmente escrevemos unitárias como U.
Exemplo:

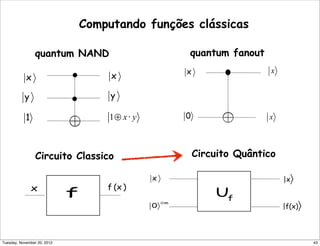
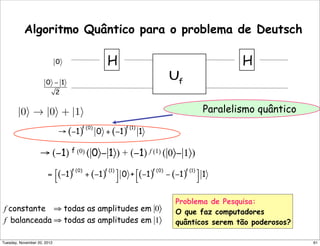
|ψ = |00+|11
√
2
Suponhamos que |ψ = |a |b. Ent˜ao:
|ψ = (α |0 + β |1)(γ |0 + δ |1)
= αγ |00 + βγ |10 + αδ |01 + βδ |11
Logo (β = 0 ou γ = 0) e (α = 0 ou δ = 0) o que ´e um absurdo!
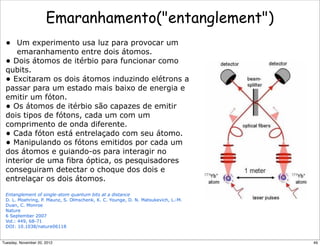
Emaranhamento (entanglement) Quântico
Alice Bob
Schroedinger (1935): “I would not call [entanglement] one but
rather the characteristic trait of quantum mechanics, the one that
enforces its entire departure from classical lines of thought.”

Estados Emaranhados
Considere os estados de 2-qubits:
|ψ〉 = 1/√2(|00 〉 + |11 〉) e |ϕ〉 = 1/√2(|00 〉 + |01 〉)
|ϕ〉 é composto do produto tensorial |0〉 ⊗ 1/√2(|0〉+|1〉)
Medição do segundo qubit resultará em |0〉ou |1 〉 com uma probabilidade ½ para
cada resultado, independente de o primeiro qubit ser medido ou não. Medição do
primeiro dará sempre |0 〉
|ψ〉 não pode ser decomposto em um produto de dois outros qubits
É um estado emaranhado!!.
A medição do primeiro determina completamente o resultado
do segundo.

|00
C
−→
1
√
2
(|00 + |11)
|01
C
−→
1
√
2
(|01 + |10)
|10
C
−→
1
√
2
(|00 − |11)
|01
C
−→
1
√
2
(|01 − |10)
|000
C
−→
1
√
2
(|000 + |111)
|001
C
−→
1
√
2
(|001 + |110)
· · ·etc
⊕
⊕
C-NOT em ação - Bell states
H H
⊕

Emaranhamento(entanglement)
• Um experimento usa luz para provocar um
emaranhamento entre dois átomos.
• Dois átomos de itérbio para funcionar como
qubits.
• Excitaram os dois átomos induzindo elétrons a
passar para um estado mais baixo de energia e
emitir um fóton.
• Os átomos de itérbio são capazes de emitir
dois tipos de fótons, cada um com um
comprimento de onda diferente.
• Cada fóton está entrelaçado com seu átomo.
• Manipulando os fótons emitidos por cada um
dos átomos e guiando-os para interagir no
interior de uma fibra óptica, os pesquisadores
conseguiram detectar o choque dos dois e
entrelaçar os dois átomos.
Entanglement of single-atom quantum bits at a distance
D. L. Moehring, P. Maunz, S. Olmschenk, K. C. Younge, D. N. Matsukevich, L.-M.
Duan, C. Monroe
Nature
6 September 2007
Vol.: 449, 68-71
DOI: 10.1038/nature06118

Cópia (Cloning)

Cópia (Cloning)
Estados quânticos não podem ser copiados ou clonados!

Cópia (Cloning)
Prova: Assuma uma transformação unitária U tal que U⏐a〉⏐0〉 =
⏐a〉⏐a〉.

Cópia (Cloning)
⏐a〉⏐a〉.
Sejam ⏐a〉 e ⏐b〉 estados ortogonais e

Cópia (Cloning)
⏐a〉⏐a〉.
U⏐a〉⏐0〉 = ⏐a〉⏐a〉 e U⏐b〉⏐0〉 = ⏐b〉⏐b〉

Cópia (Cloning)
⏐a〉⏐a〉.
U⏐a〉⏐0〉 = ⏐a〉⏐a〉 e U⏐b〉⏐0〉 = ⏐b〉⏐b〉
Considere agora ⏐c〉 = 1/√2(⏐a〉 + ⏐b〉)

Cópia (Cloning)
⏐a〉⏐a〉.
U⏐a〉⏐0〉 = ⏐a〉⏐a〉 e U⏐b〉⏐0〉 = ⏐b〉⏐b〉
Por linearidade,

Cópia (Cloning)
⏐a〉⏐a〉.
U⏐a〉⏐0〉 = ⏐a〉⏐a〉 e U⏐b〉⏐0〉 = ⏐b〉⏐b〉
Por linearidade,
U⏐c〉⏐0〉 = 1/√2(U⏐a〉⏐0〉 + U⏐b〉⏐0〉) = 1/√2(⏐a〉⏐a〉 + ⏐b〉⏐b〉)

Cópia (Cloning)
⏐a〉⏐a〉.
U⏐a〉⏐0〉 = ⏐a〉⏐a〉 e U⏐b〉⏐0〉 = ⏐b〉⏐b〉
Por linearidade,
U⏐c〉⏐0〉 = 1/√2(U⏐a〉⏐0〉 + U⏐b〉⏐0〉) = 1/√2(⏐a〉⏐a〉 + ⏐b〉⏐b〉)
Mas se U é uma transformação de cópia

Cópia (Cloning)
⏐a〉⏐a〉.
U⏐a〉⏐0〉 = ⏐a〉⏐a〉 e U⏐b〉⏐0〉 = ⏐b〉⏐b〉
Por linearidade,
U⏐c〉⏐0〉 = 1/√2(U⏐a〉⏐0〉 + U⏐b〉⏐0〉) = 1/√2(⏐a〉⏐a〉 + ⏐b〉⏐b〉)
U⏐c〉⏐0〉 = ⏐c〉⏐c〉 = 1/√2(⏐a〉 + ⏐b〉) ⊗ 1/√2(⏐a〉 + ⏐b〉)

Cópia (Cloning)
⏐a〉⏐a〉.
U⏐a〉⏐0〉 = ⏐a〉⏐a〉 e U⏐b〉⏐0〉 = ⏐b〉⏐b〉
Por linearidade,
U⏐c〉⏐0〉 = 1/√2(U⏐a〉⏐0〉 + U⏐b〉⏐0〉) = 1/√2(⏐a〉⏐a〉 + ⏐b〉⏐b〉)
U⏐c〉⏐0〉 = ⏐c〉⏐c〉 = 1/√2(⏐a〉 + ⏐b〉) ⊗ 1/√2(⏐a〉 + ⏐b〉)
= ½ (⏐a〉⏐a〉 + ⏐a〉⏐b〉 + ⏐a〉⏐b〉 + ⏐b〉⏐b〉)

Cópia (Cloning)
⏐a〉⏐a〉.
U⏐a〉⏐0〉 = ⏐a〉⏐a〉 e U⏐b〉⏐0〉 = ⏐b〉⏐b〉
Por linearidade,
U⏐c〉⏐0〉 = 1/√2(U⏐a〉⏐0〉 + U⏐b〉⏐0〉) = 1/√2(⏐a〉⏐a〉 + ⏐b〉⏐b〉)
U⏐c〉⏐0〉 = ⏐c〉⏐c〉 = 1/√2(⏐a〉 + ⏐b〉) ⊗ 1/√2(⏐a〉 + ⏐b〉)
= ½ (⏐a〉⏐a〉 + ⏐a〉⏐b〉 + ⏐a〉⏐b〉 + ⏐b〉⏐b〉)
Contradição!!
alalalalalalalalalal

Probabilidade?
P01=P10=0, P00=P11=1 computa identidade
P01=P10=1, P00=P11=0 computa um NOT
P01=P10=P00=P11=0.5 resulta 0 e 1 aleatoriamente
a=0 ou 1
ƒ:{0,1}→{0,1}
b=0 ou 1

Probabilidade?
Suponha que ao compor duas destas máquina obtemos
uma máquina inversora de 0s e 1s
Como pode? Não me pergunto como, mas posso mostrar que ...

Probabilidade?

Probabilidade Quântica

Curiosidade

Exemplo: Problema de Deutsch’s
Caixa preta Reversível
Caixa preta Quântica
Determinar se uma função f dada é constante ou balanceada.
Dada uma caixa preta computando f :{0,1} →{0,1}
Classicamente precisamos avaliar ambos f(0) e f(1)
Quanticamente precisamos apenas avaliar f uma única vez!

Esquematicamente ...
C1
C2
soma

Pondo informação na fase

|0 → |0 + |1
Algoritmo Quântico para o problema de Deutsch
H H
Paralelismo quântico
Problema de Pesquisa:
O que faz computadores
quânticos serem tão poderosos?
f constante ⇒ todas as amplitudes em |0〉
f balanceada ⇒ todas as amplitudes em |1〉
→ (−1) f (0) (|0〉−|1〉) + (−1) f (1) (|0〉−|1〉)

Beam us up Scotty!
…
How do I do that?
Here´s is the code

Circuito Teleportação
H
H x
y
circuito de criação
do Bell State
s
Inverso do circuito
de criação do Bell
State

Os detalhes ... (1)
Alice que enviar a Bob o estado:
Para tal, qdo estão juntos criam o estado
emaranhado:
Bob vai para o lugar dele ...
|ϕ = α |0 + β |1
|β00 =
|00 + |11
√
2

O estado geral do “sistema” é:
Aplicando um CNOT ao qubit de Alice:=
Os detalhes ... (2)
|ψ = |ϕ ⊗ |β00 = (α |0 + β |1) ⊗
|00 + |11
√
2
=
α(|000 + |011) + β(|100 + |111)
√
2
|ψ
= UX |ψ
=
α(UX |000 + UX |011) + β(UX |100 + UX |111)
√
2
=
α(|000 + |011) + β(|110 + |101)
√
2

Os detalhes ... (3)
Aplicando Hadamard ao primeiro qubit de Alice:
resulta em:
Nao esqueça que Bob está com o terceiro qubit!
|ψ
=
α |0 (|00 + |11)
√
2)
+
β |1 (|10 + |01)
√
2
|ψ
= H |ψ
=
αH |0 (|00 + |11)
√
2)
+
βH |1 (|10 + |01)
√
2
= α

|0 + |1
√
2

|00 + |11
√
2
+ β

|0 − |1
√
2

|10 + |01
√
2

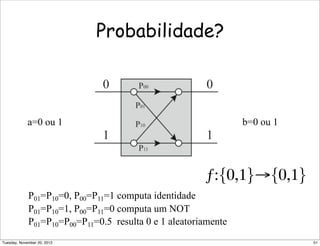
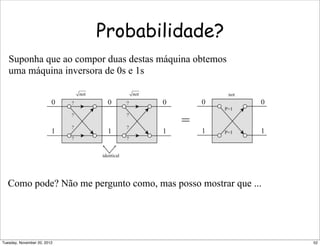
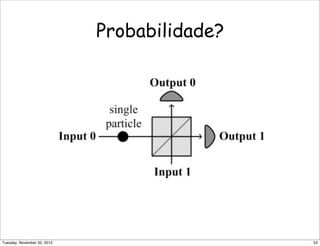
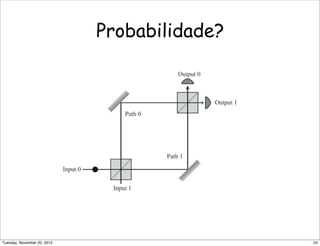
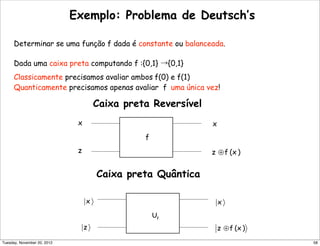
Os detalhes ... (4)
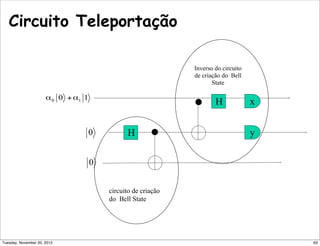
Alice mede seu par de qubits, onde o sistema
reescrito está em:
e Bob pode aplicar (resp.) I, X, Z e ZX ao resultado
para obetr o estado original.
Como saber o que aplicar?
|ψ
=
1
2
[|00 (α |0 + β |1) + |01 (α |1 + β |0) + |10 (α |0 − β |1) + |11 (α |1 − β |0)]

Os detalhes ... (5)
Alice telefone, etc por um cana clássico a Bob
informando o resultado de sua medição!

Busca Desestruturada de Grover
Dada uma lista desetruturada de tamanho N e uma
proposição P, encontre um x tal que P(x) seja
verdadeiro
Seja UP a porta quântica que implementa a função
booleana P(x) e n tal que 2n
≥ N.
UP : |x,0  |x,P(x)
UP operando na superposição de todos os estados da
base dá: 1/√2n
∑|x,P(x)
N-1
i=0
Se existe único estado tal que P(x)=1, a probailidade de
obter este estado após medição é apenas 1/√2n
Precisamos aumentar isto!!!
(verdadeiro)

Algoritmo de Shor
• Para fatorar N encontre x coprimo com N.
• Usa computador quântico encontrar r tal que xr
= 1 mod N.
• Se r é par, então mcd(xr/2
+1, xr/2
-1, N) é um fator de N que
podemos encontrar com o algoritmo de Euclides.

• Para fatorar N = 1295 seja x coprimo com N, e.g., x
= 6.
• Use um computador quântico para encontrar r tal
que 6r
= 1 mod 1295. r = 4.
• Se r é par, então mcd(64/2
-1, 64/2
+1, 1295) = mcd
(35, 37, 1295) é um fator de N que podemos
encontrar com o algoritmo Euclides. 1295 = 5 × 7 ×
37.
Algoritmo de Shor (exemplo)

Conclusões
• QC possui grande potencial
–Capacidade de um paralelismo exponencial
–Capacidade exponencial de armazenamento de
dados um espaço extremamente pequeno
• É possível utilizar:
–portas lógicas (quânticas)‫‏‬
–circuitos lógicos (quânticos)‫‏‬

Conclusões
• Não existe:
–PC
–Instruções
–Barramento
• Possui uma arquitetura completamente nova!!

Conclusões
• São necessários aperfeiçoamentos
–Nos instrumentos de indução das
transformações (RMN, laser)‫‏‬
–Necessidade de controle dos erros (melhorar as
formas de isolamento e interação com o sistema
quântico)‫‏‬

Conclusões
• Talvez a criação de um PC Quântico seja
muito complexa
• Solução: utilizar a computação quântica em
componentes de um PC

Meu interesse atual
• RAMs quânticas
• Programmable gates arrays
• Redes Neurais Quânticas (sem pesos)
• Quantum Computing + Chaos == resolvendo
problemas NP-completos em tempo polinomial.
• Modelos discretos da geometria differencial
(gravidade quântica) == Hypercomputação(?)
• Computação Relativística == Hypercomputação!

Referência
(por ordem de relevância)
1. Noson S. Yanofsky; Mirco A. Mannucci: Quantum Computing
for Computer Scientists. Cambridge University Press, 2008,
ISBN 978-0-521-87996-5
2. David McMahon: Quantum Computing Explained. Wiley-
Interscience, Hoboken, New Jersey, USA, 2008, ISBN
978-0-470-09699-4
3. N. David Mermin: Quantum Computer Science - An Introduc-
tion. Cambridge University Press, New York, USA, 2007, ISBN
978-0-521-87658-2
4. Alexei Yu. Kitaev, Alexander H. Shen e Mikhail N. Vyalyi:
Classical and Quantum Computation. Graduate Studies in

Computação quântica 2012.2 presentation

Recomendados

Recomendados

Mais conteúdo relacionado

Destaque

Destaque (12)

Último

Último (20)

Computação quântica 2012.2 presentation