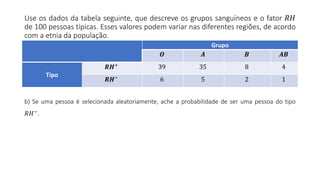
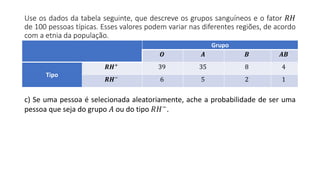
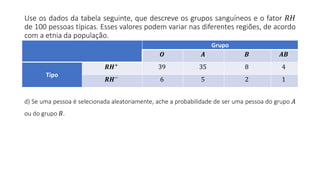
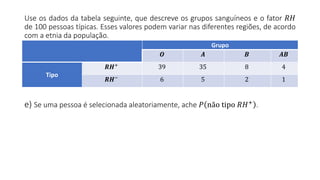
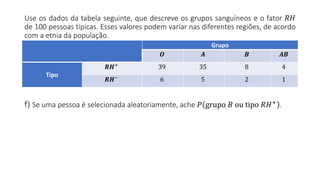
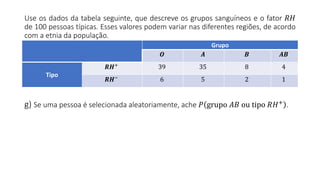
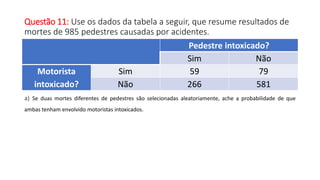
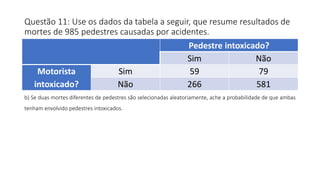
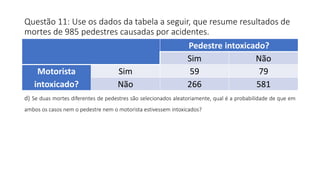
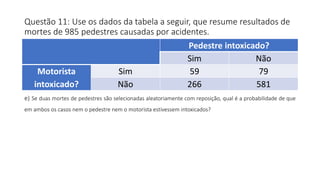
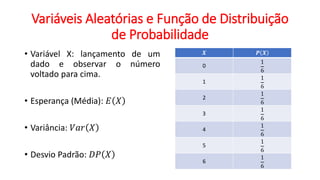
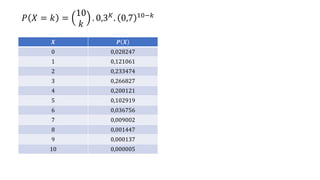
O documento apresenta dados estatísticos sobre grupos sanguíneos e fator RH de 100 pessoas para calcular probabilidades de vários eventos relacionados a esses dados. São feitos cálculos de probabilidade para 7 questões diferentes sobre selecionar pessoas aleatoriamente e verificar sua distribuição nos grupos sanguíneos e tipos RH.

1. Probabilidade

2. Use os dados da tabela seguinte, que descreve os grupos sanguíneos e o fator 𝑅𝐻
de 100 pessoas típicas. Esses valores podem variar nas diferentes regiões, de acordo
com a etnia da população.
Grupo
𝑶 𝑨 𝑩 𝑨𝑩
Tipo
𝑹𝑯+ 39 35 8 4
𝑹𝑯− 6 5 2 1
a) Se uma pessoa é selecionada aleatoriamente, ache a probabilidade de ser uma
pessoa que não pertence ao grupo 𝐴.

3. Use os dados da tabela seguinte, que descreve os grupos sanguíneos e o fator 𝑅𝐻
de 100 pessoas típicas. Esses valores podem variar nas diferentes regiões, de acordo
com a etnia da população.
Grupo
𝑶 𝑨 𝑩 𝑨𝑩
Tipo
𝑹𝑯+ 39 35 8 4
𝑹𝑯− 6 5 2 1
b) Se uma pessoa é selecionada aleatoriamente, ache a probabilidade de ser uma pessoa do tipo
𝑅𝐻−.

4. Use os dados da tabela seguinte, que descreve os grupos sanguíneos e o fator 𝑅𝐻
de 100 pessoas típicas. Esses valores podem variar nas diferentes regiões, de acordo
com a etnia da população.
Grupo
𝑶 𝑨 𝑩 𝑨𝑩
Tipo
𝑹𝑯+ 39 35 8 4
𝑹𝑯− 6 5 2 1
c) Se uma pessoa é selecionada aleatoriamente, ache a probabilidade de ser uma
pessoa que seja do grupo 𝐴 ou do tipo 𝑅𝐻−.

5. Use os dados da tabela seguinte, que descreve os grupos sanguíneos e o fator 𝑅𝐻
de 100 pessoas típicas. Esses valores podem variar nas diferentes regiões, de acordo
com a etnia da população.
Grupo
𝑶 𝑨 𝑩 𝑨𝑩
Tipo
𝑹𝑯+ 39 35 8 4
𝑹𝑯− 6 5 2 1
d) Se uma pessoa é selecionada aleatoriamente, ache a probabilidade de ser uma pessoa do grupo 𝐴
ou do grupo 𝐵.

6. Use os dados da tabela seguinte, que descreve os grupos sanguíneos e o fator 𝑅𝐻
de 100 pessoas típicas. Esses valores podem variar nas diferentes regiões, de acordo
com a etnia da população.
Grupo
𝑶 𝑨 𝑩 𝑨𝑩
Tipo
𝑹𝑯+ 39 35 8 4
𝑹𝑯− 6 5 2 1
e) Se uma pessoa é selecionada aleatoriamente, ache 𝑃 não tipo 𝑅𝐻+ .

7. Use os dados da tabela seguinte, que descreve os grupos sanguíneos e o fator 𝑅𝐻
de 100 pessoas típicas. Esses valores podem variar nas diferentes regiões, de acordo
com a etnia da população.
Grupo
𝑶 𝑨 𝑩 𝑨𝑩
Tipo
𝑹𝑯+ 39 35 8 4
𝑹𝑯− 6 5 2 1
f) Se uma pessoa é selecionada aleatoriamente, ache 𝑃 grupo 𝐵 ou tipo 𝑅𝐻+ .

8. Use os dados da tabela seguinte, que descreve os grupos sanguíneos e o fator 𝑅𝐻
de 100 pessoas típicas. Esses valores podem variar nas diferentes regiões, de acordo
com a etnia da população.
Grupo
𝑶 𝑨 𝑩 𝑨𝑩
Tipo
𝑹𝑯+ 39 35 8 4
𝑹𝑯− 6 5 2 1
g) Se uma pessoa é selecionada aleatoriamente, ache 𝑃 grupo 𝐴𝐵 ou tipo 𝑅𝐻+ .

9. Use os dados da tabela seguinte, que descreve os grupos sanguíneos e o fator 𝑅𝐻
de 100 pessoas típicas. Esses valores podem variar nas diferentes regiões, de acordo
com a etnia da população.
Grupo
𝑶 𝑨 𝑩 𝑨𝑩
Tipo
𝑹𝑯+ 39 35 8 4
𝑹𝑯− 6 5 2 1
h) Se uma pessoa é selecionada aleatoriamente, ache 𝑃 grupo 𝐴 ou 𝑂 ou tipo 𝑅𝐻+ .
P ( A U B U C ) = P ( A ) + P ( B ) + P ( C ) - P ( A ∩ B ) - P ( A ∩ C ) - P ( B ∩ C ) + P ( A ∩ B ∩ C )

10. Questão 11: Use os dados da tabela a seguir, que resume resultados de
mortes de 985 pedestres causadas por acidentes.
a) Se duas mortes diferentes de pedestres são selecionadas aleatoriamente, ache a probabilidade de que
ambas tenham envolvido motoristas intoxicados.
Pedestre intoxicado?
Sim Não
Motorista
intoxicado?
Sim 59 79
Não 266 581

11. Questão 11: Use os dados da tabela a seguir, que resume resultados de
mortes de 985 pedestres causadas por acidentes.
b) Se duas mortes diferentes de pedestres são selecionadas aleatoriamente, ache a probabilidade de que ambas
tenham envolvido pedestres intoxicados.
Pedestre intoxicado?
Sim Não
Motorista
intoxicado?
Sim 59 79
Não 266 581

12. Questão 11: Use os dados da tabela a seguir, que resume resultados de
mortes de 985 pedestres causadas por acidentes.
c) Se uma das mortes de pedestres é selecionada aleatoriamente, qual é a probabilidade de que envolva um
caso em que nem o pedestre nem o motorista estivessem intoxicados?
Pedestre intoxicado?
Sim Não
Motorista
intoxicado?
Sim 59 79
Não 266 581

13. Questão 11: Use os dados da tabela a seguir, que resume resultados de
mortes de 985 pedestres causadas por acidentes.
d) Se duas mortes diferentes de pedestres são selecionados aleatoriamente, qual é a probabilidade de que em
ambos os casos nem o pedestre nem o motorista estivessem intoxicados?
Pedestre intoxicado?
Sim Não
Motorista
intoxicado?
Sim 59 79
Não 266 581

14. Questão 11: Use os dados da tabela a seguir, que resume resultados de
mortes de 985 pedestres causadas por acidentes.
e) Se duas mortes de pedestres são selecionadas aleatoriamente com reposição, qual é a probabilidade de que
em ambos os casos nem o pedestre nem o motorista estivessem intoxicados?
Pedestre intoxicado?
Sim Não
Motorista
intoxicado?
Sim 59 79
Não 266 581

15. Questão 14:
Com um método de procedimento chamado amostragem de aceitação, uma
amostra de itens é selecionada aleatoriamente sem reposição, e o lote inteiro é
rejeitado se pelo menos um item na amostra for defeituoso. Uma companhia
acabou de fabricar 5000 aparelhos de pressão e 4% são defeituosos. Se 3 aparelhos
são selecionados e testados, qual é a probabilidade de que lote inteiro seja
recusado?

16. Exemplo:
Joana quer enviar uma carta a Camila. A probabilidade de que Joana escreve a carta
é
8
10
. A probabilidade de que o correio não a perca é
9
10
. A probabilidade de que o
carteiro a entregue é também
9
10
. Calcule a probabilidade de Camila não receber a
carta.

17. Exemplo:
Temos três profissionais: um Agronômo, um Biólogo e um Engenheiro Civil. Cada um
deles plantou 10 mudas de álamos. Das 10 plantadas pelo Agrônomo 9
sobreviveram; 5 do Biólogo e 2 do Engenheiro. Escolhe-se uma muda ao acaso, se a
muda sobreviveu, qual a probabilidade de ela ter sido plantada pelo Engenheiro
Civil?

18. Variáveis Aleatórias e Função de Distribuição
de Probabilidade
• Variável X: lançamento de um
dado e observar o número
voltado para cima.
• Esperança (Média): 𝐸 𝑋
• Variância: 𝑉𝑎𝑟 𝑋
• Desvio Padrão: 𝐷𝑃 𝑋
𝑿 𝑷 𝑿
0
1
6
1
1
6
2
1
6
3
1
6
4
1
6
5
1
6
6
1
6

19. Distribuição Binomial de Probabilidade
𝑃 𝑋 = 𝑘 =
𝑛
𝑘
. 𝑝𝐾. 1 − 𝑝 𝑛−𝑘
𝐸 𝑋 = 𝑛. 𝑝
𝑉𝑎𝑟 𝑋 = 𝑛. 𝑝. 𝑞
𝐷𝑃 𝑋 = 𝑉𝐴𝑅 𝑋

20. Distribuição Binomial de Probabilidade
Uma distribuição de probabilidade binomial resulta de um
experimento que satisfaz os seguintes requisitos:
1. O experimento tem um número fixo de tentativas.
2. As tentativas tem que ser independentes.
3. Cada tentativa deve ter todos os resultados classificados em duas
categorias (fracasso e sucesso).
4. A probabilidade de um sucesso permanece constante em todas as
tentativas.

21. Distribuição Binomial de Probabilidade
Num rebanho bovino 30% dos animais estão atacados de febre aftosa.
Retira-se ao acaso, uma amostra de 10 animais.
a) Verifique se a variável “número de animais doentes” pode ser estudada
pelo modelo binomial. Justifique.
1. O experimento tem um número fixo de tentativas. Temos 𝑛 = 10, então 𝑋 =
0, 1, 2, … , 10.
2. As tentativas tem que ser independentes. Os 10 animais são selecionados
aleatoriamente, isso garante a independência.
3. Cada tentativa deve ter todos os resultados classificados em duas categorias (fracasso
e sucesso). Um animal está ou não com febre aftosa.
4. A probabilidade de um sucesso permanece constante em todas as tentativas. A
probabilidade de cada animal de ter febre aftosa é constante.

22. Distribuição Binomial de Probabilidade
Num rebanho bovino 30% dos animais estão atacados de febre aftosa.
Retira-se ao acaso, uma amostra de 10 animais.
b) Estruturar a função de probabilidade e representar a distribuição de
probabilidade num gráfico.
𝑃 𝑋 = 𝑘 =
𝑛
𝑘
. 𝑝𝐾. 1 − 𝑝 𝑛−𝑘
𝑃 𝑋 = 𝑘 =
10
𝑘
. 0,3𝐾. 0,7 10−𝑘

23. 𝑃 𝑋 = 𝑘 =
10
𝑘
. 0,3𝐾
. 0,7 10−𝑘
𝑿 𝑷 𝑿
0 0,028247
1 0,121061
2 0,233474
3 0,266827
4 0,200121
5 0,102919
6 0,036756
7 0,009002
8 0,001447
9 0,000137
10 0,000005

25. Distribuição Binomial de Probabilidade
Num rebanho bovino 30% dos animais estão atacados de febre aftosa.
Retira-se ao acaso, uma amostra de 10 animais.
c) Qual a probabilidade de se encontrar 6 animais doentes.

26. Distribuição Binomial de Probabilidade
Num rebanho bovino 30% dos animais estão atacados de febre aftosa.
Retira-se ao acaso, uma amostra de 10 animais.
d) Qual a probabilidade de se encontrar no mínimo 2 animais doentes?

27. Distribuição Binomial de Probabilidade
Num rebanho bovino 30% dos animais estão atacados de febre aftosa.
Retira-se ao acaso, uma amostra de 10 animais.
e) Determine a 𝐸 𝑋 , 𝑉𝑎𝑟 𝑋 e 𝐷𝑃 𝑋 .

28. Distribuição de Poisson
𝑃 𝑋 = 𝐾 =
𝝁𝒙 ∙ 𝒆−𝝁
𝒙!
A média é 𝜇.
Desvio padrão é 𝜎 = 𝜇
Contagem de indivíduos, plantas, colônias de bactérias, etc, num
intervalo de tempo, área, volume ou comprimento. (contagens baixas).

29. Distribuição de Poisson
Exemplo: Numa área dividida em quadrantes de 0,50 m², foram
encontradas em média 2,5 espécimes. Considerando que o modelo de
Poisson é adequado, qual é a probabilidade de se encontrar num
quadrante exatamente 4 espécimes? Seja 𝑋 o número de espécimes
por 0,5 𝑚2
.

30. Distribuição de Poisson
Exemplo: Numa área dividida em quadrantes de 0,50 m², foram
encontradas em média 2,5 espécimes. Considerando que o modelo de
Poisson é adequado, qual é a probabilidade de se encontrar no máximo
1 espécime por quadrante?

31. Distribuição de Poisson
Exemplo: Numa placa microscópica, dividida em quadrantes de 1 mm²,
encontra-se em média 5 colônias por mm². Considerando que a
distribuição de Poisson é adequada, determine a probabilidade de um
quadrante ter exatamente 1 colônia.

32. Distribuição de Poisson
Exemplo: Numa placa microscópica, dividida em quadrantes de 1 mm²,
encontra-se em média 5 colônias por mm². Considerando que a
distribuição de Poisson é adequada, determine a probabilidade de se
encontrar 8 colônias em 2 mm².

33. Distribuição Normal
𝑍 =
𝑥 − 𝜇
𝜎

34. Distribuição Normal
• Determinar a área limitada pela curva normal:
Entre 𝑧 = 0 e 𝑧 = 1,2

35. Distribuição Normal
• Determinar a área limitada pela curva normal:
Entre 𝑧 = −0,68 e 𝑧 = 0

36. Distribuição Normal
• Determinar a área limitada pela curva normal:
Entre 𝑧 = 0,46 e 𝑧 = 2,21

37. Distribuição Normal
• Determinar a área limitada pela curva normal:
À esquerda de 𝑧 = −0,6

38. Distribuição Normal
• Determinar a área limitada pela curva normal:
À direita de 𝑧 = −1,23

39. Distribuição Normal
• Determinar a área limitada pela curva normal:
Entre 𝑧 = −1,98 e 𝑧 = +1,96

40. Distribuição Normal
Exemplo: A altura dos indivíduos de uma população distribui-se
normalmente com média de 1,56 m e desvio padrão de 0,09 m. Qual a
porcentagem nesta população de indivíduos com altura de 1,80 m ou
mais?