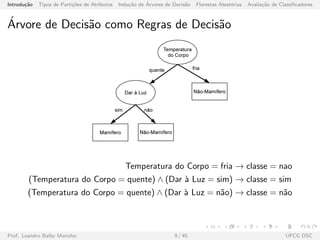
O documento discute a indução de árvores de decisão e classificação. Apresenta os componentes da aprendizagem de máquina para classificação e como árvores de decisão podem ser usadas para classificar instâncias em classes. Descreve também a formalização do problema de indução de árvores de decisão e o processo de busca gulosa usado para construir as árvores.




![Introdu¸c˜ao Tipos de Parti¸c˜oes de Atributos Indu¸c˜ao de ´Arvores de Decis˜ao Florestas Aleat´orias Avalia¸c˜ao de Classificadores
Componentes da Aprendizagem [Yaser, 2012]
Prof. Leandro Balby Marinho 5 / 45 UFCG DSC](https://image.slidesharecdn.com/arvoredecisaoadi-150614194558-lva1-app6891/85/Arvores-de-Decisao-6-320.jpg)
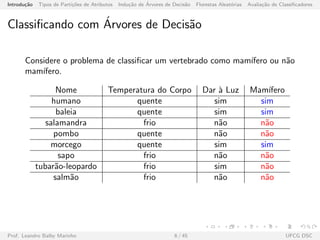
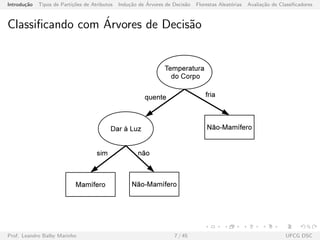






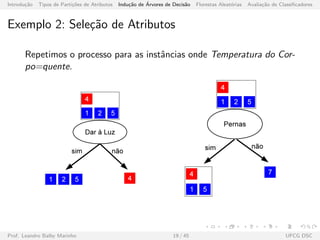

![Introdu¸c˜ao Tipos de Parti¸c˜oes de Atributos Indu¸c˜ao de ´Arvores de Decis˜ao Florestas Aleat´orias Avalia¸c˜ao de Classificadores
Fronteira de Decis˜ao [Tan, 2007]
0.0 0.2 0.4 0.6 0.8 1.0
0.00.20.40.60.81.0
0.1
0.1
q
q
q
q
q
q
q
As fronteiras de decis˜ao s˜ao retil´ıneas.
Prof. Leandro Balby Marinho 22 / 45 UFCG DSC](https://image.slidesharecdn.com/arvoredecisaoadi-150614194558-lva1-app6891/85/Arvores-de-Decisao-26-320.jpg)
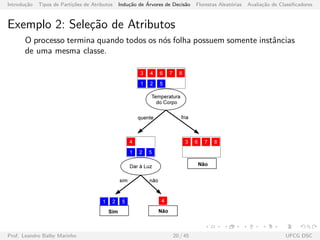
![Introdu¸c˜ao Tipos de Parti¸c˜oes de Atributos Indu¸c˜ao de ´Arvores de Decis˜ao Florestas Aleat´orias Avalia¸c˜ao de Classificadores
Medidas de Impureza de Atributos
As medidas mais usadas para a sele¸c˜ao de atributos s˜ao entropia,
coeficiente de Gini e erro de classifica¸c˜ao.
Seja p(y|t) a probabilidade condicional da classe y ∈ Y no n´o t. As
medidas s˜ao dadas abaixo:
Entropia(t) := −
y∈Y
p(y|t) log2 p(y|t)
Gini(t) := 1 −
y∈Y
p(y|t)2
Erro Class(t) := 1 − max
y∈Y
[p(y|t)]
Prof. Leandro Balby Marinho 23 / 45 UFCG DSC](https://image.slidesharecdn.com/arvoredecisaoadi-150614194558-lva1-app6891/85/Arvores-de-Decisao-27-320.jpg)
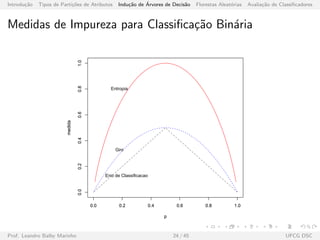
![Introdu¸c˜ao Tipos de Parti¸c˜oes de Atributos Indu¸c˜ao de ´Arvores de Decis˜ao Florestas Aleat´orias Avalia¸c˜ao de Classificadores
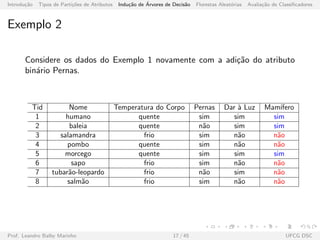
Exemplo 3
N´o N1 # Instˆancias
Classe=0 0
Classe=1 6
Gini = 1 − (0/6)2
− (6/6)2
= 0
Entropia = − (0/6) log2(0/6) − (6/6) log2(6/6) = 0
Erro Class = 1 − max[0/6, 6/6] = 0
Prof. Leandro Balby Marinho 25 / 45 UFCG DSC](https://image.slidesharecdn.com/arvoredecisaoadi-150614194558-lva1-app6891/85/Arvores-de-Decisao-29-320.jpg)
![Introdu¸c˜ao Tipos de Parti¸c˜oes de Atributos Indu¸c˜ao de ´Arvores de Decis˜ao Florestas Aleat´orias Avalia¸c˜ao de Classificadores
Exemplo 3
N´o N2 # Instˆancias
Classe=0 1
Classe=1 5
Gini = 1 − (1/6)2
− (5/6)2
= 0.278
Entropia = − (1/6) log2(1/6) − (5/6) log2(5/6) = 0.650
Erro Class = 1 − max[1/6, 5/6] = 0.167
Prof. Leandro Balby Marinho 25 / 45 UFCG DSC](https://image.slidesharecdn.com/arvoredecisaoadi-150614194558-lva1-app6891/85/Arvores-de-Decisao-30-320.jpg)
![Introdu¸c˜ao Tipos de Parti¸c˜oes de Atributos Indu¸c˜ao de ´Arvores de Decis˜ao Florestas Aleat´orias Avalia¸c˜ao de Classificadores
Exemplo 3
N´o N3 # Instˆancias
Classe=0 3
Classe=1 3
Gini = 1 − (3/6)2
− (3/6)2
= 0.5
Entropia = − (3/6) log2(3/6) − (3/6) log2(3/6) = 1
Erro Class = 1 − max[3/6, 3/6] = 0.5
Prof. Leandro Balby Marinho 25 / 45 UFCG DSC](https://image.slidesharecdn.com/arvoredecisaoadi-150614194558-lva1-app6891/85/Arvores-de-Decisao-31-320.jpg)

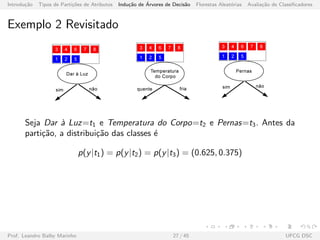
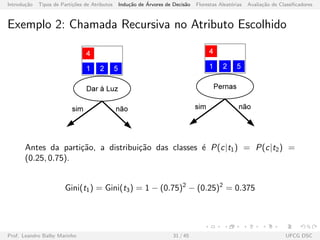
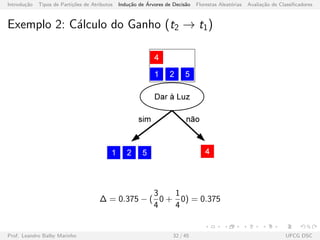
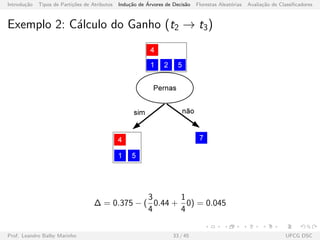


![Introdu¸c˜ao Tipos de Parti¸c˜oes de Atributos Indu¸c˜ao de ´Arvores de Decis˜ao Florestas Aleat´orias Avalia¸c˜ao de Classificadores
Algoritmo DecisionTree [Lars, 2011]
DecisionTree(NodeT, Dtrain)
1 if stop criterion(Dtrain)
2 T.class = argmaxy∈Y p(y|t)
3 return
4 s = find best split(Dtrain)
5 T.split = s
6 for z ∈ Im(s)
7 cria no T
8 T.child[z] = T
9 DecisionTree(T , {(x, y) ∈ Dtrain | s(x) = z})
Prof. Leandro Balby Marinho 36 / 45 UFCG DSC](https://image.slidesharecdn.com/arvoredecisaoadi-150614194558-lva1-app6891/85/Arvores-de-Decisao-43-320.jpg)


![Introdu¸c˜ao Tipos de Parti¸c˜oes de Atributos Indu¸c˜ao de ´Arvores de Decis˜ao Florestas Aleat´orias Avalia¸c˜ao de Classificadores
Tree Bagging [Wikipedia, 2013]
Existem muitos algoritmos de florestas aleat´orias. Abaixo
descrevemos um dos mais simples.
Para b = 1, . . . , B (B =nr. de ´arvores):
1. Amostre n instˆancias aleat´orias de treino sem repeti¸c˜ao e
chame-as de Tb ∈ Dtrain
.
2. Treine uma ´arvore de decis˜ao gb para cada Tb.
Agora a predi¸c˜ao para algum x cuja classe ´e desconhecida ´e
feita por:
ˆg(x ) = argmax
y∈Y
B
b=1
δ ˆgb(x , y)
Ou seja, use o voto majorit´ario entre as ´arvores da floresta.
Prof. Leandro Balby Marinho 39 / 45 UFCG DSC](https://image.slidesharecdn.com/arvoredecisaoadi-150614194558-lva1-app6891/85/Arvores-de-Decisao-47-320.jpg)