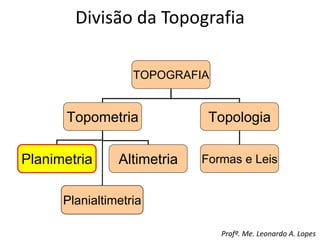
1) O documento descreve os principais conceitos da topografia, incluindo definições, divisões, ângulos, equipamentos e métodos de medição.
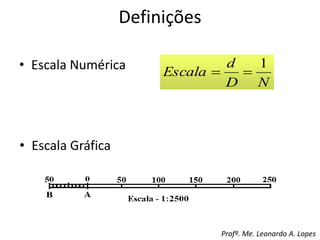
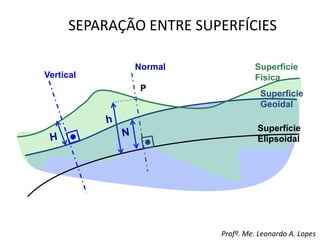
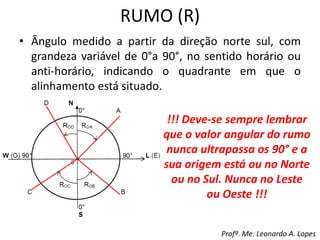
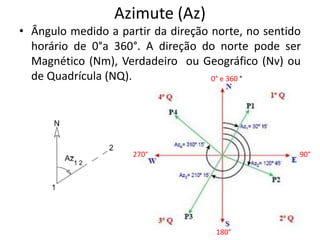
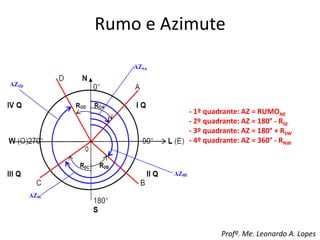
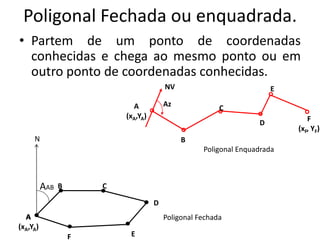
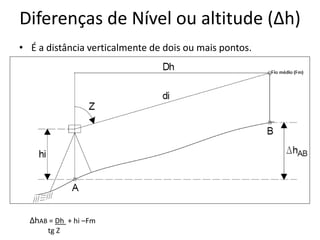
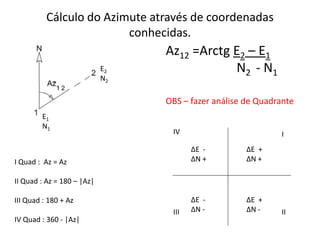
2) São apresentadas definições de termos como planimetria, altimetria, poligonal, azimute e diferença de nível.
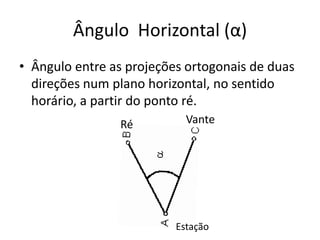
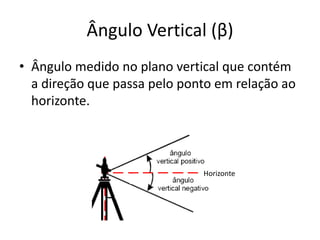
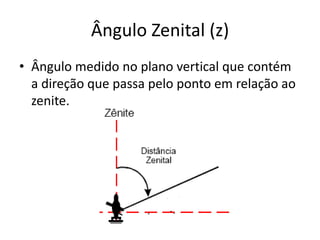
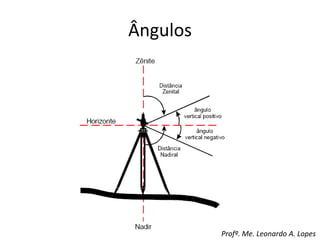
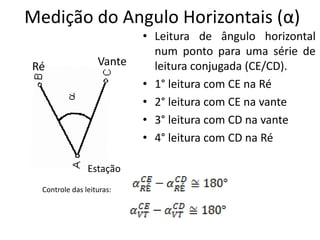
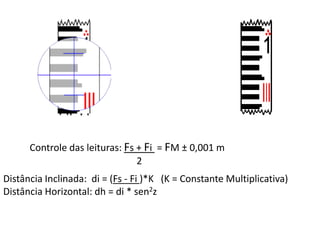
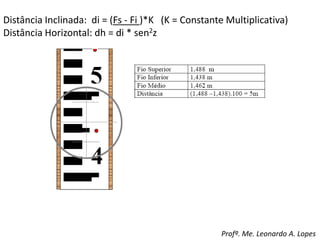
3) Detalha os tipos de ângulos utilizados em topografia como horizontais, verticais e zenitais e como são medidas as distâncias e altitudes.