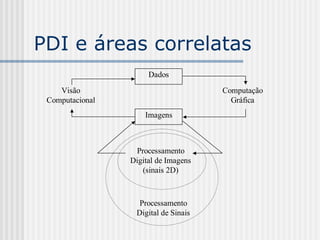
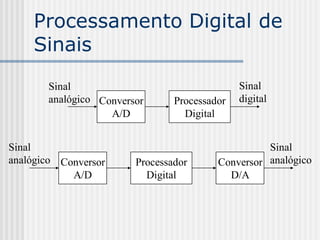
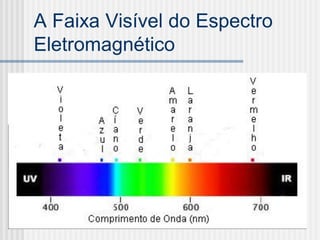
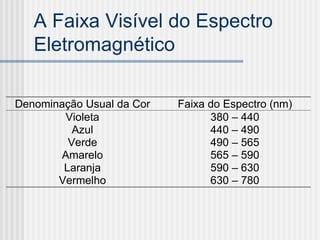
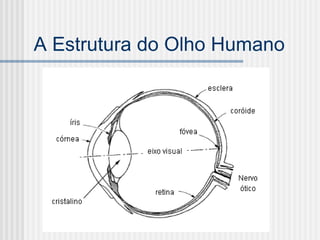
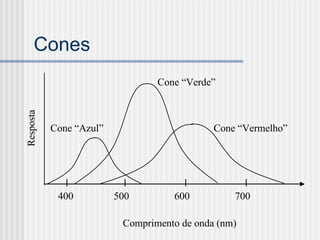
Este documento introduz o Processamento Digital de Imagens, definindo-o como a modelagem, análise, projeto e implementação de sistemas voltados ao tratamento de informação pictórica com fins estéticos ou de eficiência. Em seguida, apresenta as áreas correlatas ao PDI e exemplos de aplicações de imagens digitais antes de explicar conceitos-chave como amostragem, quantização, sistemas de cores e estrutura do olho humano.

1. Introdução ao
Processamento Digital de
Imagens
Prof. Leonardo Vidal Batista
DI/PPGI/PPGEM
leonardo@di.ufpb.br
leovidal@terra.com.br
http://www.di.ufpb.br/leonardo

2. Processamento Digital de
Imagens
 Modelagem matemática, análise, projeto
e implementação (S&H) de sistemas
voltados ao tratamento de informação
pictórica, com fins estéticos, para torná-la
mais adequada à interpretação ou
aumentar eficiência de armazenamento e
transmissão.

3. PDI e áreas correlatas
Dados
Visão Computação
Computacional Gráfica
Imagens
Processamento
Digital de Imagens
(sinais 2D)
Processamento
Digital de Sinais

4. PDI x Visão Computacional

5. Imagens digitais
 TV digital
 Câmeras digitais, celulares, scanners
 DVDs
 Sistemas de teleconferência
 Transmissões via fax
 Editoração eletrônica
 Impressoras
 Monitoramento da superfície terrestre e previsão
climática por imagens de satélites
 Detecção de movimento

6. Imagens Digitais
 Diagnóstico médico: ultrassonografia,
angiografia, tomografia, ressonância
magnética, contagem de células, etc
 Identificação biométrica: reconhecimento de
face, íris ou impressões digitais
 Ciências forenses
 Realce e restauração de imagens por
computador
 Instrumentação
 Controle de qualidade
 Granulometria de minérios

7. Outros Sinais Digitais
 Diagnóstico médico: eletrocardiograma,
eletroencefalograma, eletromiograma,
eletroretinograma, polisonograma, etc
 Identificação biométrica por reconhecimento
de voz
 Síntese de voz
 Áudio Digital
 Telefonia
 Suspensão ativa em automóveis
 Mercado acionário

8. Sinais Contínuos e Discretos
Sinal analógico
Sinal digital
...
Amplitude
2q
q
0
-q
-2q
...
Erros
de
quantização 0 Ta 2Ta 3Ta ...
Tempo, espaço etc.

9. Processamento Analógico
de Sinais
Processador
Sinal analógico analógico Sinal analógico
de entrada de saída

10. Processamento Digital de
Sinais
Sinal Sinal
analógico Conversor Processador digital
A/D Digital
Sinal Sinal
analógico Conversor Processador Conversor analógico
A/D Digital D/A

11. Processamento Digital de
Sinais
 Alguns sinais são inerentemente digitais ou
puramente matemáticos
 Ex: Número de gols por rodada do
campeonato brasileiro de futebol
 Neste caso, não há necessidade de
Conversão A/D
 Ainda assim, pode haver necessidade de
conversão D/A
 Ex: texto -> voz sintetizada

12. Processamento Digital de
Sinais
 Hardware, software, ou ambos
 Maior flexibilidade
 Menor custo
 Menor tempo de desenvolvimento
 Maior facilidade de distribuição
 Sinais digitais podem ser armazenados e
reproduzidos sem perda de qualidade
 Mas alguns sistemas exigem uma etapa
analógica!

13. Processamento Digital de
Sinais – Robustez a Ruído
Sinal analógico original
Sinal analógico corrompido – em geral, recuperação
impossível mesmo para pequenas distorções

14. Processamento Digital de
Sinais – Robustez a Ruído
Sinal digital corrompido – recuperação possível
Sinal digital original mesmo com distorções substanciais, principalmente
com uso de códigos corretores.
„1‟ „1‟
„0‟ „0‟
Sinal digital
recuperado com erro
„1‟
„0‟

15. Eliminação de ruído

16. Detecção de Bordas

17. Aguçamento

18. Pseudo-cor

19. Pseudo-cor

20. Segmentação/Classificação

21. Combinação de Imagens

22. Metamorfose

23. Warping (Deformação)

24. Warping (Deformação)
 Interpol faz apelo público para identificar
pedófilo
(http://noticias.terra.com.br/mundo/interna
/0,,OI1971484-EI294,00.html)
 As fotos haviam sido manipuladas
digitalmente para disfarçar o rosto do
pedófilo, mas especialistas em computação
da Agência de Polícia Federal na Alemanha
conseguiram reproduzir o rosto do suspeito
de forma que seja identificável

25. Warping (Deformação)
 A imagem distorcida pôde ser recuperada por
especialistas para que o homem fosse identificado

26. Você confia em seu sistema
visual?

27. Você confia em seu sistema
visual?

28. Você confia em seu sistema
visual?

29. Você confia em seu sistema
visual?
http://www.echalk.co.uk/
amusements/OpticalIllusi
ons/illusions.htm

30. Você confia em seu sistema
visual?

31. Você confia em seu sistema
visual?

32. Você confia em seu sistema
visual?

33. Você confia em seu sistema
visual?

34. Você confia em seu sistema
visual?

35. Você confia em seu sistema
visual?

36. Você confia em seu sistema
visual?

37. Você confia em seu sistema
visual?

38. Você confia em seu sistema
visual?

39. A Faixa Visível do Espectro
Eletromagnético
 Luz: radiação eletromagnética
 Freqüência f, comprimento de onda
L
 Faixa visível do espectro
eletromagnético: 380 nm < L < 780
nm
 Na faixa visível, o sistema visual
humano (SVH) percebe
comprimentos de onda diferentes
como cores diferentes

40. A Faixa Visível do Espectro
Eletromagnético
 Radiação monocromática: radiação
em um único comprimento de onda
 Cor espectral pura: radiação
monocromática na faixa visível

41. A Faixa Visível do Espectro
Eletromagnético

42. A Faixa Visível do Espectro
Eletromagnético
Denominação Usual da Cor Faixa do Espectro (nm)
Violeta 380 – 440
Azul 440 – 490
Verde 490 – 565
Amarelo 565 – 590
Laranja 590 – 630
Vermelho 630 – 780

43. A Estrutura do Olho Humano
 Olho humano: aproximadamente esférico,
diâmetro médio em torno de dois
centímetros
 A luz penetra no olho passando pela
pupila e pelo cristalino e atingindo a
retina
 Imagem invertida do cenário externo
sobre a retina
 Cones e bastonetes convertem energia
luminosa em impulsos elétricos que são
transmitidos ao cérebro.

44. A Estrutura do Olho Humano

45. Bastonetes
 75 a 150 milhões/olho, sobre toda a
retina
 Não são sensíveis às cores
 Baixa resolução (conectados em grupos
aos terminais nervosos)
 Sensíveis à radiação de baixa intensidade
na faixa visível
 Visão geral e de baixa luminosidade
 Objetos acinzentados sob baixa
luminosidade

46. Cones
 6 a 7 milhões/olho, concentrados na fóvea
 Sensíveis às cores
 Alta resolução (um cone por terminal
nervoso)
 Pouco sensíveis a radiação de baixa
intensidade na faixa visível
 Visão específica, de alta luminosidade
 Movimentamos os olhos para que a
imagem do objeto de interesse recaia
sobre a fóvea.

47. Cones
 Há três tipos de cones:
 Cone sensível ao vermelho
 Cone sensível ao verde
 Cone sensível ao azul
 Cores diversas obtidas por combinações
destas cores primárias

48. Cones
Cone “Verde”
Resposta
Cone “Azul” Cone “Vermelho”
400 500 600 700
Comprimento de onda (nm)

49. Sistema de Cores RGB
 A cor de uma fonte de radiação na
faixa visível é definida pela adição
das cores espectrais emitidas –
sistema aditivo
 Combinação de radiações
monocromáticas vermelho (R), verde
(G) e azul (B)
 Cores primárias da luz
 Sistema de cores RGB

50. Sistema RGB
 Padronização da Comissão
Internacional de Iluminação (CIE):
 Azul: 435,8 nm
 Verde: 546,1 nm
 Vermelho: 700 nm

51. Sistema RGB - Combinação de
Cores Primárias
 Cores secundárias da luz: magenta
(M), cíano (C) e amarelo (Y):
M = R + B
C = B + G
Y = G + R
 Cor branca (W):
W = R + G + B

52. Espaço de Cores RGB
 Cor no sistema RGB é um vetor em
um espaço tridimensional:
G
R
B

53. Espaço de Cores RGB
 Reta (i, i, i): reta acromática
 Pontos na reta acromática:
tonalidades de cinza ou níveis de
cinza
 Preto: (0, 0, 0) (ausência de luz)
 Branco: (M, M, M), (M é a intensidade
máxima de uma componente de cor)
 Monitor de vídeo: Sistema RGB

54. Sistema de Cores CMY
 Cor de um objeto que não emite
radiação própria depende dos
pigmentos que absorvem radiação
em determinadas faixas de
freqüência e refletem outras
 Absorção em proporções variáveis
das componentes R, G e B da
radiação incidente: sistema
subtrativo

55. CMY - Cores Primárias
 Cores primárias dos pigmentos:
absorvem uma cor primária da luz e
refletem as outras duas
C = W – R = G + B
M = W – G = R + B
Y = W – B = G + R

56. CMY – Combinação de Cores
Primárias
 Cores secundárias:
R = M + Y
G = C + Y
B = M + C
 Preto (K):
K = C + M + Y = W – R – G – B
 Impressoras coloridas: CMY ou CMYK

57. Processos Aditivo e Subtrativo

58. Sistema de Cores YIQ
 Transmissão de TV em cores:
compatibilidade com TV P & B
 Y: luminância (intensidade percebida,
ou brilho)
 I e Q: crominâncias

59. Conversão YIQ-RGB
 Conversão de RGB para YIQ:
 Y = 0.299R + 0.587G + 0.114B
 I = 0.596R – 0.274G –0.322B
 Q = 0.211R – 0.523G + 0.312B
 Conversão de YIQ para RGB :
 R = 1.000 Y + 0.956 I + 0.621 Q
 G = 1.000 Y – 0.272 I – 0.647 Q
 B = 1.000 Y – 1.106 I + 1.703 Q

60. Sistema de Cores HSI
 Fisiologicamente, a retina humana
opera no sistema RGB
 A percepção subjetiva de cor é
diferente
 Atributos perceptivos das cores:
 Matiz (hue) ou tonalidade
 Saturação
 Intensidade

61. Sistema de Cores HSI
 Matiz (H): determinada pelo comprimento
de onda dominante; cor espectral mais
próxima; denominação usual das cores
 H é um ângulo: 0o = R; 120o = G; 240o =
B
 Saturação: pureza da cor quanto à adição
de branco
 S = 0: cor insaturada (nível de cinza)
 S = 1: cor completamente saturada
 Cores espectrais puras tem S = 1

62. Sistema de Cores HSI
 Também chamado HSB, HSV, HSL
(B=Brightness; V=Value; L=Lightness), às vezes
com pequenas diferenças na conversão para
RGB.

63. Conversão HSI-RGB
 Algoritmos nas Notas de Aula

64. Imagem monocromática
y
x

65. Imagem monocromática
 Função Ia(x,y)
 (x, y): coordenadas espaciais
 Ia(x,y): intensidade ou brilho da
imagem em (x,y)

66. Amostragem e Quantização
 Digitalização: discretização espacial
(amostragem) e de intensidade
(quantização)

67. Amostragem e Quantização
Sinal analógico
Sinal digital
...
Amplitude
2q
q
0
-q
-2q
...
Erros
de
quantização 0 T 2T 3T ...
Tempo ou espaço

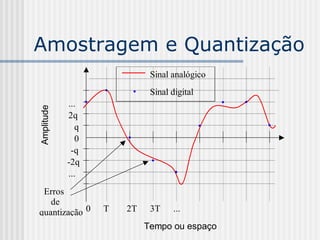
68. Amostragem e Quantização
- Parâmetros
 T: período de amostragem (unidade de
espaço ou tempo)
 f = 1/T: freqüência de amostragem
(amostras/unidade de espaço ou tempo)
 q: passo de quantização
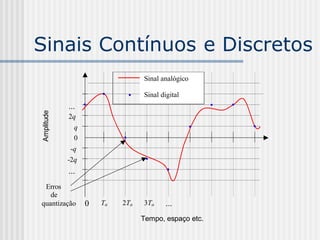
 Sinal analógico: s(t), s(x)
 Sinal digitalizado: s[nT], n inteiro não
negativo, s[nT] {-Mq, ..., -2q, -q, 0, q,
2q, ..., (M-1)q}

69. Amostragem e Quantização
– Exemplo 1
 Sinal analógico s(t): voltagem de
saída de um sistema elétrico em
função do tempo
40
20
Sinal analógico
Volts
0
-20
-40
0 1 2 3 4 5 6 7
segundos

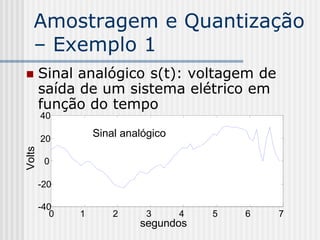
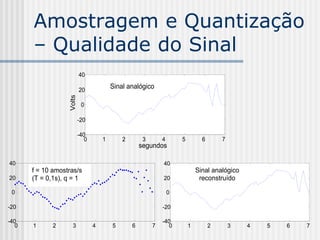
70. Amostragem e Quantização
– Exemplo 1
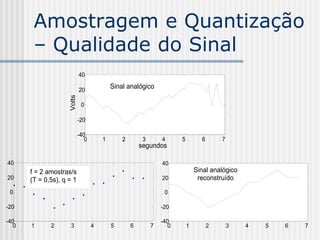
 T = 0.5s, q = 0.5V, M = 64: s[0.5.n], n =
0, 1, 2, ...
 s[0.5n]  {-32, -31.5..., -0.5, 0, 0.5
1,...,31, 31.5}
 s[0]=9.5V,s[0.5]=8V,s[1]=-2V, s[1.5]=
-10.5V, ...
 Notação Simplificada:
 s[n]  {-M,..., -2, -1, 0, 1, 2,..., M-1}
 s[0]=19, s[1]=16, s[2]=-4, s[3]=-21,...
 s[n] = {19, 16, -4, -21, ...}

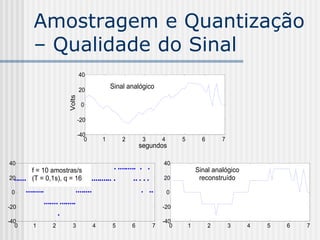
71. Amostragem e Quantização
– Exemplo 2
 Em um processo de digitalização foram colhidas
N=10 amostras de um sinal de temperatura
(graus Celsius) igualmente espaçadas ao longo de
um segmento de reta unindo duas cidades A e B.
A primeira amostra foi colhida na cidade A e a
última na cidade B. O sinal digital resultante é
s[n] = {12 12 13 13 14 13 14 14 15 14}
 Perguntas:
(a) Distância entre as cidades?
(b) Valores de temperatura registrados?
(c) Limites de temperatura registrável?
(d) Qual o valor de s[5km]?

72. Amostragem e Quantização
– Solução do Exemplo 2
 Precisamos conhecer f, q e M!
 Dados:
f = 0.1 amostra/km
q = 2o Celsius
M = 16;

73. Amostragem e Quantização
– Solução do Exemplo 2
 T = 10 km/amostra
 (a) Distância entre as cidades =
(10-1)x10 = 90km
 (b) Temperaturas em graus Celsius:
{24 24 26 26 28 26 28 28 28 30}
 (c) Limites de temperatura em graus
Celsius: [-32, 30]
 (d) s[5km]: no sinal digital s[nT] não há
nT = 5km!

74. Conversores Analógico-
Digitais (ADC)
 Conversor Analógico/Digital (Analog to
Digital Converter - ADC): amostra,
quantiza em L níveis e codifica em binário.
 Um transdutor deve converter o sinal de
entrada para tensão elétrica (V)
 Códigos de b bits: L = 2b níveis de
quantização
 Exemplo: b = 8, L = 256
 ADC de b bits

75. Conversores Analógico-
Digitais (ADC)
 ADC unipolar: voltagem de entrada de 0 a Vref
 ADC bipolar: voltagem de entrada de -Vref a
Vref
 Exemplo: ADC unipolar de 3 bits, Vref = 10 V
 L = 23 = 8, Resolução de voltagem: 10/8 = 1,25V
 Exemplo: ADC bipolar de 3 bits, Vref = 5 V
 L = 23 = 8, Resolução de voltagem: 10/8 = 1,25V

76. ADC
Unipolar Bipolar
Voltagem Código Voltagem Código
[0,00, 1,25) 000 [-5,0, -3,75) 000
[1,25, 2,50) 001 [-3,75, -2,5) 001
[2,50, 3,75) 010 [-2,5, -1,25) 010
[3,75, 5,00) 011 [-1,25, 0,0) 011
[5,00, 6,25) 100 [0,00, 1,25) 100
[6,25, 7,50) 101 [1,25, 2,50) 101
[7,50, 8,75) 110 [2,50, 3,75) 110
[8,75, 10,0) 111 [3,75, 5,00) 111

77. Conversores Analógico-
Digitais (ADC)
 O bit menos significativo (LSB) do código
se altera em incrementos de 1,25V.
 Resolução de voltagem: “valor” do LSB
 Alguns parâmetros: fa, Vref, b, ...

78. Amostragem e Quantização
– Qualidade do Sinal
40
20
Sinal analógico
Volts
0
-20
-40
0 1 2 3 4 5 6 7
segundos
40 40
f = 2 amostras/s Sinal analógico
20 (T = 0,5s), q = 1 20 reconstruído
0 0
-20 -20
-40 -40
0 1 2 3 4 5 6 7 0 1 2 3 4 5 6 7

79. Amostragem e Quantização
– Qualidade do Sinal
40
20
Sinal analógico
Volts
0
-20
-40
0 1 2 3 4 5 6 7
segundos
40 f = 5 amostras/s 40
Sinal analógico
(T = 0,2s), q = 1
20 20 reconstruído
0 0
-20 -20
-40 -40
0 1 2 3 4 5 6 7 0 1 2 3 4 5 6 7

80. Amostragem e Quantização
– Qualidade do Sinal
40
20
Sinal analógico
Volts
0
-20
-40
0 1 2 3 4 5 6 7
segundos
40 40
f = 10 amostras/s Sinal analógico
20 (T = 0,1s), q = 1 20 reconstruído
0 0
-20 -20
-40 -40
0 1 2 3 4 5 6 7 0 1 2 3 4 5 6 7

81. Amostragem e Quantização
– Qualidade do Sinal
40
20
Sinal analógico
Volts
0
-20
-40
0 1 2 3 4 5 6 7
segundos
40 40
f = 10 amostras/s Sinal analógico
20 (T = 0,1s), q = 16 20 reconstruído
0 0
-20 -20
-40 -40
0 1 2 3 4 5 6 7 0 1 2 3 4 5 6 7

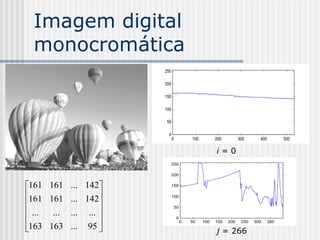
82. Notação simplificada para
Imagens
 f[i, j]  {0, 1, 2,..., M-1}
 Tipicamente, M = 256

83. Imagem digital
monocromática
250
200
150
100
50
0
0 100 200 300 400 500
i=0
250
200
161 161 ... 142 150
161 161 ... 142 100
  50
 ... ... ... ... 
 
0
0 50 100 150 200 250 300 350
163 163 ... 95 
j = 266

84. Resolução Espacial e de
Contraste
256x256 / 256 níveis 256x256 / 64 níveis 256x256 / 2 níveis
32x32 / 256 níveis

85. Imagens RGB
Banda R Banda G Banda B
Imagem RGB

86. Imagens Digitais
 Uma imagem é uma matriz bidimensional
observada de forma pictórica.
 Imagens de densidade demográfica, de
raios x, de infravermelho, de
temperaturas de uma área, etc.

87. Scanners
 Monocromáticos: fila de diodos
fotossensíveis em um suporte que se
desloca
 Coloridos: fila de diodos fotossensíveis,
recobertos por filtros R, G e B, em um
suporte que se desloca
 Lâmpada fluorescente branca
ilumina o objeto
 Diodos produzem carga elétrica
proporcional à intensidade da
luz refletida pelo objeto

88. Scanners

89. Scanners
 Th: distância entre diodos no suporte
 Tv: tamanho do passo do suporte
 Th e Tv definem a resolução espacial
 M: profundidade de cor ou resolução de
contraste
 Resolução espacial: pontos por polegada
(dot per inch, dpi) (1 ponto = 1 sensor em
scanner monocromático, 3 sensores em
scanners RGB)
 1 pol = 2,54 cm.

90. Scanners
 Ex: 300 x 300 dpi, digitalização de formato
carta(8,5 x 11’’), no máximo
 8,5x300=2550 diodos (mono) ou
 3x2550=7650 diodos (cor)
 Aumentar resolução vertical sem aumentar
o número de sensores

91. Scanners
N pontos/polegada
Movimento do braço:
... M passos/polegada

92. Câmeras Digitais

93. Câmeras Digitais
 Sensor de imagem:
matriz de diodos
fotosensíveis cobertos
por filtros R, G e B
 Diodos produzem carga
elétrica proporcional à
intensidade da luz
refletida pelo objeto
 Resolução espacial de câmeras: número de
pontos (ou pixels), RxC (1 ponto = 3 sensores)

94. Câmeras Digitais
...
...

95. Qualidade dos Sensores
 S9500 – ISO 1600  EOS350D – ISO 1600

96. Qualidade dos Sensores
 EOS350D – ISO 1600
 S9500 – ISO 1600

97. Câmeras Digitais
 Exemplo: Sony DSC V1: 1944 x 2592 pixels =
5Mpixels. Digitalizar papel em formato carta com
imagem da folha ocupando todo o sensor.
Resolução (em dpi)? Comparar com scanner de
300 x 300 dpi, em qualidade, número de
sensores e preço. Comparar com scanner de
2400 x 2400 dpi.

98. Câmeras Digitais
 Solução:
 1944 / 8,5 pol x 2592/11 pol = 228,7 dpi x =
235,6 dpi
 Resolução espacial inferior à do scanner de
300 x 300 dpi, com 1944 x 2592 x 3 / 7650 =
1976 vezes mais sensores, 10 a 20 vezes mais
caro, aberrações geométricas e de cor, etc.
 Câmeras digitais têm escopo de aplicação
maior e são mais rápidas
 Scanner de 2400 x 2400 dpi = câmera de 500
Mpixels!

99. Dispositivos Gráficos
 Exemplo: câmera digital, 3000 x 2000
pontos (6 Mpixels), impressa em formato
15x10 cm, com o mesmo no. de pontos.
Qual a resolução (dpi) no papel?

100. Dispositivos Gráficos
 Exemplo: câmera digital, 3000 x 2000
pontos (6 Mpixels). Imprimir em formato
15x10 cm, com o mesmo no. de pontos.
Qual a resolução (dpi) no papel?
 15x10 cm = 3,94 x 5,91 pol.
 Resolução (dpi): 3000/5,91 = 2000/3,94 =
507x507 dpi

101. Dispositivos Gráficos
 Ex: foto 10x15cm, scanneada a 1200x1200
dpi, 24 bits/pixel. Tamanho em bytes?
 Dimensões impressa em 1440x1440 dpi?
 Dimensões impressa em 720 x 720 dpi?
 Dimensões em tela de 14 pol., resolução
1024x768? Resolução em dpi da tela?
 Dimensões em tela de 17 pol., resolução
1024x768? Resolução em dpi da tela?

102. Dispositivos Gráficos
 Solução:
 Foto 10x15cm = 3,94 x 5,91 pol.
 Tamanho em bytes: 3,94x1200 x
5,91x1200 pixels x 3 bytes/pixel = 4728 x
7092 x 3 = 100 milhões de bytes (96 MB)
 Dimensões (pol) em impressora de
1440x1440 dpi: 4728/1440 x 7092/1440 =
3,3 x 4,9 pol.
 Dimensões (pol.) em impressora de 720 x
720 dpi = 6,6 x 9,9 pol

103. Dispositivos Gráficos
 Solução:
 Dimensões em tela de 14 pol., em resolução de
1024x768 pontos? Resolução em dpi da tela?
x2 + y2 = 142
x/y = 3/4
x = 8,4 pol; y = 11,2 pol.
 Res. = 1024/11,2 x 768/8,4 = 91,4 x 91,4 dpi.
 Dimensões = 4728 / 91,4 x 7092 / 91,4 =51,73 x
77,59 pol = 131,39 x 197,09cm (apenas parte da
imagem será visível)

104. Dispositivos Gráficos
 Solução:
 Dimensões em tela de 17 pol., em resolução de
1024x768 pontos? Resolução em dpi da tela?
y = 13,6 pol; x = 10,2 pol
 Res. = 1024/13,6 x 768/10,2 = 75,3 x 75, 3 dpi
(pior que no monitor de 14 pol)
 Dimensões = 4728 / 75,3,4 x 7092 / 75,3 =62,79
x 94,18 pol = 159,49 x 239,22cm (apenas parte da
imagem será visível)

105. Monitor CRT
 A e C: Placas aceleradoras e defletoras
 D: tela com pontos de fósforos RGB
 F: Máscara de sombra ou grade de abertura

106. Monitor CRT

107. Monitor RGB

108. Monitor RGB
Linha 0
Linha 1
Linha R-1

109. Operações com Imagens
 Espaço / freqüência
 Locais / pontuais
 Unárias / binárias / ... / n-árias

110. Operações n-árias
 Operação T sobre n imagens, f1, f2, ..., fn,
produzindo imagem de saída g
g = T[f1, f2, ..., fn]
 Operações binárias: n = 2
 Operações unárias ou filtros: n = 1
g = T[f]

111. Operações Pontuais
 g(i, j) depende do valor do pixel em (i’, j’)
das imagens de entrada
 Se (i, j) = (i’, j’) e operação unária:s = T(r)
r, s: nível de cinza de f e g em (i, j)
s s
(0,0) m r (0,0) m r

112. Operações Pontuais
s s
L-1
L-1
(r2, s2)
(r1, s1)
(0,0) (0,0) r
L-1 r L-1

113. Operações Locais
 g(i, j) depende dos valores dos pixels das
imagens de entrada em uma vizinhança
de (i’, j’)
f g
j j
i i
Vizinhança de (i, j)

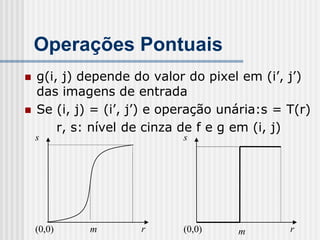
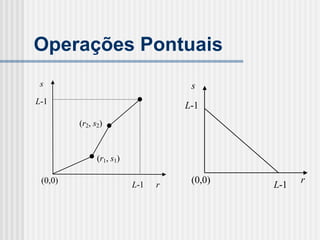
114. Operações Locais
 Exemplo: Filtro “Média”
1
g (i, j )  [ f (i  1, j  1)  f (i  1, j )  f (i  1, j  1) 
9
 f (i, j  1)  f (i, j )  f (i, j  1) 
 f (i  1, j  1)  f (i  1, j )  f (i  1, j  1)]
 Operação sobre pixels da imagem
original: resultado do filtro em um dado
pixel não altera o resultado em outros
pixels.
 Primeira e última coluna/linha?

115. Filtros de suavização
 Média, Moda, Mediana, Gaussiano...
 Vizinhança m x n

116. Photoshop!

117. Photoshop!

118. Photoshop!

119. Photoshop!

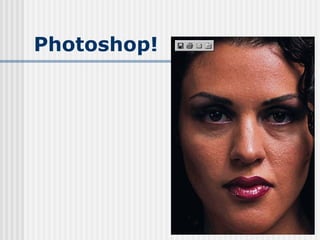
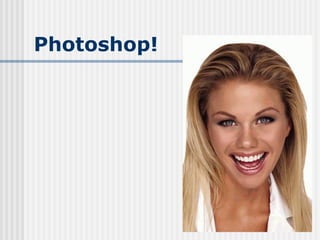
120. Filtros de aguçamento e
detecção de bordas
 Efeito contrário ao de suavização: acentuam
variações de intensidade entre pixels
adjacentes.
 Baseados no gradiente de funções
bidimensionais.
 Gradiente de f(x, y):
 f 
 x   f
2 2 1 / 2
     f 
G[f(x, y)] = G[ f ( x, y )]       
 y 
   x    
 f   
 
 y 

121. Filtros de detecção de bordas
 g(i, j): aproximação discreta do módulo do
vetor gradiente em f(i, j).
 Aproximações usuais:
g(i, j) = {[f(i,j)-f(i+1,j)]2 + [f(i,j)-f(i,j+1)]2}1/2
g(i, j) = |f(i,j)-f(i+1,j)| + |f(i,j)-f(i,j+1)|
Gradiente de Roberts:
g(i,j) = {[f(i,j)-f(i+1,j+1)]2+[f(i+1,j)-f(i,j+1)]2}1/2
g(i, j) = |f(i,j)-f(i+1,j+1)| + |f(i+1,j)-f(i,j+1)|

122. Filtros de detecção de bordas
Gradiente de Prewitt:
g(i, j) = |f(i+1,j-1) + f(i+1, j) + f(i+1, j+1)
- f(i-1, j-1) - f(i-1, j) - f(i-1, j+1)|
+|f(i-1, j+1) + f(i, j+1) + f(i+1, j+1)
- f(i-1, j-1) - f(i, j-1) - f(i+1, j-1)|
Gradiente de Sobel:
g(i, j) = |f(i+1, j-1) + 2f(i+1, j) + f(i+1, j+1)
- f(i-1, j-1) - 2f(i-1, j) - f(i-1, j+1)|
+ |f(i-1, j+1) + f(i, j+1) + f(i+1, j+1)
- f(i-1, j-1) - 2f(i, j-1) - f(i+1, j-1)|

123. Gradiente de Roberts
Limiares 15, 30 e 60

124. Processamento de
Histograma
 Se o nível de cinza l ocorre nl vezes em
imagem com n pixels, então
nl
P(l ) 
n
 Histograma da imagem é uma
representação gráfica de nl ou P(l)

125. Histograma
Histograma
nl
Imagem 7
6
1 0 0 3 3 5
4
0 0 3 3 3
3
1 1 1 3 3 2
1
0
0 1 2 3 l
Imagem 3 x 5 (L = 4) e seu histograma

126. Histograma
 O histograma representa a distribuição
estatística de níveis de cinza de uma imagem
nl nl nl
0 255 l 0 255 l 0 255 l

127. Histograma
10000
8000
6000
4000
2000
0
0 50 100 150 200 250

128. Histograma
1500
1000
500
0
0 50 100 150 200 250

129. Expansão de Histograma
 Quando uma faixa reduzida de níveis de
cinza é utilizada, a expansão de
histograma pode produzir uma imagem
mais rica.
nl nl nl
A B C
l l l
m0=0 m1 L-1 0 m0 m1 L-1 0 m0 m1=L-1

130. Expansão de Histograma
 Quando uma faixa reduzida de níveis de
cinza é utilizada, a expansão de
histograma pode produzir uma imagem
mais rica:
 r  rmin 
s  T ( r )  round 
r ( L  1) 

 max  rmin 

131. Expansão de Histograma
1500
1000
500
0
0 50 100 150 200 250
1500
1000
500
0
0 50 100 150 200 250

132. Expansão de Histograma
 Expansão é ineficaz nos seguintes casos:
nl nl nl
A B C
l l l
0 L-1 L-1 0 m0 m1 L-1 0 L-1

133. Equalização de Histograma
 Se a imagem apresenta pixels de valor 0
e L-1 (ou próximos a esses extremos) a
expansão de histograma é ineficaz.
 Nestas situações a equalização de
histograma pode produzir bons
resultados.
 O objetivo da equalização de histograma
é gerar uma imagem com uma
distribuição de níveis de cinza uniforme.

134. Equalização de Histograma
 L 1 r 
s  T (r )  round   nl 
 RC l 0 
1500
1000
500
0
0 50 100 150 200 250
1500
1000
500
0
0 50 100 150 200 250

135. Equalização de Histograma
 Exemplo: imagem 64 x 64, L = 8
nl
l nl
0 790 1200
1 1023 1000
2 850 800
3 656 600
4 329
400
5 245
200
6 122
0
7 81 0 1 2 3 4 5 6 7 l

136. Equalização de Histograma
 Exemplo (cont.):
 r=0s = round(790 x 7 / 4096) = 1
 r=1s = round(1813 x 7 / 4096) = 3
 r=2s = round(2663 x 7 / 4096) = 5
 r=3s = round(3319 x 7 / 4096) = 6
 r=4s = round(3648 x 7 / 4096) = 6
 r=5s = round(3893 x 7 / 4096) = 7
 r=6s = round(4015 x 7 / 4096) = 7
 r=7s = round(4096 x 7 / 4096) = 7

137. Equalização de Histograma
 Exemplo: imagem 64 x 64, L = 8
l nl nk
0 0
1 790 1200
1000
2 0
800
3 1023
600
4 0
400
5 850
200
6 985
0
7 448 0 1 2 3 4 5 6 7 k

138. Equalização de Histograma
nl Hist. Original nl Hist. Equal. (Ideal) nl Hist. Equal. (Real)
0 L-1 L-1 l 0 m0 m1 L-1 l 0 L-1 l

139. Equalização de Histograma
 Expansão de histograma é pontual ou
local? E equalização de histograma?
 O que ocorre quando uma imagem com
um único nível passa pela operação de
equalização de histograma?
 Melhor fazer equalização seguido por
expansão de histograma, o inverso, ou a
ordem não importa?

140. Equalização de Histograma
Local
 Para cada locação (i,j) de f
• Calcular histograma na vizinhança de
(i,j)
• Calcular s = T(r) para equalização de
histograma na vizinhança
• G(i,j) = s

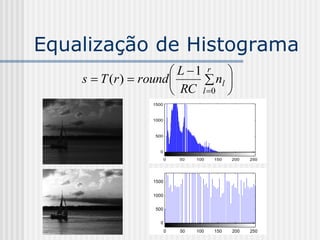
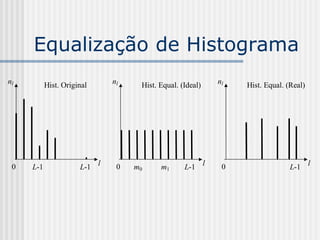
141. Controle de contraste
adaptativo
 c
 (i, j )  [ f (i, j )   (i, j )]; (i, j )  0
g (i, j )    (i, j )
 f (i, j ); (i, j )  0


142. Controle de contraste
adaptativo

143. Filtros baseados na função
gaussiana
 Função gaussiana:
 Derivada:
 Derivada segunda:

144. Filtros baseados na função
gaussiana
 Gaussiana, derivada e derivada
segunda

145. Filtros baseados na função
gaussiana
 A máscara é construída pela
amostragem de G(x), G’(x) e G’’(x)
 x = -5σ, ...-2, -1, 0, 1, 2..., 5σ

146. Filtros gaussianos
bidimensionais
Com r = sqrt(x2 + y2)

147. Pseudo-cor
Nível de R G B
cinza
0 15 20 30
1 15 25 40
...
L-1 200 0 0

148. Outros filtros:
 Curtose, máximo, mínimo etc.
 Filtros de suavização + filtros de
aguçamento
 Laplaciano do Gaussiano (LoG)
 “Emboss”
 Aumento de saturação
 Correção de gama
 ...

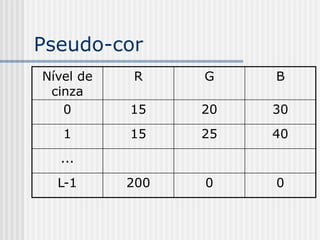
149. Filtros Lineares e Invariantes
ao Deslocamento
 Filtro linear:
T [af1 + bf2] = aT [f1] + bT [f2]
para constantes arbitrárias a e b.
 Filtro invariante ao deslocamento:
Se g[i, j] = T [f[i, j]]
então g[i - a, j – b] = T [f[i - a, j – b]].
 Se i e j são coordenadas espaciais: filtros
espacialmente invariantes.

150. Convolução
 Convolução de s(t) e h(t):

g (t )  s (t ) * h (t )   s( )h(t   )d


151. Convolução

g (t )  s (t ) * h (t )   s( )h(t   )d
 h ( )
s(t)
t3 
(0,0)
t0 t1 t 0 t2
h (t   )
h (  )
-t3 -t2 0  
-t3+t -t2+t

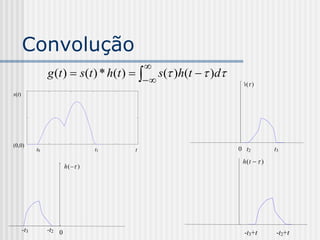
152. Convolução
 Observe que g(t) = 0 para
t  [t0  t2 , t1  t3 ]

153. Convolução Discreta Linear
 Convolução linear entre s[n] e h[n]

g[n]  s[n ] * h[n]   s[ ]h[n   ]
  
 Se s[n] e h[n] têm N0 e N1 amostras,
respectivamente => extensão com zeros:
N 1
g[n]  s[n] * h[n]   s[ ]h[n   ]
 0
com N = N0 + N1 – 1.

154. Convolução Discreta Linear
6 s ( ) 6 h ( )
4 4
2 2
0 1 2 3 4 5 
6 0 1 2 3 4 5 
6 h (  ) 6 h(n   )
4 4
2 2

-5 -4 -3 -2 -1 0 1 n 

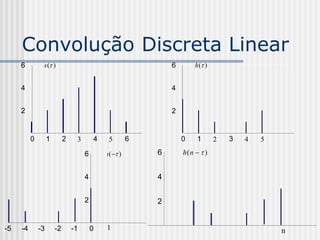
155. Convolução Discreta Linear
6 s ( )
4
2
0 1 2 3 4 5 
6
6 h (  )
4
 g[0] = 3
2
-5 -4 -3 -2 -1 0 1 

156. Convolução Discreta Linear
6 s ( )
4
2
0 1 2 3 4 5 
6
6 h (1   )
4
 g[0] = 3
2

 g[1] = 8
-5 -4 -3 -2 -1 0 1

157. Convolução Discreta Linear
6 s[n] 6 h[n]
4 4
2 2
0 1 2 3 4 5 6 n 0 1 2 3 4 5 n
30 g[n] = s[n]* h[n]
20
10
0 1 2 3 4 5 6 7 8 9 10 11 n

158. Convolução Discreta Linear
s[n] Filtro g[n]
h[n]

g[n]  s[n ] * h[n]   s[ ]h[n   ]
  

159. Impulso Unitário
 Delta de Dirac ou (t)
impulso unitário 1
contínuo
 Duração = 0
 Área = 1 0 t
[n]
 Delta de Kronecker
ou impulso unitário 1
discreto
0 n

160. Sinais = somatório de
impulsos
 Delta de Kronecker A[n-n0]
A
0 n0 n
s[n]  s[0] [n]  s[1] [n  1]  .... s[ N  1] [n  ( N  1)]
N 1
s[n]   s[ ] [n   ]
 0

161. Resposta ao impulso
 Resposta de um filtro a s[n]:
N 1 N 1
g[ n]   s[ ]h[n   ]   h[ ]s[n   ]
 0  0
 Resposta de um filtro ao impulso
N 1 N 1
g[ n]   [ ]h[n  ]   [n   ]h[ ]
 0  0
N 1
h[n]   [n   ]h[ ]
 0

162. Resposta ao impulso
 h[n]:
 Resposta ao impulso
 Máscara convolucional
 Kernel do filtro
 Vetor de coeficientes do filtro

163. Filtros FIR
 Finite Impulse Response
N 1
y[n]   ak x[n  k ]
k 0
ak  h[k ]

164. Filtros IIR
 Infinite Impulse Response
N 1 M 1
y[n]   ak x[n  k ]   bk y[n  k ]
k 0 k 1
 Filtros recursivos

165. Filtros IIR (exemplo)
 Encontre a resposta ao impulso do
seguinte sistema recursivo. Supor que o
sistema está originalmente relaxado (y[n]
= 0 para n < 0)
y[n] = x[n] - x[n-1] – 0,5y[n-1]

166. Filtros IIR (exemplo)
 Exemplo:
 y[n] = x[n] - x[n-1] – 0,5y[n-1]
 y[0] = delta[0]–delta[-1]–0,5y[-1] = 1
 y[1] = delta[1]–delta[0]–0,5y[0] = -1,5
 y[2] = delta[2]–delta[1]–0,5y[1] = 0,75
 y[3]= delta[3]–delta[2]–0,5y[2] = -0,325
 y[n] = -0,5y[n-1], n > 1

167. Filtros IIR (exemplo 2)
 Exemplo: encontre a resposta ao impulso
do seguinte sistema recursivo. Supor que
o sistema está originalmente relaxado
(y[n] = 0 para n < 0)
y[n] - y[n-1] = x[n] - x[n-4]

168. Filtros IIR (exemplo 2)
 Exemplo (Solução)
 y[n] = y[n-1] + x[n] - x[n-4]
 y[0] = y[-1] + delta[0] - delta[-4] = 1
 y[1] = y[0] + delta[1] - delta[-3] = 1
 y[2] = y[1] + delta[2] - delta[-2] = 1
 y[3] = y[2] + delta[3] - delta[-1] = 1
 y[4] = y[3] + delta[4] - delta[0] = 0
 y[5] = y[4] + delta[5] - delta[1] = 0
 y[6] = y[7] = ... = 0

169. Convolução Discreta Circular
 Sinais s[n] e h[n] com N0 e N1 amostras,
respectivamente => extensão com zeros:
s[n ], 0  n  N 0 h[n ], 0  n  N1
s e [n ]   he [n ]  
0, N 0  n  N 0, N1  n  N
 Extensão periódica: considera-se que
se[n] e he[n] são períodos de sp[n] e hp[n]
 Convolução circular:
N 1
g p [n]  s[n]  h[n]   s p [ ]h p [n   ]
 0

170. Convolução Circular x Linear
 Fazendo-se N = N0 + N1 – 1
s[n]  h[n]  s[n] * h[n]

171. Convolução de Imagens
 f[i, j] (R0xC0) e h[i, j] (R1xC1): extensão
por zeros
R 1 C 1
g[i, j ]  f [i, j ] * h[i, j ]    f [ ,  ]h[i   , j   ]
 0  0
R 1 C 1
g p [i, j ]  f [i, j ]  h[i, j ]    f p [ ,  ]h p [i   , j   ]
 0   0
 Iguais se R=R0+R1–1 e C=C0+C1–1

172. Máscaras Convolucionais
1 1 1 1 0 -1 -1 -1 -1
0 0 0 1 0 -1 -1 8 -1
-1 -1 -1 1 0 -1 -1 -1 -1
1/9 1/9 1/9 0.025 0.1 0.025
1/9 1/9 1/9 0.1 0.5 0.1
1/9 1/9 1/9 0.025 0.1 0.025

173. Operador de Bordas de
Kirsch
5 5 5 -3 5 5 -3 -3 5
-3 0 -3 -3 0 5 -3 0 5
-3 -3 -3 -3 -3 -3 -3 -3 5
-3 -3 -3 -3 -3 -3 ...
-3 0 5 -3 0 -3
-3 5 5 5 5 5
 Filtragem sucessiva com cada máscara
 Pixel de saída recebe o valor máximo

174. Máscaras Convolucionais
 Em geral:
 Máscaras de integração somam
para 1
 Máscaras de diferenciação somam
para 0

175. Transformada z
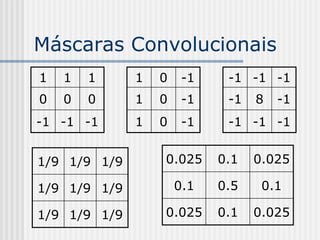
 Transformada z de x[n]:

Z{x[n]}  X [ z ]   x[n] z  n
n 
 z: variável complexa

176. Propriedades da
Transformada z
 Linearidade: Se x[n] = ax1[n] + bx2[n],
(a e b: constantes arbitrárias), então:
X [ z]  aX1[ z]  bX 2 [ z]

177. Propriedades da
Transformada z
 Deslocamento:
Z{x[n+k]} = zkX[z], k inteiro
 Prova: 
Z{x[n  k ]}   x[n  k ]z  n
n  
 Fazendo m = n+k:
 
Z{x[n  k ]}   x[m]z  (n  k )  z k  x[m]z  n  z k X [ z ]
m   m  

178. Propriedades da
Transformada z
 Convolução:

y[n]  h[n] * x[n]   h[k ]x[n  k ]  Y [ z]  H [ z] X [ z]
k  
 Se h[n] é a resposta ao impulso de
um filtro, H[z] é a função de
transferência do filtro

179. Propriedades da
Transformada z
 Convolução (Prova)
    n
Z{h[n] * x[n]}     h[k ]x[n  k ] z
n   k  
 

 
   h[k ]x[n  k ]z  n
k   n  
 
  h[k ]z  k  x[n]z  n
k   n  
 H [ z] X [ z]

180. Função de Transferência
 Equação de diferenças de um filtro
N 1 M 1
y[n]   ak x[n  k ]   bk y[n  k ]
k 0 k 1
M 1 N 1
 bk y[n  k ]   ak x[n  k ]
k 0 k 0
b0  1

181. Função de Transferência
 Transformada Z da Equação de
diferenças
M 1
 
  N 1
 

Z   bk y[n  k ]  Z   a k x[n  k ]
 k 0
 
  k 0
 

M 1 N 1
 bk Z{ y[n  k ]}   ak Z{ x[n  k ]}
k 0 k 0
M 1 N 1
 bk z  k Y [ z ]   ak z  k X [z ]
k 0 k 0

182. Função de Transferência
 Aplicando a transformada z em
ambos os lados e simplificando:
N 1
 ak z  k
Y [ z] k 0
H [ z]  
X [ z] M 1
1  bk z  k
k 1
 Pólos: raízes do denominador
 Zeros: raízes do numerador
 Pólos e zeros: estabilidade

183. Função de Transferência
 BIBO: Bounded-input, bounded-
output
 Sistemas BIBO-estáveis: sistemas
causais tais que:

 | h[k ] |  
k 0

184. Estimação da Resposta em
Freqüência
 Resposta em freq. a partir de H[z]

H [ z]   h[n]z  n
n  

H [ e j ]   h[n]e  jn , 0    2
n  
 Comparar com
N 1 j 2un
1 
F [u ] 
N
 s[n]e N
n 0

185. Estimação da Resposta em
Freqüência
 Exemplo: encontre a resposta em
freqüência do filtro y[n] = (x[n] + x[n-1])/2
utilizando a transformada Z
Y[z] = (X[z] + z-1X[z] )/2 = X[z](1+z-1)/2
H[z] = (1+z-1)/2
H[ejw] = (1+e-jw)/2 = e-jw/2 (ejw/2 + e-jw/2)/2 =
e-jw/2cos(w/2)
 |H[ejw]| = cos(w/2), -pi< w < pi

186. Estimação da Resposta em
Freqüência
 Exemplo: encontre a resposta em
freqüência do filtro y[n] = (x[n] - x[n-1])/2
utilizando a transformada Z
Y[z] = (X[z] - z-1X[z] )/2 = X[z](1-z-1)/2
H[z] = (1-z-1)/2
H[ejw] = (1-e-jw)/2 = e-jw/2 (ejw/2 - e-jw/2)/2 =
je-jw/2sen(w/2)
 |H[ejw]| = |sen(w/2)|, -pi< w < pi

187. Correlação
 Convolução: 
g[n]  s[n ] * h[n]   s[ ]h[n   ]
  
 Correlação:

g[n]  s[n]  h[n]   s[ ]h[  n]
  
 Quando um dos sinais é par,
correlação = convolução

188. Correlação
 Exemplo:
h[-1] = 3; h[0] = 7; h[1] = 5;
s[0..15] = {3, 2, 4, 1, 3, 8, 4, 0, 3, 8, 0,
7, 7, 7, 1, 2}
 Extensão com zeros

189. Correlação
 Exemplo:
g[1]  s[0]h[1]  15
1
g[0]   s[ ]h[ ]  s[0]h[0]  s[1]h[1]  31
 0
2
g[1]   s[ ]h[  1]  s[0]h[1]  s[1]h[0]  s[2]h[1]  43
 0
3
g[2]   s[ ]h[  2]  s[1]h[1]  s[2]h[0]  s[3]h[1]  39
 1
...

190. Correlação
 Exemplo:
g[0..15] = 31, 43, 39, 34, 64, 85, 52, 27,
61, 65, 59, 84, 105, 75, 38, 27
 Observe que g[5] é elevado, pois é
obtido centrando h em s[5] e calculando
a correlação entre (3, 7, 5) e (3, 8, 4)
 Mas g[12] é ainda maior, devido aos
valores elevados de s[11..13]

191. Correlação Normalizada
 A correlação normalizada elimina a
dependência dos valores absolutos
dos sinais:

 s[ ]h[  n]
g[n]  s[n]  h[n]    
 
 ( s[ ]) 2  (h[  n]) 2
     

192. Correlação Normalizada
 Resultado para o exemplo anterior:
 g[0..15] = .??? .877 .934 .73 .81
.989 .64 .59 .78 .835 .61 .931 .95
.83 .57 .???
 Valor máximo: g[5]

193. Detecção e estimação
Fonte:
http://www.dspguide.com/ch7/3.htm

194. Detecção e estimação
 Gaivota, “filtro casado” (olho) e
imagem de correlação normalizada
(máximo no olho)
Fonte: http://www.dca.fee.unicamp.br/dipcourse/html-dip/c6/s5/front-page.html

195. Estimação Espectral
 O cálculo direto do espectro de
amplitudes e fases não é fidedigno
 O espectro pode variar muito em
diferentes seções de um mesmo sinal.
 Variância é um indicador de qualidade
 O problema pode ser causado por ruído,
escassez de dados, comportamento não
estacionário etc.

196. Periodograma
 O quadrado do módulo do espectro de
amplitudes: densidade espectral de
potência (PSD), ou espectro de potência
 Periodograma: dividir sinal em K seções
adjacentes (com ou sem intersecção) de
mesmo tamanho; obter PSD de cada
seção; obter média das PSDs
 Variância se reduz por fator K1/2
 Resolução espectral diminui

197. Janelamento (windowing)
 Todo sinal discreto obtido a partir de um
sinal analógico é resultado da
multiplicação de um sinal discreto de
duração infinita por um pulso, ou janela,
retangular:
1 0  n  N
wn  
0 caso contrário

198. Janelamento (windowing)
 A janela retangular pode gerar grandes
descontinuidades na forma de onda
original

199. Janelamento (windowing)
 Multiplicação no tempo equivale a
convolução na freqüência (Fourier)
 DFT da janela retangular: função sinc
(sine cardinal, kernel de Dirichlet, função
de amostragem):
1 x0

sinc( x)   sen x
 x caso contrário


200. Janelamento (windowing)
 A convolução com um sinc introduz
distorções no espectro
 Janelas mais “suaves” reduzem estas
distorções, mas distorcem mais as
amostras centrais-> Compromisso
 Dezenas dessas janelas tem sido
avaliadas e utilizadas em diversas
aplicações

201. Janela de Hamming
  2n 
0,54  0,46 cos  0nN
wn    N 1
0 caso contrário


202. Janela de Hamming
 Seno multiplicado por janela retangular e
de Hamming

203. Janela de Hamming
 DFT de seno multiplicado por janela
retangular e de Hamming

204. Outras Janelas
 Blackman-Harris, Dolph-Chebyshev,
Kaiser-Bessel (superiores?)
 Tukey, Poisson, Hanning etc

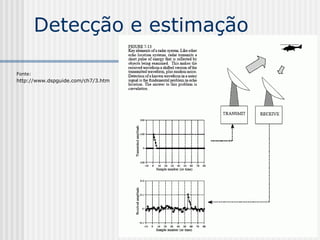
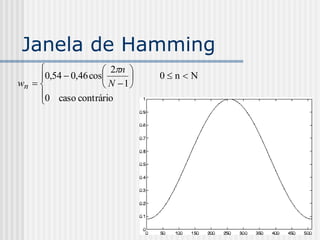
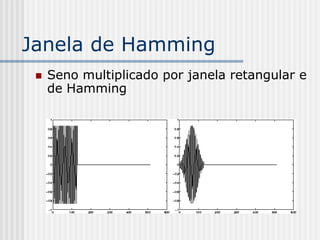
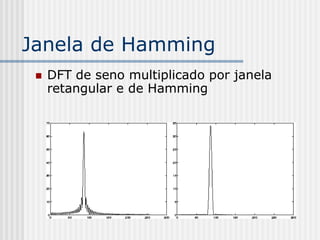
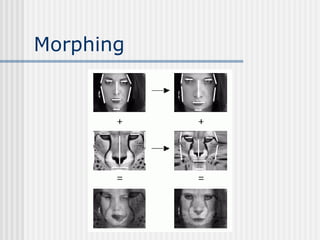
205. Dissolve Cruzado
 ht (i, j)= (1 - t) f(i, j) + t g(i, j)
 t é um escalar no intervalo [0, 1]

206. Dissolve Cruzado
t = 0,3 t = 0,5 t = 0,7

207. Dissolve Cruzado Não-
Uniforme
 ht(i, j)= [1 - t(i, j)] f(i, j) + t(i, j) g(i, j)
 t é uma matriz com as mesmas
dimensões de f e g cujos elementos
assumem valores no intervalo [0, 1]

208. Dissolve Cruzado Não-
Uniforme
t(i,j)=(i+j)/(R+C-2) t(i,j)=j/(C-1) t(i,j)=i/(R-1)

209. Detecção de Movimento
L  1, se | f1  f 2 | Lt
g
0, caso contrario
f1 f2 g

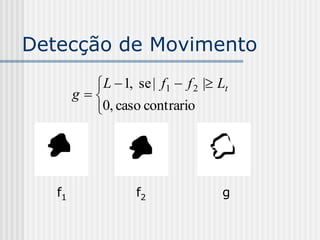
210. Redução de Ruído por Média
de Imagens
 f[i, j] imagem sem ruído
 nk(i, j) ruído de média m
 gk[i,j] = f[i,j] + nk(i,j)
M

1
g [i, j ]  g k [i, j ]
M k 1

211. Redução de Ruído por Média
de Imagens
M

1
g [i, j ]  ( f [i, j ]  nk (i, j ))
M k 1
M

1
g [i, j ]  f [i, j ]  nk (i, j )
M k 1
 Para M grande:
g[i, j ]  f [i, j ]  m

212. Operações Topológicas
 Rígidas
 Translação
 Rebatimento
 Rotação
 Mudança de Escala
 Não rígidas (Warping)

213. Rotação
 Rotação em torno de (ic, jc)
i'  (i  ic ) cos   ( j  jc ) sen   ic
j '  (i  ic ) sen   ( j  jc ) cos   jc

214. Rotação e Rebatimento
Imagem original Rebatimento pela Rotação de 90
diagonal graus em torno
de (R/2,C/2)

215. Ampliação (Zoom in)
 Por replicação de pixels
Original Ampliação por fator 3
10 10 10 10 10 10 10 10
20 30 10 10 10 10 10 10
10 10 10 10 10 10
20 20 20 30 30 30
20 20 20 30 30 30
20 20 20 30 30 30

216. Ampliação (Zoom in)
 Por interpolação bilinear
Original Ampliação por fator 3
10 10 10 10 10 10 10 10
20 30
Interpolação nas linhas
Passos de níveis de cinza:
20 23 27 30 33 37
10 a 10: 0
20 a 30: (30-20)/3 = 3,3

217. Ampliação (Zoom in)
 Por interpolação bilinear
Original Ampliação por fator 3
10 10 10 10 10 10 10 10
20 30 13 14 16 17 18 19
Interpolação nas colunas 17 19 21 23 25 28
Passos de níveis de cinza:
20 23 27 30 33 37
10 a 20: (20-10)/3 = 3,3
10 a 23: (23-10)/3 = 4,3 23 27 33 37 41 46
10 a 27: (27-10)/3 = 5,7 27 32 38 43 48 55
...

218. Ampliação (Zoom in)
 Exemplo: Ampliação por fator 10
Original Replicação Interpolação

219. Redução (Zoom out)
 Por eliminação de pixel
 Por Média
Original Redução por fator 3
10 10 10 10 10 10
14 18
13 14 16 17 18 19
28 41
17 19 21 23 25 28
20 23 27 30 33 37
23 27 33 37 41 46
27 32 38 43 48 55

220. Reconstrução de Imagens
 Zoom por fatores não inteiros
 Ex: F = 3,75432
 Operações elásticas, etc.
 Técnicas mais avançadas devem ser
utilizadas
 Uma dessas técnicas é a reconstrução
de imagens

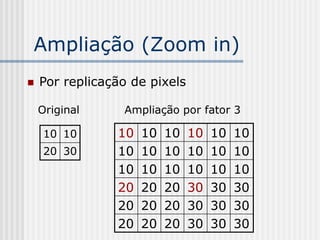
221. Reconstrução de imagens
 Dados f(i,j), f(i,j+1), f(i+1,j), f(i+1,j+1)
(i, j) (i, y) (i, j+1)
 Reconstrução:
Encontrar f(x,y), (x,y)
x em [i, i+1]
y em [j, j+1]
(i+1, j) (i+1, y) (i+1, j+1)

222. Reconstrução de imagens
por interpolação bilinear
 f(i, y) = f(i, j)+(y–j)[f(i, j+1)-f(i, j)]
 f(i+1,y)=f(i+1,j)+(y–j)[f(i+1,j+1)-f(i+1, j)]
 f(x, y) = f(i, y) + (x – i) [f(i+1, y) - f(i, y)]
(i, j) (i, y) (i, j+1)
(x,y)
(i+1, j) (i+1, y) (i+1, j+1)

223. Reconstrução de imagens
 Ex: f(10.5, 15.2)=?
 f(10, 15) = 10; f(10, 16) = 20;
f(11,15) = 30; f(11, 16) = 30

224. Reconstrução de imagens
Solução:
x = 10.5; y = 15.2 => i = 10; j = 15
f(i, y) = f(i, j)+(y–j)[f(i, j+1)-f(i, j)]
f(10, 15.2)=f(10,15)+(15.2-15)*[f(10,16)-f(10,15)
= 10 + 0.2*[20 – 10] = 12
f(i+1,y)=f(i+1,j)+(y–j)[f(i+1,j+1)-f(i+1, j)]
f(11, 15.2)=f(11,15)+(15.2-15)*[f(11,16)-f(11,15)
=30 + 0.2*[30 – 30] = 30
f(x, y) = f(i, y) + (x–i) [f(i+1, y) - f(i, y)]
f(10.5, 15.2)=12+(10.5-10)*[30-12] =21

225. Zoom por reconstrução de
imagens
Ex: Ampliação por fator 2.3
Passo para as coordenadas: 1/2.3 = 0.43
x = 0, 0.43, 0. 87, 1.30, 1.74, 2.17, 2.61, 3.04...
y = 0, 0.43, 0. 87, 1.30, 1.74, 2.17, 2.61, 3.04...
g(0,0) = f(0,0); g(0,1) = f(0, 0.43);
g(0,2) = f(0, 0.87); g(0,3) = f(0, 1.30);...
Ex: Redução por fator 2.3
x = 0, 2.3, 4.6, 6.9, 9.2, 11.5, 13.8...
y = 0, 2.3, 4.6, 6.9, 9.2, 11.5, 13.8...
g(0,0) = f(0,0); g(0,1) = f(0, 2.3);
g(0,2) = f(0, 4.6); g(0,3) = f(0,6.9);...

226. Operações Topológicas Não
Rígidas (warping)
 Warping = distorção
 Zoom por fator F(i, j)
 Rotação por ângulo teta(i,j)
 Translação com deslocamento d(i,j)
 Warping especificado pelo usuário

227. Warping baseado em
Campos
 Entretenimento
 Efeitos especiais, morphing
 Correção de distorções óticas
 Alinhamento de elementos
correspondentes em duas ou mais
imagens (registro)
 Modelagem e visualização de
deformações físicas

228. Warping baseado em
Campos
1. Características importantes da
imagem são marcados por
segmentos de reta orientados
(vetores de referência)
2. Para cada vetor de referência, um
vetor alvo é especificado, indicando
a transformação que se pretende
realizar

229. Warping baseado em
Campos
3. Para cada par de vetores
referência-alvo, encontra-se o
ponto X’ para onde um ponto X da
imagem deve migrar, de forma que
as relações espaciais entre X’ e o
vetor alvo sejam idênticas àquelas
entre X e o vetor de referência
4. Parâmetros para as relações
espaciais : u e v

230. Warping baseado em
Campos

231. Warping baseado em
Campos
 u: representa o
deslocamento
normalizado de P
até O no sentido
do vetor PQ
(Normalizado:
dividido pelo
módulo de PQ)
 |v|: distância de X
à reta suporte de
PQ

232. Warping baseado em
Campos
 Se O=P, u = 0
 Se O=Q, u = 1
 Se O entre P e
Q, 0<u<1;
 Se O após Q,
u>1
 Se O antes de
P, u<0

233. Warping baseado em
Campos
 Encontrar u e v: norma, produto interno,
vetores perpendiculares, projeção de um
vetor sobre outro.
 Vetores a = (x1, y1) e b = (x2, y2)
 Norma de a:
|| a ||  x  y
2
1
2
1
 Produto interno:
a.b = x1x2 +y1y2

234. Warping baseado em
Campos
 “Norma” da projeção de a sobre b (o
sinal indica o sentido em relação a b)
a
a.b
|| c || 
|| b ||
b
c

235. Warping baseado em
Campos
 Vetor b = (x2, y2) perpendicular a a =
(x1, y1) e de norma igual à de a:
b a
 Perpendicularidade: x1x2 +y1y2 = 0
 Mesma norma: x22 + y22 = x12 + y12

236. Warping baseado em
Campos
 Soluções:
x2 = y1, y2 = -x1
x2 = -y1, y2 = x1
b a
b’

237. Warping baseado em
Campos
 Parâmetro u:
“norma” da
projeção de PX
sobre PQ, dividido
pela norma de PQ
PX .PQ
u 2
|| PQ ||

238. Warping baseado em
Campos
 P = (xp,yp), Q =
(xq, yq), X = (x,y)
PX .PQ
u 2
|| PQ ||
u = (x - xp).(xq - xp) + (y -yp)(yq – yp)
(xq-xp)2 + (yq-yp)2

239. Warping baseado em
Campos
 Parâmetro v:
distância de X à
reta suporte de PQ
PX .  PQ
v
|| PQ ||
 v: vetor
perpendicular a v e
de mesma norma
que este.

240. Warping baseado em
Campos
 PQ = (Xq-Xp, Yq-Yp)
PQ1 = (Yq–Yp, Xp-Xq)
PQ2 = (Yp–Yq, Xq-Xp)
 Vamos usar PQ1

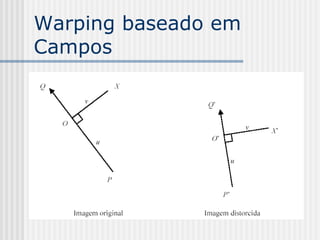
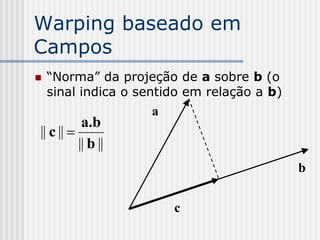
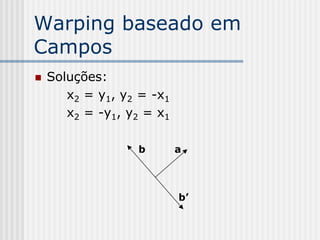
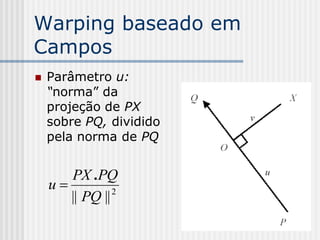
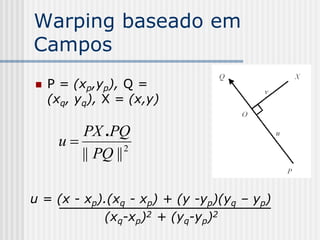
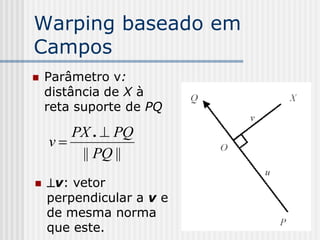
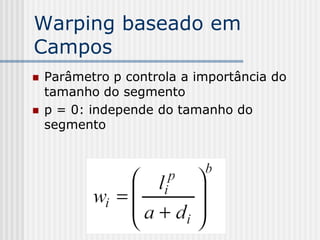
241. Warping baseado em
Campos
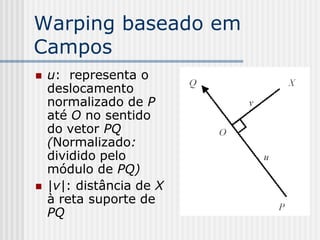
 Parâmetro v:
PX .  PQ
v
|| PQ ||
v = (x-xp)(yq-yp) + (y-yp)(xp–xq)
[(xq-xp)2 + (yq-yp)2]1/2

242. Warping baseado em
Campos
 Cálculo de X’:
v.  P ' Q'
X '  P'u.P' Q'
|| P' Q' ||

243. Warping baseado em
Campos
PX .PQ
u 2
|| PQ ||
PX .  PQ
v
|| PQ ||
v.  P ' Q'
X '  P'u.P' Q'
|| P' Q' ||

244. Warping baseado em
Campos
 Quando há mais de um par de vetores
referência-alvo, cada pixel sofre a
influência de todos os pares de vetores
 Será encontrado um ponto Xi’ diferente
para cada par de vetores referência-alvo.
 Os diferentes pontos para os quais o
ponto X da imagem original seria levado
por cada par de vetores referência-alvo
são combinados por intermédio de uma
média ponderada, produzindo o ponto X’
para onde X será efetivamente levado.

245. Warping baseado em
Campos

246. Warping baseado em
Campos
 Peso da coordenada definida pelo i-ésimo
par de vetores de referência-alvo:
di: Distância entre X e o segmento PiQi
li: ||Pi Qi||
a, b e p : Parâmetros não negativos

247. Warping baseado em
Campos
 Relação inversa com a distância entre a
reta e o ponto X
 Parâmetro a : Aderência ao segmento
 a = 0 (Peso infinito ou aderência máxima)

248. Warping baseado em
Campos
 Parâmetro p controla a importância do
tamanho do segmento
 p = 0: independe do tamanho do
segmento

249. Warping baseado em
Campos
 Parâmetro b controla a forma como a
influência decresce em função da
distância
 b = 0: peso independe da distância

250. Warping baseado em
Campos
 Bons resultados são obtidos com:
a entre 0 e 1
b=2
p = 0 ou p = 1.

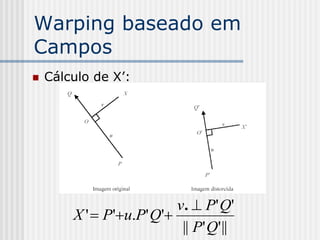
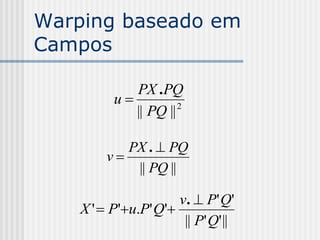
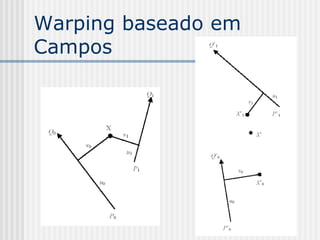
251. Warping baseado em
Campos
 Exemplo:
P0 = (40, 10); Q0 = (20, 5)
P0’ = (35, 15); Q0’ = (25, 20) 0 5 10 15 20 25 30 35 40 45 50 55 60
P1 = (20, 30); Q1 = (10, 35) 0
Q1‟
P1’ = (25, 50); Q1’ = (5, 40) 5
Q1
X = (20, 25) 10
u0 = [(20-40) (20-40) + (25- 15
10)(5-10)] / [(20-40)2+ X
(5-10)2] = 0.76
20 Q0
P1
v0 = [(20-40) (5-10) + (25- 25 Q0‟
P1‟
10)(40-20)] / [(20-40)2+ 30
(5-10)2]1/2 = 19.40
35
X0’ = (35, 10) + 0.76 (25-35, P0‟
20-15) + 19.4 (20-15, 35- 40
P0
X0‟
25) / [(25-35)2 + (20- 45
15)2]1/2
X0’ = (36.03, 31.17) 50

252. Warping baseado em
Campos
 Exemplo (cont):
u1 = [(20-20) (10-20) +
(25-30)(35-30)] / [(10-
20)2+ (35-30)2] = - 0.2 0 5 10 15 20 25 30 35 40 45 50 55 60
v1 = [(20-20) (35-30) + 0
(25-30)(20-10)] / [(10- 5 Q1‟
20)2+ (35-30)2]1/2 = - 10
Q1
4,47
15
X1’ = (25, 50) - 0.2 (5-25, X
40-50) -4,47 (40-50, 20 Q0
25-5) / [(25-5)2 + (40- 25 Q0‟
P1
50)2]1/2 P1‟
X1’ = (25, 50) + (4.6, 2) + 30
(2, -3.99) = (31.6, 35 X1‟
48,01) 40
P0‟ X0‟
P0
45
50

253. Warping baseado em
Campos
 Exemplo (cont):
Dados a = 0.1; b = 2; p= 0
wi = 1/[0.1+di]2
d0 = v0 = 19.4 => w0 =
0 5 10 15 20 25 30 35 40 45 50 55 60
0.0026
0
5 Q1‟
d1 = distância de X a P1 = Q1
[(20-20)2 + (25-30)2]1/2 10
= 5 =>: w1 = 0.0384 15
X’ = [0.0026* (36.03, 20 Q0
X
31.17) + 0.0384*(31.6, P1
48,01)]/( 0.0026+ 25 Q0‟
P1‟
0.0384) 30 X‟
X’ = (31.88, 46,94) X1‟
35
P0‟ X0‟
40
P0
45
50

254. Morphing
 Interpolação de formas e cores
entre duas imagens distintas
(f0 e fN-1)
 Encontrar imagens f1, f2, ..., fN-2:
transição gradual de f0 a fN-1
 Efeitos especiais na publicidade e na
indústria cinematográfica; realidade
virtual; compressão de vídeo; etc.

255. Morphing

256. Morphing
Warping de f0
cki
f0 fN-1
ai bi
“+”
Warping de fN-1
cki

257. Morphing
ai
c1i
c2i
c3i
c4i
c5i
c6i
c7i
c8i
c9i
bi

258. Morphing

259. Técnicas no Domínio da
Freqüência
 Conversão ao domínio da freqüência:
transformadas
 Processamento e análise no domínio da
freqüência
 Fourier, Cosseno Discreta, Wavelets,
etc.

260. Cosseno Analógico
 f: freqüência x(t )  A cos2ft   
 T=1/f: período A
  : fase
 A: amplitude
 Gráfico para
fase nula e A>0
T

261. Uma Família de Funções
Cosseno Analógicas
xk (t )  Ak cos2f k t   k , k  0, 1, ..., N  1
 fk: freqüência do k-ésimo cosseno
 Tk =1/fk: período do k-ésimo
cosseno
  k : fase do k-ésimo cosseno
 Ak: amplitude do k-ésimo cosseno

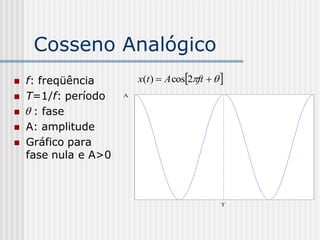
262. Uma Família de Funções
Cosseno Discretas
x k [n]  Ak cos2f k n   k , n  0,1,...,N  1
k = 0,1,...N-1

263. Uma Família de Funções
Cosseno Discretas
1/ 2
2
Ak    ck X k
N
1/2 1/2
 para k  0
ck 
1
 para k  1, 2, ... N - 1
k 2N k
fk  Tk  k 
2N k 2N
1/ 2
2  (2n  1)k 
x k [n ]    c k X k cos  , n  0,1,...,N  1
N  2N 

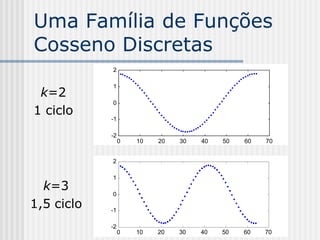
264. Uma Família de Funções
Cosseno Discretas
1/ 2
2  (2n  1)k 
x k [n ]    c k X k cos  , n  0,1,...,N  1
N  2N 
 f0  0 1/ 2
 2  1
1/ 2
k 0  x0[n]      X 0 , n  0,1,...,N  1
 0  0  N  2
1
k  1  f1   T1  2 N (meio-período em N amostras)
2N
N 1 2N
k  N  1  f N 1   TN 1 
2N N 1

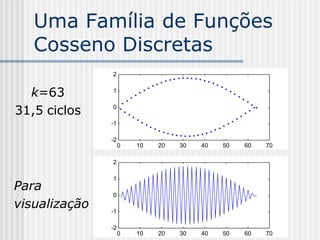
265. Uma Família de Funções
Cosseno Discretas
 xk[n] (N = 64, Xk = 10).
2
1
0
-1
-2
0 10 20 30 40 50 60 70
k=1
Meio-ciclo

266. Uma Família de Funções
Cosseno Discretas
2
1
k=2
0
1 ciclo
-1
-2
0 10 20 30 40 50 60 70
2
1
k=3 0
1,5 ciclo -1
-2
0 10 20 30 40 50 60 70

267. Uma Família de Funções
Cosseno Discretas
2
k=32 1
16 ciclos
0
-1
-2
0 10 20 30 40 50 60 70
2
1
Para 0
visualização -1
-2
0 10 20 30 40 50 60 70

268. Uma Família de Funções
Cosseno Discretas
2
k=63 1
31,5 ciclos 0
-1
-2
0 10 20 30 40 50 60 70
2
1
Para
0
visualização -1
-2
0 10 20 30 40 50 60 70

269. Uma Família de Funções
Cosseno Discretas
 Amostragem de um sinal periódico não
necessariamente produz um sinal de
mesmo período (ou mesmo periódico).

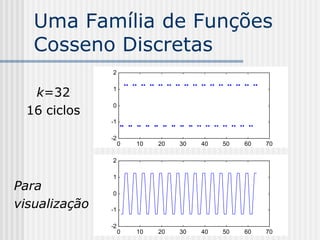
270. Somando Cossenos
Discretos
 Criar um sinal x[n] somando-se os sinais
xk[n], k = 0...N-1, amostra a amostra:
N 1
x[n]   x k [n], n 0,1,...,N  1
k 0
1 / 2 N 1
2  (2n  1)k 
x[n ]     ck X k cos  2 N , n  0,1,...,N  1
N k 0  

271. Somando Cossenos
Discretos
 Exemplo:
 N = 8; X0 = 10; X1 = 5; X2 = 8,5; X3 = 2;
X4 = 1; X5 = 1,5; X6 = 0; X7 = 0,1.
5
1/ 2
11
4 x 0 [n ]    10
22
3 =3.5355
2
0 2 4 6 8

272. Somando Cossenos
Discretos
 X1 = 5
4 5  (2n  1) 
x1 [n ]  cos 
2
2  16  
0
=2.4520; 2.0787; 1.3889;
-2
0.4877; -0.4877; -1.3889;
-4
0 2 4 6 8
-2.0787; -2.4520
6
4
x0[n]+x1[n]
2
0
0 2 4 6 8

273. Somando Cossenos
Discretos
 X2 = 8,5
8.5  (2n  1)2 
x 2 [n ] 
4
cos  
2
2  16 
0
= 3.9265; 1.6264; -1.6264;
-2
-3.9265; -3.9265; -1.626;
-4
0 2 4 6 8
1.6264; 3.9265
10
5
x0[n]+x1[n] +x2[n]
0
-5
0 2 4 6 8

274. Somando Cossenos
Discretos
 X3 = 2
1 2  (2n  1)3 
x 3 [n ]  cos  
0.5 2  16 
0
= 0.8315; -0.1951; -0.9808;
-0.5
-0.5556; 0.5556; 0.9808;
-1
0 2 4 6 8
0.1951; -0.8315
15
10
5 x0[n]+x1[n]+x2[n]+x3[n]
0
-5
0 2 4 6 8

275. Somando Cossenos
Discretos
 X4 = 1
0.4
1  (2n  1)4 
x 4 [n ]  cos  
 
0.2
2 16
0
= 0.3536; -0.3536; -0.3536;
-0.2
0.3536; 0.3536; -0.3536;
-0.4
0 2 4 6 8
-0.3536; 0.3536
15
10
5 x0[n]+x1[n]+x2[n]+x3[n]
0 +x4[n]
-5
0 2 4 6 8

276. Somando Cossenos
Discretos
 X5 = 1,5
1
1.5  (2n  1)5 
x 5 [n ]  cos  
 
0.5
2 16
0
-0.5
= 0.4167 -0.7356 0.1463
0.6236 -0.6236 -0.1463
-1
0 2 4 6 8 0.7356 -0.4167
15
10
5 x0[n]+x1[n]+x2[n]+x3[n]
0 +x4[n]+x5[n]
-5
0 2 4 6 8

277. Somando Cossenos
Discretos
 X6 = 0
0  (2n  1)6 
x 6 [n ]  cos 
1
0.5 2  16 

=0
0
-0.5
-1
0 2 4 6 8
15
10
5 x0[n]+x1[n]+x2[n]+x3[n]
0 +x4[n]+x5[n]+x6[n]
-5
0 2 4 6 8

278. Somando Cossenos
Discretos
 X7 = 0,1
0.1  (2n  1)7 
x 7 [n ] 
0.05
cos  
2  16 
0
= 0.0098; -0.0278; 0.0416;
-0.0490’; 0.0490; -0.0416;
-0.05
0 2 4 6 8
0.0278; -0.0098
15
10
5 x[n]=x0[n]+x1[n]+x2[n]+
0 x3[n] +x4[n]+x5[n]+x6[n]
-5
+x7[n]
0 2 4 6 8

279. Somando Cossenos
Discretos
 X[k] é um sinal digital: X[k]= X0, X1,...XN-1
 Exemplo: X[k]=10;5;8.5;2;1;1.5;0;0.1
 Dado X[k] pode-se obter x[n]
 X[k]: representação alternativa para x[n]
X[k] x[n]
10 15
10
5 5
0
0 -5
0 2 4 6 8 0 2 4 6 8

280. Somando Cossenos
Discretos
 xk[n]: cosseno componente de x[n],
de freqüência fk = k/2N; ou
 xk[n]: componente de freqüência
fk = k/2N;
 X[k]: Diretamente relacionado com a
amplitude da componente de
freqüência fk = k/2N
 X[k] representa a importância da
componente de freqüência fk = k/2N

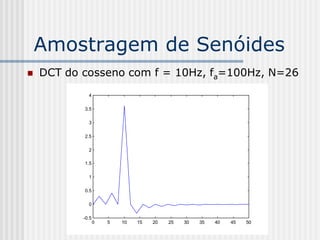
281. Transformada Cosseno
Discreta (DCT)
 DCT de x[n]:
1/ 2 N 1
2  (2n  1)k 
X [k ]    ck  x[n] cos  , k  0,1,...,N  1
N n 0  2N 
 Transformada DCT inversa (IDCT) de
X[k]:
1 / 2 N 1
2  (2n  1)k 
x[n]     ck X [k ] cos  2 N , n  0,1,...,N  1
N k 0  

282. Transformada Cosseno
Discreta (DCT)
 X[k]: coeficientes DCT
 X: representação de x no domínio da
freqüência
 X[0]: coeficiente DC (Direct Current)
 X[1]...X[N-1]: coeficientes AC
(Alternate Current)
 Complexidade
 Algoritmos eficientes: FDCT

283. DCT – Exemplo 1
g1
0.1
0
-0.1
-0.2
0 20 40 60 80 100 120
g3 g1+ g3
2 2
1 1
0 0
-1 -1
-2
-2
0 20 40 60 80 100 120 0 20 40 60 80 100 120

284. DCT – Exemplo 1 (Cont.)
g10 g1+g3+g10
2 2
1 1
0 0
-1 -1
-2
-2
0 20 40 60 80 100 120
0 20 40 60 80 100 120
g118 g1+g3+g10+g118
+
2
0.1
1
0 0
-0.1 -1
-2
-0.2
0 20 40 60 80 100 120 0 20 40 60 80 100 120

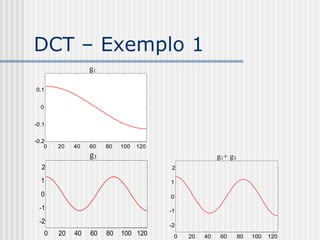
285. DCT – Exemplo 2
60  1 π 
f1[n]  29.99 cos 2 π n 
40  2N 2N 
20
0
-20
-40
-60
0 10 20 30 40 50 60
60  2 π  150 f1  f 2
f 2 [n]  48.54 cos 2 π n 
40  2N 2N 
100
20
50
0
-20 0
-40 -50
-60
-
0 10 20 30 40 50 60 0 10 20 30 40 50 60

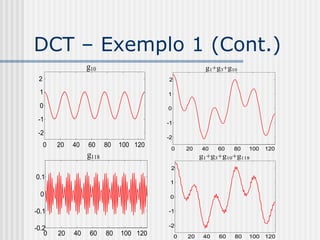
286. DCT – Exemplo 2 (Cont.)
60  3 π  150 f1  f 2  f 3
f 3 [n]  34.23 cos 2 π n 
40  2N 2N 
100
20
50
0
-20 0
-40 -50
-60
-
0 10 20 30 40 50 60 1000 10 20 30 40 50 60
60  4 π  150 f1  f 2  ...  f 4
f 4 [n]  -35.19 cos 2π n 
40  2N 2N 
100
20
50
0
-20 0
-40 -50
-60
-
0 10 20 30 40 50 60 0 10 20 30 40 50 60

287. DCT – Exemplo 2 (Cont.)
150
60  5 π  f 1  f 2  ...  f 6
f 5 [n]  -34.55 cos 2π n 
40  2N 2N  100
20 50
0 0
-20
-50
-40
-
-60 100
0 10 20 30 40 50 60 0 10 20 30 40 50 60
150
60  6 π  f 1  f 2  ...  f 6
f 6 [n]  -33.29 cos 2 π n 
40  2N 2N  100
20 50
0
0
-20
-50
-40
-60 -
100
0 10 20 30 40 50 60 0 10 20 30 40 50 60

288. DCT – Exemplo 2 (Cont.)
200
60  7 π  f 1  f 2  ...  f 7
f 7 [n]  -63.42 cos 2π n  150
40  2N 2N 
100
20
50
0
0
-20
-40 -50
-60 -
1000 10 20 30 40 50 60
0 10 20 30 40 50 60
60  8 π  f1  f 2  ...  f 8
f 8 [n]  -42.82 cos 2π n  200
40  2N 2N 
150
20
100
0
50
-20
0
-40
-50
-60
-
0 10 20 30 40 50 60 100

289. DCT – Exemplo 2 (Cont.)
60  9 π  f1  f 2  ...  f 9
f 9 [n]  -10.31cos 2 π n  200
40  2N 2N 
150
20 100
0 50
-20 0
-40 -50
-60 -
0 10 20 30 40 50 60 1000 10 20 30 40 50 60
60  10 π  f1  f 2  ...  f10
f10 [n]  7.18 cos 2 π n  200
40  2N 2N 
150
20 100
0 50
-20 0
-40 -50
-60 -
0 10 20 30 40 50 60 1000 10 20 30 40 50 60

290. DCT – Exemplo 2 (Cont.)
600
60  20 π  f 1  f 2  ...  f 20
f 20 [n]  -62.24 cos 2π n 
40  2N 2N 
400
20
0 200
-20
0
-40
-60
-
0 10 20 30 40 50 60 2000 10 20 30 40 50 60
60  40 π  100 f1  f 2  ...  f 40
f 40 [n]  35.54 cos 2 π n 
40  2N 2N  0
800
20 600
0 400
-20 200
-40 0
-60 -
200
0 10 20 30 40 50 60 0 10 20 30 40 50 60

291. DCT – Exemplo 2 (Cont.)
60  60 π  120 f1  f 2  ...  f 60
f 60 [n]  -6.73 cos 2π n  0
40  2N 2N  100
0800
20
600
0
400
-20 200
-40 0
-60 -
0 10 20 30 40 50 60 2000 10 20 30 40 50 60
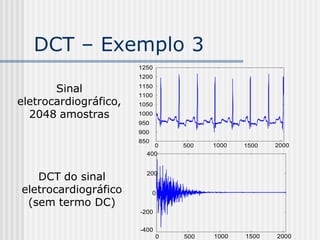
60  63 π  120 f1  f 2  ...  f 63
f 63 [n]  -1.51cos 2 π n 
 2N 2N  0
100
40
0800
20
600
0
400
-20
200
-40 0
-60 -
0 10 20 30 40 50 60 2000 10 20 30 40 50 60

292. DCT – Exemplo 3
1250
1200
Sinal 1150
1100
eletrocardiográfico, 1050
2048 amostras 1000
950
900
850
0 500 1000 1500 2000
400
DCT do sinal 200
eletrocardiográfico 0
(sem termo DC)
-200
-400
0 500 1000 1500 2000

293. DCT – Exemplo 4
20
Onda Quadrada 10
0
-10
-20
0 10 20 30 40 50 60
60
40
DCT da Onda 20
Quadrada 0
-20
-40
-60
0 10 20 30 40 50 60

294. Freqüências em Hz
 Ta = 1/fa (Período de amostragem)
 N amostras ---- (N-1)Ta segundos
1 1 fa
f1  (adimensio nal)  f1   Hz
2N 2( N  1)Ta 2( N  1)
fa fa
f N 1  ( N  1)  Hz
2( N  1) 2

295. Freqüências em Hz
 Aumentar N melhora a resolução de
freqüência.
 Aumentar fa aumenta a freqüência
máxima digitalizável, em Hz.
 Dualidade com o domínio do tempo

296. Freqüências em Hz
 Sinal de ECG, N= 2048, fa=360Hz
 Valores em Hz para k = 14, 70, 683 e 2047
14
70 683 2047

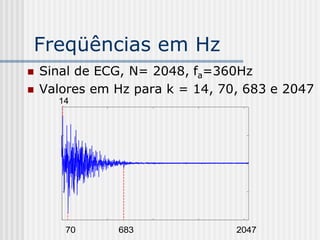
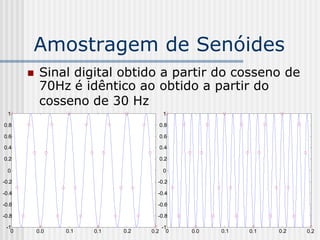
297. Freqüências em Hz
 f1 = fa/[2(N-1)] Hz = 360/(2x2047) =
0,087933561
 f14 = 14f1 = 1,23 Hz
 f70 = 70f1 = 6,16 Hz
 f683 = 683f1 = 60,06 Hz
 f2047 = 2047f1 = 180 Hz

298. Freqüências em Hz
 Observações
 fa = 360 Hz <=> Ta = 0,002778 Hz
 Tempo total para 2048 amostras = 5,69s
 Um batimento cardíaco: aprox. 0,8 s
 “Freqüência” Cardíaca: aprox. 1,25 bat./s
= 1,25 Hz, ou 75 batimentos/min.
 “Freqüência” Cardíaca aprox. igual a f14

299. Freqüências em Hz
 Onda quadrada, N = 64, fa = 1Hz
 Valores em Hz para k = 7, 8, 9 e 63
60
40
20
0
-20
-40
-60
0 7 9 63

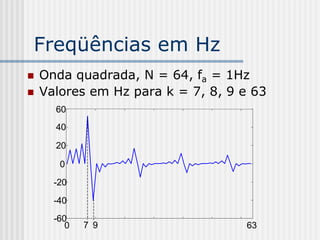
300. Freqüências em Hz
 f1 = fa/[2(N-1)] Hz = 1/(2x63) =
0,007936507
 f7 = 7f1 = 0,0556 Hz
 f8 = 8f1 = 0,0625 Hz
 f9 = 9f1 = 0,0714 Hz
 f63 = 63f1 = 0,5 Hz
 Obs:
 Período do sinal = 16 s
 Freqüência da onda = 0,0625

301. Freqüências e Conteúdo de
Freqüência
 Sinal periódico
 Freqüência
 Freqüências componentes
 Sinal não-periódico:
 Freqüências componentes

302. Sinais analógicos senoidais
 Representação em freqüência de um sinal
analógico senoidal?
 Sinal analógico senoidal, de freqüência f
 fa mínimo para digitalização adequada?
 Se f não é múltiplo de f1?

303. Amostragem de Senóides
 Cosseno com f=10Hz, fa=100Hz, N=26
1
0.8
0.6
0.4
0.2
0
-0.2
-0.4
-0.6
-0.8
-1
0 0.05 0.1 0.15 0.2 0.25

304. Amostragem de Senóides
 DCT do cosseno com f = 10Hz, fa=100Hz, N=26
4
3.5
3
2.5
2
1.5
1
0.5
0
-0.5
0 5 10 15 20 25 30 35 40 45 50

305. Amostragem de Senóides
 Vazamento de freqüência: mais de uma
componente de freqüência para uma
senóide
 Minimizar vazamento de freqüência:
aumentar N

306. Amostragem de Senóides
 Cosseno com f = 30Hz, fa=100Hz, N=26
1
0.8
0.6
0.4
0.2
0
-0.2
-0.4
-0.6
-0.8
-1
0 0.05 0.1 0.15 0.2 0.25

307. Amostragem de Senóides
 DCT do cosseno com f = 30Hz, fa=100Hz, N=26
3.5
3
2.5
2
1.5
1
0.5
0
-0.5
-1
-1.5
0 5 10 15 20 25 30 35 40 45 50

308. Amostragem de Senóides
 Cosseno com f = 48Hz, fa=100Hz, N=26
1
0.8
0.6
0.4
0.2
0
-0.2
-0.4
-0.6
-0.8
-1
0 0.05 0.1 0.15 0.2 0.25

309. Amostragem de Senóides
 DCT do cosseno com f = 48Hz, fa=100Hz, N=26
3.5
3
2.5
2
1.5
1
0.5
0
-0.5
0 5 10 15 20 25 30 35 40 45 50

310. Amostragem de Senóides
 Cosseno com f = 50Hz, fa=100Hz, N=26
1
0.8
0.6
0.4
0.2
0
-0.2
-0.4
-0.6
-0.8
-1
0 0.05 0.1 0.15 0.2 0.25

311. Amostragem de Senóides
 DCT do cosseno com f = 50Hz, fa=100Hz, N=26
5
4.5
4
3.5
3
2.5
2
1.5
1
0.5
0
0 5 10 15 20 25 30 35 40 45 50

312. Amostragem de Senóides
 Cosseno com f = 52Hz, fa=100Hz, N=26
1
0.8
0.6
0.4
0.2
0
-0.2
-0.4
-0.6
-0.8
-1
0 0.05 0.1 0.15 0.2 0.25

313. Amostragem de Senóides
 DCT do cosseno com f = 52Hz, fa=100Hz, N=26
3.5
3
2.5
2
1.5
1
0.5
0
-0.5
0 5 10 15 20 25 30 35 40 45 50

314. Amostragem de Senóides
 Sinal digital obtido a partir do cosseno de
52Hz é idêntico ao obtido a partir do
cosseno de 48 Hz
1 1
0.8 0.8
0.6 0.6
0.4 0.4
0.2 0.2
0 0
-0.2 -0.2
-0.4 -0.4
-0.6 -0.6
-0.8 -0.8
-1 -1
0 0.0 0.1 0.1 0.2 0.2 0 0.0 0.1 0.1 0.2 0.2

315. Amostragem de Senóides
 Cosseno com f = 70Hz, fa=100Hz, N=26
1
0.8
0.6
0.4
0.2
0
-0.2
-0.4
-0.6
-0.8
-1
0 0.05 0.1 0.15 0.2 0.25

316. Amostragem de Senóides
 DCT do cosseno com f = 70Hz, fa=100Hz, N=26
3.5
3
2.5
2
1.5
1
0.5
0
-0.5
-1
-1.5
0 5 10 15 20 25 30 35 40 45 50

317. Amostragem de Senóides
 Sinal digital obtido a partir do cosseno de
70Hz é idêntico ao obtido a partir do
cosseno de 30 Hz
1 1
0.8 0.8
0.6 0.6
0.4 0.4
0.2 0.2
0 0
-0.2 -0.2
-0.4 -0.4
-0.6 -0.6
-0.8 -0.8
-1 -1
0 0.0 0.1 0.1 0.2 0.2 0 0.0 0.1 0.1 0.2 0.2
5 5 5 5 5 5

318. Aliasing
 Na DCT, a maior freqüência é fa/2
 Aliasing: sinais senoidais de
freqüência f > fa/2 são discretizados
como sinais senoidais de freqüência
fd < fa / 2 (fd=fa–f, para fa/2 < f < fa)

319. Aliasing

320. Teorema de Shannon-
Nyquist
 Sinal analógico com fmax Hz
(componente)
 Digitalizar com fa Hz, tal que:
fa
 f max  f a  2 f max
2
 2fmax: Freq. de Nyquist

321. Digitalização de áudio
 Ouvido humano é sensível a freq.
entre 20Hz e 22KHz (aprox.)
 Digitalizar com 44KHz?
 Sons podem ter freqüências
componentes acima de 22KHz
 Digitalização a 44KHz: aliasing.
 Filtro passa-baixas com freqüência
de corte em 22KHz = Filtro anti-
aliasing

322. Eliminação de pixels
revisitada
 Por que redução de imagens por
eliminação de pixel deve ser evitada?
 Sinal original digitalizado com fa =2fmax
 No. de amostras do sinal digital
reduzido pela metade por eliminação de
amostras -> nova freqüência de
amostragem f’a = fa/2 = fmax ->
freqüência máxima do sinal analógico
digitalizada sem aliasing = f’a/2 = fmax/2

323. Eliminação de pixels
revisitada
 Por que redução de imagens (ou
outros sinais) por eliminação de
pixel (ou amostras) deve ser
evitada?
 Aliasing!
 Usar filtro passa-baixas!

324. Filtros no domínio da
freqüência
 Multiplicar o sinal no domínio da freq., S,
pela função de transferência do filtro, H
 Filtros:
 Passa-baixas
 Passa-altas
 Passa-faixa
 Corta-baixas
 Corta-altas
 Corta-faixa (faixa estreita: notch)

325. Filtros no domínio da freq.
 Ideais H Passa-baixas H Passa-altas
(corta-altas) (corta-baixas)
1 1
fc N-1 fc N-1
H Passa-faixa H corta-faixa
1 1
fc1 fc2 N-1 fc1 fc2 N-1

326. Filtros no domínio da
freqüência
 Combinação de filtros
 Filtros não-ideais (corte suave,
|H(fc)|=(1/2)1/2 ou |H(fc)|=1/2)

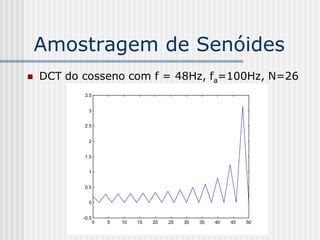
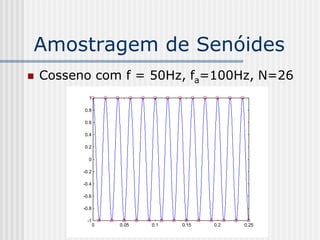
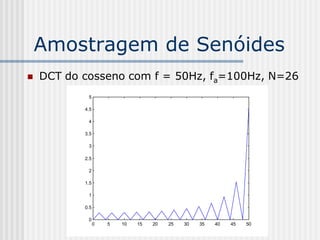
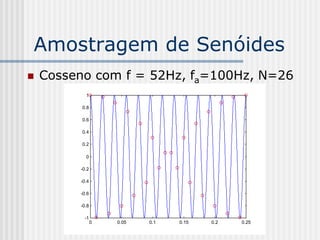
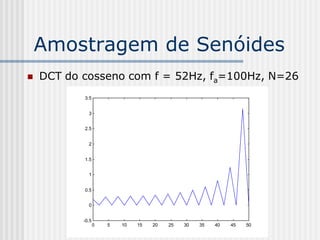
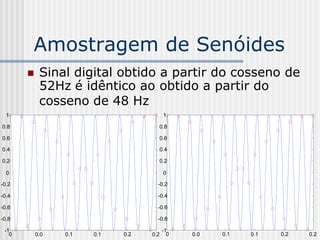
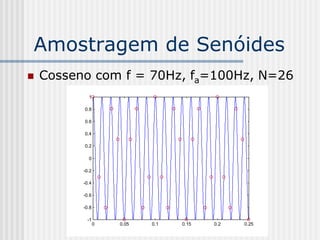
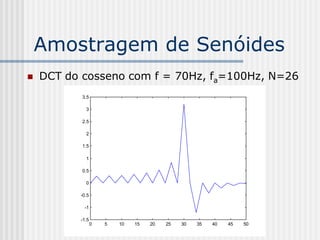
327. DCT 2-D
 Operação separável
 Complexidade elevada
N 1 N 1
1  (2m  1)k   (2n  1)l 
X [k , l ]  ck cl   x[m, n] cos   cos  2 N 
2N m 0 n 0  2N   
1 N 1N 1  (2k  1)m   (2l  1)n 
x[m, n]    ck cl X [k , l ] cos  2 N  cos  2 N 
2 N k 0 l 0    

328. DCT 2-D
 Imagem “cosseno na vertical”, 256 x 256,
8 ciclos (k = 16) e sua DCT normalizada

329. DCT 2-D
 Imagem “cosseno na vertical”, 256 x 256,
16 ciclos (k = 32) e sua DCT normalizada

330. DCT 2-D
 Imagem “cosseno na horizontal x cosseno
na vertical”, 256 x 256, 16 ciclos (k = 32)
e sua DCT normalizada

331. DCT 2-D
 Imagem “cosseno na horizontal x cosseno
na vertical”, 256 x 256, 8 x 16 ciclos e
sua DCT normalizada

332. DCT 2-D
 Imagem “Lena” (256x256) e sua DCT
normalizada

333. DCT 2-D
 Imagem “Lena” (256x256) e o log(DCT+1)
normalizado

334. Transformada de Fourier
Discreta (DFT)
N 1 j 2un
1 
 Direta: F [u ] 
N
 s[n]e N
n 0
N 1 j 2un
 Inversa: s[n ]   F [u]e N
u 0
n, u = 0, 1, ..., N-1
j  1
 Fórmula de Euler: e j  cos   j sen 

335. Duas propriedades
essenciais
F [u  N ]  ?
|F[-u]| = ?

336. Duas propriedades
essenciais
 DFT é periódica de período N:
F [u  N ]  F (u)
 Espectro de Fourier é função par:
|F[u]| = |F[-u]|

337. Esboço do Espectro de
Fourier
|F[u]|
u
-N/2 N/2 N-1
 u = 0, N, 2N,...: freq. 0
 u = N/2, 3N/2,...: freq. máxima (N par)
 u = (N-1)/2,...: freq. máxima (N ímpar)

338. Freqüências em Hz
 Ta = 1/fa (Período de amostragem)
 N amostras ---- (N-1)Ta segundos
1 1 fa
f1  (adimensio nal)  f1   Hz
N ( N  1)Ta N  1
N  1 fa fa
f( N 1) / 2   Hz
2 ( N  1) 2

339. Fourier 2-D
 Operação separável
 Complexidade elevada
C 1 R 1
1
F [u, v ] 
RC
  s[m, n]e  j 2 ( um / C  vn / R )
m 0n 0
C 1 R 1
s[m, n]    F [u, v]e j 2 ( um / C  vn / R )
u 0 v 0

340. Exibição do Espectro de
Fourier 2-D
Flog[u, v] = round[(L - 1) log(1+|F[u, v]|)/Fmax2]

341. Teorema da Convolução
 Se
g[m, n]  s[m, n]  h[m, n]
 Então:
 G[u,v] = H[u,v]F[u,v]
onde
G[u,v]: DFT de g[m,n]
F[u,v]: DFT de s[m,n]
H[u,v]: DFT de h[m,n]
 H[u,v]: Função de transferência do filtro

342. Filtros: espaço x freqüência
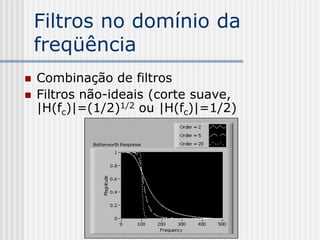
 Projeto de filtro no domínio da freqüência
(Fourier)
 Método imediato: H[k], k = 0..N-1
 Como filtrar sinais no domínio do tempo,
em tempo real?
 Convolução com h[n], n = 0..N-1 pode ser
proibitiva para n grande
 Encontrar ht[n], n = 0..M-1, com M < N,
de modo a obter uma aproximação
adequada para H[k].

343. Filtros: espaço x freqüência
 Para eficiência computacional e
redução de custos, o número de
coeficientes do filtro deve ser o
menor possível
 Projetar filtros relativamente imunes
ao truncamento

344. Questões do PosComp 2002
 51. Histograma de uma imagem com K tons de cinza é :
 a) Contagem dos pixels da imagem.
 b) Contagem do número de tons de cinza que ocorreram na imagem.
 c) Contagem do número de vezes que cada um dos K tons de cinza
ocorreu na imagem.
 d) Contagem do número de objetos encontrados na imagem.
 e) Nenhuma alternativa acima.
 52. filtro da mediana é :
 a) Indicado para detectar bordas em imagens.
 b) Indicado para atenuar ruído com preservação de bordas (i.é rápidas
transições de nível em
 imagens).
 c) Indicado para detectar formas específicas em imagens.
 d) Indicado para detectar tonalidades específicas em uma imagem.
 e) Nenhuma das respostas acima.

345. Questões do PosComp 2002
 51. Histograma de uma imagem com K tons de cinza é :
 a) Contagem dos pixels da imagem.
 b) Contagem do número de tons de cinza que ocorreram na imagem.
 c) Contagem do número de vezes que cada um dos K tons de
cinza ocorreu na imagem.
 d) Contagem do número de objetos encontrados na imagem.
 e) Nenhuma alternativa acima.
 52. filtro da mediana é :
 a) Indicado para detectar bordas em imagens.
 b) Indicado para atenuar ruído com preservação de bordas (i.é
rápidas transições de nível em
 imagens).
 c) Indicado para detectar formas específicas em imagens.
 d) Indicado para detectar tonalidades específicas em uma imagem.
 e) Nenhuma das respostas acima.

346. Questões do PosComp 2004
 56) Considerando as declarações abaixo, é incorreto afirmar:
 a) Filtros passa-altas são utilizados para detecção de bordas em imagens
 b) A transformada discreta de Fourier nos permite obter uma representação de
uma imagem no domínio freqüência
 c) Filtragem no domínio espacial é realizada por meio de uma operação chamada
“convolução”
 d) Os filtros Gaussiano e Laplaciano são exemplos de filtro passa-baixas
 e) O filtro da mediana pode ser utilizado para redução de ruído em uma imagem
 58) Identifique a declaração incorreta:
 a) As operações de ajuste de brilho e contraste são operações lineares
 b) A equalização de histograma é uma transformação não-linear e específica
para cada imagem
 c) A transformação necessária para calcular o negativo de uma imagem pode ser
aplicada simultaneamente (i.e., em paralelo) a todos pixels da imagem original
 d) A equalização de histograma pode ser obtida a partir de um histograma
cumulativo da imagem original
 e) O objetivo da equalização de histograma é reduzir o constrastre nas regiões
da imagem que correspondem à porção do histograma com maior concentração
de pixels

347. Questões do PosComp 2004
 56) Considerando as declarações abaixo, é incorreto afirmar:
 a) Filtros passa-altas são utilizados para detecção de bordas em imagens
 b) A transformada discreta de Fourier nos permite obter uma representação de
uma imagem no domínio freqüência
 c) Filtragem no domínio espacial é realizada por meio de uma operação chamada
“convolução”
 d) Os filtros Gaussiano e Laplaciano são exemplos de filtro passa-baixas
 e) O filtro da mediana pode ser utilizado para redução de ruído em uma imagem
 58) Identifique a declaração incorreta:
 a) As operações de ajuste de brilho e contraste são operações lineares
 b) A equalização de histograma é uma transformação não-linear e específica
para cada imagem
 c) A transformação necessária para calcular o negativo de uma imagem pode ser
aplicada simultaneamente (i.e., em paralelo) a todos pixels da imagem original
 d) A equalização de histograma pode ser obtida a partir de um histograma
cumulativo da imagem original
 e) O objetivo da equalização de histograma é reduzir o constrastre nas regiões
da imagem que correspondem à porção do histograma com maior concentração
de pixels

348. Questões do PosComp 2005
 59. O processo de análise de imagens é uma seqüência de etapas que são iniciadas a
partir da definição do problema. A seqüência correta destas etapas é:
 (a) pré-processamento, aquisição, segmentação, representação, reconhecimento.
 (b) aquisição, pré-processamento, segmentação, representação, reconhecimento.
 (c) aquisição, pré-processamento, representação, segmentação, reconhecimento.
 (d) aquisição, representação, pré-processamento, segmentação, reconhecimento.
 (e) pré-processamento, aquisição, representação, segmentação, reconhecimento.
 60. O termo imagem se refere a uma função bidimensional de intensidade de luz,
denotada por f(x; y), onde o valor ou amplitude de f nas coordenadas espaciais (x;
y) representa a intensidade (brilho) da imagem neste ponto. Para que uma imagem
possa ser processada num computador, a função f(x; y) deve ser discretizada tanto
espacialmente quanto em amplitude. Estes dois processos recebem as seguintes
denominações, respectivamente:
 (a) translação e escala.
 (b) resolução e escala.
 (c) resolução e ampliação.
 (d) amostragem e quantização.
 (e) resolução e quantização.

349. Questões do PosComp 2005
 59. O processo de análise de imagens é uma seqüência de etapas que são iniciadas a
partir da definição do problema. A seqüência correta destas etapas é:
 (a) pré-processamento, aquisição, segmentação, representação, reconhecimento.
 (b) aquisição, pré-processamento, segmentação, representação, reconhecimento.
 (c) aquisição, pré-processamento, representação, segmentação, reconhecimento.
 (d) aquisição, representação, pré-processamento, segmentação, reconhecimento.
 (e) pré-processamento, aquisição, representação, segmentação, reconhecimento.
 60. O termo imagem se refere a uma função bidimensional de intensidade de luz,
denotada por f(x; y), onde o valor ou amplitude de f nas coordenadas espaciais (x;
y) representa a intensidade (brilho) da imagem neste ponto. Para que uma imagem
possa ser processada num computador, a função f(x; y) deve ser discretizada tanto
espacialmente quanto em amplitude. Estes dois processos recebem as seguintes
denominações, respectivamente:
 (a) translação e escala.
 (b) resolução e escala.
 (c) resolução e ampliação.
 (d) amostragem e quantização.
 (e) resolução e quantização.

350. Questões do PosComp 2006
 47. [TE] Considere os filtros espaciais da média (m) e Mediana (M)
aplicados em imagens em níveis de cinza f e g. Qual par de termos ou
expressões a seguir não está associado, respectivamente, a características
gerais de m e M?
 (a) m(f + g) = m(f) + m(g); M(f + g) != M(f) + M(g)
 (b) ruído gaussiano; ruído impulsivo
 (c) convolução; filtro estatístico da ordem
 (d) preservação de pequenos componentes; não preservação de pequenos
componentes
 (e) filtragem com preservação de contornos; filtragem sem preservação de
contornos
 48. [TE] A convolução da máscara [-1 2 -1] com uma linha de uma
imagem contendo uma seqüência de pixels do tipo [... 3 4 5 6 7 8 9 10 ...]
resulta na transformação (sem considerar efeitos de borda):
 (a) [...3 4 5 6 7 8 9 10...] e representa o filtro da média com 2-vizinhos mais
próximos
 (b) [...0 0 0 0 0 0 0 0...] e representa o laplaciano no espaço discreto
 (c) [...0 0 0 0 0 0 0 0...] e representa uma erosão morfológica
 (d) [...1 1 1 1 1 1 1 1...] e é equivalente a um filtro passa-baixas
 (e) [...7 9 11 13 15 17 19...] e é equivalente a um filtro passa-altas

351. Questões do PosComp 2006
 47. [TE] Considere os filtros espaciais da média (m) e Mediana (M)
aplicados em imagens em níveis de cinza f e g. Qual par de termos ou
expressões a seguir não está associado, respectivamente, a características
gerais de m e M?
 (a) m(f + g) = m(f) + m(g); M(f + g) != M(f) + M(g)
 (b) ruído gaussiano; ruído impulsivo
 (c) convolução; filtro estatístico da ordem
 (d) preservação de pequenos componentes; não preservação de pequenos
componentes
 (e) filtragem com preservação de contornos; filtragem sem preservação de
contornos
 48. [TE] A convolução da máscara [-1 2 -1] com uma linha de uma
imagem contendo uma seqüência de pixels do tipo [... 3 4 5 6 7 8 9 10 ...]
resulta na transformação (sem considerar efeitos de borda):
 (a) [...3 4 5 6 7 8 9 10...] e representa o filtro da média com 2-vizinhos mais
próximos
 (b) [...0 0 0 0 0 0 0 0...] e representa o laplaciano no espaço discreto
 (c) [...0 0 0 0 0 0 0 0...] e representa uma erosão morfológica
 (d) [...1 1 1 1 1 1 1 1...] e é equivalente a um filtro passa-baixas
 (e) [...7 9 11 13 15 17 19...] e é equivalente a um filtro passa-altas

352. Questões do PosComp 2007
 61. [TE] O realce de imagem tem como objetivo destacar detalhes
finos procurando obter uma representação mais adequada do que
a imagem original para uma determinada aplicação. Dessa forma,
sobre as técnicas utilizadas no realce de imagens, é CORRETO
afirmar que
 (a) o melhor resultado obtido depende do filtro aplicado na imagem.
Normalmente, o mais aplicado é o filtro da mediana.
 (b) o melhor resultado é obtido com a aplicação de filtros passa-
baixas, cujos parâmetros dependem do resultado desejado.
 (c) a aplicação de filtros da média sempre oferece resultado adequado
no realce de imagens.
 (d) o resultado mais adequado no realce de imagens está associado à
aplicação de filtro passa-altas e da interpretação subjetiva do
observador que deverá ter conhecimento a priori da imagem original.
 (e) o resultado mais adequado no realce de imagens está associado à
aplicação de filtro passa-baixas e da interpretação subjetiva do
observador que deverá ter conhecimento a priori da imagem original.
 62 e 63

353. Questões do PosComp 2007
 61. [TE] O realce de imagem tem como objetivo destacar detalhes
finos procurando obter uma representação mais adequada do que
a imagem original para uma determinada aplicação. Dessa forma,
sobre as técnicas utilizadas no realce de imagens, é CORRETO
afirmar que
 (a) o melhor resultado obtido depende do filtro aplicado na imagem.
Normalmente, o mais aplicado é o filtro da mediana.
 (b) o melhor resultado é obtido com a aplicação de filtros passa-
baixas, cujos parâmetros dependem do resultado desejado.
 (c) a aplicação de filtros da média sempre oferece resultado adequado
no realce de imagens.
 (d) o resultado mais adequado no realce de imagens está associado à
aplicação de filtro passa-altas e da interpretação subjetiva do
observador que deverá ter conhecimento a priori da imagem original.
 (e) o resultado mais adequado no realce de imagens está associado à
aplicação de filtro passa-baixas e da interpretação subjetiva do
observador que deverá ter conhecimento a priori da imagem original.