Mod6 arvore falhas2008

Curso de Especialização em Transporte Ferroviário de Carga
MÓDULO 6MÓDULO 6
ÁRVORE DE FALHASÁRVORE DE FALHAS

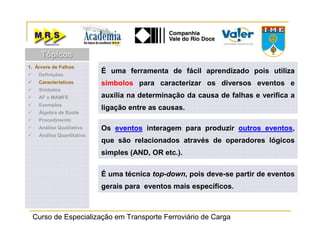
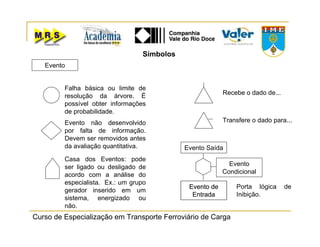
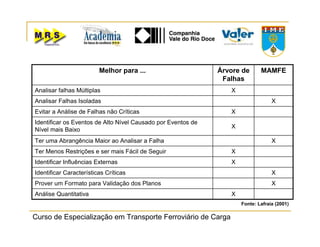
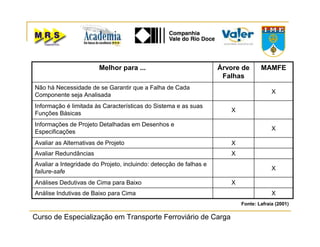
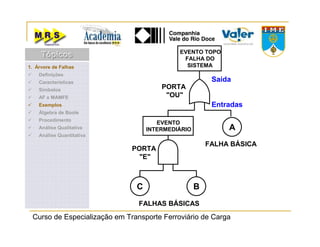
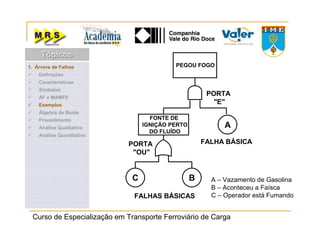
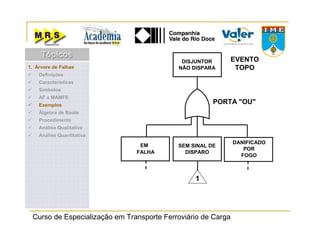
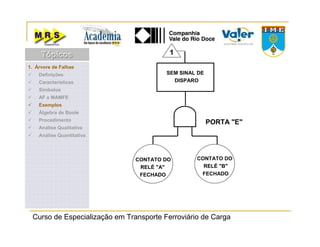
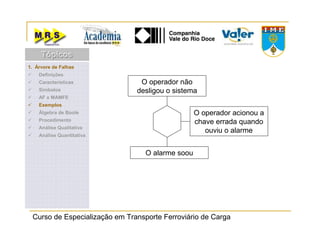
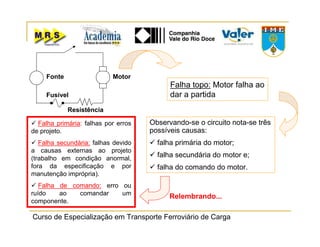
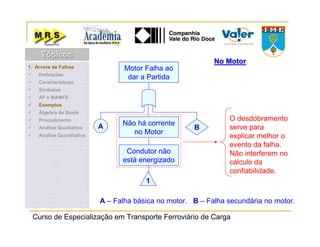
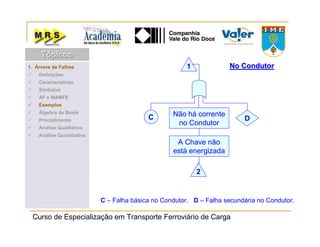
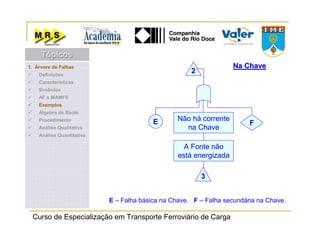
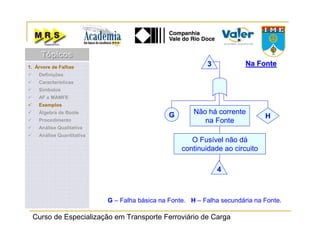
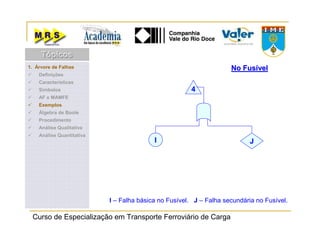
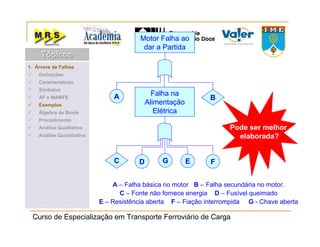
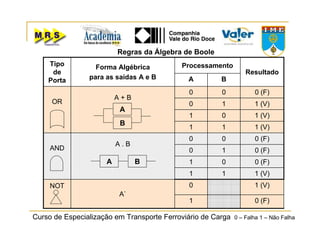
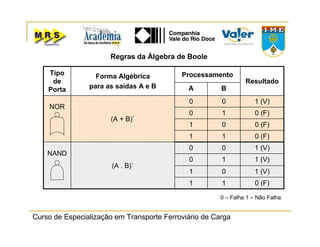
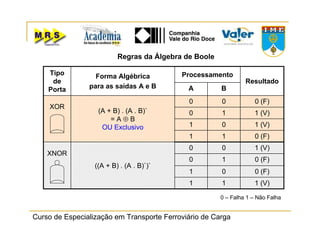
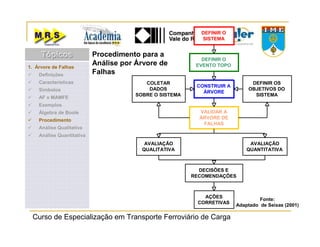
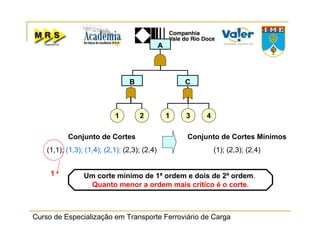
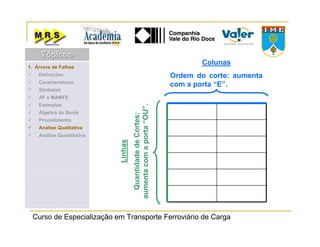
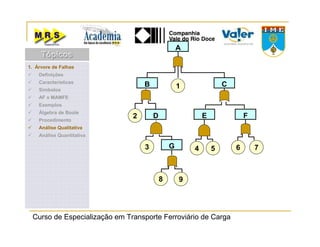
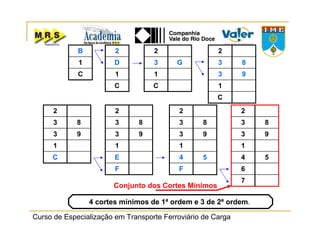
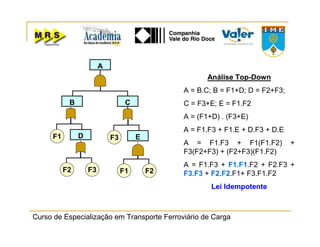
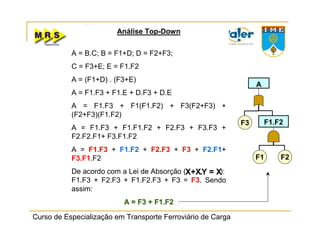
O Método de Análise da Árvore de Falhas (Failure Tree
Analysis - FTA) foi desenvolvido por volta de 1960, por
W.A.Watson, da Bell Laboratories e aperfeiçoada pela
Boeing Corporation.
1. Árvore de Falhas
Definições
Características
Símbolos
AF x MAMFE
Exemplos
Álgebra de Boole
Procedimento
Análise Qualitativa
Análise Quantitativa
TópicosTópicosTópicos
Consiste em um processo lógico e dedutivo que,
partindo de um evento indesejado e pré-definido
(EVENTO TOPO), busca-se as possíveis causas de tal
evento (pensamento reverso).

Visa melhorar a confiabilidade de produtos e de
processos por intermédio da análise sistemática de
possíveis falhas e suas conseqüências, orientando na
adoção de medidas corretivas ou preventivas.
A elaboração da Árvore de Falhas trás uma série de
OUTROS benefícios, tais como o aumento do domínio
das características técnicas dos equipamentos que
compõem o sistema, a identificação da seqüência das
falhas críticas e a melhor interação entre os integrantes
das equipes de projeto, operação e manutenção.
Definições
Características
Símbolos
AF x MAMFE
Exemplos
Álgebra de Boole
Procedimento

Pode ser desenvolvida em diferentes níveis de
complexidade.
É de interpretação simples por pessoas distantes do
assunto sob análise.
É aplicável tanto para a análise de um projeto quanto
para sistemas que já estão em operação.
Pode ser utilizada para avaliação qualitativa
(determinação das falhas básicas) e quantitativa
(cálculo da probabilidade de ocorrência do evento).
Definições
Características
Símbolos
AF x MAMFE
Exemplos
Álgebra de Boole
Procedimento

Os eventos interagem para produzir outros eventos,
que são relacionados através de operadores lógicos
simples (AND, OR etc.).
É uma ferramenta de fácil aprendizado pois utiliza
símbolos para caracterizar os diversos eventos e
auxilia na determinação da causa de falhas e verifica a
ligação entre as causas.
É uma técnica top-down, pois deve-se partir de eventos
gerais para eventos mais específicos.
Definições
Características
Símbolos
AF x MAMFE
Exemplos
Álgebra de Boole
Procedimento

Evento de
Entrada
Evento de
Entrada
Evento
Condicional
Evento Saída
Evento
Falha básica ou limite de
resolução da árvore. É
possível obter informações
de probabilidade.
Evento não desenvolvido
por falta de informação.
Devem ser removidos antes
da avaliação quantitativa.
Casa dos Eventos: pode
ser ligado ou desligado de
acordo com a análise do
especialista. Ex.: um grupo
gerador inserido em um
sistema, energizado ou
não.
Porta lógica de
Inibição.
Transfere o dado para...
Recebe o dado de...
Símbolos

Tanto o MAMFE quanto a Árvore de Falhas são
métodos para previsão de falhas em processos e
produtos;
Tanto o MAMFE quanto a Árvore de Falhas Podem
ser utilizados para analisar problemas existentes;
A Árvore de Falhas pode subsidiar o MAMFE;
Cada falha básica da Árvore de Falhas pode ser um
item do MAMFE, facilitando a avaliação dos efeitos e
da causa; da falha.
Definições
Características
Símbolos
AF x MAMFE
Exemplos
Álgebra de Boole
Procedimento

XAnálise Quantitativa
XProver um Formato para Validação dos Planos
XIdentificar Características Críticas
XIdentificar Influências Externas
XTer Menos Restrições e ser mais Fácil de Seguir
XTer uma Abrangência Maior ao Analisar a Falha
X
Identificar os Eventos de Alto Nível Causado por Eventos de
Nível mais Baixo
XEvitar a Análise de Falhas não Críticas
XAnalisar Falhas Isoladas
XAnalisar falhas Múltiplas
MAMFEÁrvore de
Falhas
Melhor para ...
Fonte: Lafraia (2001)

XAnálise Indutivas de Baixo para Cima
XAnálises Dedutivas de Cima para Baixo
X
Avaliar a Integridade do Projeto, incluindo: detecção de falhas e
failure-safe
XAvaliar Redundâncias
XAvaliar as Alternativas de Projeto
X
Informações de Projeto Detalhadas em Desenhos e
Especificações
X
Informação é limitada às Características do Sistema e as suas
Funções Básicas
X
Não há Necessidade de se Garantir que a Falha de Cada
Componente seja Analisada
MAMFEÁrvore de
Falhas
Melhor para ...
Fonte: Lafraia (2001)

EVENTO TOPO
FALHA DO
SISTEMA
EVENTO
INTERMEDIÁRIO A
BC
PORTA
"OU"
PORTA
"E"
FALHAS BÁSICAS
FALHA BÁSICA
Entradas
Saída
Definições
Características
Símbolos
AF x MAMFE
Exemplos
Álgebra de Boole
Procedimento

PEGOU FOGO
FONTE DE
IGNIÇÃO PERTO
DO FLUÍDO
A
BC
PORTA
"OU"
PORTA
"E"
FALHAS BÁSICAS
FALHA BÁSICA
A – Vazamento de Gasolina
B – Aconteceu a Faísca
C – Operador está Fumando
Definições
Características
Símbolos
AF x MAMFE
Exemplos
Álgebra de Boole
Procedimento

DISJUNTOR
NÃO DISPARA
DANIFICADO
POR
FOGO
SEM SINAL DE
DISPARO
EM
FALHA
EVENTO
TOPO
PORTA "OU"
1
Definições
Características
Símbolos
AF x MAMFE
Exemplos
Álgebra de Boole
Procedimento

SEM SINAL DE
DISPARO
CONTATO DO
RELÉ "B"
FECHADO
CONTATO DO
RELÉ "A"
FECHADO
PORTA "E"
1
Definições
Características
Símbolos
AF x MAMFE
Exemplos
Álgebra de Boole
Procedimento

O operador não
desligou o sistema
O alarme soou
O operador acionou a
chave errada quando
ouviu o alarme
Definições
Características
Símbolos
AF x MAMFE
Exemplos
Álgebra de Boole
Procedimento

Corte de Força
Desnecessário
B
A B C
O evento de saída ocorre se o
evento B ocorrer.
A – Monitor 1 gera o sinal errado.
B – Idem Monitor 2.
C – Idem Monitor 3.
Definições
Características
Símbolos
AF x MAMFE
Exemplos
Álgebra de Boole
Procedimento

Falha topo: Motor falha ao
dar a partida
Observando-se o circuito nota-se três
possíveis causas:
falha primária do motor;
falha secundária do motor e;
falha do comando do motor.
Falha primária: falhas por erros
de projeto.
Falha secundária: falhas devido
a causas externas ao projeto
(trabalho em condição anormal,
fora da especificação e por
manutenção imprópria).
Falha de comando: erro ou
ruído ao comandar um
componente.
Relembrando...
Fonte Motor
Fusível
Resistência

Considerando que diferentesConsiderando que diferentes
especialistas podem elaborarespecialistas podem elaborar
árvore de falhas diferentes, paraárvore de falhas diferentes, para
um mesmo sistema, podeum mesmo sistema, pode--sese
observar a solução a seguir.observar a solução a seguir.
A construção de uma Árvore deA construção de uma Árvore de
Falhas é um misto de arte e deFalhas é um misto de arte e de
ciência.ciência.
Professor Apostalikis apud Scapin (1999)

Primeira VersãoPrimeira Versão

A – Falha básica no motor. B – Falha secundária no motor.
No MotorNo Motor
Motor Falha ao
dar a Partida
Não há corrente
no Motor
Condutor não
está energizado
A B
O desdobramento
serve para
explicar melhor o
evento da falha.
Não interferem no
cálculo da
confiabilidade.
1
Definições
Características
Símbolos
AF x MAMFE
Exemplos
Álgebra de Boole
Procedimento

C – Falha básica no Condutor. D – Falha secundária no Condutor.
No CondutorNo Condutor
Não há corrente
no Condutor
A Chave não
está energizada
C D
2
Definições
Características
Símbolos
AF x MAMFE
Exemplos
Álgebra de Boole
Procedimento

E – Falha básica na Chave. F – Falha secundária na Chave.
Na ChaveNa Chave
Não há corrente
na Chave
A Fonte não
está energizada
E F
3
2
Definições
Características
Símbolos
AF x MAMFE
Exemplos
Álgebra de Boole
Procedimento

G – Falha básica na Fonte. H – Falha secundária na Fonte.
Na FonteNa Fonte
Não há corrente
na Fonte
O Fusível não dá
continuidade ao circuito
G H
4
Definições
Características
Símbolos
AF x MAMFE
Exemplos
Álgebra de Boole
Procedimento

I – Falha básica no Fusível. J – Falha secundária no Fusível.
No FusívelNo Fusível
I J
4
Definições
Características
Símbolos
AF x MAMFE
Exemplos
Álgebra de Boole
Procedimento

Segunda VersãoSegunda Versão

A – Falha básica no motor B – Falha secundária no motor.
C – Fonte não fornece energia D – Fusível queimado
E – Resistência aberta F – Fiação interrompida G - Chave aberta
Pode ser melhor
elaborada?
Motor Falha ao
dar a Partida
Falha na
Alimentação
Elétrica
A B
C D FEG
Definições
Características
Símbolos
AF x MAMFE
Exemplos
Álgebra de Boole
Procedimento

1 (V)11
0 (F)01
0 (F)10
0 (F)00
A . B
AND
1 (V)11
1 (V)01
1 (V)10
0 (F)00
A + B
OR
B
Resultado
ProcessamentoForma Algébrica
para as saídas A e B
Tipo
de
Porta
1 (V)0
A`
0 (F)1
A
NOT
Regras da Álgebra de Boole
A B
A
B
0 – Falha 1 – Não Falha

0 (F)11
0 (F)01
0 (F)10
1 (V)00
(A + B)`
NOR
1
0
1
0
B
Resultado
Tipo
de
Porta
1 (V)0
(A . B)`
1 (V)0
1 (V)1
A
0 (F)1
NAND

0 (F)11
1 (V)01
1 (V)10
0 (F)00
(A + B) . (A . B)`
= A ⊕ B
OU Exclusivo
XOR
1
0
1
0
B
Resultado
Tipo
de
Porta
1 (V)0
((A + B) . (A . B)`)`
0 (F)0
0 (F)1
A
1 (V)1
XNOR

Propriedades da Álgebra de Boole
1 - Lei Comutativa:
X.Y = Y.X
X+Y = Y+X
2 - Lei Associativa:
X(Y.Z) = (X.Y)Z
X+(Y+Z) = (X+Y)+Z
3 - Lei Idempotente:
X.X = X
X+X = X
4 - Lei de Absorção:
X(X+Y) = X
X+X.Y = X
Definições
Características
Símbolos
AF x MAMFE
Exemplos
Álgebra de Boole
Procedimento

Propriedades da Álgebra de Boole
5 - Lei Distributiva:
X(Y+Z) = X.Y+X.Z
(X+Y).(X+Z) = X+Y.Z
6 - Complementar:
X.X = 0
X+X = 1
7 - Teorema de "De Morgan":
X.Y = X+Y
X+Y = X.Y
8 - De uso freqüente:
X+X.Y = X+Y
X(X+Y) = X.Y
Definições
Características
Símbolos
AF x MAMFE
Exemplos
Álgebra de Boole
Procedimento

DEFINIR O
SISTEMA
DEFINIR O
EVENTO TOPO
CONSTRUIR A
ÁRVORE
DEFINIR OS
OBJETIVOS DO
SISTEMA
COLETAR
DADOS
SOBRE O SISTEMA
VALIDAR A
ÁRVORE DE
FALHAS
AVALIAÇÃO
QUANTITATIVA
AVALIAÇÃO
QUALITATIVA
DECISÕES E
RECOMENDAÇÕES
AÇÕES
CORRETIVAS
Procedimento para a
Análise por Árvore de
Falhas
Fonte:
Adaptado de Seixas (2001)
Definições
Características
Símbolos
AF x MAMFE
Exemplos
Álgebra de Boole
Procedimento

Definir o Sistema
Caracterizar o sistema e definir as suas funções;
Avaliar a operação do sistema (controles, interfaces
etc.);
Identificar os procedimentos operacionais do
sistema;
Identificar os procedimentos de teste e de
manutenção do sistema;
Analisar as especificações técnicas (limites
operacionais, necessidade de monitoração etc.) dos
componentes do sistema.
Definições
Características
Símbolos
AF x MAMFE
Exemplos
Álgebra de Boole
Procedimento

Definir o Evento Topo
Geralmente está relacionado com alguma situação
crítica;
Deve-se preocupar com a sua seleção:
Não pode ser muito geral, pois a análise pode se
tornar dispersa (pouco valor prático) e
Não pode ser muito específico, pois a análise
pode não fornecer uma visão suficientemente
ampla do problema.
Definições
Características
Símbolos
AF x MAMFE
Exemplos
Álgebra de Boole
Procedimento

Determinação da Probabilidade de Ocorrência.
Determinar o Evento Topo;
Determinar os Fatores Contribuintes;
Determinação das Falhas Básicas;
Simplificação Booleana;
Aplicação dos Dados Quantitativos;
Elaboração da Diagramação Lógica; ...
Construir a Árvore
Definições
Características
Símbolos
AF x MAMFE
Exemplos
Álgebra de Boole
Procedimento

O objetivo da validação da árvore de falhas é
avaliar a precisão e a veracidade das suas
informações.
Validar a Árvore de Falhas
Geralmente é efetuada por um analista que não
tenha participado da sua elaboração.
Definições
Características
Símbolos
AF x MAMFE
Exemplos
Álgebra de Boole
Procedimento

A determinação dos cortes mínimos viabiliza a análise
qualitativa da árvore de falhas
Denomina-se “corte” de uma arvore de falhas a um
conjunto de falhas básicas cuja a ocorrência implica na
ocorrência do evento topo.
Denomina-se “corte mínimo” quando o corte não puder
ser reduzido sem perder a sua condição de corte. Os
cortes mínimos são os pontos fracos do sistema sob
análise.
Definições
Características
Símbolos
AF x MAMFE
Exemplos
Álgebra de Boole
Procedimento

A
CB 1
1 2 1 3 4
Conjunto de Cortes
(1,1); (1,3); (1,4); (2,1); (2,3); (2,4)
1
Conjunto de Cortes Mínimos
(1); (2,3); (2,4)
Um corte mínimo de 1ª ordem e dois de 2ª ordem.
Quanto menor a ordem mais crítico é o corte.

Algoritmo para Determinar os Conjuntos de
Corte Mínimo
Algoritmo de Vesely-Fussel
Foi desenvolvido por Jerry Fussel e Willian Vesely e
pode ser utilizado para eventos não repetidos.
Parte-se da primeira porta antes do evento topo;
Para Portas tipo “E” aumenta-se o “tamanho” de um
corte mínimo e para Portas tipo “OU” aumenta-se a
“quantidade” de um corte mínimo;
Deve-se substituir cada porta pelas suas entradas
até que todas as portas tenham sido substituídas.
Definições
Características
Símbolos
AF x MAMFE
Exemplos
Álgebra de Boole
Procedimento

Colunas
Ordem do corte: aumenta
com a porta “E”.
Linhas
QuantidadedeCortes:
aumentacomaporta“OU”.
Definições
Características
Símbolos
AF x MAMFE
Exemplos
Álgebra de Boole
Procedimento

A
CB 1
FE
5 874
2 D
3 G
1
2
3 4 5 6 7
8 9
Definições
Características
Símbolos
AF x MAMFE
Exemplos
Álgebra de Boole
Procedimento

1
C
B 2
1
C
D G
2
1
C
3
1
9
8
2
3
C
3
1
9
8
2
3
C
3
F
1
9
8
2
3
E
3
F
1
5
9
8
2
3
4
3
7
6
1
5
9
8
2
3
4
3
Conjunto dos Cortes Mínimos
4 cortes mínimos de 1ª ordem e 3 de 2ª ordem.

Considerar-se-á na análise quantitativa, as taxas de
falha e de reparo como constantes.
A análise quantitativa pode ser efetuada
independentemente da análise qualitativa.
Definições
Características
Símbolos
AF x MAMFE
Exemplos
Álgebra de Boole
Procedimento

A
CB 1
F1 D
F3F2
F3 E
F2F1
Análise Top-Down
A = B.C; B = F1+D; D = F2+F3;
C = F3+E; E = F1.F2
A = (F1+D) . (F3+E)
A = F1.F3 + F1.E + D.F3 + D.E
A = F1.F3 + F1(F1.F2) +
F3(F2+F3) + (F2+F3)(F1.F2)
A = F1.F3 + F1.F1.F2 + F2.F3 +
F3.F3 + F2.F2.F1+ F3.F1.F2
Lei Idempotente

Análise Top-Down
A = B.C; B = F1+D; D = F2+F3;
C = F3+E; E = F1.F2
A = (F1+D) . (F3+E)
A = F1.F3 + F1.E + D.F3 + D.E
A = F1.F3 + F1(F1.F2) + F3(F2+F3) +
(F2+F3)(F1.F2)
A = F1.F3 + F1.F1.F2 + F2.F3 + F3.F3 +
F2.F2.F1+ F3.F1.F2
A = F1.F3 + F1.F2 + F2.F3 + F3 + F2.F1+
F3.F1.F2
De acordo com a Lei de Absorção ( ):
F1.F3 + F2.F3 + F1.F2.F3 + F3 = F3. Sendo
assim:
A =A = F3F3 ++ F1F1..F2F2
X+X.Y = X
A
F3
F2F1
F1.F2

Helman Horácio e Andery, Paulo Roberto Pereira. Análise de Falhas -
Aplicação dos Métodos de FMEA – FTA, 156 pgs., Editora Fundação
Christiano Ottoni – Escola de Engenharia da UFMG, Belo Horizonte, 1995.
Rausand, Marvin e Oien, Knut. The Basic Concepts of Failure Analysis
Reliability. Engineering and System Safety. Vol. 53, p. 73-83, 1996
Lafraia, João Ricardo Barusso. Manual de Confiabilidade, Mantenabilidade e
Disponibilidade. 374 pgs, Editora Qualitymark, ISBN 85-7303-294-4, Rio de
Janeiro, 2001.
Seixas, Eduardo de Santana. Construção de Árvores de Falhas. Qualytek -
Qualidade, Tecnologia e Sistemas LTDA, 2001.
Scapin, Carlos Alberto. Análise Sistêmica de Falhas. 131 pgs, Editora de
Desenvolvimento Gerencial, ISBN 85-86948-18-7, Belo Horizonte, 1999.

Mod6 arvore falhas2008

Mais conteúdo relacionado

Mais procurados

Último

Mod6 arvore falhas2008