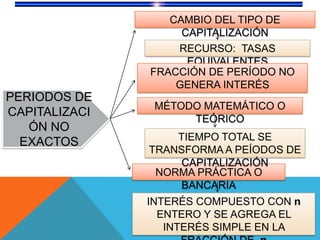
Este documento apresenta exemplos de como calcular juros compostos usando diferentes métodos e taxas de juros. Ele mostra como calcular o montante final aplicando juros semestrais ou mensais a uma quantia inicial de $2.500 durante 22 meses a uma taxa de 6% ao ano.

1. TRABAJO DE ESTADÍSTICA
I N T E G A N T E S : YA D I R A A N D R A D E
ROMEL CAISEDO
GABRIELA JUMA
C AT E D R AT I C O : I N G . L U I S
ANDRADE

2. CAMBIO DEL TIPO DE
CAPITALIZACIÓN
RECURSO: TASAS
EQUIVALENTES
FRACCIÓN DE PERÍODO NO
GENERA INTERÉS
PERIODOS DE
MÉTODO MATEMÁTICO O
CAPITALIZACI
TEÓRICO
ÓN NO
TIEMPO TOTAL SE
EXACTOS
TRANSFORMA A PEÍODOS DE
CAPITALIZACIÓN
NORMA PRÁCTICA O
BANCARIA
INTERÉS COMPUESTO CON n
ENTERO Y SE AGREGA EL
INTERÉS SIMPLE EN LA

3. EJEMPLO: CAMBIANDO LA TASA DE INTERÉS
DETERMINAR EL MONTO DE $2500 DURANTE 22
MESES AL 6% CONVERTIBLE
SEMESTRALMENTE.
Datos: M
2500
M = ??
c = $2500 0 1 2 3 ... 22
n = 22/6
r = 0,06
Cálculo: (1 + r/12)12 = (1 +
0,06/2)3.66
r/12 = (1 + 0,003)3.66
M = c ( 1 + r )n
3.66

4. EJEMPLO: LA FRACCIÓN DE PERIODO NO GENERA
INTERÉS
DETERMINAR EL MONTO DE $2500 DURANTE 22
MESES AL 6% CONVERTIBLE
SEMESTRALMENTE.
Datos: 2500 M
M = ?? 0 1 2 3 ... 18 .. 22
.
c = $2500
n = 3 sem
r = 0,03 sem
Cálculo: M = c ( 1 + r )n
M = 2500 (1 + 0,03)3
M = 2731,8175

5. EJEMPLO: MÉTODO MATEMÁTICO
DETERMINAR EL MONTO DE $2500 DURANTE
22 MESES AL 6% CONVERTIBLE
SEMESTRALMENTE.
Datos: 2500 M
M = ?? 0 ... 22
1 2 3
c = $2500
n = 22/6
r = 0,06
Cálculo: M = c ( 1 + r )n
M = 2500 (1 + 0,03)22/6
M = 2500 (1,114)

6. EJEMPLO: NORMA PRÁCTICA
DETERMINAR EL MONTO DE $2500 DURANTE
22 MESES AL 6% CONVERTIBLE
SEMESTRALMENTE.
M
Datos: 2500
M = ?? 0 ... 18 .. 22
1 2 3
c = $2500 .
n = 3s 4m
r = 0,03 sem
Cálculo: M = c ( 1 + r )n (1 + rt)
M = 2500 (1 + 0,03)3 [1+0,06 (4/12)]
M = 2731,8175 (1,02)