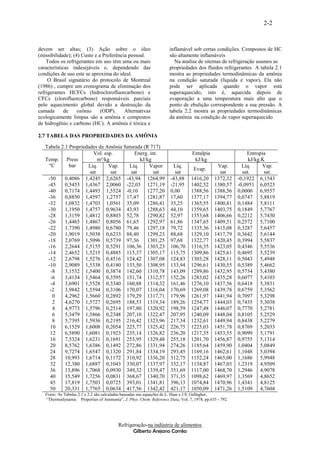
Este documento apresenta um resumo dos principais tópicos abordados no livro "Refrigeração na indústria de alimentos" de Gilberto Arejano Corrêa. O capítulo 1 discute princípios fundamentais de termodinâmica e transferência de calor. Os capítulos subsequentes abordam refrigerantes, ciclos de refrigeração por compressão, sistemas de refrigeração por absorção e psicometria. Os últimos capítulos focam no estudo da carga térmica de alimentos como peixe e frut










![Para um sistema em movimento (aberto), onde pv – energia potencial de fluxo associado ao campo
fica implícita a conservação da energia contida em de forças do escoamento.
um volume de controle, supondo fluxo estacionário. c²/2 – energia cinética.
É calculada mediante: gz – energia potencial gravitacional.
Q W me1 e 2 0
(1.6) Na análise de alguns processos específicos, as
duas últimas parcelas costumam ser negligenciada
A segunda lei da termodinâmica estabelece em presença das demais, de modo que a equação
as condições em que é possível a transformação de (1.6) pode ser rescrita na forma:
calor em trabalho. A conversão de calor em energia
mecânica é conseguida por meio de uma máquina Q W m[u 2 u1 p1v1 p 2 v 2 ]
(1.9)
térmica, cujo enunciado (Kelvin e Planck) pode ser:
É impossível construir uma máquina térmica que, Uma combinação de propriedades
operando em ciclo, transforme em trabalho todo o termodinâmicas ocorre quando temos um processo
calor recebido de uma fonte. à pressão constante que denominamos de entalpia
Como conseqüência da segunda lei da (h) e que é a soma (u+pv), e se dividirmos pela
termodinâmica estabelece o conceito de entropia. A vazão mássica teremos:
entropia se define mediante a seguinte equação:
q w h 2 h1 (1.10)
dQ (1.7)
dS (processo reversível) Onde h = entalpia, em kj / kg; u = energia
T
A entropia procura mensurar a parcela de interna, em kJ / kg; p = pressão, em N/m²; v =
energia que não pode mais ser transformada em volume específico, em m³/ kg. A importância da
trabalho, em transformações termodinâmicas. O entalpia se deve a sua presença em todos os
calor é a forma mais evidente de se fazer a entropia problemas em fluxo estacionário.
do sistema variar (aumentar o micro estado A entropia, como a entalpia, é uma
significa desperdiçar energia que poderia ser propriedade matemática que não é evidente por
aproveitada como trabalho), ao passo que a troca de medições diretas. Em engenharia, a entropia é útil
energia mediante trabalho por si só não implica na solução de problemas que incluem processos
variação da entropia. isotérmicos ou adiabáticos reversíveis. Em
Em sistemas mais complexos, o que inclui as termodinâmica mais avançada, se usa entropia
transformações irreversíveis é quase sempre como um critério de equilíbrio, através de análises
produzida dentro do próprio sistema, e a variação exergéticas.
total na entropia destes sistemas é igual à soma de
dois termos: a entropia produzida e a entropia 1.10 O GAS PERFEITO
trocada com a vizinhança.
A entropia trocada equivale, conforme descrito, Uma equação de estado expressa a relação
à integral de dQ/T, sendo sempre nula quando a entre a pressão, o volume específico e a
transformação é adiabática. Já a entropia produzida temperatura de uma substância. No caso de um gás
vale zero apenas quando o processo é reversível, perfeito:
sendo sempre positiva em transformações
irreversíveis. pv RT (1.11)
1.9 ENERGIA ESPECÍFICA, ENTALPIA E A constante do gás, R, varia para os diferentes
ENTROPIA. gases. A equação (1.11) é satisfatória para gases
reais a relativamente altas temperaturas e baixas
Como resultado da primeira lei da pressões; em cálculos do ar úmido este se comporta
termodinâmica, obtivemos o conceito da como um gás perfeito.
propriedade de energia interna. A energia Para os gases perfeitos podemos deduzir
específica do escoamento (Eq. 1.8) inclui todos os muitas relações que incluem calores específicos.
tipos de energia armazenadas em suas moléculas Para qualquer processo, podemos provar que a
energia interna é função só da temperatura e é
expressa por:
c2
e u pv gz (1.8)
2 u 2 u1 cv t 2 t1 (1.12)
Onde temos:
u – energia interna (devido ao movimento e/ou
forças intermoleculares).](https://image.slidesharecdn.com/livrorefri-120915130244-phpapp02/85/Livro-refri-11-320.jpg)







![2-7
cristalização (gelo) das salmouras ou dos
2.8 REFRIGERANTES SECUNDÁRIOS anticongelantes.
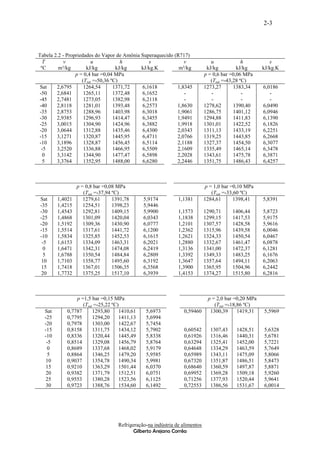
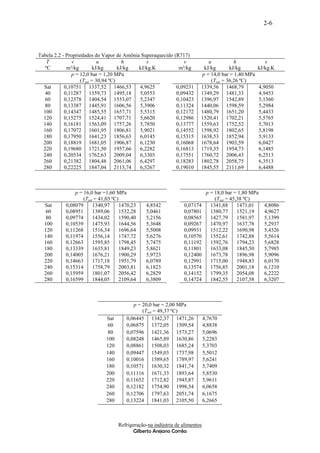
A Figura 2.3, 2.4 e 2.6, mostra o diagrama de
São os que não apresentam mudança de fase fase da solução salina, da variação da densidade
durante a troca térmica. Transferem energia da relativa e da variação do calor específico,
substância que está sendo resfriada para o separador respectivamente.
de um sistema de refrigeração.
A Figura 2.2 mostra um ciclo de refrigeração, onde Salmoura
a a carga térmica é removida indiretamente. % em massa de cloreto de Cálcio em água
0
Ponto de Solidificação [ºC]
0 10 20 30 40
-10
-20 líquido
líquido e gelo
-30
líquido e
-40 sal
Sólido E
-50
Figura 2.3 Diagrama de fase
No diagrama de fase mostra as curvas formadas
pelos pontos de congelamento na medida em que
Figura 2.2 Refrigeração indireta
varia a concentração. O ponto E da curva se chama
Ponto Eutético, e representa a concentração a qual
Os principais refrigerantes secundários : Água ;
pode-se alcançar a mais baixa temperatura, sem a
Salmouras (Cloreto de cálcio e de sódio) e os
solidificação total da salmoura.
Anticongelantes (Água+ etileno glicol, ou cloreto de
cálcio, ou alcool, ou glicerina). Seus pontos de
solidificação variam com sua concentração Salmoura
percentual em massa. 1,4
Densidade relativa 15/15ºC
1,35
1,3
2.9 FATORES A CONSIDERAR NA 1,25
ESCOLHA DE UM REFRIGERANTE 1,2
1,15
SECUNDÁRIO
1,1
1,05
- Baixa viscosidade 1
- Calor específico e condutividade térmica alta; 0 5 10 15 20 25 30 35 40
- Não deve congelar-se às temperaturas mais baixas % em massa de cloreto de Cálcio em água
do processo.
Figura 2.4 Variação da densidade
- Segurança operacional.
- Custo e a Preferência pessoal.
A Figura 2.4 mostra para a variação da solução,
valores maiores de densidade relativa do que para a
A água líquida é usada como refrigerante
água pura na mesma temperatura (15ºC).
secundário em instalações de ar condicionado e de
refrigeração em processos industriais, onde as
condições de temperatura estejam acima do seu ponto Salmoura
de congelamento. Devido a sua fluidez, alto calor
4,5
Calor específico kJ/kg.K
específico e coeficiente de troca térmica 4
(condutividade e convecção) é excelente podendo ser 3,5
utizada em resfriadores do tipo Chillers, ou de forma 3
2,5
pulverizada.
2
A água líquida na temperatura do seu ponto de 1,5
congelamento ocorre a sua cristalização (gelo). A 1
adição de sais e glicóis dissolvidos a água forma as 0 5 10 15 20 25 30 35 40
salmouras e os anticongelantes respectivamente. Em % em massa de Cloreto de Cálcio em água
princípio quanto mais alta for a concentração (de sais
Figura 2.5 Variação do Calor específico
ou glicóis), mais baixa é a temperatura da
Refrigeração-na indústria de alimentos
Gilberto Arejano Corrêa](https://image.slidesharecdn.com/livrorefri-120915130244-phpapp02/85/Livro-refri-24-320.jpg)
![2-8
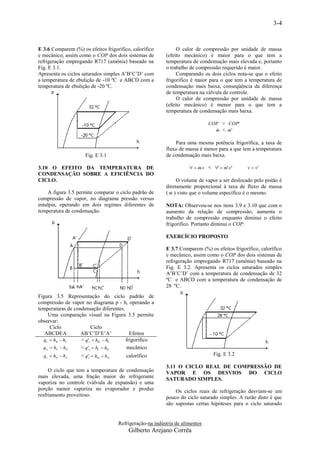
A Figura 2.5, mostra para a solução valores b) Se a salmoura se esfria a -40ºC, qual é o
menores do calor específico, quando comparados percentual em peso da solução, se transformará em
com a água pura. gelo e em líquido?
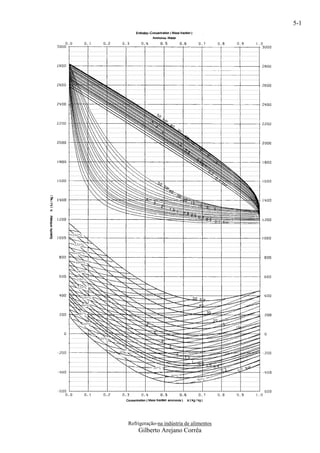
O principal objetivo das salmouras e dos Solução:
anticongelantes é permitir que as soluções tenham a Com o auxílio do diagrama de fase (Fig. 2.3) e com
temperatura do ponto de congelamento menor que o 25% em peso de cloreto de cálcio, traço uma linha
da água pura. auxiliar até a temperatura de -40ºC. Obtenho duas
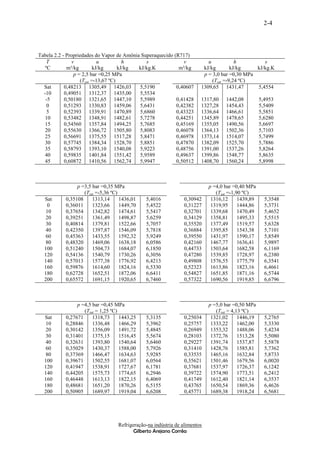
A Figura 2.7, mostra o diagrama do ponto de áreas, onde x1 é a parcela líquida e x2 é a parcela de
congelamento versus percentual de concentração em gelo.
massa, de algumas soluções salinas e glicóis. Salmoura
% em massa de cloreto de Cálcio em água
0
Ponto de Solidificação [ºC]
0 10 20 30 40
-10
-20 líquido
líquido e gelo
-30 l
x1 l x2 líquido e
-40 sal
l E
Sólido
-50
Assim conforme diagrama de fase : x1 = 25 e x2 =
2,5
x2
% de gelo 100
x1 x 2
2,5
% de gelo 100 = 9,09
25 2,5
Resposta % de gelo = 9,09
% de líquido = 100 - 9,09 = 90,91
Resposta % de líquido = 9,09
E.2.4 Repita o E 2.3 para outras soluções aquosas da
Fig. 2.7.
Figura 2.7 Diagrama do Ponto de congelamento de
soluções aquosas 2.10 AMÔNIA (NH3) – R717
EXERCÍCIOS Devido a sua grande disponibilidade e menor
custo, a amônia tem se imposto como preferido, na
E 2.1 Se a amônia a 100 kPa tem uma temperatura seleção dos fluidos refrigerantes utilizados nas
real de -30 ºC, o seu estado pode ser descrito como: instalações frigoríficas industriais a mais de 120
a) Superaquecida; b) Subresfriada e c) Saturada. anos.
Solução Propriedades da amônia
Conforme Tabela 2.2 para a pressão de 100 kPa (ou 1 A Tabela 2.3 mostra algumas propriedades da
bar) a temperatura de saturação é Tsat =-33,60 ºC amônia
Como - 30 ºC > Tsat (Figura 1.0) o estado é Tabela 2.3 Propriedades da amônia
superaquecido. Resposta a) Cor Incolor
Odor Forte, irritante
E 2.2 Determinar a entalpia (h) da amônia do E 2.1. Peso molecular 17,03
Solução. Ponto de ebulição a 1bar -33,35 ºC
Conforme Tabela 2.2 Resposta h = 1406,44 kJ/kg Ponto de congelamento a 1 bar -77,7 ºC
Calor de fusão 452,8 kJ/kg
E 2.3 Uma solução de 25% em peso de cloreto de Calor de vaporização a 1 bar 1370,33 kJ/kg
cálcio (CaCl2) em água se esfria gradualmente. Temperatura crítica 132,4 ºC
a) A que temperatura começa a cristalização? Pressão crítica (absoluta) 111,5 bar
Solução: Com o 25% no diagrama de fase, o ponto de Densidade crítica 0,235 kg/l
congelamento é -30ºC Resposta T= -30 ºC Fonte: FCI Chemical Engineers, 1989.
Refrigeração-na indústria de alimentos
Gilberto Arejano Corrêa](https://image.slidesharecdn.com/livrorefri-120915130244-phpapp02/85/Livro-refri-25-320.jpg)































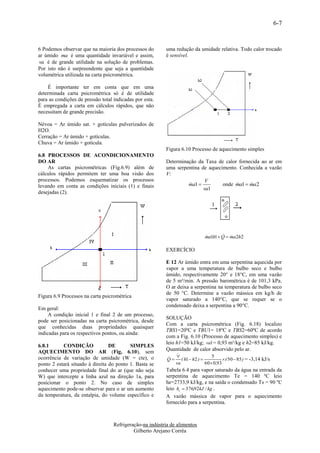

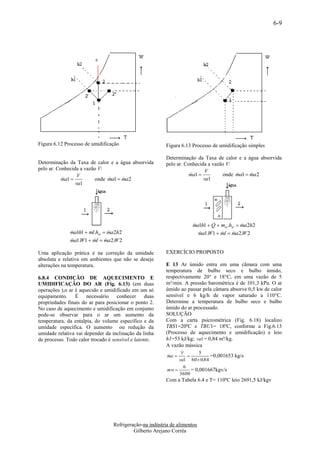
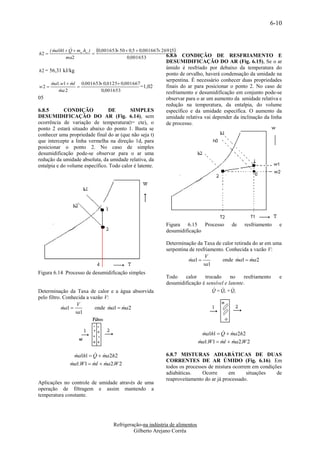
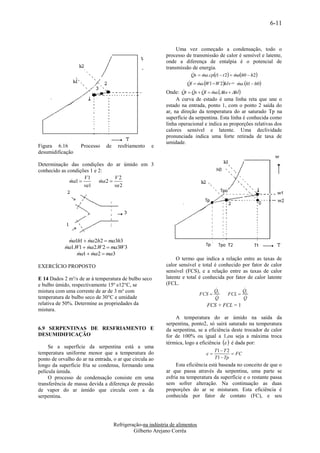








![7-5
temperaturas Ti e Tm , f são assumidas como valores
de condição de equilíbrio térmico do sólido, no EXERCÍCIO
tempo inicial e final. E 7.7 Determinem a quantidade de calor devido a
ocupação, de 2 pessoas na movimentação de carga,
EXERCÍCIO durante 0,25 horas/dia em uma câmara a -18ºC.
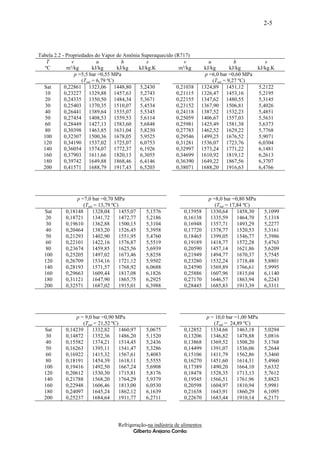
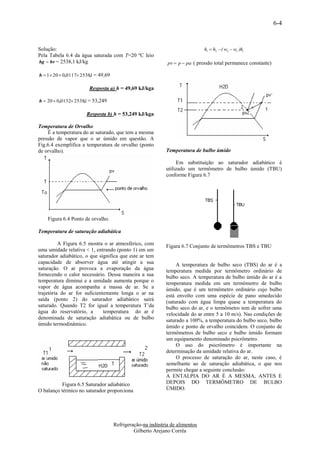
E 7.6 Determinem a quantidade de calor removido no SOLUÇÃO
congelamento de 20 tonelada de peixe (magro) de - Com a tabela 7.5 e a temperatura leio o fator de
0,8 ºC (início de congelamento) a -18 ºC por dia calor/pessoa, F = 1400 kJ/h
sendo conhecida a variação da entalpia (Fig. 7.2)
30
Qpessoas 1400 2 0,25 = 700 kJ/dia
25
Hgcastanha
20 7.6 CARGA TÉRMICA DE MOTORES
hmf, hi [kJ/kg]
Hfcastanha
ELÉTRICOS EM UMA CÂMARA
15 FRIGORÍFICA
10
Os motores elétricos querem estejam no recinto,
5
em qualquer ponto do fluxo de ar ou mesmo nos
ventiladores, adicionam carga térmica ao sistema
0 devido às perdas nos enrolamentos, e esta carga
-20 -16 -12 -8 -4 0 precisa ser retirada pela instalação frigorífica. É
T [ºC] preciso levar em conta se o motor está sempre em
Figura 7.2 Variação da entalpia na temperatura funcionamento ou se a sua utilização é apenas
média ( hm ) e a do início do congelamento ( h g ) do esporádica.
peixe magro. As vazões do ar dos ventiladores, na refrigeração
Qproduto m hi hm , f 20000 ( 25,12 4,10 ) de produtos, apresentam uma circulação de 60 a 80
Calor a ser removido por dia é 420 400 kJ/dia vezes por hora o volume da câmara (ou túneis) vazia.
Esta condição permite velocidades de 0,5 a 2 m/s
7.5 CARGA TÉRMICA DE OCUPAÇÃO POR junto ao produto dependendo do lay out.
DIA DE PESSOAS EM UMA CÂMARA No congelamento as vazões do ar dos
FRIGORÍFICA ventiladores, apresentam uma recirculação de 100 a
150 vezes por hora o volume da câmara (ou túneis)
A Tabela 7.5 mostra o desprendimento de calor vazia. Esta vazão permite velocidades do ar
de uma pessoa adulta executando forte trabalho aproximadas de 3 m/s junto ao produto.
Comercialmente se usa motores de potência ( W )
corporal. Para trabalhos médios podemos considerar
a metade do valor do fator equivalente desta tabela. de 0,5 CV para cada 6000 m³/h insuflados por
resfriadores de ar forçado.
nº de horas de ocupação
Q pessoas Fator nº de pessoas
dia W
Qmotores
736 [kJ/dia]
motor
Tabela 7.5 Fator equivalente Onde
de Calor/Pessoa é o número de horas de funcionamento do
Temperatura Fator motor;
ambiente em ºC em kJ/h
10 760 motor é o rendimento do motor.
5 890
-1 1000 Tabela 7.6 Rendimento do motor
-7 1100 motor
W
-12 1300
-18 1400 < ½ CV 0,6
-24 1500 ½ a 3 CV 0,68
-30 1600 3 a 20 CV 0,85
-36 1680
-42 1800 EXERCÍCIO
-48 1900
Refrigeração-na indústria de alimentos
Gilberto Arejano Corrêa](https://image.slidesharecdn.com/livrorefri-120915130244-phpapp02/85/Livro-refri-73-320.jpg)

![7-7
capítulos seguintes apresentam as características de
alguns alimentos.
EXERCÍCIO
E 7.12 Determinem a carga térmica total, QT , do
exercício E 7.10, considerando a vazão de ar de 1610
m³/dia do exercício E 7.3.
SOLUÇÃO
Carga térmica cedida:
Paredes 133804 kJ/dia 18,3%
Ar 152272 kJ/dia 20,9%
Produto 420400 kJ/dia 57,6%
Pessoas 700 kJ/dia 0,1%
Motores 20782 kJ/dia 2,8%
Iluminação 1575 kJ/dia 0,2%
Total 729533kJ/dia 100,0%
Com o Fator de segurança de 10%
QT 1,1 729533kJ/dia 8024863 kJ/dia
,
Resposta Q 8024863 kJ/dia
,
T
E 7.13 Determinem a capacidade frigorífica
requerida, QE , pela carga térmica, QT , do exercício
E 7.12. Considere que toda a operação da troca
térmica ocorra em 18 h
kJ dia h
QE 8024863
, 12,38405kW
dia 18h 3600s
Resposta Q 12,4kW
E
E 7.14 Determinem o tempo em horas na remoção de
calor do exercício E 7.12 utilizando a capacidade
frigorífica de 15 kW do E 7.11.
SOLUÇÃO
O tempo necessário para remover a taxa de calor
QT 8024863 kJ/dia
,
18h 12,4kW
tempo 14,9h
15kW
Resposta tempo = 14,9h
REFERÊNCIA
[5] - DOSSAT, R.J. - Manual de Refrigeração - Ed.
Hemus - São Paulo, 1980.
[2] - PHOLMANN, W. - Manual de Técnica
Frigorífica - Ediciones Ômega, S.A. - Barcelona,
1964.
Refrigeração-na indústria de alimentos
Gilberto Arejano Corrêa](https://image.slidesharecdn.com/livrorefri-120915130244-phpapp02/85/Livro-refri-75-320.jpg)



![8-4
variação da taxa de calor removida foi utilizado o
método analítico para problemas de condução E 8.8 Determinem o perfil da taxa de calor
transiente, obtida da solução da equação da condução removida do peixe do E 8.7
de calor, tridimensional, aplicada a paralelepípedo. Dados utilizados na simulação:
Peso do peixe inteiro m = 0,9 kg
A temperatura média com o tempo é obtida da
1,8
equação
1,6
Q
m, f 1
x y z dV
1,4
i
m, f
V
Q [kW]
1,2
Substituindo as soluções de , , e resolvendo
x y z 1
a integral é determinada a temperatura média Tm,f . 0,8
m,f n sen( n x ) n
sen( n y )
n sen n ( n z )
0,6
Cn . Cn
i
n1 2
n exp n Fo x n1
n exp n Fo
2
. C
y n1
n
2
n exp n Fo z
0,4
0,2
Onde 100 200 300 400 500 600 700 800 900 1000
m , f Tm , f T0 e i Ti T0 sendo ,f
m f Fo,Bi . tempo [s]
Através do Fo para cada Tm , f desejado teremos o O perfil da taxa de calor é o calor removido
tempo decorrido para atingir esta temperatura. (obtido como no exercício E 8.3) em um intervalo
de tempo.
8.6 PROGRAMA COMPUTACIONAL Assim:
1)Conhecendo a capacidade frigorífica, QE , da
As equações foram resolvidas numericamente câmara (ou túnel) para a tca= -23 ºC, e os perfis
utilizando as propriedades termofísicas (massa dos exercícios E 8.7 e E 8.8, posso determinar a
específica, calor específico, difusividade térmica, movimentação e a quantidade de peixes.
condutividade térmica e entalpia) do alimento obtidas 2)Conhecendo os perfis dos exercícios E 8.7 e E
em função da temperatura média do volume no 8.8, a movimentação e a quantidade de peixes.
tempo. Podemos determinar a capacidade frigorífica,
Foram desenvolvidos programas computacionais
QE , da câmara (ou túnel) para a tca= -23 ºC.
para auxiliar a predição das propriedades termofísicas
e de tempos de congelamento de alimentos. A
utilização destes, e sua combinação permitiram a
determinação dos perfis de temperaturas no centro, REFERÊNCIAS
superfície e média dos alimentos.
ASHRAE HANDBOOK. Refrigeration systems
E 8.7 Determinem o perfil de temperatura no and applications. Atlanta: American Society of
congelamento de peixe eviscerado sem cabeça e calda Heating. Refrigeration and Air-Conditioning.
da espécie castanha. Engineers, 1998.
Dados utilizados na simulação: COSTA, Ê. C., Refrigeração. 3° ed. Edgard
Troca térmica tridimensional em regime transitório. Blücher LTDA. São Paulo, 1994.
Temperatura da câmara tca = -23 ºC, = 90% e DOSSAT, Manual de Refrigeração. HEMUS, vol
2 e 4. Houston, 1980
velocidade do ar de 2 m/s.
INCROPERA, F.P. & WITT, D.P. fundamentos
-5 da Transferência de Calor e de Massa,
Guanabara. Rio de Janeiro, 1992.
-8,5
tMÉDIO PLANK, R. El Empleo del Frío en la Industria de
tCENTRO
la Alimentación, Reverté S.A. Barcelona
Espanha, 1963.
tMÉDIO, tCENTRO
-12
STOECKER, W.F. Refrigeração e Ar
-15,5 Condicionado. Mc Graw Hill. São Paulo, 1985.
RUSCHEINSKY,NIRSE.Refrigeração de filé de
-19
pescado.
BONACINA, MARLICE.Desenvolvimento e
-22,5
Caracterização de Empanado a partir da Corvina.
100 200 300 400 500 600 700 800 900 1000
tempo [s]
Refrigeração-na indústria de alimentos
Gilberto Arejano Corrêa](https://image.slidesharecdn.com/livrorefri-120915130244-phpapp02/85/Livro-refri-79-320.jpg)




![10.2
- O armazenamento dos materiais deve ser adequado, menor temperatura. Os mecanismos desta
em ambiente seco e fresco, tanto antes de começar o transferência de calor ocorrem por condução,
serviço, como durante a obra. convecção e radiação. A combinação dos
- Verificar a segurança dos andaimes a fim de evitar mecanismos conveção e radiação ocorrem
acidentes. normalmente em paralelo.
- Os objetos isolantes deverão ter as superfícies Todos os cálculos apresentados prevêem
limpas, bem como as áreas a serem isoladas. Deverão condições de transferência de calor em estado
ser eliminadas, também, irregularidades da superfície. estacionário.
- Os isolantes devem ser medidos e conferidos no ato
A perda térmica ou taxa de calor, Q , é dada
do recebimento, e somente deverão ser aceitos se por:
estiverem rigorosamente dentro das especificações.
T
Q (10.1)
10.3 RECOMENDAÇÕES PARA REDUZIR A Rt
TEMPERATURA EM CÂMARAS
FRIGORÍFICAS. A resistência térmica total, Rt é o somatório
das resistências: convecção interna e externa,
Após a conclusão da construção de uma câmara: condução das paredes compostas e radiação interna
- Somente iniciar o processo de resfriamento após ter e externa.
passado 15 dias do lançamento do concreto da lage
superior do piso (acabamento); R t R convec. R cond. R rad. (10.2)
- Resfriar a câmara até +2ºC/+3ºC, a razão de 5ºC por
dia;
10.5.1 Condução
- Manter a temperatura em +2ºC/+3ºC durante seis
dias;
A lei fundamental que descreve a condução
- Abaixar a temperatura para -2ºC/ 0 ºC e mantê-lo
térmica é a lei de Fourier (Eq. 10.3).
durante cinco dias;
- Reduzir até a temperatura de trabalho à razão de 5ºC
por dia. k A
xi
Q cond. i i T j T j 1 (10.3)
Observação: O mesmo processo é válido para x espessura do material [m]
câmaras frigoríficas que já estavam em operação, mas A área normal a transferência de calor [m²]
que foram aquecidas para trabalho de manutenção. k coeficiente de condutibilidade térmica [W/m.K]
j volume de controle entrada e saída
10.4 COMO EVITAR O CONGELAMENTO DO
SOLO SOB CÂMARAS FRIGORÍFICAS. Onde k é uma propriedade própria de cada material
(i). Consiste numa grandeza física que mede a
Depende do solo e do lençol freático e linha capacidade de uma substância conduzir o calor. A
isotérmica zero, no interior do isolamento. Deve-se Tabela 10.1 classifica os materiais através da
empregar isolamento de boa qualidade e mais as condutividade térmica.
seguintes providências:
A resistência térmica por condução
- Construir a unidade frigorífica sobre uma camada de x
pedra britada com espessura não inferior a 60 cm; Rcond. i (10.4)
k i Ai
- Concretar a laje do contrapiso sobre canais de
ventilação;
- Elaborar o projeto arquitetônico de materiais tais a Tabela 10.1 Classificação dos materiais na
se ter entre a laje do contrapiso e do solo, um vão condução de calor.
livre de 60 cm, que permitirá uma ventilação natural; Classificação k [W/m.K]
- Instalar um sistema de aquecimento do contrapiso. Condutores >23
Semi-condutores 9 a 23
10.5 ISOLAMENTO DE PAREDES PLANAS Refratários 1,1 a 3,5
Refratários leves 0,35 a 1,1
Toda parede a uma temperatura inferior a do Semi-refratários 0,16 a 0,35
ambiente, como a de câmaras frigoríficas, devem ser Isolantes <0,16
isoladas para reduzir as perdas térmicas e evitar a
condensação superficial. A Tabela 10.2 mostra a condutibilidade de alguns
A transferência de calor ocorre na existencia de Materiais.
regiões a diferentes temperaturas, no sentido das de
Refrigeração-na indústria de alimentos
Gilberto Arejano Corrêa](https://image.slidesharecdn.com/livrorefri-120915130244-phpapp02/85/Livro-refri-85-320.jpg)
![10.3
Tabela 10.2 Condutibilidade de alguns A resistência térmica convectiva
materiais 1
Material k [W/m.k] R convec. (10.6)
h cj A j
Aço 45
Concreto 1,3 A Tabela 10.3 mostra valores práticos do
Gelo 1,9 coeficiente, hc.
Argamassa 0,6
Tijolo 0,4 - 0,8 Tabela 10.3 Convecção de alguns sistemas
Asfalto 0,6 Sistemas hc [W/m2.k]
Fibra de vidro 0,046 Natural - gás 2 - 15
Ar parado 0,026 Forçado - gás 15 - 250
Poliestireno 0,028-0,035 Natural - líquidos 50 - 1000
Poliuretano 0,017-0,020 Forçado - líquidos 1000 - 100000
E 10.1 Determinem a taxa de calor por condução, de O coeficiente, hc é determinado através de
uma parede de poliestireno (k = 0,035 W/m.K) com estudo do escoamento através de vários trabalhos
espessura x igual a 100 mm, sujeita a uma diferença numéricos e experimentais, encontrados na
de temperatura ΔT igual a 30ºC. Compare com o literatura.
valor obtido da Tabela 7.1.
Solução: 10.5.3 Radiação
Fazendo A = 1 m², determinamos a resistência
térmica da parede. A energia radiante que um corpo emite
x 0,1 K (Eq.10.7) é dada pela Lei de Stefan-Boltzmann
R 2,857143 aplicada a um corpo real.
k A 0,035 1 W
Rearanjando a Eq.(10.1), determinamos a taxa de
calor Q rad . A j Tsup . T.
4 4
(10.7)
Q T 30 W kJ
10,5 907
Q rad. h r A j Tsup . T (10.8)
A R.A 2,857143 m2 m 2 dia
O valor da taxa de calor obtido pela Tabela 7.1 é de coeficiente de radiação térmica [W/m².K]
hr
904,1 kJ/m²dia. Comparando a diferença dos valores A área normal a transferência de calor [m²]
em relação ao da Tabela 7.1 j volume de controle entrada e saída
907,2 904,1
Dif % 100 0,34% (maior)
904,1 A resistência térmica radiante
Comentário: O valor tabelado fornecido pelo 1
R radiação (10.9)
fabricante é confiável. h rj A j
onde o coeficiente de transferência de calor por
radiação
10.5.2 Convecção
h r . Tsup . T Tsup . T
2 2
(1.32)
A Eq. (10.5) é conhecida como lei de Newton. O
calor se transmite por partículas do meio, que se Onde “σ” é a constante de Sefan-Boltzmann e vale
movimentam de um local para outro. Ocorre com 5,6697E-8 W/(m²K4) onde a emissividade (ε) é uma
líquidos e gases de duas maneiras: propriedade radioativa da superfície. A Tabela
- Convecção natural (ou convecção livre) quando o (10.4) mostra os valores da emissividade e da
movimento se deve a diferença de densidade. absortividade (α) de vários superfícies onde α= ε.
- Convecção forçada quando o movimento é
provocado por agentes externos ( ventoinha, agitador Tabela 10.4 Emissividade (ε) e Absortividade (α)
e bomba). Emissividade ou
Superfícies absortividade
Q convec. h cj A j Tsup . T (10.5)
Cor negra
10 - 35ºC
0,90 a 0,98
500ºC
0,90 a 0,98
Pintura escura 0,85 a 0,95 0,75 a 0,90
hc coeficiente de convecção térmica [W/m².K] Pintura clara 0,85 a 0,95 0,70 a 0,85
A área normal a transferência de calor [m²] Pintura branca 0,85 a 0,95 0,60 a 0,75
j volume de controle entrada e saída Pintura alumínio 0,40 a 0,60 -
Refrigeração-na indústria de alimentos
Gilberto Arejano Corrêa](https://image.slidesharecdn.com/livrorefri-120915130244-phpapp02/85/Livro-refri-86-320.jpg)
![10.4
Quando ocorem simultâneamente a transferência x isolameno
de calor simultânea por convecção e radiação, utiliza- R isolamento
k isolamento A isolamento
se um coeficiente combinado (h’ = hc + hr)
Ou seja
10.6 CÁLCULO PRÁTICO DE ESPESSURA DE x isolamento R isolamento k isolamentoA isolamento
ISOLAMENTO TÉRMICO
x isolamento 4,817143 * 0,035 *1 0,1686 m
O cálculo da espessura, a partir de uma taxa de
calor estimada por unidade de área, conduz a Comentário:
resultados rápidos. Este método garante uma taxa de - Ao considerar Ra = 0 simplifica os cálculos e
calor, dentro de uma classificação (Tabela 10.5) de garante um fator de segurança.
qualidade aceito internacionalmente. - A colocação de duas camadas de espessura
comercial (100mm + 75mm) com as juntas
Tabela 10.5 Classificação do isolamento em desencontradas na horizontal e vertical satisfaz a
relação a taxa de calor por unidade de área espessura de 169 mm e garante um fator de
ótimo < 9,3 W/m² segurança.
9,3 ≤ bom ≤ 11,7 W/m²
11,7 ≤ regular ≤ 17,4 W/m²
10.6 CÁLCULO DO ISOLAMENTO
EXERCÍCIO TÉRMICO PARA QUE NÃO OCORRA
CONDENSAÇÃO SUPERFICIAL
E 10.2 Determinem a espessura do isolante térmico
(poliestireno) para uma uma parede de alvenaria, para A condensação da umidade do ar
que seja admitida uma perda máxima Q A = 9 W/m² atmosférico ocorre quando a mesma atinge valores
nas seguintes condições: Tint.=-10ºC e Text.=35ºC inferiores a sua temperatura de orvalho, ponto de
respectivamente temperaturas interna e externa da saturação. O ar em contato com uma parede fria,
parede. diminui sua temperatura podendo condensar sobre a
Considerar: mesma.
- A transferência de calor combinada (h = hc + hr)
externa hext. = 25 W/m²K e interna hint. = 7 W/m²K E 10.3 Determinem a espessura limite do
obtida da Tabela 10.3. isolamento térmico para que não ocorra
- Estado estacionário (Text. a Tint. constantes no tempo) condensação superficial em um frezer, sabendo que:
- Resistência térmica da alvenaria Ra = 0 (valor pouco 1) Temperaturas: do ar externa 30ºC e U.R. 80%;
significativo) da parede interna -20ºC.
2)Coeficientes: kisol. = 0,02 W/m.ºC e har = 20
Solução W/m².ºC
1 1
R combinado Solução:
' A ' A
h ext . ext . h int . int .
Fazendo as áreas iguais a 1 m². Determinação da temperatura do ponto de orvalho
do ar:
1 1
R combinado 0,182857 [K / W] Com Text.=30ºC, obtemos da Tabela (6.4) de
25x1 7 x1 saturação da água , a pressão de saturação ps =
Rearanjando a Eq.(10.1), determinamos a taxa de 0,042460 bar.
calor
Q T A pressão de vapor do ar (pv): p v (U.R.).p s
A (R combinado R isolamento )A
T p v 0,8 0,042460 0,033968 bar
R isolamento R combinado
Q Consultando a mesma Tabela (6.4), com p v na
( )A condição de saturado determino a temperatura de
A
saturação do ar (para 30ºC e 80% de umidade
A isolamento igual a 1m² normal ao sentido da taxa relativa) Ts= 26,06ºC. A temperatura de orvalho,
de calor. To, corresponde a temperatura de saturação T s.
(35 (10))
R isolamento 0,182857 4,817143 [K / W]
(9) x1 To= 26,06ºC (Temperatura de orvalho)
Conforme Eq.(10.4)
Determinação da taxa de calor
Refrigeração-na indústria de alimentos
Gilberto Arejano Corrêa](https://image.slidesharecdn.com/livrorefri-120915130244-phpapp02/85/Livro-refri-87-320.jpg)


![10.7
Resistência a passagem de calor
La Li O prazo de retorno é o espaço de tempo
R Ra Ri
(10.14)
ka A kiA necessário para que os Benefícios B advindos do
investimento possam cobrir seus Custos C,
considerados a uma adequada taxa de juros, ou seja,
Lm (m) Ra [K/W] Ri [K/W] R [K/W] quando C - B = 0.
0,05 0,00357 0,01667 0,02024 Para uma melhor compreensão utilizaremos
0,10 0,00357 0,03333 0,03690 uma representação gráfica (Fig.10) que permite
0,15 0,00357 0,05000 0,05357 visualizar as posições econômicas ao longo do
0,20 0,00357 0,06667 0,07024 tempo denominado Fluxo de Caixa.
0,25 0,00357 0,08333 0,08690 Consideremos um fluxo de caixa em que o
Benefício ou Receita é a economia do Custo de
Custo das perdas térmicas para cada espessura Produção Frigorífica durante o prazo de retorno n’,
do isolamento onde a economia é a diferença entre o custo de
Lm r T R CP Produção Frigorífica com e sem isolamento.
(m) [R$/Wano] [K] [K/W] [R$/ano]
0,05 5,136 50 0,02024 12688,94 F
0,10 5,136 50 0,03690 6958,45 A1 - A2
0,15 5,136 50 0,05357 4793,60
0,20 5,136 50 0,07024 3656,14 0
0,25 5,136 50 0,08690 2954,96
1 2 3 4 n'
P
O custo total CT é a soma do custo do isolamento
amortizado CI e do custo das perdas térmicas CP Figura 10.3 - Fluxo de Caixa na obtenção do prazo
de retorno
Lm CA CP CT Convenções adotadas no diagrama do Fluxo de
(m) (R$/ano) (R$/ano) (R$/ano) Caixa:
0,05 2716,02 12688,94 15404,96 1. O eixo horizontal representa o tempo a partir de
0,10 5432,04 6958,45 12390,49 um instante considerado inicial até um instante
0,15 8148,06 4793,60 12941,66 considerado final do prazo em questão.
0,20 10864,09 3656,14 14520,23 2. Os segmentos positivos, isto é, do eixo horizontal
0,25 13580,11 2954,96 16535,07 para cima, representam: a economia (A1-A2) e o
Valor Residual (F) do isolamento.
O custo total mínimo indica 0,10 m como a 3. O segmento negativo, isto é, do eixo horizontal
espessura térmica econômica para 10 anos de vida para baixo, representa o valor do investimento (P)
útil. do isolamento.
Analisando pelo Método do Prazo de Retorno
A Figura 10.2 mostra a curva de custos para do Investimento, em função do Valor Presente
diferentes espessuras. Líquido (VPL) e avaliando-se o valor da venda
residual para o instante n' considerado,
verificaremos se devemos investir no isolamento
Camortizado Cptérmica C total
(Hirschfeld, 1984):
18000
16000
VPL P (A1 A2)( P / A, i%, n' ) F(P / F, i%, n' ) 0
14000
(10.15)
Custo [R$]
12000
10000
8000 A última parcela da Eq. (10.15), representa o
6000
valor residual do isolamento e, será considerada
4000
2000 igual a zero por não ter valor de comercialização,
0 ou seja não contribui neste caso para o retorno do
0 0,1 0,2 0,3 investimento. O valor de n’ é calculado
Espessura do isolamento [m] iterativamente de forma que a Eq. (10.15) seja
satisfeita. Se n’ (prazo de retorno do investimento)
Figura 10.2 Curva de custos para diferentes
for menor que n = 10 anos (vida de serviço do bem
espessuras.
investido), o bem deve ser adquirido.
Retorno do investimento a taxas de atratividade.
Refrigeração-na indústria de alimentos
Gilberto Arejano Corrêa](https://image.slidesharecdn.com/livrorefri-120915130244-phpapp02/85/Livro-refri-90-320.jpg)

