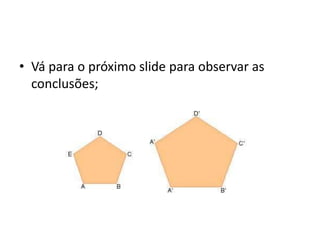
1) O documento explica a fórmula para calcular a bissetriz externa de um ângulo, dada a razão entre os lados do triângulo. 2) Dois polígonos são semelhantes quando têm ângulos correspondentes congruentes e lados correspondentes proporcionais. 3) A razão entre os perímetros de dois polígonos semelhantes é igual à razão entre quaisquer lados correspondentes.

1. CONTEÚDO/ GEOMETRIA
Por: Germano

2. TEOREMA DA BISSETRIZ EXTERNA

3. • O teorema da bissetriz externa possui uma
fórmula simples. De acordo com a figura
anterior:
• 14+x/12 = x/8
• 12x = 112 + 8x
• 4x = 112 x = 112/4
• X = 28 BE = 14+28 BE=42

4. Polígonos Semelhantes
• Dois polígonos são semelhantes quando os
ângulos correspondentes são congruentes e
os lados correspondentes são proporcionais.

5. Propriedade dos Polígonos
Semelhantes
• Se dois polígonos são semelhantes, a divisão
entre seus PERÍMETROS é igual à divisão entre
as medidas de dois lados correspondentes
quaisquer dos polígonos.
• VÁ PARA O PROXIMO SLIDE PARA APRENDER
NA PRÁTICA;

6. • Vá para o próximo slide para observar as
conclusões;

7. • Supondo que o perímetro do primeiro
polígono seja representado como X e o
perímetro do segundo polígono com Y:
De acordo com a figura do slide anterior, temos:
• X/Y = AB/A’B’ = EA/A’A’ = ED/A’D’ = DC/ D’C’ = BC/B’C’
Ou seja, a razão entre os perímetros dos dois polígonos é
igual as medidas dos lados correspondentes;

8. Teorema Fundamental da Semelhança
• Observe atentamente a imagem:
• Conclusões: AE/AB = AD/AC = ED/BC