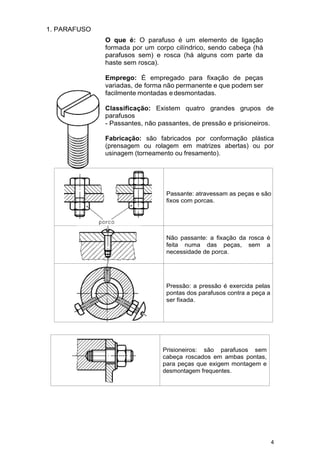
1. O documento descreve cálculos simplificados para dimensionar parafusos. 2. É apresentada a classificação, tipos e aplicações de parafusos. Também são descritas roscas, passo, entradas e direção. 3. Exemplos resolvidos mostram como calcular o diâmetro de parafusos para aguentar cargas em placas, considerando tensão admissível e número de parafusos.

1. INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DE
SANTA CATARINA
DEPARTAMENTO ACADÊMICO DE METAL MECÂNICA
CURSO TÉCNICO EM MECÂNICA
Cálculo Simplificado de Parafusos
Prof. Eng. Mec. Norberto Moro
Téc. Em Mec. Charles Aguiar May
FLORIANÓPOLIS – junho de 2017

2. 2
SUMÁRIO
1. PARAFUSO ..................................................................................................4
1.1 ROSCAS...................................................................................................6
1.1.1 PASSO DA ROSCA ...........................................................................7
1.1.2 ENTRADAS DAS ROSCAS................................................................7
1.1.3 DIREÇÂO DA ROSCA........................................................................7
1.2 DIMENSIONAMENTO DO PARAFUSO ...................................................8
1.2.1 CÁLCULO SIMPLIFICADO ................................................................8
2. REFERÊNCIAS BIBLIOGRÁFICAS.............................................................22

3. 3
SIMBOLOGIA
A Área
F Força
M Momento
R Reação
Sg Coeficiente de Segurança
σ Tensão Normal
σadm Tensão admissível
σe Tensão de escoamento
∑ Somatório
Ø Diâmetro

4. 4
1. PARAFUSO
O que é: O parafuso é um elemento de ligação
formada por um corpo cilíndrico, sendo cabeça (há
parafusos sem) e rosca (há alguns com parte da
haste sem rosca).
Emprego: É empregado para fixação de peças
variadas, de forma não permanente e que podem ser
facilmente montadas edesmontadas.
Classificação: Existem quatro grandes grupos de
parafusos
- Passantes, não passantes, de pressão e prisioneiros.
Fabricação: são fabricados por conformação plástica
(prensagem ou rolagem em matrizes abertas) ou por
usinagem (torneamento ou fresamento).
Passante: atravessam as peças e são
fixos com porcas.
Não passante: a fixação da rosca é
feita numa das peças, sem a
necessidade de porca.
Pressão: a pressão é exercida pelas
pontas dos parafusos contra a peça a
ser fixada.
Prisioneiros: são parafusos sem
cabeça roscados em ambas pontas,
para peças que exigem montagem e
desmontagem frequentes.

5. 5
Tipos: Ver tabela abaixo.
Aplicações:
Cabeça sextavada: usado com ou sem rosca, é
aplicado para uniões que necessitam forte aperto (com
chave deboca).
Sextavado interno (Allen): é utilizado em uniões que
necessitam forte aperto em locais com pouco espaço
para manuseio de ferramentas.
Sem cabeça e fenda/sextavado interno: é utilizado para
travar elementos de máquinas não deixando saliências
externas.

6. 6
Cabeça escareada chata com fenda: é usado em
montagens que não sofrem grandes esforços e cuja
cabeça não pode exceder a superfície.
Cabeça redonda com fenda: usado em montagensque
não sofrem grandes esforços, proporcionando bom
acabamento superficial.
Cabeça cilíndrica com fenda: usado na fixação de
elementos nos quais existe a possibilidade de se fazer
um encaixe profundo para a cabeça do parafuso e bom
acabamento superficial.
Cabeça escareada boleada com fenda: usado na
fixação de elementos com pouca espessura ficando a
cabeça embutida.
Rosca soberba (vários tipos de cabeça): usado em
madeira e em peças de alvenaria (junto com buchas
plásticas).
1.1 ROSCAS
O tipo de rosca usada num parafuso irá determinar a sua aplicação.
Veja os tipos na tabela abaixo.
Parafusos e porcas de fixação na
união de peças (ex.: peças e
máquinas em geral).
Fusos que transmitem movimento
suave e uniforme (ex.: máquinas
operatrizes).
Parafusos de grandes diâmetros
sujeitos a grandes esforços (ex.:
equipamentos ferroviários).
Fusos que sofrem grandes
esforços e choques (ex.: prensas
e morsas).
Fusos que exercem grandes
esforços num só sentido (ex.:
macacos de catraca).

7. 7
1.1.1 PASSO DA ROSCA
O passo da rosca é a distância entre dois pontos de um filete ao
correspondente do seu sucessor, ou seja, a cada uma volta do parafuso na
porca, ele se desloca a distância em milímetros correspondente ao passo da
roca. Exemplo: passo 1,25. A cada uma volta do parafuso na porca, ele se
desloca 1,25mm. É definido a partir da aplicação do parafuso. Ele será:
• Grosso ou grande: quando necessitar-se de deslocamento com
velocidade e/ou quando sob esforços muito significativos atuantes
sobre o parafuso;
• Fino ou pequeno: quando necessitar-se de um deslocamento com
precisão, ou seja, baixa velocidade e/ou quando sob esforços
muito baixos atuantes sobre o parafuso.
Os valores de passo para ser 1,5 ou 1,25 entre outros, estão amarrados ao
diâmetro do parafuso, ou seja, são valores tabelados. Feito o cálculo do
diâmetro, procura-se uma tabela e se verifica o passo a ser aplicado ao
parafuso.
1.1.2 ENTRADAS DAS ROSCAS
Existe roscas com mais de uma entrada para os filetes. Há parafusos de
uma, duas e três entradas.
• Uma entrada: o avanço é igual ao passo.
• Duas entradas: o avanço é duas vezes o passo
• Três entradas: o avanço é três vezes o passo.
1.1.3 DIREÇÂO DA ROSCA
As roscas podem ser fabricadas para dar aperto e soltura em dois
sentidos, direita e esquerda. A rosca esquerda, a qual afrouxa-se para o sentido
horário é empregada quando o elemento fixado tem uma alta vibração e gira no

8. 8
sentido contrário ao aperto. Dito isso, opta-se por utilizar uma rosca invertida
para que ao invés de afrouxar, apertar o parafuso ou elemento de fixação.
1.2 DIMENSIONAMENTO DO PARAFUSO
Para dimensionar um parafuso é necessário tomar conhecimento de duas
coisas:
1ª. Saber qual o material dos parafusos a ser usado, e o respectivo coeficiente
de segurança;
2ª. Ter conhecimento das forças (perpendiculares – tração) atuantes no
parafuso.
1.2.1 CÁLCULO SIMPLIFICADO
𝐹𝐶𝑃 =
FPA(N)
NºP
, sendo:
FPC: força que atua em cada parafuso;
FPA: força na placa “a”;
NºP: número de parafusos.

9. 9
2-EXEMPLOS RESOLVIDOS
2.1Exemplo 1:
Calcular o diâmetro dos parafusos que sustentarão as placas. Considerar
material Aço ABNT 1020 LQ e SG=2.
Ra=Rb=1t
Tensão admissível:
𝜎𝑎𝑑𝑚 =
𝜎𝑒
𝑆𝑔
=
210
2
= 105𝑀𝑃𝑎
Placa A:
𝐹𝐶𝑃 =
FPA(N)
NºP
=
10000
2
= 5000𝑁
𝜎𝑎𝑑𝑚 =
𝐹𝐶𝑃(𝑁)
𝐴(𝑚𝑚2)
= 105 =
5000
𝐴
= 𝐴 =
5000
105
= 47,6𝑚𝑚²
Ø = √𝐴(𝑚𝑚2) ∗
4
𝜋
= √
47,6 ∗ 4
𝜋
= 7,7𝑚𝑚

10. 10
Placa B:
𝐹𝐶𝑃 =
FPB(N)
NºP
=
10000
4
= 2500𝑁
𝜎𝑎𝑑𝑚 =
𝐹𝐶𝑃(𝑁)
𝐴(𝑚𝑚2)
= 105 =
2500
𝐴
= 𝐴 =
2500
105
= 23,8𝑚𝑚²
Ø = √𝐴(𝑚𝑚2) ∗
4
𝜋
= √
23,8 ∗ 4
𝜋
= 5,63𝑚𝑚
Comercialmente utilizara-se parafusos M8 porque a diferença de preço
entre os diâmetros calculados é mínima e sendo a favor da segurança e
facilitar a manutenção.
Dá-se a nomenclatura do parafuso por M8, onde:
M: rosca métrica
8: diâmetro externo do parafuso em milímetro
Sendo ela, quando não especificada, rosca triangular de passo x.
2.2 Exemplo 2:

11. 11
Calcular o diâmetro dos parafusos que sustentarão as placas. Considerar
material Aço ABNT 1020 LQ e SG=2.
∑ Fy= 0 RA+RB-4t= 0
∑ Fy= 0 RA+RB= 4t
∑ Ma=0 4.2 – RB.6 =0
∑ Ma=0 8 – RB6= 0
∑Ma=0 RB6= 8
∑Ma=0 RB=
8
6
= 1,33𝑡
∑ Fy= 0 RA+1,33= 4t
∑ Fy= 0 RA=4t – 1,33t
∑ Fy= 0 RA= 2,67t
Tensão admissível:
𝜎𝑎𝑑𝑚 =
𝜎𝑒
𝑆𝑔
=
210
2
= 105𝑀𝑃𝑎
Placa A:
𝐹𝐶𝑃 =
FPA(N)
NºP
=
26700
4
= 6675𝑁
𝜎𝑎𝑑𝑚 =
𝐹𝐶𝑃(𝑁)
𝐴(𝑚𝑚2)
= 105 =
6675
𝐴
= 𝐴 =
6675
105
= 63,57𝑚𝑚²
Ø = √𝐴(𝑚𝑚2) ∗
4
𝜋
= √
63,57 ∗ 4
𝜋
≈ 9𝑚𝑚
Placa B:
𝐹𝐶𝑃 =
FPB(N)
NºP
=
13300
2
= 6650𝑁

12. 12
𝜎𝑎𝑑𝑚 =
𝐹𝐶𝑃(𝑁)
𝐴(𝑚𝑚2)
= 105 =
6650
𝐴
= 𝐴 =
6650
105
= 63,33𝑚𝑚²
Ø = √𝐴(𝑚𝑚2) ∗
4
𝜋
= √
63,33 ∗ 4
𝜋
≈ 9𝑚𝑚
2.3Exemplo 3:
Calcular o diâmetro dos parafusos que sustentarão as placas. Considerar
material Aço ABNT 1020 LQ e SG=2.
∑ Fx= 0 𝑅𝐴𝑥 − 𝑅𝐵𝑥 = 0
∑ Fx= 0 𝑅𝐴𝑥 = 𝑅𝐵𝑥
∑ Fx= 0 𝐶𝑜𝑠30° . 𝑅𝐴 = 𝐶𝑜𝑠60° . 𝑅𝐵
∑ Fx= 0 0,86 . 𝑅𝐴 = 0,5 . 𝑅𝐵
∑ Fx= 0 𝑅𝐴 =
0,5𝑅𝐵
0,86
= 0,58𝑅𝐵
∑ Fy= 0 𝑅𝐴𝑦 + 𝑅𝐵𝑦 − 10𝑡 = 0
∑ Fy= 0 𝑅𝐴𝑦 + 𝑅𝐵𝑦 = 10𝑡
∑ Fy= 0 𝑆𝑒𝑛30°. 𝑅𝐴 + 𝑆𝑒𝑛60°. 𝑅𝐵 = 10𝑡
∑ Fy= 0 0,5. (0,58𝑅𝐵) + 0,86. 𝑅𝐵 = 10𝑡
∑ Fy= 0 0,29𝑅𝐵 + 0,86𝑅𝐵 = 10𝑡
∑ Fy= 0 1,15𝑅𝐵 = 10𝑡
∑ Fy= 0 𝑅𝐵 =
10
1,15
= 8,6t

13. 13
∑ Fy= 0 𝑅𝐴 = 0,58 . 8,6 = 4,9𝑡
𝑅𝐴𝑦(𝐹𝑃𝐴) = 𝑅𝐴 . 𝑆𝑒𝑛30°
𝑅𝐴𝑦(𝐹𝑃𝐴) = 4,9 .0,5 = 2,45𝑡
𝑅𝐵𝑦(𝐹𝑃𝐵) = 𝑅𝐵 . 𝑆𝑒𝑛60°
𝑅𝐵𝑦(𝐹𝑃𝐵) = 8,6 .0,86 = 7,39𝑡
Tensão admissível:
𝜎𝑎𝑑𝑚 =
𝜎𝑒
𝑆𝑔
=
210
2
= 105𝑀𝑃𝑎
Placa A:
𝐹𝐶𝑃 =
FPA(N)
NºP
=
24500
3
= 8166,66𝑁
𝜎𝑎𝑑𝑚 =
𝐹𝐶𝑃(𝑁)
𝐴(𝑚𝑚2)
= 105 =
8166,66
𝐴
= 𝐴 =
8166,66
105
= 77,77𝑚𝑚²
Ø = √𝐴(𝑚𝑚2) ∗
4
𝜋
= √
77,77 ∗ 4
𝜋
≈ 10𝑚𝑚
Placa B:
𝐹𝐶𝑃 =
FPB(N)
NºP
=
73900
4
= 18475𝑁
𝜎𝑎𝑑𝑚 =
𝐹𝐶𝑃(𝑁)
𝐴(𝑚𝑚2)
= 105 =
18475
𝐴
= 𝐴 =
18475
105
= 175,95𝑚𝑚²
Ø = √𝐴(𝑚𝑚2) ∗
4
𝜋
= √
175,95 ∗ 4
𝜋
≈ 15𝑚𝑚

14. 14
2.4Exemplo 4:
Calcular o diâmetro dos parafusos que sustentarão as placas. Considerar
material Aço ABNT 1020 LQ e SG=2.
Representação da força na placa B, fisicamente:
Placa B:
𝐹𝐶𝑃 =
FPB(N)
NºP
=
100000
2
= 50000𝑁
𝜎𝑎𝑑𝑚 =
𝐹𝐶𝑃(𝑁)
𝐴(𝑚𝑚2)
= 105 =
50000
𝐴
= 𝐴 =
50000
105
= 476,19𝑚𝑚²

15. 15
Ø = √𝐴(𝑚𝑚2) ∗
4
𝜋
= √
476,19 ∗ 4
𝜋
≈ 25𝑚𝑚
Representação da força na placa A, fisicamente:
Placa A:
𝐹𝐶𝑃 =
FPA(N)
NºP
=
50000
3
= 16666,66𝑁
𝜎𝑎𝑑𝑚 =
𝐹𝐶𝑃(𝑁)
𝐴(𝑚𝑚2)
= 105 =
16666,66
𝐴
= 𝐴 =
16666,66
105
= 158,73𝑚𝑚²
Ø = √𝐴(𝑚𝑚2) ∗
4
𝜋
= √
158,73 ∗ 4
𝜋
≈ 15𝑚𝑚
3-EXERCICIOS

16. 16

17. 17

18. 18

19. 19

20. 20

21. 21

22. 22
4. REFERÊNCIAS BIBLIOGRÁFICAS
Elementos de Máquinas. Parte II – Características dos Elementos. Eng. Mec.
Norberto Moro e Téc. Em Mec. André Paegle Auras. Santa Catarina: IFSC –
2006
www.sandvik.coromant.com/pt-pt/knowledge/threading/thread-turning/choice-of-
-application/how-to-apply