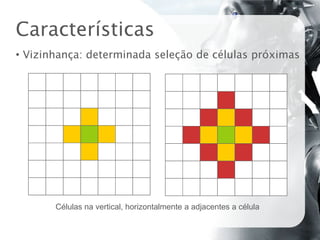
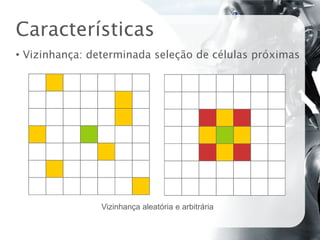
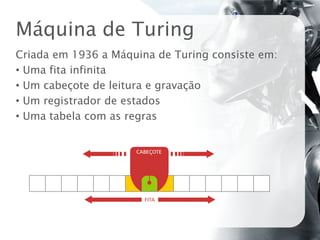
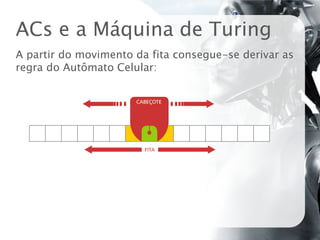
O documento discute autômatos celulares, definindo-os como modelos matemáticos compostos por células em grade que evoluem segundo regras locais. Apresenta contribuições históricas como o Jogo da Vida de Conway e os trabalhos de Wolfram, e exemplos de aplicações como simulação de sistemas físicos, biológicos e musicais.

1. INTELIGÊNCIA ARTIFICIAL: Autômatos Celulares

2. INTELIGÊNCIA ARTIFICIAL: Autômatos Celulares
Marcelo Ramos – Introdução e definição
Sabrina Mariana – Evolução e histórico
Wilson Rodrigues – Aplicações e exemplos

3. Referências
Autômatos Celulares: Revisão Bibliográfica e Exemplos
de Implementações
Lucas Gremonini e Eduardo Vicentini
Revista Eletrônica Lato Sensu – Universidade Estadual do Centro-
Oeste
Autômatos Celulares: Teoria e Aplicações
Flávio Pádua e Professor Newton Vieira
Universidade Federal de Minas Gerais.

4. Autômatos Celulares
• Surgiu nos anos 40 objetivando criar sistemas
evolutivos
• Possui aplicação em diversas áreas:
• Modelagem de sistemas físicos, biológicos e sociológicos
• Aplicativos que processam imagens digitais

5. Definição
Autômatos Celulares são modelos matemáticos
delimitados por uma malha contendo células que são
identificadas por estados. Os estados evoluem através
de regras de interação locais e com evolução temporal.

6. Características Básicas
• Paralelismo
• Localidade
• Homogeneidade

7. Características
A Geometria é a forma da grade de células, formada
por dimensão e formato.
Dimensões:

8. Características
A Geometria é a forma da grade de células, formada
por dimensão e formato.
Formatos da células:

9. Características
• Regras: regras para alteração dos estados das células
• Determinísticas
• Não determinísticas
• Estados: estados em que célula poderá ficar

10. Características
• Vizinhança: determinada seleção de células próximas
Células na vertical, horizontal e diagonalmente adjacentes à célula

11. Características
• Vizinhança: determinada seleção de células próximas
Células na vertical, horizontalmente a adjacentes a célula

12. Características
• Vizinhança: determinada seleção de células próximas
Vizinhança aleatória e arbitrária

13. Autômatos Celulares
Como funcionam na prática?
• Formiga de Langton (vídeo)
• CA-horus Line (animação)
• Sistemas complexos (3D):
• Simulação biológica de micróbios (vídeo)
•Autômato célula 3D (vídeo)

14. Computação Universal
Os Autômatos Celulares apresentam características e
propriedades da computação universal. Prova disso é
que os Autômatos Celulares são capazes de simular
passo a passo a Maquina de Turing.

15. Máquina de Turing
Criada em 1936 a Máquina de Turing consiste em:
• Uma fita infinita
• Um cabeçote de leitura e gravação
• Um registrador de estados
• Uma tabela com as regras

16. ACs e a Máquina de Turing
A partir do movimento da fita consegue-se derivar as
regra do Autômato Celular:

17. John Von Neumann
• Nascido em 28 / Dezembro /1903
• Matemático Húngaro
• Considerado um dos mais importantes matemáticos
do século XX.
• Contribuiu com algumas teorias:
o Teoria dos jogos
o Mecânica quântica
o Ciência da computação
oTeorias Autômato entre outras.

18. Primeiro Autômato Celular
• Objetivo : Simular Sistema Vivo
• Resultado: Primeiro Autômato Celular
o200.000 celular
o Cada celula apresentava
29 estados (cores)

19. John Horton Conway
• Nasceu em Liverpool no final de 1937
• Matemático
•Objetivo: Autômatos Celulares Bidimensionais.
Contribuiu com algumas teorias:
o Invenção do Jogo da vida
o Teoria Combinatória dos jogos
o Nomenclatura para número
excessivamente grandes.

20. Jogo da Vida
• Jogo de zero Jogadores
• Evolução do jogo : determina pelo estado inicial
• As células têm dois estados: estão "vivas" ou
"mortas"
• Uma célula inativa circundada por três células
ativas torna-se ativa
• Uma célula ativa circundada por duas ou três
ativas, permanece ativa;
• Para qualquer outro caso, a célula torna-se
inativa (morre) ou permanece inativa;

21. Jogo da Vida
• O nascimento de uma célula é o agrupamento de
células ativas
• Não podem sobreviver em um isolamento
representado por menos do que duas células
vizinhas ativas
• Uma concentração de mais do que três células
vizinhas ativas levara a célula a se tornar inativa.

22. Stephen Wolfram
• Nascido em meados de 1959 - Londres
• Físico britânico, Matemático, Autor e Empresário
• Alguns Reconhecimentos:
o Teórico em física de partículas
o Cosmologia
o Autômatos Celulares
o Álgebra computacional.

23. Autômatos Wolfram
• Objetivo: Demonstrar que um autômato pode exibir
comportamento complexo mesmo com regras
locais , auto – organização.
• Definição: Modelos matemáticos simples de
sistemas naturais.
• Construídos: Em malhas, rede, células idênticas e
discretas.
• Possuem valor sobre o conjunto finito, onde os
valores evoluem de acordo com as células vizinhas.

24. Divisão dos Autômatos
• Os autômatos são divididos em quatro classes
durante a evolução em espaços-temporais:
• Classe I. Ao estado homogêneo
• Classe II. Estado estável e
periódico , todas as células
possuem o mesmo valor.

25. Divisão dos Autômatos
• Classe III. Estado desordenado,
não possui padrão.
• Classe IV. Gerar estrutura
complexas e imprevisível,
com intervalo de tempos grandes.

26. Aplicações - autômatos celulares
Os Autômatos Celulares são aplicados em diversas
áreas, como: Ciência da Computação, Física, Química,
Geografia, Biologia, Ciências Sociais, entre outras.

27. Aplicações - autômatos celulares
É uma importante ferramenta para simular e estudar
sistemas físicos, químicos, biológicos, vida artificial,
computadores universais, teoria de sistemas
dinâmicos, estudos sobre dinâmicas populacionais.
Exemplo de aplicação AC em Sistemas de Informação Geográficas

28. Exemplos de aplicações
Aplicação de AC com padrões de células que servem
para controlar o ciclo e a duração de simulações de
ondas.
A imagem à esquerda mostra a distribuição aleatória das
células na grade; e à direita mostra os padrões gerados pelo
ciclo oscilatório

29. Exemplos de aplicações
Aplicação de AC para combate à incendios florestais
Figura a) mostra a evolução de um foco de incêndio sem vento

30. Exemplos de aplicações
Figura b) mostra a evolução de um foco de incêndio
com vento
(video incêndio)

31. Exemplos de aplicações
Aplicação de AC utilizado na música
A introdução de dois sistemas musicais baseados
em AC usa o plano cartesiano a fim de representar uma tríade
(conjuntos de 3 notas musicais).
No processo de produção musical, o AC é ajustado inicialmente
com uma configuração aleatória. Após uma determinada
interação, quando um autômato torna-se vivo, as coordenadas
da célula são analisadas para gerar os intervalos e compor a
tríade. Gerando uma sucessão rápida de explosões sonoras de
curta duração (video música)