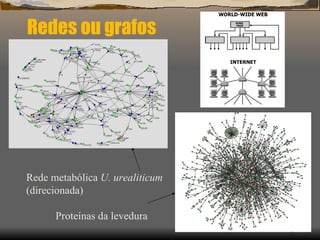
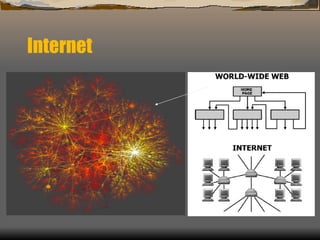
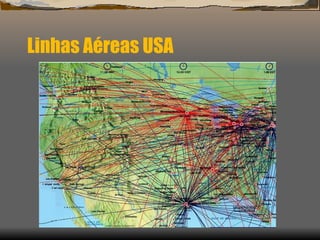
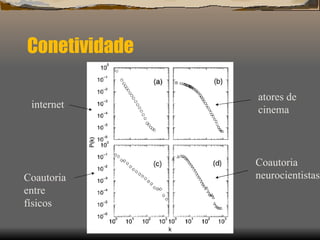
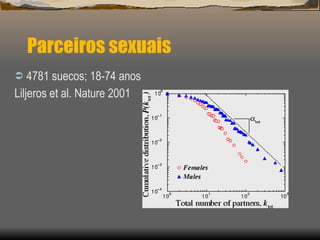
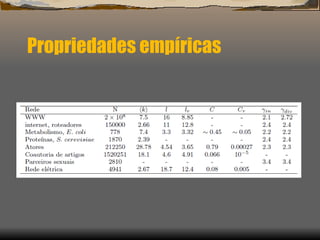
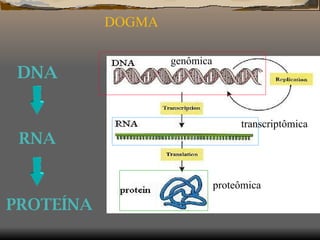
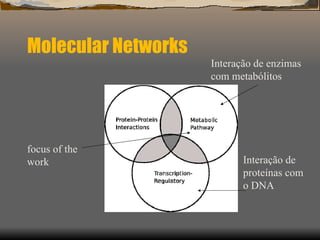
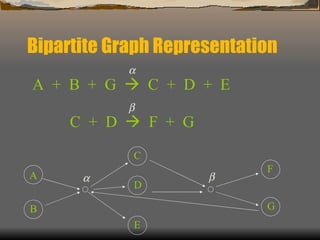
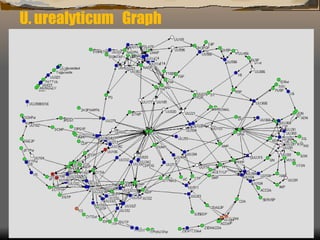
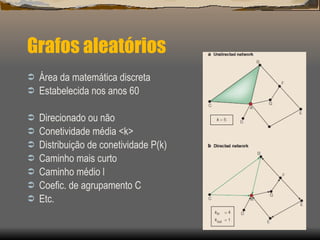
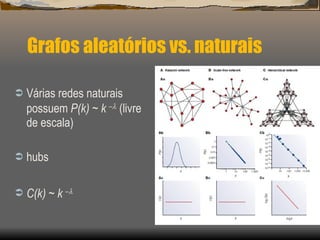
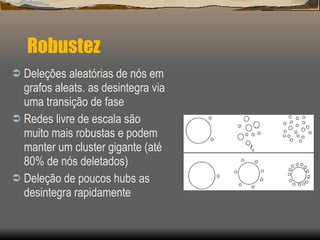
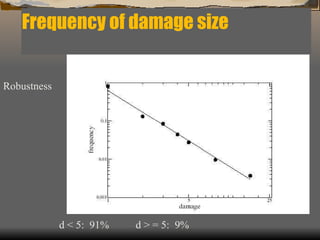
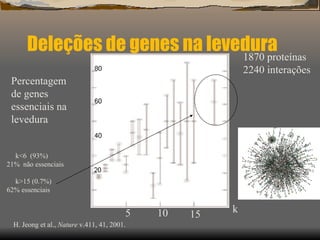
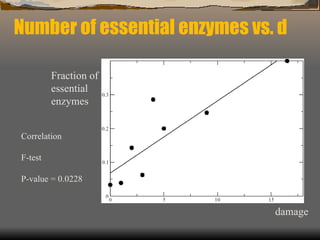
1) O documento discute as propriedades de redes complexas como redes metabólicas, a internet e redes de interação social. 2) Apresenta modelos matemáticos como o modelo de Barabási-Albert para gerar redes livres de escala e discute a robustez dessas redes. 3) Discutem dois estudos: prever a essencialidade de enzimas em redes metabólicas e incluir a atividade gênica em redes moleculares.

1. A Ciência das Redes Complexas II Prof. Dr. José Carlos Merino Mombach Laboratório de Sistemas Complexos Departamento de Física Universidade Federal de Santa Maria (UFSM) Brasil

2. Santa Maria, RS Santa Maria  270.000 habs. UFSM: 20.000 estudantes Foz do Iguacu Porto Alegre Santa Catarina

3. Sumário Introdução Algumas propriedades de grafos aleatórios Propriedades de redes complexas Modularidade Modelos 5.1 Barabási e Albert (construção de redes) 5.2 Lemke et al. (essencialidade de enzimas) Conclusões

4. Introdução O que possuem em comum os seguintes sistemas? O conjunto de reações bioquímicas celulares A WWW (world-wide web) Redes elétricas Redes de interação entre pessoas Resp.: suas topologias são parecidas

5. Redes ou grafos Rede metabólica U. urealiticum (direcionada) Proteínas da levedura

6. Internet

7. Coautoria de artigos co-authorships among 555 scientists cv Lattes

8. Comércio entre empresas

9. Linhas Aéreas USA

10. Rede de doenças humanas

11. Grafos aleatórios Área da matemática discreta Estabelecida nos anos 60 Direcionado ou não Conetividade média <k> Distribuição de conetividade P(k) Caminho mais curto Caminho médio l Coefic. de agrupamento C Etc.

12. Grafos aleatórios Geramos um grafo aleat. com N nós escolhendo pares de nós também aleatoriamente conectando-os com uma dada probabilidade Distribuição de conetividades para N grande Comprimento médio de caminho (´pequeno mundo´) Coeficiente de agrupamento

13. Conetividade internet atores de cinema Coautoria entre físicos Coautoria neurocientistas

14. Parceiros sexuais 4781 suecos; 18-74 anos Liljeros et al. Nature 2001

15. Grafos aleatórios vs. naturais Várias redes naturais possuem P(k) ~ k –   (livre de escala) hubs C(k) ~ k – 

16. Robustez Deleções aleatórias de nós em grafos aleats. as desintegra via uma transição de fase Redes livre de escala são muito mais robustas e podem manter um cluster gigante (até 80% de nós deletados) Deleção de poucos hubs as desintegra rapidamente

17. Deleções de genes na levedura Percentagem de genes essenciais na levedura k 5 10 15 1870 proteínas 2240 interações k<6 (93%) 21% não essenciais k>15 (0.7%) 62% essenciais H. Jeong et al., Nature v.411, 41, 2001.

18. Modularidade Em redes moleculares muitos processos são realizados em módulos Módulos são regiões altamente conectadas da rede Proteínas se associam para realizar tarefas Síntese de proteínas, replicação, reparo do DNA etc. O coefic. C fornece uma medida do nível de modularidade numa rede

19. Propriedades empíricas

20. Referências para leitura Barabási, Reviews of Modern Physics (2002) Barabási, Nature Reviews (2004) Mombach, CNMAC (2004) Livro Edição especial, Science (2009) http://icensa.nd.edu/books.html email: [email_address] Mostrar outros livros

21. Modelos e aplicações Modelo de Barabási e Albert Deleção de enzimas em redes metabólicas Inclusão da atividade dos genes em redes moleculares

22. 1 Modelo de Barabási e Albert Hipóteses básicas do modelo: 1) Crescimento; 2) Conexão preferencial. O algoritmo para construção da rede inicia de um núm. inicial m 0 de nós e a cada passo de tempo um novo nó com m< m 0 arestas é inserido e conectado a outros nós com uma probabilidade proporcional a conetividade dos nós É gerada uma rede livre de escala com expoente ~2,9 (alto!)

23. Modelo de BA Os autores verificaram que as duas hipóteses são necessárias testando modelos que contém apenas uma das hipóteses Sem a conexão preferencial é gerada uma rede com distribuição de conetividades exponencial Sem o crescimento, o modelo inicia de N nós iniciais e evolui para rede com todos os nós conectados

24. Molecular Systems Biology Motivation: Systems biology is the study of an organism, viewed as an integrated and interacting network of genes, proteins and biochemical reactions which give rise to life. (From ISB) Main goal of postgenomics: extract physiology from annotated genome information

25. DOGMA proteômica transcriptômica genômica DNA PROTEÍNA RNA

26. 2 Predicting enzyme essentiality from metabolic networks Motivation:  Can we find a definition of enzyme importance from the metabolic network of an organism?

27. Analysis of E. coli metabolic graph Data from the metabolic network of E. coli was obtained from Palsson´s database http://gcrg.ucsd.edu/personnel/palsson.htm

28. Molecular Networks focus of the work Interação de enzimas com metabólitos Interação de proteínas com o DNA

29. In different files in the KEGG database the same reaction is showed with different directions (reversible or irreversible): Map Pentose Phosphate Pathway R00302 1.1.3.10 D-Glucose + O2  2-Dehydro-D-glucose + H2O2

30. Dealing with inconsistent reaction sets: Excluded reactions: Isolated reactions: reactions may require a metabolite that is not produced by any other reaction or is not available from an external source. External metabolites: Some reactions require metabolites that are not produced inside the cell, however if what is produced is used in other reactions, we determine all external metabolites required and use them as inputs for the simulation.

31. Bipartite Graph Representation A + B + G  C + D + E C + D  F + G   A B   C D E F G

32. Damage ( d ) d = number of metabolites (nodes) deleted from the network metabolites enzyme

33. U. urealyticum Graph

34. Frequency of damage size d < 5: 91% d > = 5: 9% Robustness

35. Sorting enzymes We determine the damage for each enzyme from the simulation Sort the enzymes according to their value of damage Count the number of essential enzymes listed in the PEC database in each class of enzyme damage predicted by our simulation

36. Number of essential enzymes vs. d Fraction of essential enzymes damage Correlation F-test P-value = 0.0228

37. Filtering important genes Two groups: d > = 5: 9% of total  50% of essential enzymes d < 5: 91% of total  50% of essential enzymes

38. Conclusions High damage  metabolites that connect different maps (bridges) Product associated with highest damage in Ecoli  Phosphorybosyl pyrophosphate is the initial substrate of 4 different maps Damage is a good measure of importance for enzymes It can help the indication of potential targets for drugs

39. Conclusões finais A análise por redes complexas está aproximando várias áreas do conhecimento

40. Colaboradores Marialva Sinigaglia (UFRGS) Giovani Librelotto (UFSM) Ney Lemke (UNESP) Rita de Almeida (UFRGS) Gilberto Thomas (UFRGS) Mauro Castro (Cambridge)

41. Referências para leitura Barabási, Reviews of Modern Physics (2002) Barabási, Nature Reviews (2004) Mombach, CNMAC (2004) Livro Edição especial, Science (2009) email: [email_address]