Apresentação joão atividade 3.5
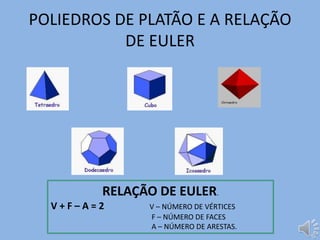
- 1. POLIEDROS DE PLATÃO E A RELAÇÃO DE EULER RELAÇÃO DE EULER. V+F–A=2 V – NÚMERO DE VÉRTICES F – NÚMERO DE FACES A – NÚMERO DE ARESTAS.
- 2. TETRAEDRO V + F - A = 2 VÉRTICE FACE ARESTA 2 4 4 6 2 Voltar
- 3. CUBO OU HEXAEDRO V + F - A = 2 VÉRTICE FACE ARESTA 2 8 6 12 2 VOLTAR
- 4. OCTAEDRO V + F - A = 2 VÉRTICE FACE ARESTA 2 6 8 12 2 VOLTAR
- 5. DODECAEDRO V + F - A = 2 VÉRTICE FACE ARESTA 2 20 12 30 2 VOLTAR
- 6. ICOSAEDRO V + F - A = 2 VÉRTICE FACE ARESTA 2 12 20 30 2 IR
- 7. ESTE TRABALHO FOI CONSTRUIDO PELOS ALUNOS DA 5ª e 6ª SÉRIE DA ESCOLA MARIA PIA, SOB A ORIENTAÇÃO DO PROF. JOÃO FIM