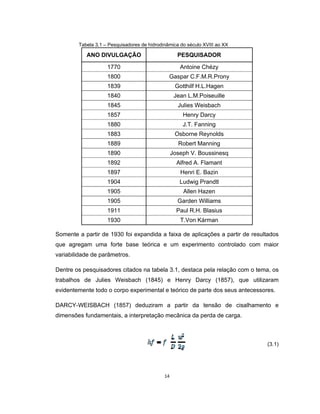
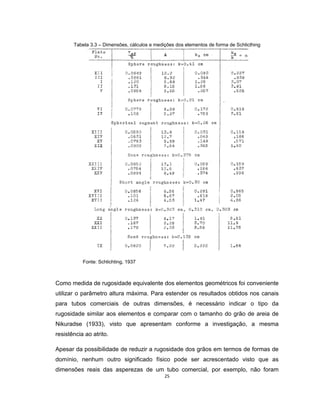
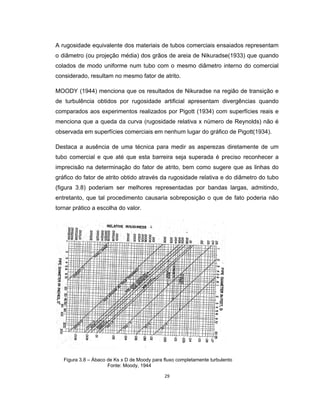
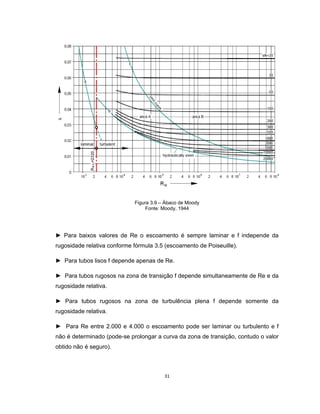
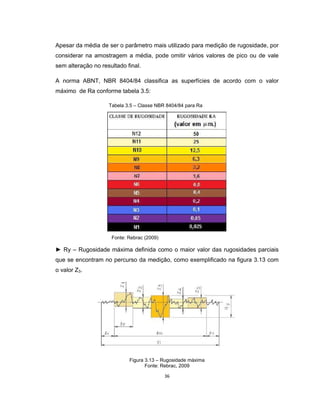
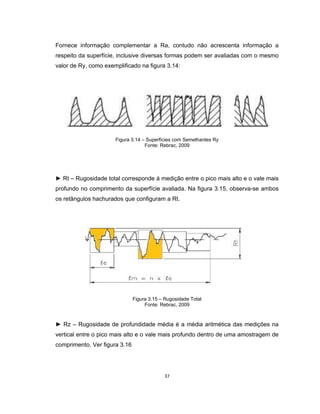
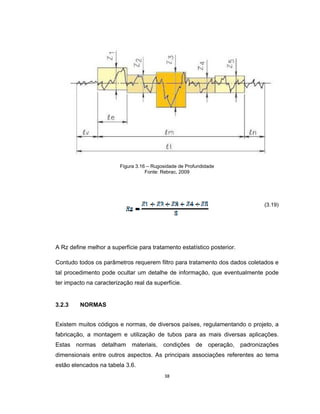
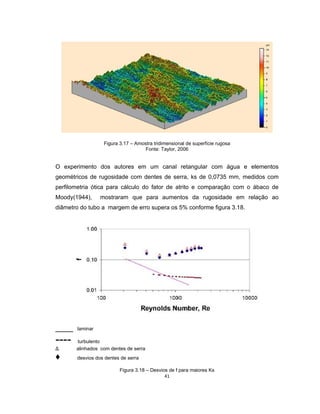
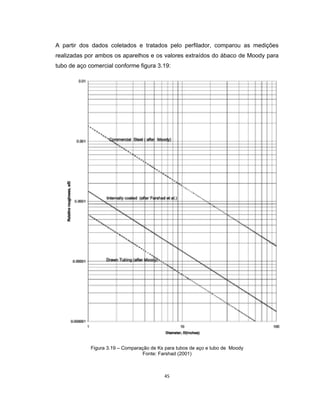
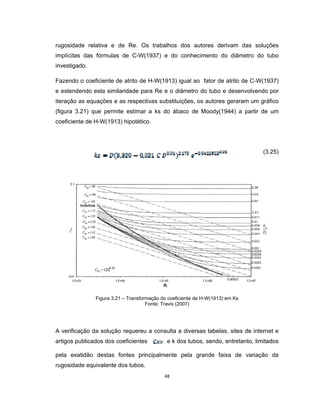
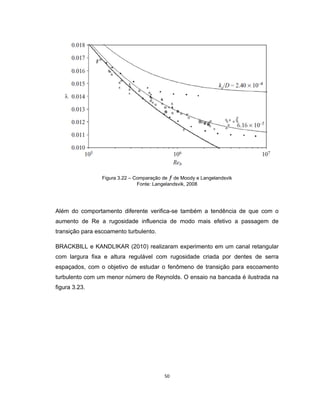
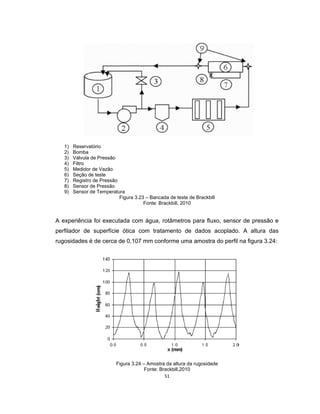
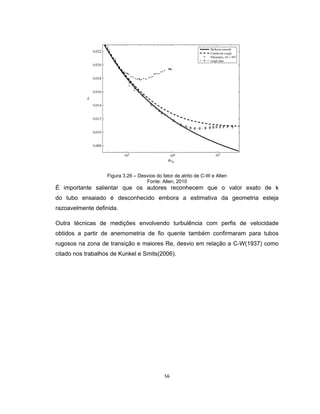
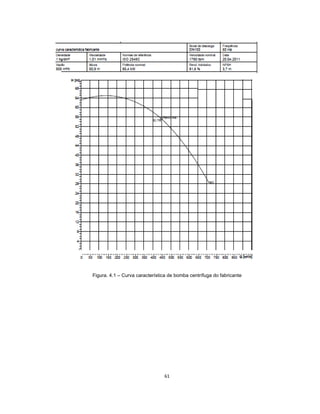
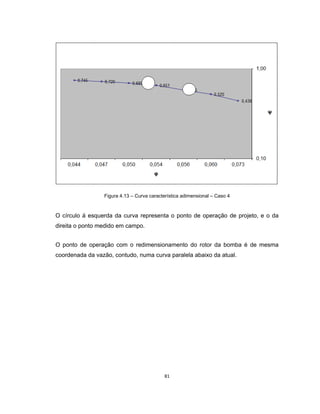
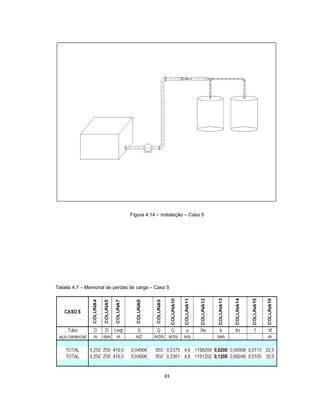
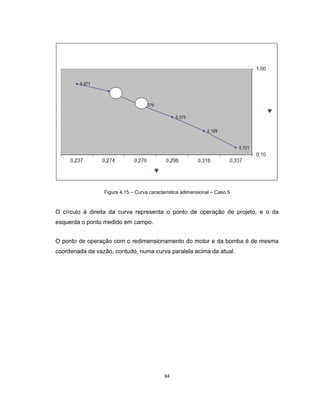
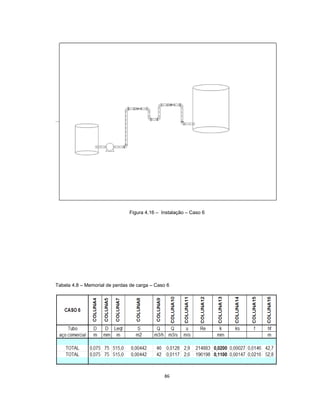
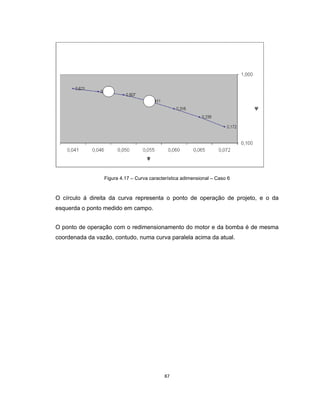
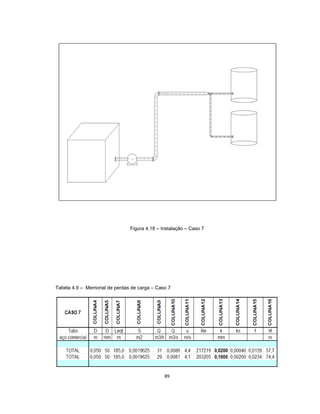
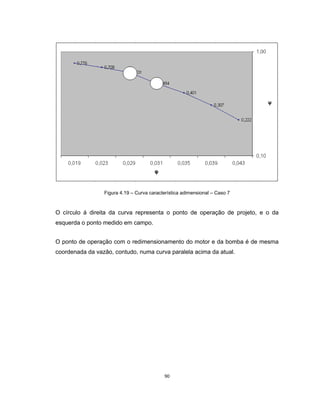
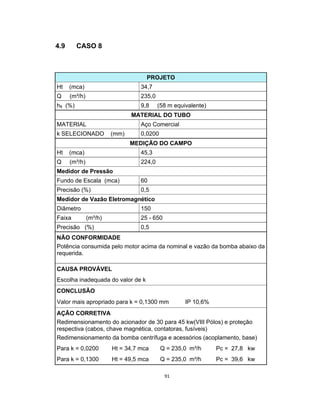
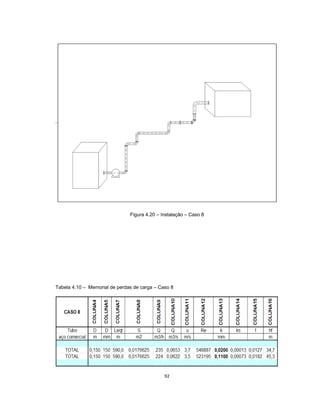
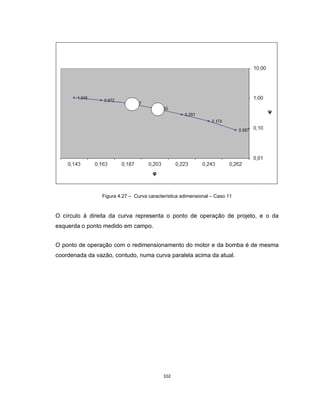
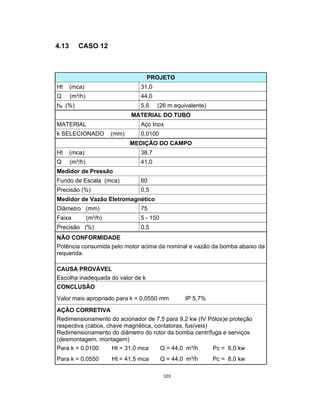
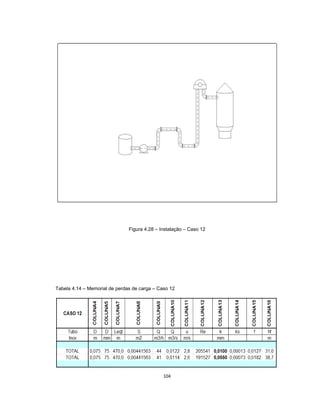
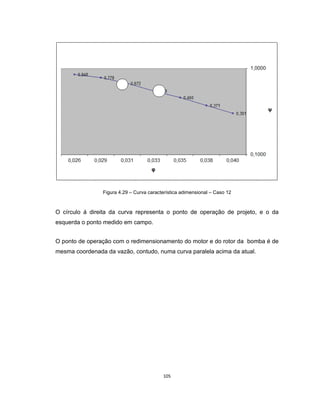
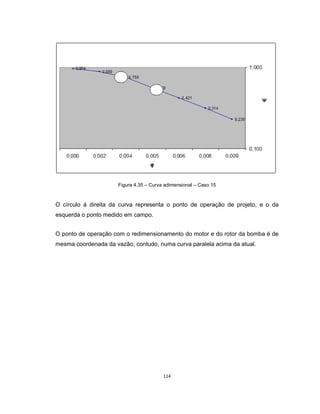
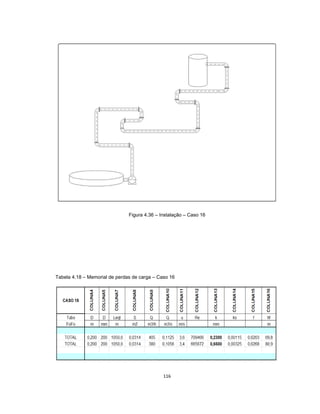
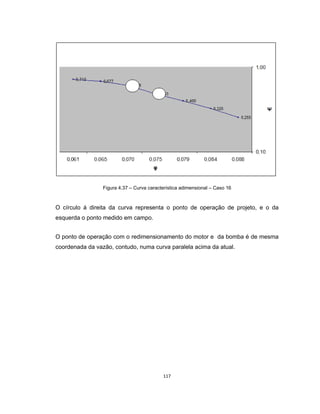
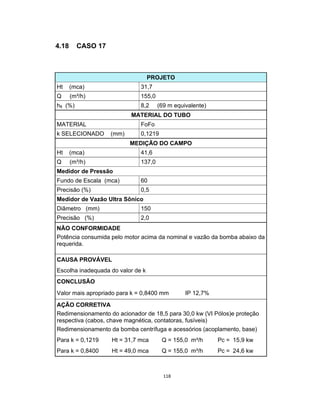
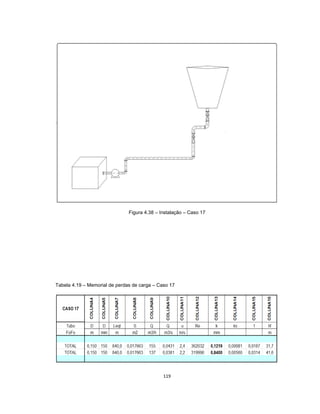
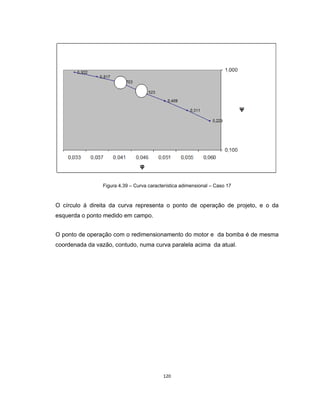
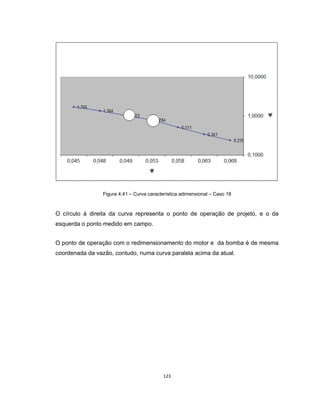
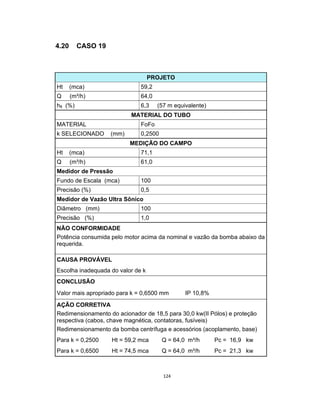
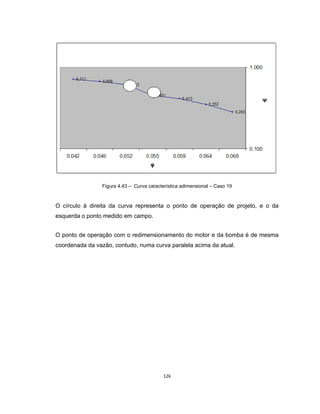
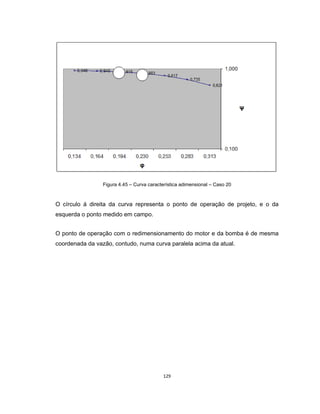
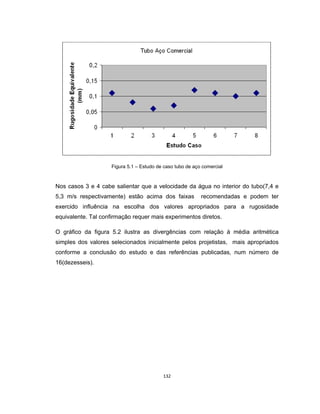
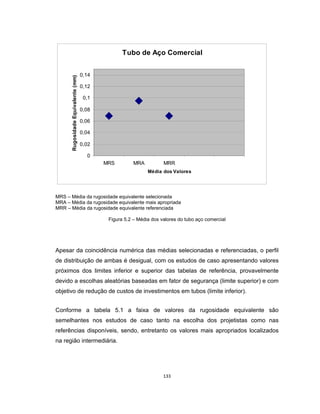
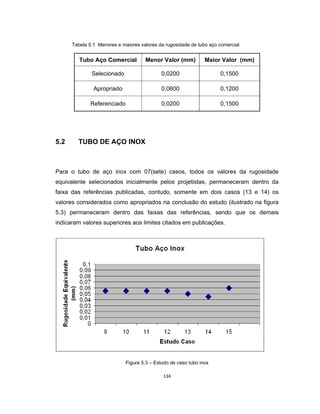
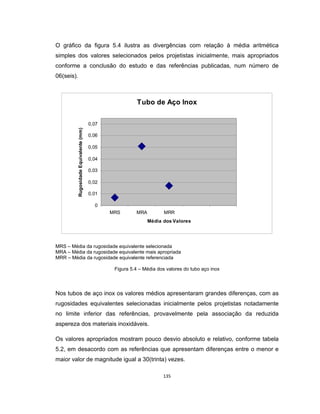
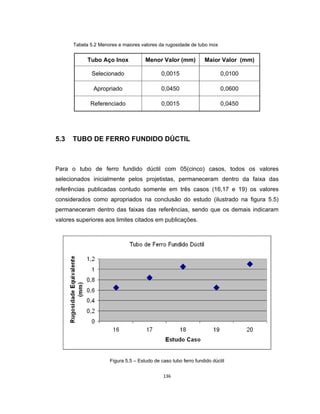
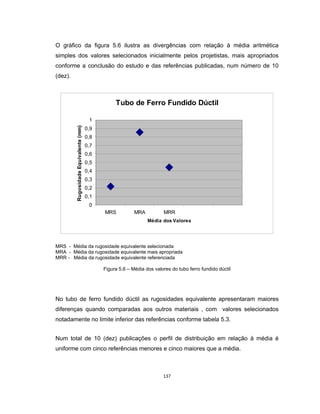
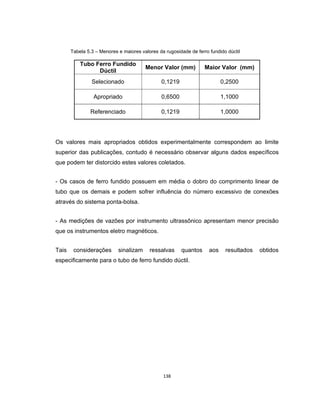
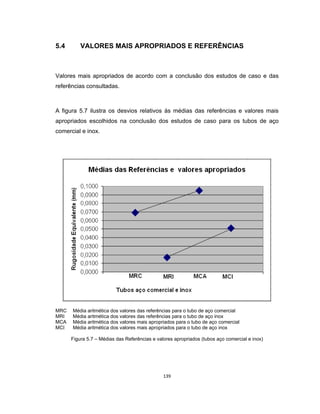
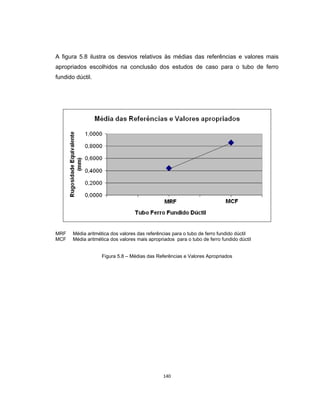
Este documento apresenta uma dissertação de mestrado sobre levantamento da rugosidade equivalente de tubos metálicos. O trabalho pesquisa e esclarece divergências nos valores de rugosidade de tubos comerciais de aço e ferro. Foram realizados testes em 20 sistemas de bombeamento para propor recomendações de estimativa da rugosidade em tubos metálicos rugosos.


![ii
FICHA CATALOGRÁFICA ELABORADA PELA
BIBLIOTECA DA ÁREA DE ENGENHARIA E ARQUITETURA - BAE - UNICAMP
Sch75l
Schroder, Francisco Carlos
Levantamento em campo da rugosidade equivalente
de tubos metálicos / Francisco Carlos Schroder. --
Campinas, SP: [s.n.], 2011.
Orientador: Paulo Vatavuk.
Dissertação de Mestrado - Universidade Estadual de
Campinas, Faculdade de Engenharia Civil, Arquitetura e
Urbanismo.
1. Rugosidade. 2. Fator de atrito. 5. Roughness. I.
Vatavuk, Paulo. II. Universidade Estadual de Campinas.
Faculdade de Engenharia Civil, Arquitetura e
Urbanismo. III. Título.
Título em Inglês: Field survey of the equivalent roughness of mettalic pipes
Palavras-chave em Inglês: Friction factor
Área de concentração: Recursos Hídricos, Enegéticos e Ambientais
Titulação: Mestre em Engenharia Civil
Banca examinadora: Jose Gilberto Dalfre Filho, Rodrigo de Melo Porto
Data da defesa: 24-11-2011
Programa de Pós Graduação: Engenharia Civil](https://image.slidesharecdn.com/schroderfranciscocarlosm-221027144636-6eb0afb4/85/Schroder_FranciscoCarlos_M-pdf-3-320.jpg)