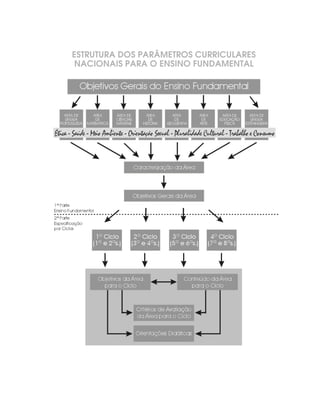
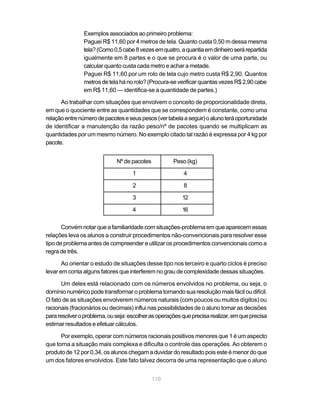
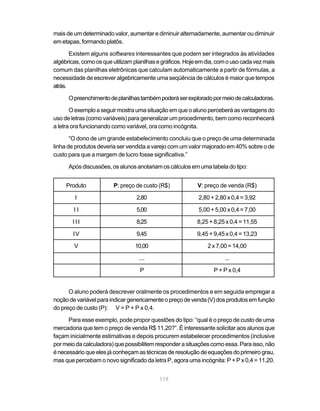
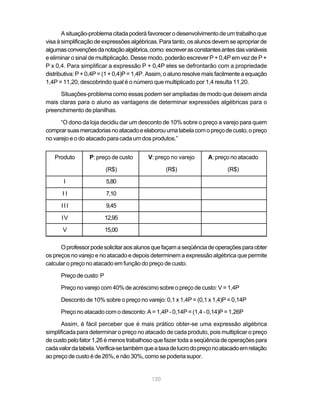
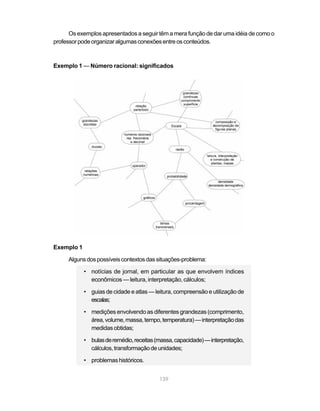
Este documento apresenta os Parâmetros Curriculares Nacionais para o ensino de Matemática nos terceiro e quarto ciclos do ensino fundamental (5a a 8a séries). Ele define objetivos gerais, conteúdos essenciais, e abordagens pedagógicas recomendadas para o ensino da disciplina.