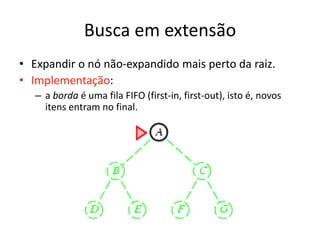
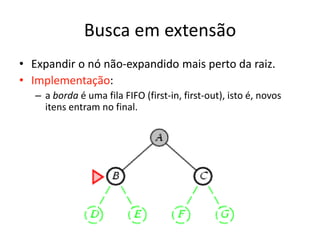
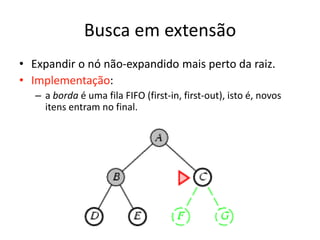
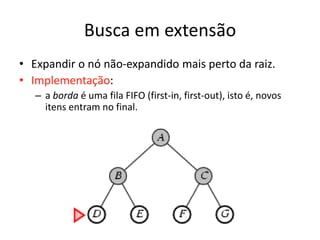
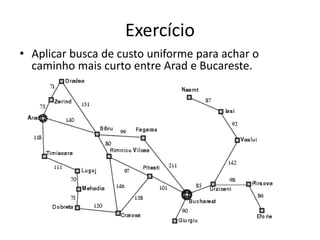
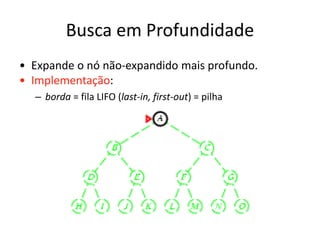
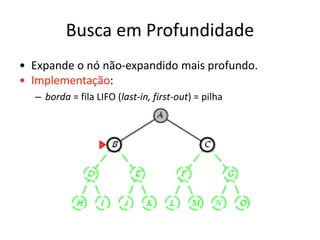
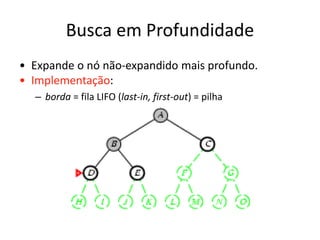
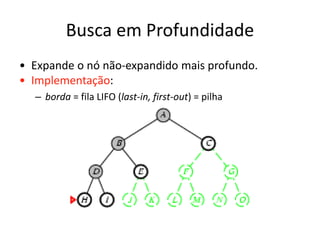
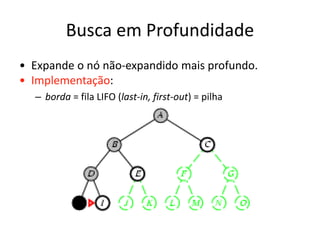
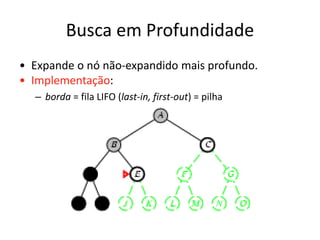
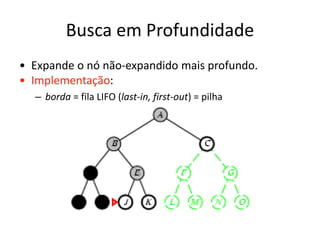
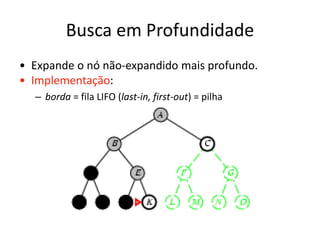
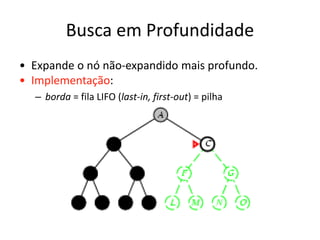
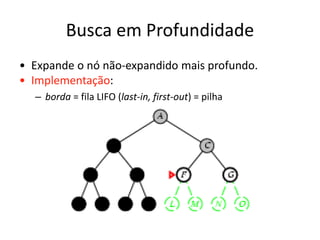
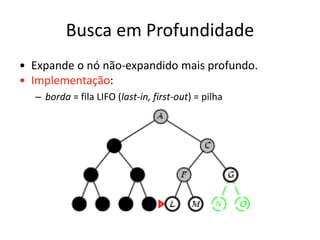
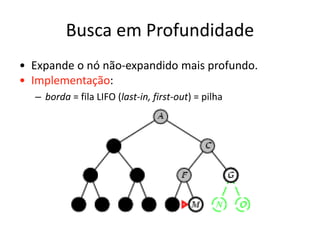
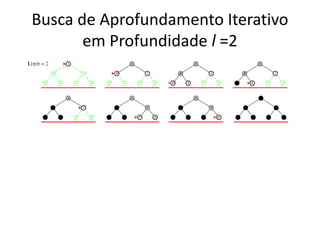
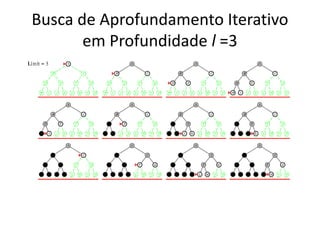
1) O documento discute vários algoritmos de busca para resolução de problemas, incluindo busca em extensão, busca de custo uniforme, busca em profundidade e busca de aprofundamento iterativo.
2) Estes algoritmos são avaliados segundo critérios como completude, complexidade de tempo e espaço e capacidade de encontrar soluções ótimas.
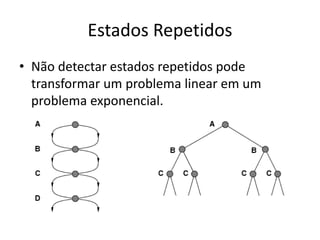
3) A detecção de estados repetidos é importante para evitar loops infinitos e transformar um problema linear em exponencial.