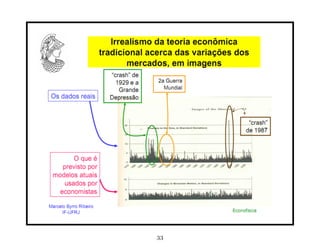
1. O documento discute a interface entre economia e física, conhecida como econofísica. 2. Vários economistas dos séculos 18 e 19 aplicaram métodos e ideias da física em seus estudos econômicos. 3. A teoria dos mercados eficientes assume que os agentes econômicos agem racionalmente para maximizar lucros, levando o mercado a um equilíbrio estável.

1. 1

2. Econofísica: Economia como
um sistema Complexo
Prof. Dr. Rosevaldo de Oliveira
2

3. UFMT
Universidade Federal do Mato Grosso
Departamento de Matem´tica-CUR
a
Econof´
ısica: Economia como
um Sistema Complexo
Prof. Dr. Rosevaldo de Oliveira
Professor: Rosevaldo de Oliveira
3

4. Conte´ do
u
1 O que ´ Econof´
e ısica? 7
2 Per´
ıodo Pr´-Econof´
e ısica 8
3 Teoria Padr˜o: Mercados Eficientes
a 11
3.1 F´
ısica e Economia no final do s´culo 19 . . . . . . . . 11
e
4 S´ries de Pre¸os e Movimento Browniano
e c 14
4.1 Movimento Browniano Geom´trico . . . . . . . . . . . 18
e
5 Instabilidade na Economia Mundial 21
6 Mercado de Op¸˜es
co 22
4

5. 7 O Modelo de Black-Sholes e Merton 24
8 PERIGO 28
9 Distribui¸˜es N˜o-Gaussianas
co a 29
10 Perfei¸˜o versus BOLHAS
ca 30
11 Quebra 34
12 Podemos prever uma Bolha? 37
13 Sistemas Complexos 39
14 Teoria das Cat´trofes
a 40
15 Invariˆncia de Escala e Lei de Potˆncia
a e 43
5

6. 16 Economia Complexa 44
17 Objetivos mais Modestos da Econof´
ısica 47
18 Regula¸˜o dos Mercados
ca 48
19 Econof´
ısica versus Neoliberalismo 50
20 Considera¸˜es Finais
co 52
6

7. 1 O que ´ Econof´
e ısica?
1. A Econof´
ısica ´ a uni˜o da F´
e a ısica com a Economia. Assim
como a Biof´
ısica ´ a uni˜o da F´
e a ısica com a Biologia. E outros
exemplos: F´ısico-qu´
ımica, Geof´
ısica, Astrof´
ısica, ...
2. O termo Econof´ ısica apareceu pela primeira vez em torno de
1994 e foi endossado em um livro de 1999 intitulado
“Introduction to Econophysics” por Mantegna e
Eugene-Stanley.
7

8. 2 Per´
ıodo Pr´-Econof´
e ısica
• Thomas Hobbes (1588-1679) inspirado no trabalho de
Galileu sobre as leis do movimento, em sua obra prima
Leviathan procurou deduzir pela l´gica e a raz˜o como a
o a
humanidade deveria governar-se a si mesma;
• A metodologia ´ a que hoje n´s chamamos de f´
e o ısica te´rica:
o
estipular primeiros princ´
ıpios fundamentais sobre a natureza
humana e de como as pessoas interagem e desenvolvˆ-las at´
e e
onde fosse poss´
ıvel;
• Adam Smith (1723-1790), pai da economia moderna, achou
inspira¸˜o nos “Principia” de Newton ao escrever em 1776 o
ca
seu cl´ssico “Sobre a Riqueza das Na¸˜es” onde usava a id´ias
a co e
de for¸as causais, id´ia completamente nova na ´poca;
c e e
• Adolphe Qu´telet (1796-1874): estudou astronomia e em
e
8

9. 1835 publicou o livro intitulado “Um estudo em f´ ısica
social” onde procurava estabelecer as leis da sociedade
an´logas `s de Newton e m´todos para comparar os dados
a a e
f´
ısicos com os dados sociais (prim´rdios da estat´
o ıstica);
• L´on Walras (1834-1910) e Alfred Marshall (1842-1924)
e
usaram id´ias f´
e ısicas de equil´
ıbrio termodinˆmico para
a
estabelecer os fundamentos da microeconomia onde
desenvolveram a no¸˜o de que um sistema econˆmico atinge o
ca o
estado de equil´ıbrio de forma similar ` teoria dos gases de
a
Maxwell e Boltzmann. A teoria do equil´ ıbrio geral de
Walras, onde a maior parte da teoria econˆmica neocl´ssica
o a
moderna se baseia tem origem nas id´ias vigentes na f´
e ısica da
´poca
e
• Vilfredo Pareto (1848-1923) foi o primeiro economista e
soci´logo a usar modelos matem´ticos junto com evidˆncias
o a e
estat´
ısticas. Descobriu a “lei de Pareto” da distribui¸˜o de
ca
9

10. renda;
• Louis Bachelier (1870-1946) foi orientando de Henri
Poincar´ e em sua tese de doutorado, defendida em 1900 e
e
intitulada “Teoria da Especula¸˜o”, usou id´ias f´
ca e ısicas de
difus˜o e passos aleat´rios (“random walk”) para, 5 anos antes
a o
de Einstein, aplicar m´todos equivalentes ` descri¸ao do
e a c˜
movimento Browniano para explicar a forma¸˜o de pre¸os
ca c
em mercado de a¸˜es. Historicamente foi o primeiro autor a
co
usar matem´tica e f´
a ısica para estudar finan¸as por meio de
c
processos aleat´rios.
o
• Benoit Mandelbrot (1924) foi em 1963 o pioneiro no uso de
distribui¸˜es de cauda longa (n˜o gaussianas) em finan¸as. Foi
co a c
tamb´m quem chamou a aten¸˜o de que a lei de Pareto n˜o
e ca a
passa de uma lei de potˆncia fractal.
e
10

11. 3 Teoria Padr˜o: Mercados Eficientes
a
3.1 F´
ısica e Economia no final do s´culo 19
e
De um lado, os f´ısicos tentavam entender como o movimento dos
´tomos e mol´culas de uma nuvem de g´s produz as
a e a
caracter´ısticas gerais dessa nuvem, como seu volume e sua
temperatura. J´ a economia buscava entender como as
a
decis˜es de cada indiv´
o ıduo de vender ou comprar - o objeto
de estudo da microeconomia - resultam no aumento ou na queda
dos ´
ındices que medem o estado global da economia, como a
infla¸˜o e o PIB, estudados pela macroeconomia.
ca
A ideia ganhou a simpatia daqueles que defendiam um mercado
livre de interven¸˜es ao oferecer a mecˆnica pela qual funcionaria a
co a
“m˜o invis´
a ıvel” de Adam Smith.
Para provar matematicamente a existˆncia de um equil´
e ıbrio
11

12. ´ ´
ESTAVEL E UNICO, os economistas assumem que os agentes
do mercado s˜o todos representados por:
a
• Indiv´
ıduos perfeitamente RACIONAIS
• que agem da maneira mais EFICIENTE poss´ para
ıvel
MAXIMIZAR OS LUCROS.
• No momento em que esses “agentes representativos”
come¸am a negociar, o mercado ruma rapidamente em dire¸˜o
c ca
a um estado de equil´
ıbrio perfeito, em que os pre¸os
c
refletem fielmente o valor real dos produtos.
• A teoria neocl´ssica considera, claro, que na pr´tica o equil´
a a ıbrio
nunca ´ alcan¸ado, uma vez que o mercado n˜o ´ isolado.
e c a e
• Mas entende que not´ ıcias sobre eventos externos ao mercado
chegam ao acaso, atingindo os pre¸os de maneira aleat´ria. Os
c o
pre¸os ent˜o flutuam em torno de seu valor de equil´
c a ıbrio. A
probabilidade dessas flutua¸˜es ´ calcul´vel, e o resultado ´ a
co e a e
12

13. famosa distribui¸˜o gaussiana
ca
13

14. 4 S´ries de Pre¸os e Movimento
e c
Browniano
14

15. 15

16. 16

17. O valor esperado do i-´simo passo ´
e e
E(xi ) = pδ + q(−δ) = (p − q)δ (1)
Ap´s n passos a posi¸˜o ´
o ca e
Xn = x1 + x2 + · · · + xn (2)
E o valor esperado e a variˆncia ´ dado por
a e
E(Xn ) = n(p − q)δ (3)
var(Xn ) = 4pqnδ 2 (4)
A probabilidade de encontrar a part´
ıcula na posi¸˜o x no tempo t ´
ca e
descrita pela equa¸˜o de Kolmogorov ou Fokker-Planck
ca
∂u(x, t) ∂u(x, t) σ 2 ∂ 2 u(x, t)
+µ − =0 (5)
∂t ∂x 2 ∂x2
17

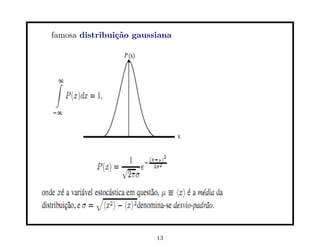
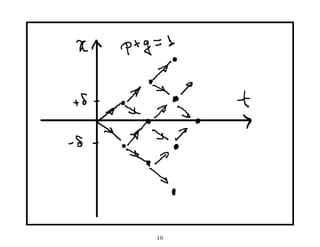
18. A solu¸˜o ´ a distribui¸˜o gaussiana
ca e ca
[ ]
1 (x − µt)2
u(x, t) = √ exp − (6)
2πσ 2t 2σ 2 t
4.1 Movimento Browniano Geom´trico
e
Si sendo o pre¸o de fechamento do ativo ontem, e hoje o pre¸o
c c
Si+1 . O retorno ´ definido por
e
Si+1 − Si
Ri+1 = (7)
Si
quando Ri+1 << 1, ln(1 + Ri+1 ) ≈ Ri+1
Portanto no caso discreto temos
Si+1
Xi+1 ≡ ln( ) (8)
Si
18

19. E no caso cont´
ınuo teremos
S(t)
X(t) ≡ ln( ) (9)
S0
X(t) executa um movimento browniano (µ, σ 2 ).
Podemos rescrever nossos resultados como
dX(t) = µdt + σdW (t) (10)
19

20. 20

21. 5 Instabilidade na Economia Mundial
• Desequil´
ıbrio da economia mundial no in´ dos anos 70
ıcio
• Crise do petr´leo, endividamento, infla¸˜o, varia¸˜es nas taxas
o ca co
de juros e cˆmbio
a
• Colapso do sistema Bretton-Woods para gest˜o da taxa de
a
cˆmbio.
a
• Desregulamenta¸˜o de capitais internacionais especulativos.
ca
• Mercado global 24 horas.
• Como reduzir os RISCOS?
21

22. 6 Mercado de Op¸˜es
co
Conforme Rubash (2001), quando usadas com rela¸˜o aca
instrumentos financeiros, “op¸˜es” s˜o geralmente definidas como
co a
contratos entre duas partes, no qual uma das partes tem direitos
mas n˜o obriga¸˜es em fazer alguma coisa, geralmente a compra ou
a co
venda de algum ativo. Ter direitos mas n˜o obriga¸˜es, tem valor
a co
financeiro, logo os possuidores de op¸˜es devem comprar estes
co
direitos, transformando-os em ativos. Estes ativos derivam seu
valor do valor de outros ativos, da´ chamando-se derivativos. As
ı
op¸˜es de compra (call) s˜o contratos dando ao comprador da
co a
op¸˜o o direito de comprar, enquanto as op¸˜es de venda (put),
ca co
obviamente, d˜o o direito de vender.
a
22

23. 23

24. 7 O Modelo de Black-Sholes e Merton
• 1973 Black-Sholes “The pricing of options and Corporate
Liabilities”. Merton “Theory of Rational of Pricing”.
• Nestes trabalhos eles procuraram estabelecer o chamado
“pre¸o justo” de uma op¸˜o europ´ia obtendo a famosa
c ca e
f´rmula de Black-Sholes.
o
• Prˆmio Nobel de Economia de 1997.
e
O modelo chega a uma equa¸˜o diferencial dada por:
ca
∂c σ 2 S 2 ∂ 2 c ∂c
+ + rS − rc = 0 (11)
∂t 2 ∂S 2 ∂S
Cuja solu¸˜o ´ encontrada abaixo:
ca e
24

25. c = SN (d1 ) − Xe−rT N (d2 ) (12)
p = Xe−rT N (−d2 ) − SN (−d1 ) (13)
(S) ( 2
)
σ
ln X + r+ 2 T
d1 = √ (14)
σ T
(S) ( 2
)
ln X + r − σ
2 T
d2 = √ (15)
σ T
Parˆmetros:
a
• S pre¸o da a¸˜o a vista
c ca
• X pre¸o de exerc´
c ıcio
• r taxa livre de riscos
• T tempo
25

26. • σ volatilidade
• N (x) distribui¸˜o normal
ca
Podemos interpretar N (d1 ) como a probabilidade do pre¸o ` vista
c a
ficar acima do pre¸o de exerc´
c ıcio; e N (d2 ) como a probabilidade do
pre¸o ` vista ficar abaixo do pre¸o de exerc´
c a c ıcio.
26

27. 27

28. 8 PERIGO
• O Risco foi para baixo do tapete!
• O Modelo de Black-Sholes-Merton ´ gaussiano, n˜o leva em
e a
conta eventos mais extremos!
• Um exemplo irˆnico foi a falˆncia do fundo de investimento
o e
Long-Term Capital Management.O fundo faliu ap´s falhar em
o
levar em conta a chance de dois eventos extremos, a bolha
asi´tica de 1997 e a morat´ria da R´ ssia de 1998.
a o u
• O fundo era presidido por Richard Merton e Myron Scholes
28

29. 9 Distribui¸˜es N˜o-Gaussianas
co a
29

30. 10 Perfei¸˜o versus BOLHAS
ca
30

31. • E f´cil entender qualitativamente o que ´ uma bolha no
´ a e
mercado financeiro. Elas acontecem quando os negociantes
acreditam demais na valoriza¸˜o de uma certa mercadoria.
ca
Esse bem pode ser desde uma flor, como as tulipas negociadas
na Holanda em 1636, protagonistas da primeira bolha
financeira da hist´ria, at´ im´veis, caso da bolha
o e o
norte-americana, e outras mais recentes.
31

32. 1 Tulipa=24 Toneladas de Trigo
32

33. 33

34. 11 Quebra
Uma quebra acontece quando um
grande n´ mero de agentes requisita
u
ordens de venda simultaneamente.
Uma quebra acontece quando a ordem ganha (todos tˆm a
e
mesma opini˜o: vendendo), e os tempos normais existem
a
quando a desordem ganha (compradores e vendedores
discordam e se equilibram aproximadamente uns aos outros).
– Um sistema de investidores que s˜o influenciados por seus
a
vizinhos;
– Imita¸˜o local que se propaga espontaneamente na
ca
coopera¸˜o global;
ca
– Coopera¸˜o global entre os investidores que causam uma
ca
quebra;
34

35. – Os pre¸os relacionam-se com as propriedades do sistema;
c
– Os parˆmetros do sistema evoluem lentamente com o tempo;
a
Um modelo com as caracter´ ısticas acima teria as mesmas
“marcas” dos sistemas estudados por Sornette, a saber:
pre¸os seguindo uma lei de potˆncia na vizinhan¸a
c e c
de alguma data cr´ ıtica, com um expoente cr´ ıtico real
ou complexo.
35

36. 36

37. 12 Podemos prever uma Bolha?
– Os economistas nem tentam fazer isso!
´
– E da natureza da economia cl´ssica considerar que crises
a
s˜o inerentes ao setor e n˜o h´ muito a fazer sobre isso, a
a a a
n˜o ser lidar com o problema depois.
a
– Uma das linhas de pesquisa da Econof´ ısica ´ a
e
˜
PREVISAO de BOLHAS.
´
– E o caso de Sornette. Em seu experimento sigiloso iniciado
em 2 de novembro de 2009, ele e sua equipe monitoraram o
sobe-e-desce dos pre¸os de v´rios bens ligados a a¸˜es
c a co
negociadas mundialmente. Eles identificaram nos valores de
quatro deles uma taxa de crescimento que seu modelo
matem´tico identificou como uma bolha. As previs˜es de
a o
Sornette foram guardadas confidencialmente pelo ArXiv,
um servidor on-line p´blico de artigos cient´
u ıficos, e foram
37

38. divulgadas no dia 1o de maio 2010. Quase todas
confirmadas!
– Alan Greenspan, diretor de 1987 a 2006 do Fed (Federal
Reserve, o Banco Central americano), que afirmou ser
poss´ perceber uma bolha somente no momento em que
ıvel
ela explode.Greenspan ficou famoso por dirigir o Fed com
base na chamada teoria neocl´ssica dos mercados
a
eficientes. Prever bolhas seria como prever os n´meros da
u
loteria, e os economistas n˜o poderiam fazer nada para
a
evit´-las.
a
38

39. 13 Sistemas Complexos
– Em um sistema f´ ısico complexo, o TODO n˜o ´ apenas a
a e
soma das PARTES. Por exemplo: a mol´cula de ´gua n˜o
e a a
´ l´
e ıquida, nem gasosa e muito menos s´lida. O estado s´lido,
o o
l´
ıquido ou gasoso ´ o resultado da soma das partes
e
(mol´culas) e n˜o uma propriedade individual.
e a
– O comportamento de um cardume ou um formigueiro
tamb´m est´ baseado nesse mesmo princ´
e a ıpio, como
resultado da intera¸˜o entre os indiv´
ca ıduos EMERGE um
estado coletivo.
39

40. 14 Teoria das Cat´trofes
a
∗ A Teoria da Cat´strofe, iniciada com o trabalho do
a
matem´tico francˆs Ren` Thom na d´cada 60.
a e e e
∗ Em tais sistemas complexos, h´ uma not´vel
a a
propriedade: um padr˜o de comportamento coletivo em
a
larga escala, com uma estrutura intensamente rica. Isto ´ e
resultado de repetidas intera¸˜es n˜o-lineares entre
co a
seus integrantes: tem-se como resultado um tipo de
sinergia - algo maior que a soma individual das partes.
∗ Pequenas mudan¸as em certos parˆmetros de um sistema
c a
n˜o-linear podem fazer com que os equil´
a ıbrios apare¸am
c
ou desapare¸am, ou mudem de atra¸˜o para repuls˜o e
c ca a
vice-versa, conduzindo `s grandes e repentinas mudan¸as
a c
de comportamento do sistema.
∗ A Teoria da Cat´strofe analisa os pontos cr´
a ıticos de
40

41. uma fun¸˜o potencial - pontos onde n˜o apenas a
ca a
primeira derivada, mas uma ou mais derivadas de ordem
mais alta da fun¸˜o potencial tamb´m s˜o zero.
ca e a
∗ H´ sete estruturas gen´ricas para essa geometria das
a e
bifurca¸˜es: Fold, Cusp, Swallowtail, Butterfly,
co
Hyperbolic Umbilic, Elliptic Umbilic e Parabolic Umbilic.
∗ Em geral, comportamentos cooperativos em sistemas
complexos n˜o podem ser reduzidos a uma simples
a
decomposi¸˜o de causas elementares. Deve-se procurar
ca
um ponto de vista mais global, onde a cat´strofe emerge
a
“naturalmente” como uma marca intr´ ınseca fundamental
do fenˆmeno.
o
41

42. 42

43. 15 Invariˆncia de Escala e Lei de
a
Potˆncia
e
A estrutura hier´rquica est´ profundamente ligada a id´ia de
a a e
invariˆncia de escala. Considere a express˜o
a a
1
f (x) = (16)
xα
Tra¸ando o gr´fico desta fun¸˜o, ´ f´cil perceber que podemos
c a ca e a
fazer uma esp´cie de “zoom”: basta realizar a substitui¸˜o
e ca
x → x′ = λx
f (λx) = f (x)λ−α (17)
43

44. 16 Economia Complexa
– A primeira pista dessa complexidade foi observada em 1963
pelo matem´tico polonˆs radicado na Fran¸a Benoit
a e c
Mandelbrot, na ´poca, pesquisador da IBM. Ele estudou
e
uma s´rie hist´rica das flutua¸˜es de pre¸o do algod˜o e
e o co c a
notou que a ocorrˆncia de grandes varia¸˜es era muito
e co
maior que a prevista pela distribui¸˜o gaussiana. A curva
ca
que descrevia a probabilidade de flutua¸˜es dos pre¸os tinha
co c
uma “cauda mais gorda” que a das distribui¸˜es gaussianas
co
(veja figura na p´gina 20).
a
– Nos anos 1990, quando f´ ısicos como Eugene Stanley, da
Universidade de Boston (EUA), e Rosario Mantegna, da
Universidade de Palermo (It´lia), resolveram analisar uma
a
quantidade enorme de dados sobre a¸˜es nas bolsas de
co
valores disponibilizados em formato eletrˆnico. A an´lise de
o a
44

45. v´rias s´ries de pre¸os mostrou que realmente a distribui¸˜o
a e c ca
gaussiana subestimava a ocorrˆncia de grandes flutua¸˜es.
e co
A curva que melhor descrevia as flutua¸˜es nos pre¸os
co c
parecia ser uma “lei de potˆncia”.
e
45

46. 46

47. 17 Objetivos mais Modestos da
Econof´
ısica
“As pessoas arregalam os olhos quando falo em f´ ısica
financeira, e a primeira coisa que me perguntam ´ como fa¸o
e c
para ganhar dinheiro com isso”, conta Rog´rio Rosenfeld,
e
diretor do IFT, que al´m de finan¸as pesquisa cosmologia e
e c
part´ıculas elementares. “Nosso objetivo ´ apenas encontrar o
e
pre¸o justo de um contrato”, explica.
c
47

48. 18 Regula¸˜o dos Mercados
ca
Algumas correntes classificam o per´ıodo em que se gestou a
atual crise como de “financeiriza¸˜o da economia global ”, cujo
ca
in´ teria coincidido com o fim das paridades fixas acordadas
ıcio
em Bretton Woods, em agosto de 1971, decorrente do fim
para paridade d´lar-ouro determinada unilateralmente pelos
o
Estados Unidos.
J´ na d´cada de 1980 economistas cr´
a e ıticos e empres´rios
a
advertiam sobre o risco da financeiriza¸˜o da economia.
ca
Akio Morita, fundador da corpora¸˜o japonesa SONY, assim
ca
refletia os riscos dessa instabilidade:
“Acho que o problema principal est´ em nosso dinheiro. Para
a
manter atividades econˆmicas num sistema livre e aberto, ´
o e
preciso comprar e vender a pre¸os adequados, lembrando que
c
estes pre¸os depender˜o da oferta e da procura. [...] Isso
c a
48

49. porque, acredito, a ind´stria deve ser o fator b´sico no
u a
estabelecimento do valor do dinheiro de um pa´ ıs.”.
49

50. 19 Econof´
ısica versus Neoliberalismo
A economia como sistema complexo sugere que crises s˜o a
sistˆmicas e, portanto, poderiam ser evitadas com a
e
regula¸˜o do sistema - ponto particularmente delicado para
ca
o mundo neoliberal. Como Bouchaud bem lembra, a ideia dos
mercados perfeitos em equil´ ıbrio esteve por tr´s das
a
pol´
ıticas de desregula¸˜o nos ultimos anos nos EUA.
ca ´
“O que precisa ser feito ´ monitorar constantemente o sistema
e
em busca de sinais de instabilidade e vulnerabilidade, disse
Kirman ` Unesp Ciˆncia.”
a e
50

51. 51

52. 20 Considera¸oes Finais
c˜
– Assim como a teoria dos gases ideais ainda ´ v´lida em
e a
partes hoje, a teoria dos mercados eficientes tamb´m possui
e
“verdades parciais”.
– Apelar para os GASES IDEAIS para manter a
DESIGUALDADE SOCIAL e DESTRUICAO DO ¸˜
MEIO AMBIENTE ´ no m´
e ınimo vergonhoso.
– Esperamos que em um futuro “pr´ximo” teremos condi¸˜es
o co
de PREVER COM MAIS SEGURANCA tanto as ¸
cat´strofes FINANCEIRAS OU BOLHAS como
a
TERREMOTOS e outros eventos extremos.
52

53. FIM
53