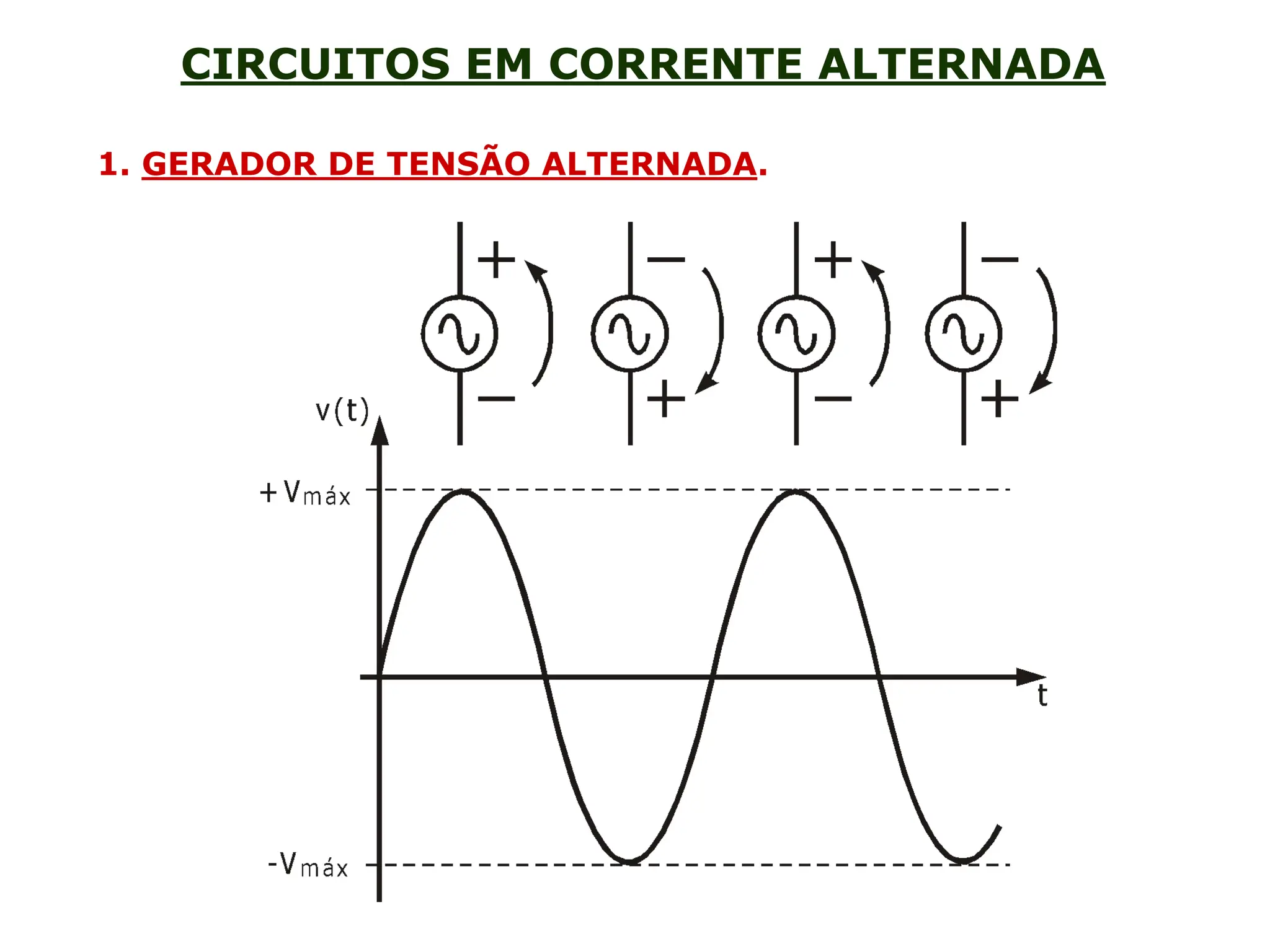
Corrente alternada A corrente alternada (CA) é um tipo de corrente elétrica que se caracteriza por um movimento periódico de vai e vem dos elétrons entre os polos positivo e negativo. A CA funciona através da condução de elétrons que oscilam em volta de um ponto fixo, a uma frequência de 60 Hz. O nome do grupo AC/DC refere-se às iniciais de Alternating Current (corrente alternada) e Direct Current (corrente contínua). 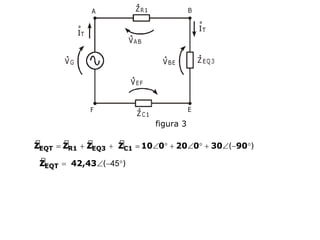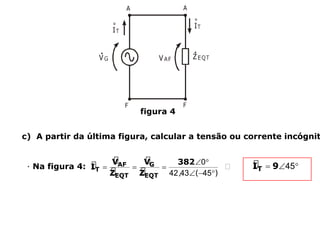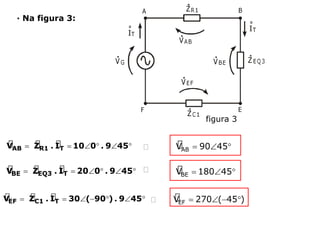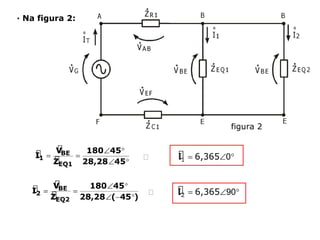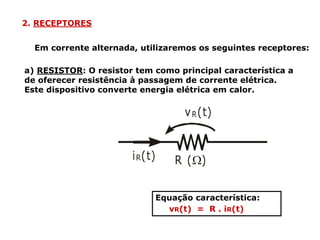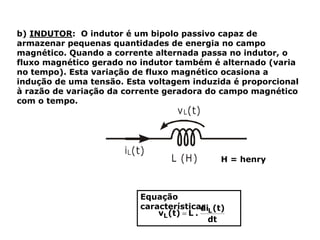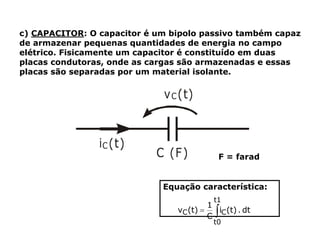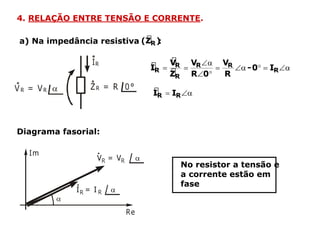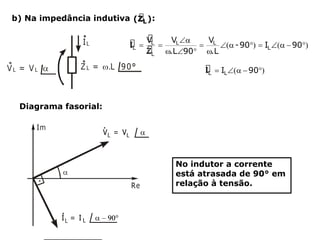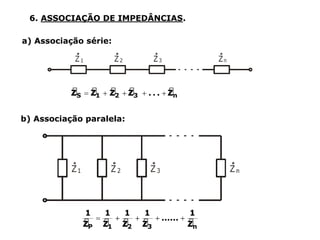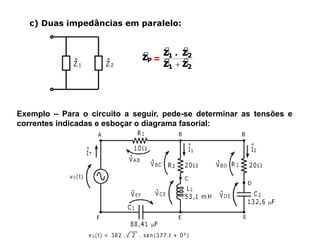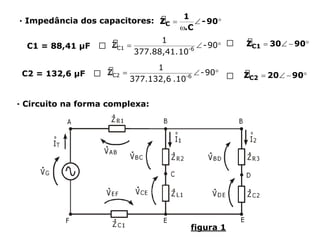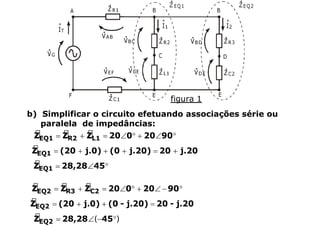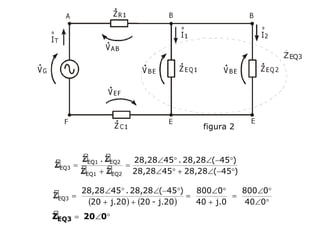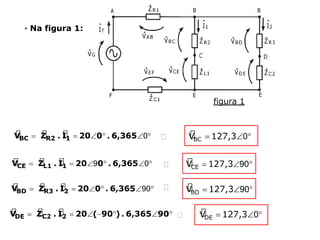Circuitos elétricos Um circuito RLC é um circuito elétrico que contém um resistor (R), um indutor (L) e um capacitor (C).

1. CIRCUITOS EM CORRENTE ALTERNADA
1. GERADOR DE TENSÃO ALTERNADA.

2. v(t) = Vmáx . sen(ω.t + α)
i(t) = Imáx . sen(ω.t +
β)

3. 2. RECEPTORES
Em corrente alternada, utilizaremos os seguintes receptores:
a) RESISTOR: O resistor tem como principal característica a
de oferecer resistência à passagem de corrente elétrica.
Este dispositivo converte energia elétrica em calor.
Equação característica:
vR(t) = R . iR(t)

4. b) INDUTOR: O indutor é um bipolo passivo capaz de
armazenar pequenas quantidades de energia no campo
magnético. Quando a corrente alternada passa no indutor, o
fluxo magnético gerado no indutor também é alternado (varia
no tempo). Esta variação de fluxo magnético ocasiona a
indução de uma tensão. Esta voltagem induzida é proporcional
à razão de variação da corrente geradora do campo magnético
com o tempo.
Equação
característica:
H = henry

5. c) CAPACITOR: O capacitor é um bipolo passivo também capaz
de armazenar pequenas quantidades de energia no campo
elétrico. Fisicamente um capacitor é constituído em duas
placas condutoras, onde as cargas são armazenadas e essas
placas são separadas por um material isolante.
F = farad
Equação característica:

6. 3. IMPEDÂNCIA COMPLEXA
Pode-se demonstrar que as operações matemáticas de integral e
derivada em grandezas que variam harmonicamente no tempo,
com velocidade angular ω, podem ser escritas na forma
complexa (j):
A impedância complexa pode
ser indicada como sendo a
relação entre a tensão
complexa e a corrente
complexa nos receptores:
Lei de Ohm em
corrente alternada:

7. a) Impedância resistiva :
🢡
🢡
b) Impedância indutiva :
🢡
🢡
c) Impedância capacitiva :
🢡
🢡

8. 4. RELAÇÃO ENTRE TENSÃO E CORRENTE.
a) Na impedância resistiva :
Diagrama fasorial:
No resistor a tensão e
a corrente estão em
fase

9. ∙ Gráfico de vR(t) e iR(t):

10. b) Na impedância indutiva :
Diagrama fasorial:
No indutor a corrente
está atrasada de 90° em
relação à tensão.

11. ∙ Gráfico de vL(t) e iL(t):

12. c) Na impedância capacitiva :
Diagrama fasorial:
No capacitor a corrente
está adiantada de 90°
em relação à tensão.

13. ∙ Gráfico de vC(t) e iC(t):

14. 5. RESOLUÇÃO DE CIRCUITOS EM CORRENTE ALTERNADA (CA).
São aplicadas as Leis de Ohm e as Leis de Kirchhoff:
a) Lei de Ohm:
b) 1ª Lei de Kirchhoff: (Lei dos nós ou das correntes):
c) 2ª Lei de Kirchhoff: (Lei das malhas ou das tensões):

15. 6. ASSOCIAÇÃO DE IMPEDÂNCIAS.
a) Associação série:
b) Associação paralela:

16. c) Duas impedâncias em paralelo:
=
Exemplo – Para o circuito a seguir, pede-se determinar as tensões e
correntes indicadas e esboçar o diagrama fasorial:

17. a) Transformar o circuito para forma complexa:
∙ Forma complexa: 🢡
∙ Impedância dos resistores:
R1 = 10Ω 🢡
R2 =R3 = 20Ω 🢡
∙ Impedância do indutor:
L1 = 53,1 mH 🢡
∙ Da expressão vG(t), temos: VG = 382 V
α = 0°
∙ Tensão no gerador:

18. ∙ Impedância dos capacitores:
C1 = 88,41 μF 🢡 🢡
C2 = 132,6 μF 🢡 🢡
∙ Circuito na forma complexa:
figura 1

19. b) Simplificar o circuito efetuando associações série ou
paralela de impedâncias:
figura 1

20. figura 2

21. figura 3

22. figura 4
c) A partir da última figura, calcular a tensão ou corrente incógnit
∙ Na figura 4: 🢡

23. ∙ Na figura 3:
figura 3
🢡
🢡
🢡

24. ∙ Na figura 2:
figura 2
🢡
🢡

25. ∙ Na figura 1:
figura 1
🢡
🢡
🢡
🢡

26. d) Diagrama fasorial: