restrições sobre a relação de preferência: hipóteses de desejabilidade e de convexidade. Apresentação da Função Utilidade: descreve as preferências do consumidor. Quais características as preferências devem ter para poderem ser representadas por uma função utilidade? axiomas

1. Aula anterior
• Definimos o objeto de escolha, o campo de escolha e
também o conjunto factível (ou conjunto orçamentário
walrasiano)
• Definimos a relação de preferência ≥ sobre o conjunto de
consumo X e começamos a discutir as hipóteses que
iremos impor para ≥ de forma a termos um modelo de
escolha
• Relação de preferências é dita ser racional: se é completa e
transitiva
• Outros axiomas:
– ≥ é dita ser contínua se não há mudança bruscas nas
preferências

2. Aula de hoje
• Continuaremos a impor mais restrições sobre
a relação de preferência: hipóteses de
desejabilidade e de convexidade.
• Apresentação da Função Utilidade: descreve
as preferências do consumidor. Quais
características as preferências devem ter para
poderem ser representadas por uma fç
utilidade?

3. Axioma 3: Continuidade
 Definição: A relação de preferência ≥ sobre X é contínua
se ela é preservada nos seus limites. Isto é, para toda
sequência de pares de cestas de consumo {xk , zk}kI tal
que xk ≥ zk (xk ≤ zk)para todo kI e xk  x e zk  z, tem-
se que x ≥ z (x ≤ z).
 Uma forma equivalente da ideia de continuidade é dizer
que para todo x  X= , os conjuntos ≥(x0) e ≤
(x0)
são
fechados em X.
O axioma afirma que não existem súbitas alterações nas
preferências.
A sua razão de ser é puramente matemática.
n
R

5. Desejabilidade
• Ideia: “mais é sempre preferido a menos”
• Para a definição a seguir, assume-se que o
consumo de maiores montantes de bens é
sempre factível, em princípio: isto é, se x  X
e y ≥ x, então, y  X.

6. Axioma 4: Monotonicidade
• Definição 3.B.2 – Mas-colell et all. A relação de
preferência ≥ sobre X é monotônica (monotone) se x
 X e y >> x implica y > x. Ela é fortemente
monotônica (strongly monotone) se y ≥ x e y  x
implica que y > x.
• Jehle e Reny, pag. 10 – Monotonicidade estrita. Para
todo x1
, x2
 X, se x1
≥ x2
então x1
≥ x2
,enquanto que
se x1
>> x2
, então,x1
> x2
.

7. Monotonicidade
• Monotonicidade é satisfeita desde que estejamos
falando de “bens” e não de “males”.
• Se as preferências são monotônicas, você pode ter
indiferença com respeito a um aumento no montante
de alguns bens, mas não de todos os bens.
• Agora, se as preferências são fortemente monotônicas,
se y tem mais de pelo menos um bem e não tem
menos de nenhum, y será estritamente preferida a x.
• Nós temos uma hipótese relativamente mais fraca que
também trata de desejabilidade.

8. Axioma 4’: Não-Saciedade Local
• Def. 3.B.3: A relação de preferência ≥ sobre X é
localmente não-saciada se para todo x  X e
todo e > 0, existe y  X tal que d(x, y) < e e y > x.
Ou seja, na vizinhança de xsempre haverá uma
cesta y que o consumidor prefere.
Note que não-saciedade não requer que a cesta
da vizinhança tenha mais bens... pode ter mais ou
menos... A ideia é só dizer que sempre existe uma
outra cesta preferida.
 
2
1
0
0
0
0
)
(
)
(
)
,
( 






n
i
i
i
T
x
x
x
x
x
x
x
x
d

9. Não-saciedade local
• Se X = , não-saciedade local exclui a
situação extrema onde todos os bens são
‘males’ visto que nesse caso a cesta x=0 seria
um ponto de saciedade local.
n
R

10. Relação entre as duas hipóteses
Exercício 3.B.1. 
• Mostre que:
• a) se ≥ sobre X é fortemente monotônica,
então ela é monotônica.
• b) se ≥ sobre X é monotônica, então ela
respeita não-saciedade local.

11. Implicações sobre a estrutura de preferências
• Não-saciedade local: exclui conjuntos de
indiferença espessos

12. Estas preferências respeitam os axiomas 1 e 2!

14. Implicações sobre a estrutura de preferências
• Monotonicidade: exclui seguimentos com
inclinação positiva da curva de indiferença e
também requer que o conjunto das cestas ≥x0
e ≤x0
estejam, respectivamente, acima e
abaixo de x0
.

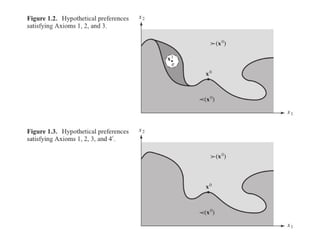
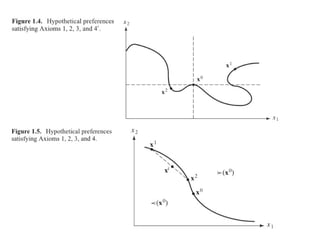
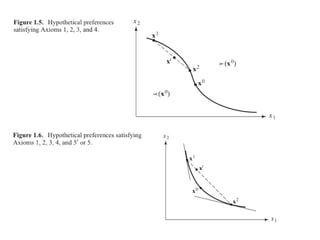
16. Axioma 5’: Convexidade
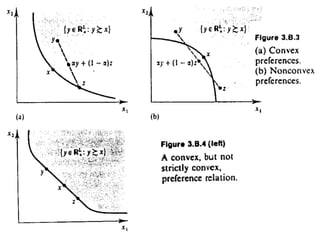
• Def. 3.B.4: A relação de preferência ≥ sobre X
é convexa se para todo x  X, o conjunto
contorno superior {y  X: y ≥ x} é convexo;
isto é, se y ≥ x e z ≥ x, então ty+(1-t)z ≥ xpara
todo t[0,1].
• De outra forma: Para todo (x0
, x1
)  X e para
todo t[0,1], se x1
≥ x0
, então tx1
+(1-t)x0
≥ x0
.
Obs importante = a hipótese de convexidade somente pode ser
assegurada se X (conjunto de consumo) é convexo.

17. Axioma 5: Convexidade Estrita
• Def. 3.B.5: A relação de preferência ≥ sobre X
é estritamente convexa se para todo x  X,
nós temos que y ≥ x, z ≥ x, e y  z então ty+(1-
t)z > xpara todo t(0,1).
• De outra forma: Para qualquer (x0
, x1
)  X e x1
 x0
e para todo t(0,1), se x1
≥ x0
, então
tx1
+(1-t)x0
> x0
.

19. Implicações da convexidade
• O consumidor prefere cestas de consumo
balanceadas (ou diversificadas), ou seja, o
consumidor prefere as médias ponderadas aos
extremos
• Convexidade exclui segmentos côncavos a
origem do conjunto de indiferença;
convexidade estrita exclui segmentos planos
do conjunto de indiferença

20. Implicações da convexidade
• Convexidade pode ser interpretada em termos
de taxas marginais de substituição
decrescentes. Ou seja, de qualquer situação
inicial x, e para qualquer dois bens,
quantidades crescentemente maiores de um
em bem serão necessárias para sucessivas
perdas do outro bem.

21. Implicações da convexidade
• Ou seja, convexidade tem implicações sobre a curvatura dos
conjuntos de indiferença.
• No R2
+ a inclinação do conjunto de indiferença é a TMS do bem 2
pelo bem 1. Convexidade implica que a TMS não pode aumentar
ao longo da curva de indiferença: vc tem que estar disposto a dar
menos de x2 por uma unidade de x1 quando vc tem pouco de x2
relativamente a uma situação onde vc tem muito de x2
– Parêntese: Define-se a taxa marginal de substituição TMS do bem 2
pelo bem 1 como o montante que o consumidor está disposto a
abdicar do bem 2 para obter uma unidade a mais do bem 1, de forma a
permanecer na mesma curva de indiferença.

23. Sobre os axiomas...
• Os axiomas sobre as preferências do consumidor podem ser
descritos da seguinte forma.
– Os axiomas da completude e transitividade estabelecem que
um consumidor pode fazer comparações consistentes entre as
alternativas.
– O axioma da continuidade garante a existência de conjuntos
≥(x0
) e ≤(x0
) bem definidos – seu objetivo é principalmente de
facilitar as ‘contas’.
– Os dois outros axiomas caracterizam propriamente as
preferências do consumidor sobre os objetos de escolha.
Tipicamente, iremos requerer que as preferências mostrem
alguma forma de non-satiation, forte ou fraca, e algum viés a
favor de cestas balanceadas, forte ou fraco.
• Pags 12 e 13

24. Preferências homotéticas e quase-lineares
• Exemplos de preferências para as quais é
possível deduzir as relações completas sobre
todas possibilidades de consumo a partir de
um único conjunto de cestas indiferentes.
• Por essa razão, são bastante utilizadas em
aplicações econômicas, principalmente, em
aplicações econométricas.

25. Definição 3.B.6 – Mas-Collel et all
• Uma relação de preferência ≥ monotônica
sobre X= é homotética se todos os
conjuntos de indiferença são relacionados por
uma expansão proporcional ao longo dos
raios, isto é, se x ~ y então x ~ y , ≥ 0.
n
R

26. Definição 3.B.7 – Mas-Collel et all
• Uma relação de preferência ≥ sobre X= (-, +) x
é quase-linear com relação ao bem 1 (chamado
neste caso de bem numerário) se:
i. Todos os conjuntos de indiferença são
deslocamentos paralelos ao longo do eixo do
bem 1, isto é, x ~ y então (x+e1) ~ (y+e1)
onde e1 = (1, 0, 0, ..., 0) e   R.
ii. O bem 1 é desejável, isto é, (x+e1) > x, x e
>0.
1


n
R

27. Preferências
homotéticas
x
x1
x2
2x
y
2y
x
x1
y
x2
Preferências quase-
lineares

28. Função de utilidade
• Na teoria moderna de microeconomia, a função de
utilidade é apenas uma forma conveniente de
representar a relação de preferência do consumidor.
• Definição 1.5: Uma função ‘u’ avaliada nos reais
é uma função de utilidade representando a relação
de preferência ≥ sobre X= se, para quaisquer x1
e
x2
em X, tem-se:
x1
≥ x2
 u(x1
) ≥ u(x2
).
R
R
u n


:
n
R
Ou seja, se a função de utilidade representa as preferências, ela
deve designar números iguais para cestas indiferentes e
números mais altos para as cestas preferidas...

29. Função de utilidade
• Função utilidade  é interpretada de forma
exclusivamente ordinal
• As curvas de nível da função são denominadas
de curvas de indiferença, pois são idênticas ao
conjunto ~(x0
)
• Ao longo da CI: 0
0 2
2
1
1







 dx
x
U
dx
x
U
dU
2
1
1
2
:
do
Rearranjan
UMg
UMg
dx
dx
TMS 



30. Pergunta
• Quando uma relação de preferência poderá
ser representada por uma função utilidade?

31. Proposição 1.B.2 – Mas-Colell et al.
Proposição: se a relação de preferência ≥ pode ser
representada por uma função utilidade u: X --> R então
ela é racional.
Prova: mostraremos que se u(x) representa uma relação
de preferência ≥ , então, ≥ deve ser racional.
Completude: como u(.) é uma função definida sobre X e
avaliada nos reais (X R), então, para qualquer x e y 
X, ou u(x)≥ u(y) ou u(y)≥ u(x). Como u(.) representa uma
relação de preferência, então, x ≥ y ou y ≥ x. Logo, ≥ é
completa.

32. Proposição 1.B.2 – Mas-Colell et al.
Transitividade: Suponha que x ≥ y e y ≥ z. Como
u(.) representa a relação de preferência, então,
u(x)≥ u(y) e u(y)≥ u(z). Como u(.) é avaliada nos
reais, então, u(x)≥ u(z). Como u(.) representa a
relação de preferencia, então, x ≥ z. Logo, ≥ é
transitiva.

33. Função de utilidade
• Mas será que sempre então que ≥ for racional, haverá
uma função de utilidade para representá-la?1
Não...
Racionalidade é condição necessária mas não
suficiente...
• Pode ser mostrado que qualquer relação de preferência
binária ≥ que é completa, transitiva e contínua pode ser
representada por uma função de utilidade contínua
.
• Nós faremos aqui uma demonstração desse teorema
menos geral, assumindo que ≥ também é monotônica.
R
R
u n


:

34. Proposição 3.C.1
• Suponha que a relação de preferência racional
≥ sobre X seja contínua. Então, existe uma
função de utilidade contínua u(x) que
representa ≥.
Esse é um teorema de existência. Se nós construirmos uma
função que é contínua e que representa tais preferências,
estaremos automaticamente mostrando que existe tal função.
Para facilitar a demonstração, assumimos que X = e que ≥ é
monotônica.
n
R

35. Prova
• Deixe ≥ ser completa, transitiva, contínua e
monotônica.
• Defina Z como sendo um raio diagonal no
• Seja e = (1, 1, ..., 1)  um vetor de uns.
• Então, eZ para todo escalar não-negativo
 >=0
n
R
n
R

36. 1
1
e
x
(x)e
x1
x2
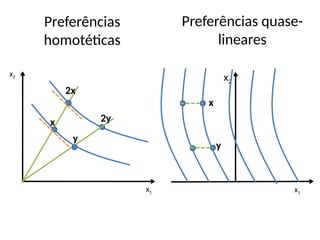
Tomemos uma cesta x
qualquer; notem que por
monotonicidade x ≥ 0; notem
também que para qualquer
a tal que ae >> x, por
monotonicidade , ae ≥ x.
Monotonicidade e
continuidade são então
utilizados para mostrar que
existe um único (x)  [0,
a] tal que (x) e  x.
Z
ae

37. Prova
Perguntas:
i) Será que sempre existirá um escalar (x) tal
que a condição acima seja satisfeita?
ii) Será tal escalar unicamente determinado, tal
que (x) seja uma função bem definida?
iii) Será que ele representará as preferências?

38. Prova
• Existe?
Por continuidade da relação de preferência, os conjuntos
contornos superior e inferior de x são fechados. Então,
os conjuntos
A  { ≥ 0 | e ≥ x}
B  { ≥ 0 | e ≤ x}
são não-vazios e fechados.
Note que se *  A  B, então, *e ~ x tal que (x) =
*. Assim, teremos uma resposta positiva para a 1ª
pergunta acima se mostrarmos que A  B  .
Continuidade da relação de preferência
implica que A e B são fechados em R+
Exercício! 

39. Prova
• Por monotonicidade, 1  A implica ’ A,
para todo ’ ≥ 1 . Assim, A é um intervalo
fechado da forma: [1, )
• Similarmente, por monotonicidade + o fato de
B ser fechado em R+, implica que B é um
intervalo fechado da forma: [0,2]

40. Prova
• Pela completude de ≥, para qualquer  ≥ 0
temos que e ≥ x ou e ≤ x, isto é,  
AB.
• Mas então:
• R+ = BA = [0, 2]  [1, ) – assim, 1 ≤
2. Portanto, A  B  .

41. Prova
É único?
• Suponha que não. Suponha que existam dois
1 e 2 tal que ie ~ x.
• Então, se 1e ~ x e 2e ~ x pela
transitividade de ~ temos que 1e ~ 2e .
Monotonicidade implica que 1 = 2.

42. Prova
• Nós concluímos então que existe no máximo
um escalar, tal que e  x. Esse escalar é (x)
que nós designaremos como nossa função
utilidade u(x).
• Construída tal função de utilidade que designa
um número para cada cesta x, temos que
mostrar que esta função descreve as
preferências ≥ .
• Ou seja, se u(x1
) ≥ u(x2
)  x1
≥ x2

43. Prova
• Considere duas cestas x1
e x2
e os números de
utilidade associados a cada uma delas u(x1
) e
u(x2
), que por definição satisfazem u(x1
)e ~ x1
e u(x2
)e ~ x2
. Então, nós temos que:
x1
≥ x2
P1
u(x1
)e ~ x1
≥ x2
~ u(x2
)e P2
 u(x1
)e ≥ u(x2
)e P3
 u(x1
) ≥ u(x2
) P4
P1  P4  era o que queríamos mostrar.
Monotonicidade de ≥
Exercício: fazer a volta! 

44. Prova
• Resta ainda mostrar que a função que
representa ≥ é contínua.
R
R
u n


:

45. Função de utilidade é única?
• Se u representa uma relação de preferências
então, v = u + 5 também representa!
Função de utilidade é invariante a transformações
monotônicas positivas.
Teorema: Se f: R  R é uma
função estritamente crescente e u: X  R é uma
função utilidade que representa a relação de
preferência ≥ , então a função v: X  R definida por
v(x) = f(u(x)) é também uma função de utilidade
representando a relação de preferência ≥.
n
R
X 


46. Prova
• Sejam x1
 X e x2
 X. Considere a representação
u: X R da relação de preferência ≥ sobre X.
• Então:
• x1
≥ x2
 u(x1
) ≥ u(x2
) [definição da fç utilidade]
• Uma função f: R  R é estritamente crescente:
• u(x1
) ≥ u(x2
)  f(u(x1
)) ≥ f(u(x2
))
• Combinando as duas afirmações temos que:
• x1
≥ x2
 v(x1
) = f(u(x1
)) ≥ f(u(x2
)) = v(x2
).

47. Representações equivalentes de uma mesma
ordenação de preferências
Cesta de
consumo
Ordenação
de
preferências
Função de
utilidade 1
Função de
utilidade 2
Função de
utilidade 3
x0
x0
>x1 3 -1 23
x1
x1
≥x2 2 -2 11
x2
x2
≥x1 2 -2 11
x3
x2
>x3 1 -3 0,5

48. Propriedades cardinais e ordinais
• As propriedades da função utilidade que são
invariantes diante de transformações monotônicas
positivas são chamadas de propriedades ordinais.
• Propriedades cardinais são aquelas não preservadas.
• A relação de preferência associada a função de
utilidade é uma propriedade ordinal.
• Por outro lado, os valores numéricos associados às
cestas de consumo bem como as distâncias entre
elas, são propriedades cardinais.

49. Observações
• De agora em diante, assumiremos que a relação de
preferência ≥ seja contínua e, ptt, representada por alguma
fç de utilidade contínua.
• Notem que a proposição 3.C.1 diz que se a relação de
preferência ≥ for contínua então existe alguma fç de
utilidade contínua que represente tais preferências. Mas,
nem todas as funções de utilidade que representam ≥ são
contínuas.
• Embora transformações monotônicas continuem a
representar as mesmas preferências, não necessariamente
tais transformações preservam a propriedade de
continuidade da função de utilidade.
• Continuidade é uma propriedade ordinal ou cardinal?

50. Observações
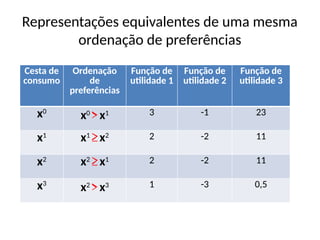
• Muitas vezes iremos requerer que a fç de
utilidade seja (duas vezes) diferenciável ....
• No entanto, nem sempre preferências
contínuas poderão ser representadas por uma
função utilidade diferenciável [preferências de
Leontief]

51. Utilidade marginal e Formato da Função
Utilidade
Implicação do axioma da monotonicidade forte em
termos de utilidade marginal
• Suponha que se dê ao consumidor uma
quantidade adicional do bem i, ou seja, suponha
xi > 0, mantendo todas as quantidades
consumidas dos demais bens constantes. Se vale o
axioma da monotonicidade forte, então:
(x1, x2, ..., xi+xi, ..., xn) > (x1, x2, ..., xi, ..., xn)
ou seja, U > 0.

52. Utilidade marginal e Formato da Função
Utilidade
• Portanto, UMgi = U / xi > 0
• Ou seja, se vale o axioma da monotonicidade
forte, segue que as utilidades marginais são
estritamente positivas.
• O que mais podemos afirmar sobre a forma da
função utilidade???
• Vamos ver mais definições matemáticas antes de
prosseguirmos...

53. Real-valued Functions
A1.4 – pag. 529

54. Definição A1.16: real-valued functions
• f: D  R é uma real-valued function se D é um
conjunto qualquer e R  R
• Ou seja, f uma real-valued function se ela
mapeia os elementos de seu domínio na linha
real.
• Para as definições apresentadas a seguir,
vamos assumir que D é um conjunto convexo.

55. Concavidade da função
• Função côncava: uma função f: D  R é côncava
se, e somente se, para todo x1
, x2
 D tem-se
que f(tx1
+ (1-t)x2
) ≥ t f(x1
) + (1-t) f(x2
) para todo t
 [0,1].
• Função estritamente côncava: uma função f: D 
R é estritamente côncava se, e somente se, para
todo x1
, x2
 D, com x1  x2, tem-se que f(tx1
+ (1-
t)x2
) > t f(x1
) + (1-t) f(x2
) para todo t  (0,1).

56. y
x
f é côncava mas
não é estritamente
côncava
f(tx1
+ (1-t)x2
) = t f(x1
) + (1-t) f(x2
)
x1 x2
xt
f(x1)
f(x2)
f(xt)

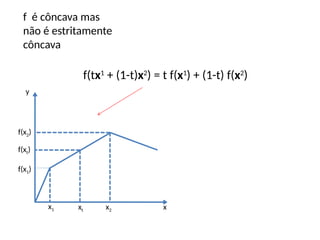
57. Quase-Concavidade da função
• Função quase-côncava: uma função f: D  R é
quase-côncava se, e somente se, para todo x1
, x2

D tem-se que f(tx1
+ (1-t)x2
) ≥ min[f(x1
), f(x2
)] para
todo t  [0,1].
• Função estritamente quase-côncava: uma função f:
D  R é estritamente quase-côncava se, e somente
se, para todo x1
, x2
 D, com x1  x2, tem-se que
f(tx1
+ (1-t)x2
) > min[f(x1
),f(x2
)] para todo t  (0,1).

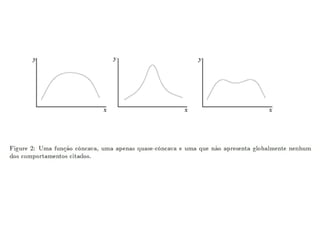
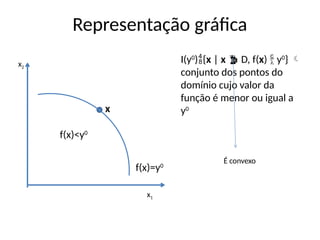
59. Quase concavidade e conjunto contorno
superior
• Existe uma relação também entre a função ser
quase-côncava e o conjunto contorno superior
(pag. 539 – Jehle e Reny)
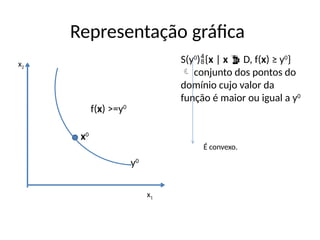
• Defina S(y0
){x | x  D, f(x) ≥ y0
}  conjunto
dos pontos do domínio cujo valor da função é
maior ou igual a y0
• f: D  R é uma função quase-côncava se e
somente se S(y0
) [conjunto contorno superior] é
um conjunto convexo para todo y  R

60. Representação gráfica
x1
x2
f(x) >=y0
x0
y0
S(y0
){x | x  D, f(x) ≥ y0
}
 conjunto dos pontos do
domínio cujo valor da
função é maior ou igual a y0
É convexo.

61. Convexidade da função
• Função convexa: uma função f: D  R é convexa
se, e somente se, para todo x1
, x2
 D tem-se
que f(tx1
+ (1-t)x2
) ≤ t f(x1
) + (1-t) f(x2
) para todo t
 [0,1].
• Função estritamente convexa: uma função f: D 
R é estritamente convexa se, e somente se, para
todo x1
, x2
 D, com x1  x2, tem-se que f(tx1
+ (1-
t)x2
) < t f(x1
) + (1-t) f(x2
) para todo t  (0,1).

62. Convexidade da função
• Função quase-convexa: uma função f: D  R é
quase-convexa se, e somente se, para todo x1
, x2

D tem-se que f(tx1
+ (1-t)x2
) ≤ max[f(x1
), f(x2
)] para
todo t  [0,1].
• Função estritamente quase-convexa: uma função f:
D  R é estritamente quase-convexa se, e somente
se, para todo x1
, x2
 D, com x1  x2, tem-se que
f(tx1
+ (1-t)x2
) < max[f(x1
),f(x2
)] para todo t  (0,1).

63. Quase convexidade e conjunto contorno
inferior
• Existe uma relação também entre a função ser
quase-convexa e o conjunto contorno inferior
(pag. 544 – Jehle e Reny)
• Defina I(y0
){x | x  D, f(x)  y0
}  conjunto
dos pontos do domínio cujo valor da função é
menor ou igual a y0
• f: D  R é uma função quase-convexa se e
somente se I(y0
) é um conjunto convexo para
todo y  R

64. x1
x2
x
Representação gráfica
I(y0
){x | x  D, f(x)  y0
} 
conjunto dos pontos do
domínio cujo valor da
função é menor ou igual a
y0
É convexo
f(x)=y0
f(x)<y0

65. Teorema A1.15
• Uma função côncava é sempre quase-côncava.
Uma função estritamente côncava é sempre
estritamente quase-côncava.
O mesmo se aplica para a função convexa:
• Uma função convexa é sempre quase-convexa.
Uma função estritamente convexa é sempre
estritamente quase-convexa.

66. Mais teoremas...
• A.16: f(x) é uma função (estritamente)
côncava se e somente se –f(x) é uma função
(estritamente) convexa.
• A.19 f(x) é uma função (estritamente) quase-
côncava se e somente se –f(x) é uma função
(estritamente) quase-convexa.

68. restrições sobre ≥ implicam em restrições
na forma das funções utilidade
• Monotonicidade implica em funções utilidade crescente;
• Convexidade das preferências implica que a função de
utilidade é quase-côncava; convexidade estrita implica
quase-concavidade estrita.
• Note que convexidade de ≥ não implica a propriedade
mais forte de que u(.) seja côncava.
• As propriedades de u(.) ser crescente e quase-concava
são propriedades ordinais da fç utilidade, ou seja, são
preservadas diante de transformações monotônicas
positivas.

69. Teorema 1.3 - Propriedades das preferências
e funções utilidade
• Deixe ≥ ser representada por .
Então:
1. u(x) é crescente se e somente se ≥ é
monotônica.
2. u(x) é quase-côncava se e somente se ≥ é
convexa.
3. u(x) é estritamente quase-côncava se e
somente se ≥ é estritamente convexa.
R
R
u n


:
Exercício! 

70. Crescente, estritamente crescente e
fortemente crescente
• Seja f: D  R, onde D é um subconjunto do Rn
.
Então f é crescente se f(x0
) ≥ f(x1
) sempre que
(x0
) ≥ (x1
). Se, em adição, a desigualdade for
estrita sempre que se (x0
) >> (x1
), então, nós
dizemos que f é estritamente crescente. Se, ao
invés f(x0
) > f(x1
) sempre que (x0
) e (x1
) são
distintos e (x0
) ≥ (x1
), então, nós dizemos que f
é fortemente crescente.
Voltar

71. Definição A1.19 – pag 530
• L(y0
) é um conjunto de nível de uma função
avaliada nos reais f: D  R se e somente se
L(y0
) = {x | x  D, f(x) = y0
) onde y0
 R  R.
Voltar

72. Representação gráfica
x1
x2
≥ x0
x0
~ x0
≤ x0
1. ≥ (x0
)  {x | x  X, x ≥
x0
} – conjunto das
cestas pelo menos tão
boas quanto –
conjunto contorno
superior (upper
contour set)
2. ≤ (x0
)  {x | x  X, x0
≥
x} – conjunto das cestas
não melhores do que x0
- conjunto contorno
inferior (lower contour
set)
voltar

73. X (conjunto de consumo) é finito
• Um caso em que sempre é possível
representar uma relação de preferência
racional por uma função utilidade surge
quando X finito.
• Exercício 1.B.5 Mas-Collel et. all pag. 15 
Voltar