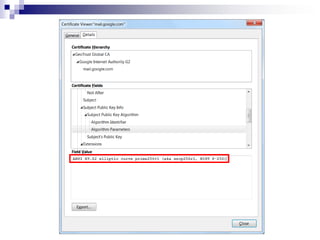
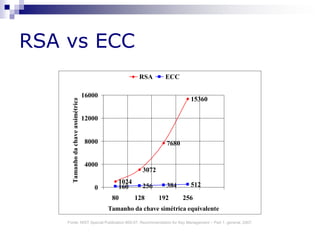
1) O documento discute criptografia baseada em curvas elípticas e seu uso crescente em substituição à criptografia RSA. 2) Apresenta as vantagens do tamanho da chave em curvas elípticas em comparação ao RSA. 3) Levanta questões sobre as curvas elípticas padronizadas pelo NIST e potenciais vulnerabilidades nelas.

1. Cibersegurança e Confiança:
Alguns Aspectos Criptográficos
Paulo S. L. M. Barreto
Professor Associado
Poli/USP

2. Curvas Elípticas
 Grandes provedores de serviços em
nuvem oferecendo acesso “seguro”.
NB: segurança de protocolos do tipo
TLS é um assunto à parte…
 Tendência: substituição de
criptografia RSA por curvas elípticas
(ECC).

4. RSA vs ECC
1024
3072
7680
15360
160 256 384 5120
4000
8000
12000
16000
80 128 192 256
Tamanho da chave simétrica equivalente
Tamanhodachaveassimétrica RSA ECC
Fonte: NIST Special Publication 800-57, Recommendation for Key Management – Part 1: general, 2007.

5. Curvas Elípticas
 QUAIS CURVAS?
 QUAIS ALGORITMOS?

6. Curvas NIST/NSA
 Grande número de normas
internacionais adoptam um conjunto
comum de curvas (NIST FIPS 186,
ANSI X9.62/X9.63, SECG)
 Tecnologia de projeto de curvas data
do final dos anos 1990’s.
 Construídas efetivamente por Jerry
Solinas (funcionário da NSA).

7.  Vulnerabilidade rara (~1 a cada 1012 curvas) ?
Curvas NIST/NSA
 Potencial porta dos fundos conhecida somente
por quem construiu a curva.

8. Sistemas de e-Cash
 Exemplo: Bitcoin.
 Assinaturas digitais ECDSA com a
curva secp256k1: 𝑦2
= 𝑥3
+ 7 sobre
𝔽2256−232−977.
 Segurança ~236
(tempo para quebrar
num PC comum: ~62 s) em vez de
~2128 se um teste crítico for omitido!

9. Sistemas de e-Cash
 Um número muito elevado de vulnerabilidades
deve-se a erros de programação (vide
HeartBleed).

10. Gerador Dual EC
 Geração “segura” de números
aleatórios.
 NSA pagou US$ 107
para pelo menos
uma empresa adotar o gerador Dual
EC como default (fonte: Snowden).
 Depois de 7 anos em uso, NIST
retirou o algoritmo da norma SP
900-90A.

11. Direções?
Curve algorithm security signing verification
Ed25519 EdDSA 𝟐 𝟏𝟐𝟖 𝟔𝟑. 𝟓 𝟐𝟎𝟓. 𝟕
P-224 ECDSA 𝟐 𝟏𝟏𝟐 𝟐𝟔𝟒. 𝟗 𝟓𝟓𝟑. 𝟖
 Esforço corrente do Crypto Forum
Research Group (CRFG) e da IETF para
escolher novas curvas.
 Obstáculos (migração de padrões)!
 Vantagens (tecnologia ~20 anos mais
moderna e robusta que as curvas NIST).
Fonte: eBACS – ECRYPT Benchmarking of Cryptographic Systems; SAC 2015

12. OBRIGADO!

13. APÊNDICE

14. Grupos Elípticos
 Exemplo: conjunto de pontos de uma
curva elíptica 𝑦2
= 𝑥3
+ 𝑎𝑥 + 𝑏.
 Lei de secantes e tangentes.
𝑃
𝑄
𝑃 + 𝑄
−𝑃
𝑂 Fórmulas para calcular
diretamente as
coordenadas do ponto
(𝑥 𝑃, 𝑦 𝑃) + (𝑥 𝑄, 𝑦 𝑄):

15. Problema do Logaritmo
Discreto (Elíptico)
 Dados 𝑃 e 𝑥, é “fácil” calcular 𝑌 = 𝑥𝑃.
 Dados 𝑃 e 𝑌, é “difícil” calcular 𝑥.
 Com valores de 𝑘 bits, ≈ 𝑘3
passos
para calcular 𝑌 (esforço polinomial).
 Para calcular 𝑥, são necessários
≈ 2 𝑘/2
passos computacionais
(esforço exponencial).

16. Gerador Dual EC
 Geração de números aleatórios.
 Escolher pontos “aleatórios” 𝑃 e 𝑄.
 Escolher semente aleatória 𝑟0.
 Para 𝑖 = 1, 2, 3, …:
Calcular 𝑟𝑖 ← 𝑟𝑖−1 𝑃 𝑥, // NB: 𝑁𝑖 = 𝑟𝑖−1 𝑃
Usar 𝑘𝑖 ← 𝑟𝑖 𝑄 𝑥 como 𝑖-ésimo número
aleatório. // NB: 𝐾𝑖 = 𝑟𝑖 𝑄

17. Gerador Dual EC
 O detalhe crítico é que 𝑃 e 𝑄 são
especificados diretamente na norma.
 Exatamente como ocorre em
ElGamal, o conhecimento de 𝑠 tal
que 𝑄 = 𝑠𝑃 permite recuperar mais
informação sobre o sistema.

18. Gerador Dual EC
 Obtendo um único aleatório
𝑘𝑖 = 𝑟𝑖 𝑄 𝑥, a entidade que conhece 𝑠
(aka NSA) pode reconstruir 𝑟𝑖 𝑄 =
𝑟𝑖 𝑠𝑃 = 𝑠 𝑟𝑖 𝑃 = 𝑠𝑁𝑖+1, recuperar
𝑁𝑖+1 = 𝑠−1
(𝑟𝑖 𝑄), e prever todos os
números “aleatórios” posteriores
𝑟𝑖+𝑑 = 𝑁𝑖+𝑑 𝑥, 𝑑 = 1, 2, 3, …