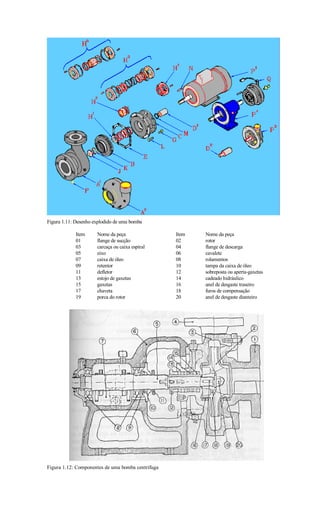
Este documento apresenta os principais conceitos sobre sistemas fluido-mecânicos, com foco em bombas e ventiladores. Descreve a classificação de bombas em volumétricas e turbobombas. Explica o funcionamento de bombas centrífugas, axiais e de fluxo misto. Apresenta também os principais conceitos de escoamento de fluidos, conservação de massa e energia.

1. UNIVERSIDADE METODISTA DE PIRACICABA
CENTRO DE TECNOLOGIA
UNIMEP SANTA BÁRBARA D´OESTE
CENTRO DE TECNOLOGIA
SISTEMAS FLUÍDO-MECÂNICOS
APOSTILA DIDÁTICA
Prof. Antonio Garrido Gallego
Prof. Gilberto Martins

2. Índice
Introdução 1
Capítulo 1: Bombas 2
1.1 Classificação de bombas 2
1.2 Bombas volumétricas ou de deslocamento positivo 2
1.2.1 Bombas de embolo 3
1.2.2 Bombas rotativas 3
1.3 Turbobombas 3
1.3.1 Classificação das turbobombas 4
1.4 Principio de funcionamento de bombas centrifugas ou radiais 5
1.5 Principio de funcionamento de bombas axiais 7
1.6 Principio de funcionamento de bomba diagonal ou fluxo misto 7
1.7 Órgãos constitutivos de uma turbobomba 7
1.7.1 O rotor 7
Referências 10
Capítulo 2: Princípios básicos 11
2.1 Introdução 11
2.2 Escoamento do fluido 11
2.2.1 Fluido 11
2.2.2 Propriedades do fluido 11
2.2.3 Pressão 12
2.2.3.1 Lei de Pascal 12
2.2.3.2 Pressão absoluta e manométrica 13
2.2.3.3 Lei de Stevin 13
2.2.3.4 Carga de Pressão ou altura de coluna de líquido 13
2.2.3.5 Pressão de vapor 13
2.2.4 Escoamento 13
2.2.4.1 Característica da natureza do escoamento 14
2.3 Princípio de conservação 15
2.3.1 Conservação de massa 15
2.3.2 Conservação de energia 16
2.3.2.1 Equação de Bernoulli 16
2.4 Perda de carga 17
2.4.1 Perda de carga ao longo da canalização ou distribuída 17
2.4.1.1 Determinação do coeficiente f 17
2.4.1.2 Perda de carga em canalizações de PVC 19
2.4.1.3 Perda de carga em tubulações de ar 19
2.4.2 Perda de carga localizada 19
2.4.2.1 Método direto 20
2.4.2.2 Método do comprimento equivalente 20
Referências 22
1a lista de exercícios 23
Capítulo 3: Altura manométrica do sistemas 24
3.1 Medição direta da altura manométrica 25
3.2 Altura manométrica de sucção 26
3.3 Altura manométrica de descarga 26
3.4 Curvas características do sistema 26
3.4.1 Levantamento da curva do sistema 26
3.5 Associação de sistemas 29
3.5.1 Associação em série 29
3.5.2 Associação em paralelo 30
3.5.3 Variação da curva característica do sistema 32
3.5.3.1 Variação dos níveis dos reservatórios ou das pressões de 32
aspiração e recalque
3.5.3.2 Variação da perda de carga 32
3.6 Dimensionamento de sistemas de bombeamento 33
3.6.1 Vazão a ser recalcada 33
3.6.2 Diâmetro econômico para uma instalação elevatória 34
3.6.2.1 Fórmula de Bresse 34
3.6.2.2 Fórmula da ABNT 34

3. 3.6.3 Velocidade econômica 35
a
2 lista de exercícios 36
Capítulo 4: Hidráulica de bombas centrífugas 38
4.1 Escolha primária das bombas – gráficos de seleção 38
4.2 Curvas características 39
4.2.1 Curva da altura manométrica x vazão 42
4.2.1.1 Curva tipo estável 42
4.2.1.2 Curva tipo instável 42
4.2.2 Curva da potência consumida x vazão 43
4.2.2.1 Tipo A 43
4.2.2.2 Tipo B 43
4.2.2.3 Tipo C 43
4.2.3 Curva do rendimento x vazão 43
4.2.3.1 Tipo A 44
4.2.3.2 Tipo B 44
4.3 Ponto de operação 45
4.3.1 10 Processo: Variação da curva da bomba 47
4.3.2 20 Processo: Variação da curva do sistema 47
4.3.3 30 Processo: Variação simultânea da curva da bomba e do sistema 47
4.4 Influência do tempo na curva característica da bomba do sistema 47
4.5 Operação próxima ao ponto de vazão nula 48
4.6 Bancada de ensaios de bomba 49
4.6.1 Medição da altura manométrica da bomba 50
4.6.2 Regulagem e medição da vazão 50
4.6.3 Medição da potência necessária ao acionamento 50
4.6.4 Medição do rendimento da bomba 51
4.6.5 Medição da rotação 51
4.6.6 Variação da rotação de acionamento 51
4.7 Leis de similaridade 51
4.7.1 Influência da rotação nas curvas características de uma bomba 52
4.7.2 Influência da variação do diâmetro do rotor nas curvas 52
características de uma bomba
4.7.3 Influência do peso específico nas curvas características de uma 55
bomba
4.8 Velocidade específica 56
Capítulo 5:Associação de bombas 58
5.1 Associação de bombas em série 59
5.2 Associação de bombas em paralelo 59
5.2.1 Associação em paralelo de bombas iguais com curvas estáveis 60
5.2.2 Associação em paralelo de bombas iguais com altura estática 61
variável
5.2.3 Associação em paralelo de bombas diferentes com curvas estáveis 62
5.2.3 Associação em paralelo de bombas iguais com curvas instáveis 63
a
3 lista de exercícios 64
Capítulo 6: Cavitação e NPSH 65
6.1 Pressão de vapor 65
6.2 Altura de colocação de uma bomba 65
6.3 Cavitação 66
6.4 Materiais a serem empregados para resistir à cavitação 68
6.5 Medidas destinadas a dificultar o aparecimento da cavitação 69
6.6 NPSH 70
6.7 Cálculo de referência do NPSH para bombas 71
6.7.1 Conforme KSB 71
6.7.2 Quando se conhece o rendimento máximo 71
a
4 lista de exercícios 72
Capítulo 7: Ventiladores 73
7.1 Princípio de operação 73
7.2 Levantamento das curvas características de um ventilador 74
7.3 Leis de semelhança ou lei dos ventiladores 74
7.4 Tipos de ventiladores e principais características 75
7.5 Curva característica do sistema 75

4. 7.6 Operação de ventiladores em série e em paralelo 78
7.6.1 Associação em série 78
7.6.2 Associação em paralelo 79
Capítulo 8: Sistemas de dutos 81
8.1 Projetos de sistema de dutos 81
8.1.1 O método das velocidades 81
8.1.2 O método de iguais perdas de carga 81
Referências 83
Apêndice
A.1 Propriedades da água 84
A.2 Propriedades do ar 84
A.3 Rugosidade absoluta de diversos materiais 84
A.3a Valores de k – perda de carga em peças especiais 85
A.4 Valores de C para entrada 85
A.5 Valores de C para saídas 86
A.6 Valores de C para cotovelos 88
A.7 Valores de C para expansões 90
A.8 Valores de C para contrações 91
A.9 Valores de C para junções 92
A.10 Valores de C para obstruções 94
A.11 Comprimento equivalente para Ferro e Aço 95
A.12 Comprimento equivalente para PVC 95
B.1 Rugosidade relativa de tubulações 96
B.2 Diagrama de Moody 96
B.3 Perda de carga em canalizações de PVC 97
B.4 Perda de carga em dutos (fluido – ar) 97
C Catálogo de Bombas KSB 98
D Norma Brasileira – 10 126
E Difusor de Ar Circular 144
F Difusor de Ar Retangular 152
G Ventiladores 158

5. Sistemas Fluido-Mecânicos
São equipamentos que tem a função de promover o deslocamento de fluídos, de um ponto a outro de
uma instalação, através da extração/adição de energia de/para um fluido de trabalho.
Os sistemas fluidomecânicos constituem de máquinas de fluido, e sistemas hidráulicos e
pneumáticos.
As máquinas, nesta disciplina, são entendidas como transformadores de energia. São constituídas de um
motor e um gerador, normalmente acoplados através de um eixo. O motor é acionado por uma certa
modalidade de energia, transforma-a em trabalho, que é transmitido, através do eixo, ao gerador. Este, por
seu lado, transforma-o na modalidade final de energia desejada.
Podemos classificar as máquinas hidráulicas em:
1) Máquinas Motrizes: Transformam a energia hidráulica do fluído em trabalho mecânico, principalmente nos
geradores de energia elétrica. Exemplos: Turbinas - Francis - reação, radiais e helicoidal; - Kaplan - reação,
axiais e pás orientadas; - Pelton - ação ou impulsão, de jatos e tangenciais; - Rodas hidráulicas ou roda
d'água;
2) Máquinas Geratrizes: Recebem força motriz (trabalho mecânico) geralmente de máquinas motrizes, para
fornecer energia de pressão e cinética a um fluído. São inúmeros os equipamentos que tem essa função, por
exemplo: compressores de ar, turbo-compressores, ventiladores, bombas, etc.
Como iremos estudar o deslocamento fluídos incompressíveis, trabalharemos na descrição e
selecionamento de Bombas e Ventiladores, além desses equipamentos serem de grande uso em várias ramos
industriais.
Outra classificação das máquinas hidráulicas é:
a) Máquinas de fluido: agente fornecedor ou receptor de energia no rotor é um fluído em escoamento através
das fronteiras do volume de controle; são sub-divididas em máquinas de fluxo e máquinas de deslocamento,
conforme tabela (1.1) e (1.2).
b) Controles hidráulicos e pneumáticos: fluído confinado transmite força, torque ou potência.
Tabela (1.1) Classificação de máquina de Fluido
Máquinas de Fluxo
Fluido de trabalho Designação
líquido turbina hidráulica e bomba centrífuga
gás (neutro) ventilador, turbocompressor
vapor (água, freon, etc) turbina a vapor, turbocompressor frigorífico
gás de combustão turbina a gás, motor de reação
Máquinas de Deslocamento:
Fluido de trabalho Designação
líquido bomba de engrenagens, de cavidade progressiva, de parafuso
gás (neutro) compressor alternativo, compressor rotativo
vapor (freon, amônia, etc) compressor alternativo, compressor rotativo
gás de combustão motor alternativo de pistão
Tabela 1.2: Características Principais
Máquinas de fluxo Máquinas de deslocamento
alta rotação baixas e médias rotações
potência específica elevada (potência/peso) potência específica média p/ baixa (potência/peso)
não há dispositivos com movimento alternativo várias têm dispositivos com movimento alternativo
médias e baixas pressões de trabalho altas e muito altas pressões de trabalho
não operam eficientemente com fluidos de adequadas para operar com fluidos de viscosidade
viscosidade elevada elevada
vazão contínua na maior parte dos casos, vazão intermitente
energia cinética surge no processo de energia cinética não tem papel significativo no
transformação de energia processo de transformação de energia
na maioria dos casos, projeto hidrodinâmico e na maioria dos casos, projeto hidrodinâmico e
características construtivas mais complexas que as características construtivas mais simples que as
máquinas de deslocamento máquinas de fluxo

6. Capítulo 1
Bombas
Bombas são máquinas hidráulicas que transferem energia ao fluído no estado líquido, e que tem a
finalidade de transportá-lo de um ponto a outro através do seu escoamento.
Recebem energia de uma fonte motora qualquer e cedem parte desta energia ao fluído sob forma de
pressão, energia cinética ou ambas, isto é, aumentam a pressão do líquido, a velocidade ou ambas as grandezas.
1.1 Classificação das bombas
Não existe uma terminologia homogênea sobre bombas, pois, há vários critérios para designá-las,
entretanto, poderemos classificá-las em duas grandes categorias:
a) Bombas Volumétricas ou de Deslocamento Positivo;
b) Turbobombas
Tabela 1.3: Classificação de bombas
Bombas centrífugas
passo fixo
1 estágio rotor aberto
de fluxo axial passo variável
multiestágio rotor fechado
rotor aberto
sucção única rotor fechado
de fluxo radial
rotor fechado
(centrífugas)
dupla sucção
1 estágio
de fluxo periférico
multiestágio
Bombas de deslocamento
pistão
alternativas
diafragma
pistão
rotativas lóbulo
engrenagem
parafuso
1.2 Bombas volumétricas ou de deslocamento positivo
Este tipo de bomba tem por característica de funcionamento a transferência direta da
energia mecânica cedida pela fonte motora, em energia potencial(energia de pressão). Esta
transferência é obtida pela movimentação de um órgão mecânico da bomba que obriga o fluído
a executar o mesmo movimento que ele está executando.
O fluído desloca o mesmo volume que realiza o órgão mecânico da bomba, em movimentos alternados.
A variação de órgãos mecânicos (êmbolos, diafragma, engrenagens, parafusos, etc) é responsável pela
variação na classificação das bombas volumétricas ou de deslocamento positivo, as quais podem ser dividas em:

7. a) Bombas de Êmbolo ou Alternativas;
b) Bombas Rotativas;
1.2.1 Bombas de êmbolo
Nas bombas de êmbolo o órgão que produz o movimento do fluído é um tipo de pistão ou diafragma
que, em movimentos alternativos aspira e expulsa o fluído bombeado.
Princípio de funcionamento observando a figura (1.1):
a) Movimento de aspiração com conseqüente fechamento
da válvula de descarga (2) e abertura da válvula de
admissão (1) preenchendo de fluído o volume V1.
b) Movimento de descarga com conseqüente abertura da
válvula de descarga (2) e fechamento da válvula de
admissão (1) esvaziando o fluído do volume V1
imprimindo-lhe uma energia potencial (de pressão).
Observações Gerais:
a) A descarga através da bomba é intermitente;
b) As pressões variam periodicamente em cada ciclo;
c) Esta bomba é capaz de funcionar como bomba de ar,
fazendo vácuo, caso não haja fluído a aspirar.
Figura 1.1: Esquema de uma bomba deslocamento
1.2.2 Bombas rotativas
A denominação genérica, Bomba Rotativa,
designa uma série de bombas volumétricas
comandadas por um movimento rotativo, dando a
origem do nome.
As bombas rotativas podem ser:
a) um só rotor.: palheta, pistão rotativo e parafuso
simples;
b) rotores múltiplos.: parafusos, engrenagens,
parafuso palhetas.
Figura 1.2: Corte de uma bomba de engrenagens
O funcionamento volumétrico de todas elas consiste no preenchimento dos interstícios entre rotor e
carcaça, sendo que a somatória de todos eles, corresponde à vazão total.
1.3 Turbobombas
Este tipo de bomba tem por princípio de funcionamento a transferência de energia mecânica para o
fluído a ser bombeado em forma de energia cinética, por sua vez, esta energia cinética é transformada em energia
potencial (energia de pressão) sendo esta sua principal característica.
Basicamente as turbobombas são constituídas de duas partes fundamentais:
Rotor (impelidor) que é dotado de palhetas responsável pelo movimento do fluido e acionado através de um eixo
que lhe transmite o movimento de rotação
Difusor que é o responsável pela coleta do fluido que sai do rotor e encaminha a tubulação de recalque (saída),
devido a sua forma geometria, este diminuni a velocidade de saída e aumenta a pressão.
1.3.1 Classificação das turbobombas
Em função dos tipos e formas dos rotores, as turbobombas podem ser divididas na seguinte
classificação:
a) Centrífugas Puras ou Radiais (figura 1.3)

8. Quando a direção do fluído bombeado é, em geral, perpendicular ao eixo de rotação.
b) Centrífugas de Fluxo Misto (helicoidal) (figura 1.4)
Quando a direção do fluído bombeado é, em geral, inclinada em relação ao eixo de rotação.
c) Centrífugas de Fluxo Axial (figura 1.5)
Quando a direção do fluído bombeado é paralela em relação ao eixo de rotação.
Figura 1.5: Bomba axial
Figura 1.3: Bomba radial ou
centrífuga Figura 1.4: Bomba de fluxo
periférico ou misto ou helicoidal
Existem diversas outras classificações das bombas centrífugas, não abrangendo necessariamente todos
os tipos.
Dentre tantas consideraremos:
a) Quanto ao número de bocas de sucção do rotor. (figura 1.6)
- Bombas de Simples Sucção: o rotor possui uma única boca de sucção.
- Bombas de Dupla Sucção: o líquido penetra no rotor pelos dois lados havendo, portanto, duas bocas
de sucção.
Figura 1.6: Rotor de simples (a) e dupla (b) sucção
O rotor de dupla sucção apresenta sobre o de simples sucção a vantagem de proporcionar o equilíbrio
dos empuxos axiais, eliminado a necessidade de um rolamento de grande tamanho para suportar a carga axial
sobre o eixo.
b) Quanto ao número de rotores existentes dentro da carcaça.
- Bomba de simples estágio ou unicelular: a bomba possui um único rotor dentro da carcaça.
- Bomba de vários estágios ou multicelular: a bomba possui dois ou mais rotores dentro da carcaça.
O primeiro rotor aspira o fluído e, ao invés de recalcá-lo, encaminha-o antes aos outros rotores para que
seja novamente energizado e se torne, assim, capaz de atingir maiores alturas.
A bomba de vários estágios, é então, o resultado de uma associação de rotores em série dentro de uma
carcaça.
c) Quanto à pressão desenvolvida
- Bomba de baixa pressão: até 15 mca (1,5 kgf/cm2) aproximadamente;
- Bomba de média pressão: de 15 a 50 mca (1,5 a 5,0 kgf/cm2) aproximadamente;
- Bomba de alta pressão: acima de 50 mca (5,0 kgf/cm2) aproximadamente.

9. d) Quanto à configuração mecânica.
- Bomba com rotor em balanço: o rotor ou rotores são montados na extremidade posterior do eixo de
acionamento que por sua vez é fixado em balanço sobre um suporte de mancais. Este grupo de
bombas também é subdividido em bombas monobloco, onde o eixo de acionamento da bomba é o
próprio orgão acionador e não monoblocos onde eixos de acionamento e orgão acionador são
distintos.
- Bomba com rotor entre mancais: Neste grupo de bombas o rotor ou rotores são montados num eixo
apoiados por mancais em ambas as extremidades e os mesmos se situam entre eles, também é
subdividido em simples e múltiplos estágios.
e) Bombas centrífugas tipo turbina (verticais)
Estas bombas podem ser subdivididas em:
1. bombas de poço profundo;
2. bombas tipo barril;
3. múltiplos ou único estágio;
4. rotores radiais ou semi-axiais;
5. bombas submersíveis para poços artesianos, etc.
1.4 Princípio de funcionamento de uma bomba centrífuga ou radial
Uma bomba centrífuga assemelha-se a um vaso cilíndrico aberto, parcialmente cheio de água e capaz
de, acionado por uma fonte externa, girar em torno de seu eixo de simetria. Esse giro ao atingir o equilíbrio
dinâmico, faz com que o vaso fique com uma velocidade angular (ω=π.n/30) constante e que a água suba pelas
paredes do vaso compondo sua superfície livre um parabolóide de resolução. Quando a velocidade angular ω for
suficientemente grande, a água sobe tanto pelas paredes do vaso, a ponto de descobrir sua região central. Assim
ocorre aumento da pressão sobre as paredes e uma depressão junto ao centro do vaso.
Consideramos agora um vaso cilíndrico fechado e totalmente cheio de água, vaso esse passível de
ligação por tubulação a dois reservatórios: um inferior, a qual se liga pelo centro e outro superior, e ao qual se
liga pela periferia. Ao acionar o vaso girante (rotor), a depressão central aspira o fluido que, sob a ação da força
centrífuga, ganha, na periferia, a sobrepressão que o recalca para o reservatório superior. Teremos , assim, criado
a bomba centrífuga, conforme mostra a figura (1.7)
Uma bomba centrífuga para conseguir entrar em funcionamento (realizar movimento do fluído), deve
estar sempre escorvada (Escorva é o processo no qual evita-se a entrada de ar na bomba, as suas influências serão
explicadas mais adiante), isso significa que a tubulação antes e a própria bomba estão cheias do líquido a ser
bombeado.
Vamos imaginar que a bomba esteja ligada na sua entrada a um tanque à pressão atmosférica, ao ser
acionada a bomba, pelo movimento do impelidor será criado uma pressão menor do que a do tanque na entrada,
fazendo com que o fluído se desloque para dentro da mesma. O fluído dentro do impelidor sofre movimento
centrífugo, o qual é responsável pelo aumento da energia cinética do fluído. Quando o fluído sai do impelidor
atingindo a voluta ocorre uma transformação gradual da energia cinética para energia de pressão, obedecendo-se
a Equação da Conservação de Energia (Bernoulli). A pressão na saída da bomba dependerá da característica da
instalação (tubulação e acessórios) e equipamentos (características de pressão e escoamento).
Figura 1.7: Princípio de funcionamento de uma bomba centrífuga

10. Figura 1.8: Croqui de instalação de uma bomba do tipo centrífuga
Na figura (1.8), é apresentado um croqui de uma instalação de bomba do tipo centrífuga, note que, o
tanque de sução quando está acima do nível da bomba possue sinal positivo (+), isso caracteriza energia
fornecida à bomba.
1.5 Princípio de funcionamento de uma bomba axial
Neste tipo de bomba a força de sustentação provocada pelo escoamento do fluido em torno da palheta
(perfil aerodinâmico) é responsável pelo seu funcionamento. Deve considerar que no movimento vertical de uma
massa do fluido resulta em um vazio (depressão) abaixo da mesma e uma impulsão (sobrepressão) em sua parte
superior, figura (1.9), e ao girar no interior da carcaça da bomba axial, sofrem as palhetas (perfis aerodinâmicos)
um movimento relativo de translação em relação ao fluido, criando uma força de sustentação que produz a
aceleração do fluido no sentido de recalque da bomba.
1.6 Princípio de funcionamento de uma bomba diagonal ou fluxo misto
O funcionamento é devido, em partes, à ação da força centrífuga e à ação da força de sustentação
provocada pelo escoamento do fluido em torno da palheta. Conforme a geometria do rotor se caracteriza como
mais próxima do tipo radial (bombas hélico-centrifugas) ou do tipo axial (bombas helicoidais ou semi-axiais),
passa a ter maior influência a ação da força centrífuga ou a ação da força de sustentação, respectivamente.

11. Figura 1.9: Princípio de funcionamento de uma bomba axial
1.7 Órgãos constitutivos de uma turbobomba
Como vimos uma turbobomba é composta por órgãos principais que são o rotor e o difusor e órgãos
complementares que são os anéis de desgaste, eixo, caixa de gaxetas e selo mecânico, rolamentos , acoplamento
base da bomba e outros. A figura (1.11) mostra uma bomba expandida e a figura (1.12) mostra os componentes
de uma bomba.
1.7.1 O rotor
É o órgão móvel que, acionado pela fonte externa de energia, energiza o fluido, aspirando-o às custas de
uma depressão em sua região central e recalcando-o graças à sobrepressão periférica.
Podem ser classificados em:
Radiais, diagonais e axiais: conforme a trajetória do fluido;
De simples e dupla sucação: conforme recolha o fluido por um lado ou pelos lados;
Rotor fechado, semi-aberto ou aberto: conforme seu desenho mecânico. (figura 1.10)
Rotor fechado: são usados normalmente no bombeamento de liquidos limpos. O rotor possui
discos dianteiro e traseiro e palhetas fixas a ambos. Com esse tipo de rotor evita-se o retorno de
água à boca de sucção, sendo para tal necessário a existência de juntas móveis (anéis de
desgastes) entre a carcaça e o rotor, separando a câmara de sucção da câmara de descarga.
Rotor semi-aberto: possui apenas um disco ou parede traseira onde se fixam as palhetas.
Rotor aberto: as paletas são presas no próprio cubo do rotor.
Existem outros desenhos de rotores visando aplicações especificas: (tabela 1.4)
Figura 1.10: Rotor fechado (a), semi-aberto (b) e aberto (c).

12. Figura 1.11: Desenho explodido de uma bomba
Item Nome da peça Item Nome da peça
01 flange de sucção 02 rotor
03 carcaça ou caixa espiral 04 flange de descarga
05 eixo 06 cavalete
07 caixa de óleo 08 rolamentos
09 retentor 10 tampa da caixa de óleo
11 defletor 12 sobreposta ou aperta-gaxetas
13 estojo de gaxetas 14 cadeado hidráulico
15 gaxetas 16 anel de desgaste traseiro
17 chaveta 18 furos de compensação
19 porca do rotor 20 anel de desgaste dianteiro
Figura 1.12: Componentes de uma bomba centrífuga

13. Tabela 1.4: Variações construtivas dos rotores e suas respectivas aplicações
Referências
•Carvalho, D.F "Instalações elevatórias - Bombas”, IPUC 1977.
•Pfleiderer, C. e Petermann, M. "Máquinas de Fluxo." Editora LTC, Brasil.
•Macintyre, A. J. "Bombas e Instalações de Bombeamento." Ed. Guanabara II, Brasil.

14. Capítulo 2
Princípios Básicos
2.1 Introdução
Para trabalharmos com fluídos devemos inicialmente conhecer algumas propriedades a eles
pertencentes, bases para o nosso estudo. Não iremos aqui desenvolver equações, sendo indicado no final
do capítulo a bibliografia de apoio.
2.2 Escoamento de fluídos:
2.2.1 Fluído
Fluído é toda substância, que se deforma continuamente sobre qualquer esforço tangencial aplicado na
sua superfície livre. Existem algumas denominações de atribuição ao fluído como:
• Fluído ideal, aquele que não possui viscosidade (resistência ao escoamento);
• Fluído incompressível, aquele que não varia o volume sobre aplicação de uma tensão normal à sua área
(pressão).
Para identificarmos os fluídos, descreveremos a seguir algumas de suas propriedades:
2.2.2 Propriedades dos fluídos
1. Peso Específico: relação entre a peso do fluido e o volume ocupado por esse fluido
P
γ= (2.1)
V
onde: γ = peso específico [N/m3]
P = peso do fluído [N]
V = volume [m3];
2. Massa Específica ou Densidade: relação entre a massa do fluido e o volume ocupado por este fluido.
m
ρ= (2.2)
V
onde: ρ = massa específica [Kg/m3]
m = massa do fluído [Kg]
V = volume [m3];
Se pegarmos a massa de um fluído e multiplicarmos pela aceleração da gravidade (g), obtemos o peso
do fluído, portanto podemos escrever a equação abaixo, que relaciona:
γ = ρ⋅g (2.3)
3. Densidade Relativa (d): É a relação entre o peso específico de um fluído de estudo e um fluido de referência
(água a 15ºC no caso de liquido e ar no caso de gás).
γ liquido γ gas
d= = (2.4)
γ agua γ ar
4. Viscosidade: é a propriedade física de um fluído que exprime resistência ao cisalhamento interno, isto é, a
qualquer força que tenda a produzir o escoamento entre suas camadas.
Num fluído real, as forças internas de atrito tendem a impedir o livre escoamento. A viscosidade tem
uma importante influência no escoamento, notadamente através da perda de energia de pressão. A magnitude do
efeito depende principalmente da temperatura e da natureza do fluído. Assim, qualquer valor indicado para a
viscosidade de um fluído deve sempre indicar a sua temperatura, bem como naturalmente a unidade que a
mesma é expressa. Notar que nos líquidos a viscosidade diminui com o aumento da temperatura, enquanto nos
gases ela tende a aumentar.
Newton descobriu que em muitos fluídos a tensão de cisalhamento é proporcional ao gradiente de
velocidade, ou seja:

15. du
τ = µ (2.5)
dy
onde τ é a tensão de cisalhamento [N/m2]
µ é viscosidade dinâmica [ N.s/m2] ou [kg/m.s]
u é a velocidade [m /s]
y é posição [m]
A viscosidade dinâmica ou absoluta exprime a medida das forças internas do fluído e é justamente o
coeficiente de proporcionalidade entre a tensão de cisalhamento e o gradiente de velocidade da Lei de Newton.
Os fluídos que obedecem essa lei, são chamados Fluídos Newtonianos, e os que não a obedecem são chamados
Não-Newtonianos.
Nas aplicações correntes da técnica emprega-se a viscosidade cinemática, expressa pelo quociente do
coeficiente de viscosidade absoluta µ e pela massa específica do fluído.
µ µ ⋅g
ν= = (2.6)
ρ γ
onde: µ = [N.s/m2]
g = [m/s2]
γ = [N/m3]
ν = [m2/s]
No sistema físico (cgs) as unidades são o stoke e o centistoke.
1 stoke (1 st) = 1 cm2/s = 10-4 m2/s
1 centistoke(1 cst) = 0,01 cm2/s = 10-6 m2/s
A viscosidade varia sensivelmente com a temperatura. Na tabela (A.1) são apresentados valores da
viscosidade e outras propriedades da água para várias temperaturas.
2.2.3 Pressão
É a tensão causada por uma força sobre a área onde se aplica esta força.
F
P= (2.7)
A
onde: P = pressão [N / m2];
F = força normal a área [N];
A = área de estudo [m2];
2.2.3.1 Lei de Pascal
" A pressão aplicada sobre um fluído contido em um recipiente fechado age
igualmente em todas as direções do fluído e perpendicularmente às paredes
do recipiente".
É este princípio que permite, por exemplo o funcionamento do macaco
hidráulico, onde uma força pequena F1 é aplicada sobre um embolo de área
pequena, produzindo no fluido uma pressão P, que deve ser igual em todas
as paredes do recipiente, assim, no êmbolo de maior área, a força resultante Figura 2.1: Princípio de
F2 é tão maior quanto maior for a relação entre as áreas dos êmbolos. funcionamento do macaco
hidráulico.
2.2.3.2 Pressão absoluta e pressão manométrica
Pressão absoluta (pabs) é a escala de pressão medida a partir do zero absoluto ou vácuo, sendo a soma da
pressão atmosférica local (patm) mais a pressão manométrica (pman) também chamada de relativa. Sua equação é:
pabs = patm + pman (2.8)
2.2.3.3 Teorema de Stevin (Manometria)

16. "A diferença de pressão entre dois pontos de um fluído em equilíbrio é
igual ao produto do peso específico do fluído pela diferença de cotas entre dois
pontos". Esse Teorema define a equação básica da estática para dois pontos em
um fluído.
pb − pa = γ ⋅ h (2.9)
A diferença de pressão absoluta entre a superfície livre e um ponto
dentro do reservatório é:
p a = p atm + γ ⋅ h (2.10)
Vasos comunicantes: pontos que estejam no mesmo nível estão sujeitos a mesma
pressão.
Figura 2.2: Teorema de Stevin
2.2.3.4 Carga de Pressão ou Altura da Coluna de Líquido
Carga de pressão é a altura na qual pode ser elevada uma coluna de líquido quando está sob influência
de uma certa pressão.
P
h= (2.11)
γ
onde: h = altura de coluna de líquido [m];
P = pressão [Pascal];
γ = peso específico [N / m3];
É usual, quando se trata de especificação de bombas, relacionar a pressão necessária em metros de
coluna de fluído (mcf), como a maioria das bombas são ensaiadas com água a unidade de pressão mais utilizada
é metros de coluna d água (mca).
2.2.3.5 Pressão de Vapor
Para caracterizar o estado de uma substância pura são necessárias duas propriedades independentes.
Para um gás ou mesmo um líquido, normalmente Pressão e Temperatura são propriedades independentes,
entretanto, na região de mudança de fase elas são relacionadas, e portanto não são independentes. Portanto, para
uma determinada substancia pura, para cada temperatura haverá um pressão na qual a coexistência das fases
líquida e vapor. A essa pressão damos o nome de Pressão de Vapor. A tabela (A.1) traz valores de pressão de
vapor para a água nas temperaturas mais usuais de trabalho.
2.2.4 Escoamento
Devemos inicialmente definir algum termos relacionados com escoamento como:
a) Regime Permanente: é quando no escoamento as propriedades do ponto (ex.: pressão, temperatura, etc) não
variam com o tempo;
b) Regime Laminar: é aquele no qual os filetes de líquido são paralelos entre si e as velocidades em cada ponto
são constantes;
c) Regime Turbulento.: é aquele no qual as partículas apresentam movimentos variáveis, com diferentes
velocidades em modulo e direção de um instante para outro;
Para se caracterizar o tipo de escoamento, é utilizado o número de Reynolds (Re), que é definido como
a resistência que os líquidos oferecem ao escoamento é um fenômeno de inércia - viscosidade, que exprime a
relação entre as forças de inércia e as forças de atrito interno (forças de cisalhamento) atuantes no escoamento.
v.D
Re = (2.12)
ν
onde:
Re = número adimensional
D = diâmetro interno do tubo [m]
v = velocidade média [m/s]
ν = viscosidade cinemática [m2/s]
A grande importância do número de Reynolds reside em que permite entre inúmeras outras aplicações:

17. 1. Estabelecer a lei de analogia entre dois encanamentos.
2. Caracterizar a natureza do escoamento
3. Calcular o coeficiente de perda de carga.
Quando os dispositivos de escoamento forem semelhantes, o regime do escoamento será o mesmo
sempre que o número de Reynolds for o mesmo. Isto dá maior importância para estudos e ensaios de laboratório,
quando se pode, por exemplo, usar ar ao invés de água, água ao invés de outros líquidos.
Suponhamos que temos dois encanamentos de igual diâmetro, igual rugosidade, sendo que em um
escoa água e em outro ar. Como a viscosidade cinemática da água é da ordem de 15 vezes maior que a do ar, a
velocidade do escoamento do ar deverá ser da ordem de 15 vezes maior que a da água, para manter o mesmo
número de Reynolds e com isso o coeficiente de perda de carga também o será.
Em outras palavras, podemos realizar o escoamento usando ar, desde que com velocidades l5 vezes
maior do que se teria de empregar no caso da água.
2.2.4.1 Caracterização da natureza do escoamento
O escoamento permanente pode ser laminar ou turbulento.
Experiência de Reynolds:
Deixando-se água escorrer por um cano transparente juntamente com um líquido colorido, forma-se um
filete desse líquido. O movimento da água está em regime laminar.
No escoamento laminar ou regime laminar em um tubo cilíndrico, as extremidades dos vetores
velocidades das partículas numa dada seção de escoamento formam uma superfície parabólica, e a velocidade
máxima se verifica no eixo do tubo. A velocidade máxima da corrente é cerca de 1,5 a 2 vezes a velocidade
média. Junto às paredes, as velocidades das partículas é praticamente nula.
O regime de escoamento laminar ocorre nos tubos capilares, no movimento de óleo em oleodutos, sabão
em tubos, etc.
Voltando à experiência de Reynolds, à medida que se aumenta a vazão da água abrindo-se a torneira, o
filete vai se alterando podendo chegar a difundir-se na massa líquida, atingindo-se portanto o escoamento
turbulento.
No escoamento turbulento, devido à natureza do movimento das partículas ocorrem deslocamentos
transversais, produz-se uma distribuição uniforme das velocidades.
Mesmo no escoamento turbulento, junto às paredes ocorre um filme laminar cuja espessura é muito
pequena e inversamente proporcional ao número de Reynolds (camada limite laminar).
Para se determinar o tipo de escoamento em uma canalização, calcula-se o número de Reynolds e
compara-se o valor obtido com os seguintes valores:
Re ≤ 2000 ---> Movimento Laminar
2000 ≤ Re ≤ 4000 ---> Zona de Transição
Re ≥ 4000 ---> Movimento Turbulento
Exemplo:
Mostrar que na prática o movimento da água em encanamento é sempre turbulento.
Resolução:
A velocidade média em encanamentos de água geralmente varia em torno de 0,90 m/s.A temperatura
admitida de 20ºC e diâmetro de 38mm.
v.D 0.90 ⋅ 0.038
Re = = = 33962 onde.: v = 0,90 m/s
ν 0.000001007
D = 0,038 m
ν = 0,000001007 m2/s (tabela A.1)
Re = 33.962 (Este valor é bem superior a 4.000, define o movimento turbulento)
2.3 Princípios de conservação:

18. 2.3.1 Conservação da massa
A conservação da massa apesar de ser um fato comprovado (para sistemas sob o prisma das Leis de
Newton), sua equação para volume de controle foi deduzida a partir do teorema de transporte de Reynolds e a
idéia de sistema.
Para regime permanente, na sua forma integrada podemos escrevê-la da seguinte maneira:
∑ m e= ∑ m s
(2.13)
onde: ∑ me = somatória das massas na entrada do volume de controle [Kg/s];
∑ ms = somatória das massas na saída do volume de controle [Kg/s];
Se pegarmos a equação anterior e dividirmos pela massa específica do fluído nas entradas e saídas (para
fluídos incompressíveis) obtemos:
 Volume   Volume 
  =  (2.14)
 Tempo  e  Tempo  s
ou
Q e = Qs (2.15)
onde: Qe = vazão volumétrica de entrada [m3/s; m3/h]
Qs = vazão volumétrica de saída [m3/s; m3/h]
Vazão pode ser interpretada como o fluxo ou velocidade de fluído passando pela superfície ou área do
volume de controle, logo:
Q = v ⋅A
(2.16)
onde:
v = velocidade com o fluído cruza a superfície [m/s];
A = superfície ou área de estudo do volume de controle[(m2];
Portanto a equação da continuidade em termos de fluxo volumétrico fica:
v e . Ae = vs . As (2.17)
2.3.2 Conservação da energia
2.3.2.1 Equação de Bernoulli
A equação de Bernoulli é um caso particular da equação de Euler, sendo usada para fluídos
incompressíveis e em regime permanente e sem atrito. A partir dela podemos dizer que a energia total num
ponto 1 de uma linha de corrente é igual a energia total a um ponto dois na mesma linha de corrente. Bernoulli
confirma a conservação de energia ao longo de um escoamento.
Energia totalponto1 = Energia totalponto2 (2.18)
A energia de um ponto é composta pelas energias abaixo relacionadas:
a) Energia cinética ou energia devido ao deslocamento
v2
Ec = (2.19)
2g
onde: Ec = energia cinética [m.c.f.];
v = velocidade [m/s];
g = aceleração da gravidade [m/s2];
b) Energia de pressão ou energia mecânica
p
Ep = (2.20)
γ
onde: Ep = energia de pressão [m.c.f.];
p = pressão do líquido [Pa];
γ = peso específico do fluído [N/m3];

19. c) Energia potencial ou de posição
Epz = Z (2.21)
onde: Epz= energia potencial [m.c.f.];
Z = altura em relação ao referencial [m];
Portanto a equação de Bernoulli fica:
v2 p
Ec + Ep + Epz = constante = + +Z (2.22)
2g γ
Se utilizarmos a equação de Bernoulli para dois pontos obtemos:
2 2
v 1 p1 v 2 p2
+ + Z1 = + + Z2 (2.23)
2g γ 2g γ
Quando consideramos a troca de calor e o trabalho envolvido em regime permanente temos a
expressão:
q W  v2 p2
  v 1 p1
2

− = 2
+ + Z2 −  + + Z1 (2.24)
mg mg  2g γ
  2g γ 
onde:
q = fluxo de calor trocado [W]
W = potência trocada [W]
m = fluxo de massa que atravessa o volume de controle [kg/s]
2.4 Perdas de carga
Como foi observado no item anterior, na equação de Bernoulli para fluídos ideais a energia se conserva
ao longo do escoamento, mas com os fluído reais existe um perda de energia devida a resistências do tipo
internas (devido a viscosidade) e do tipo externas (devido ao atrito do fluído contra parede, variações de
velocidades e mudanças de direção), a essa resistência daremos o nome de Perda de Carga . Devemos portanto
adicioná-la na equação de Bernoulli para que a energia total entre dois pontos se conserve.
q W  v2 p2
  v1 p1
2

− = 2
+ + Z2 −  + + Z1 + ∆H (2.25)
mg mg  2g γ
  2g γ 
onde: ∆H = perda de carga entre dois pontos (unidade m.c.f.);
As perdas de carga estão classificadas em:
a) Perdas de carga ao longo das canalizações; ∆Hc
b) Perdas de carga localizadas; ∆Hd
2.4.1 Perdas de carga ao longo das canalizações ou distribuídas
A resistência ao escoamento ao longo das canalizações depende do comprimento, diâmetro do tubo, da
velocidade e viscosidade do fluído, da rugosidade das paredes do tubo, não dependendo da posição do tubo e nem
da pressão interna.
Existem várias formulas empíricas para o cálculo da perda de carga ao longo das canalizações, porém
veremos apenas a fórmula universal, que é válida para qualquer líquido, e é empregada no chamado Método
moderno ou racional.
Darcy e Weissbach chegaram a esta expressão:
L v2
∆H c = f (2.26)
D 2g
onde: f = coeficiente de atrito [adimensional];
L = comprimento do tubo [m];
D = diâmetro do tubo [m];
v = velocidade média de escoamento [m/s];
g = aceleração da gravidade [m/s2];
∆H = perda de carga [m];

20. A velocidade do fluido de escoamento, segundo a equação da continuidade aplicada a dutos circulares, é
dada por:
4Q
v= (2.27)
πD 2
Em dutos não circulares o diâmetro será o diâmetro equivalente (Deq)., e é calculado por:
4A
D eq = (2.28)
P
onde: A = área transversal do duto [m2];
P = perímetro da seção transversal do duto [m].
Utilizando esta equação para um duto de seção circular, temos que Deq = D.
Para um duto de seção retangular de lados a e b, temos que Deq = 2ab/(a+b)
2.4.1.2 Determinação do coeficiente f
A determinação do coeficiente f leva em consideração se o escoamento é laminar ou turbulento:
a) Escoamento Laminar - Re 2.000
O coeficiente f não depende da rugosidade do escoamento, mas apenas do número de Reynolds
64
f= (equacao de Poiseuille) (2.28)
Re
A equação de perda de carga para regime laminar fica:
L vν
∆H c = 32 (2.29)
D2 g
onde: ν = Viscosidade cinemática [m2/s]
Esta fórmula serve para qualquer líquido e qualquer tubo, independente do material, do estado e da
rugosidade das paredes. Como se vê, no escoamento laminar a perda é sempre proporcional, à velocidade.
b) Escoamento Turbulento - Re 4.000
Para os escoamentos turbulentos, o coeficiente de atrito f é uma função de Re e da rugosidade do
material ε ou k, ou da rugosidade relativa (ε/D ou k/D). a rugosidade relativa pode ser obtida diretamente da
figura (B.1) ou através dos valores da rugosidade absoluta pela tabela (A.3).
Outra forma f é através da forma iterativa através da equação transcendental apresentada por Colebrook
:
1
f = { }2 (2.30)
9,3
1,14 + 2 log( D ) - 2 log[1+
ε ε
]
Re( D ) f
Churchill propõe a seguinte equação para o cálculo de f:
8 12 1
f = 8.[( ) + 3/ 2
]1/12 (2.31)
Re (A + B )
1 16 37530 16
onde: A = [2,457. ln( )] e B = [ ] A forma direta de obter f
(7 / Re ) + 0,27.( ε / D)
0,9
Re
é pelo diagrama de Moody (figura B.2), onde apresenta em abcissas o número de Reynolds (Re), e a esquerda o
coeficiente de atrito f, ambos em escalas logarítmicas. Pode ser notado que o limite do escoamento laminar é
considerado igual a 2.000.
a) Para Re 2000, regime Laminar, usa-se a reta A de Poiseuille;

21. b) Para Re compreendido entre 2000 e 4000 tem-se o regime instável ou crítico de transição do laminar ao
turbulento, e o fator de resistência oscila em torno de uma curva que pode ser considerada independente da
rugosidade.
c) Para Re 4000, o regime é turbulento e temos uma curva representativa de f para cada viscosidade.
A linha D se aplica aos tubos lisos. A partir da curva E, para a direita verifica-se que f não depende
mais de Re, mas apenas da rugosidade relativa ε/d, isso ocorre devido a camada limite laminar se tornar menor
que as asperezas do tubo, devido ao regime de completa turbulência.
No diagrama de Moody, existe um termo ε/d, que relaciona a rugosidade que a tubulação possui com o
seu diâmetro. Pode ser notado que quanto maior a relação ε/d maior o valor do fator f e portanto maior a perda
de carga.
Exemplo:
Num oleoduto são bombeados 190 l/s de óleo cru a temperatura de 16ºC (ν = 1,06 x 10-5 (m2/s) ),
sabendo-se que o encanamento é constituído por um conduto novo de aço comercial de 0,450m de diâmetro e
com um comprimento de 1.000m. Calcular a perda de carga.
Resolução:
pelo enunciado
Q = 190 l/s = 0,190 m3/s;
L = 1000 m;
D = 0,45 m
ν = 1,06 x 10-5 (m2/s)
1º passo --- v = Q/A
A = (π D2)/4 = ( π 0,452)/4 = 0.159 m2
v = (0,190/0.159) = 1,19 m/s
2º passo --- Re = (V.D)/ν
Re = (1,19 0,45)/ 1,06 x10-5 Re = 5,05 x 104 (turbulento)
30 passo --- Pela tabela de ε/d (A.3), obtemos ε/D = 0,0001;
40 passo --- com os valores de ε/D e Re entramos no Diagrama de Moody (figura A.2)e obtemos
f = 0,021
50 passo --- ∆Hc = f (L/D) (V2/2g)
∆Hc = 0,021 (1000/0,45) (1,192/(2 . 9,8)) = 3,37 m
2.4.1.2 Perda de carga em canalizações de PVC
Para cálculo da perda de carga contínua em tubulações de PVC pode ser usado diretamente, a figura
(B.3).
2.4.1.3 Perda de carga em tubulações de ar
Neste caso podemos usar a figura (B.4) para calcular a perda de carga neste dutos
Pode-se também utilizar a figura (B.4) para calcular a perda de carga em dutos não circulares utilizando
o valor de Deq calculado desta forma, desde que o outro parâmetro utilizado como entrada no ábaco seja a
velocidade, calculada como V = Q/A.
No caso de querermos entrar na figura (B.4) para dutos não circulares com o valor da vazão
diretamente, devemos utilizar um diâmetro equivalente para atrito (Deq.f), que para dutos retangulares é calculado
segundo a equação:
0,625
(ab )
D eq.f = 1,30x 0,25
(2.32)
(a + b )
Com o valor de Deq.f calculado dessa forma, a figura (B.4) pode ser utilizado diretamente para o cálculo
da perda de carga, desde que se entre com o valor da vazão, pois com este procedimento, o valor de velocidade
indicado na carta não corresponde à velocidade no duto retangular.

22. A velocidade real deve ser obtida de V = Q/A.
2.4.2 Perdas de carga localizadas
As perdas de cargas localizadas, também chamadas de perdas singulares são ocasionadas por mudanças
de direção e ou mudança de seção no escoamento. Estas mudanças ocasionam turbilhonamento e, devido à
inércia, parte da energia mecânica disponível se converte em calor se dissipando, resultando portanto numa
perda de energia ou perda de carga.
Exemplo de mudança de direção nas tubulações temos:
curvas;
cotovelos;
tês;
junções, etc.
Exemplo de mudanças de seção de escoamento nas tubulações temos:
entrada de tubulações;
saídas de tubulações;
válvulas;
reduções;
diafragmas, etc.
este tipo de perda deve ser somado a perda de carga distribuída.
Para calcular a perda de carga localizada existem dois métodos:
2.4.2.1 Método direto
A perda de carga localizadas pode ser dada diretamente por:
v2 v2 v2
∆H d = K = C c,s = C c ,b (2.33)
2g 2g 2g
onde: K = característica do acessório (tabela A.4)
Cc,s = característica de junções ou bifurcações no duto principal (tabela A.5 à A.10)
Cc,s = característica do junções ou bifurcações no duto secundário (tabela A.5 à A.10)
Para fins de aplicação prática pode-se considerar constante o valor de K para determinada singularidade
desde que o escoamento seja turbulento, independentemente do diâmetro da tubulação, da velocidade e da
natureza do fluído.
2.4.2.2 Método dos comprimentos equivalentes:
Uma canalização que possui ao longo de sua extensão diversas singularidades, eqüivale, sob o ponto de
vista de perdas de carga, a um encanamento retilíneo de comprimento maior sem singularidades.
Pensando assim, os problemas que envolvem perda de carga são bastante simplificados.
O método consiste em adicionar à extensão da canalização, para efeito de cálculo, comprimentos tais
que corresponda à mesma perda de carga que causariam as peças especiais existentes na canalização.
As tabelas (A.11e A.12) apresentam os comprimentos equivalentes a perdas localizadas em metros de
canalização retilínea, baseada na fórmula de Darcy.
O encanamento com um certo comprimento que possui um registro ao longo de sua linha terá uma
perda de carga que será a soma da perda ao longo da canalização mais a perda de carga no registro.
O mesmo encanamento desprovido do registro poderá apresentar a mesma perda de carga se seu
comprimento foi convenientemente aumentado.
Procedimento para cálculo de perda de carga, com perdas localizadas e perdas ao longo da canalização
simultaneamente.
O procedimento é calcular as perdas localizadas com as perdas distribuídas simultaneamente, na
equação geral.

23. L v2
∆H = f (2.35)
D 2g
Para isso o comprimento L será a soma do comprimento da tubulação reta (Lc), e os comprimentos
equivalentes (Leq) representante das peças, válvulas e conexões existentes ao longo da tubulação.
Exemplo: Calcule a altura h2 ( figura abaixo) suficiente para manter a vazão de 0,2 litros/ seg. no chuveiro (7).
Inicialmente considere o encanamento de aço galvanizado de ½” (12,7mm).
Resolução:
Usaremos o método do comprimento equivalente
Número acessório Leq (tabela A.11) Total
1 entrada na canalização 1 x 0,2 0,2
2,3,4,6 cotovelo 90º 4 x 0,4 1,6
5 registro gaveta 1 x 0,1 0,1
7 chuveiro (distância do solo) 1 * 2,0 2,0
Leq = 3,9
Comprimento dos trechos retos de tubos:
Lc = 10,0 + 2,0 + 1,0 + 1,0 + 0,5 = 14,5 m
L = Lc + Leq = 14,5 + 3,9 = 18,4m
Logo, o valor de L que usaremos na equação (2.35) da perda de carga será de L = 18,4m.
Para determinar o valor de f precisamos do número de Reynolds (Re) e da rugosidade relativa (ε/d)
como a vazão foi dada e vale 0,2 l/s = 0,2 x 10-3 m3/s;
e o diâmetro da tubulação ½” (12,7mm). A área correspondente é de 1.27 x10-4 m2.
A velocidade na tubulação será de v = Q/A = 1,58 m/s
pela tabela (A.1) ν = 1,06 x 10-5 (m2/s) (temperatura de 16ºC);
Re = vD/ν = 1891,61 portanto regime laminar f = 64/Re = 0,03383
L v2 18,4 1,58 2
∆H = f = 0,03383 = 6,23704 m
D 2g 12,7 × 10 − 3 2 × 9,81
aplicando na equação (2.25) como não a troca de calor e nem trabalho a equação fica:

24.  v 1 p1
2
  v2 p 
 + + Z1 =  2 + 2 + Z2 + ∆H
 2g γ   2g γ 
substituindo os dados
 02   1,58 2 
 + h2  =  + 2 + 6,2374 = 8,36428m
 2g   2 × 9,81 
Referências
Fox e McDonalds, ”Introdução à Mecânica dos Fluidos”, 4a ed., Ed. Guanabara

25. Lista de exercício nº1
1-) Uma placa infinita, se movimenta paralelamente a uma superfície horizontal fixa. Entre as duas
superfícies existe um fluído com viscosidade de µ = 7,2x10-3 poise (1 poise = 0,1kg/ms). Admitindo-se
que o perfil de velocidade é linear com valor de 0,5m/s, determine:
a-) A Tensão de cisalhamento e a sua direção de aplicação, referente a placa móvel;
b-) A viscosidade cinemática do fluído (d= 0,8);
2-) Um eixo cilíndrico de diâmetro 80mm, gira no interior de um mancal de diâmetro 82mm. A folga
entre o eixo e o mancal é preenchida pôr óleo com viscosidade dinâmica µ = 7,2x10-3 Ns/m2. Determine a
potência necessária para que o eixo gire com rotação constante n = 1200rpm. Supor que a distribuição de
velocidade na folga é linear.
3-) Um mergulhador, mergulha no mar (d=1,025) e no rio (d=0,998), até a profundidade de 50 metros.
Determine a pressão relativa e absoluta nas duas condições e verifique em qual local ele esteve sujeito a
maior pressão. Em ambos os locais, a pressão atmosférica é de 101,3kPa e g= 10m/s2.
4-) Determine a pressão no ponto A em Pa manométrica devida à deflexão do mercúrio, d=13,6, no
manômetro em da figura abaixo.
5-) Água escoa pelas tubulações A e B, um manômetro duplo U foi conectado entre as duas tubulações
conforme apresentado na figura abaixo. Determinar a diferença de pressão entre as duas tubulações.
Dados: dHg =13,6; dóleo = 0,8; dH20 =1,0; γH20 = 10000N/m2 . As leituras no manômetro são dadas em cm.

26. Capítulo 3
Altura Manométrica do Sistema
Define-se a altura manométrica de um sistema elevatório como sendo a quantidade de
energia que deve ser absorvida por unidade de peso de fluído que atravessa a bomba, energia
esta necessária para transportar o fluído do reservatório de sucção para o reservatório de
descarga, a diferença de pressão entre os dois reservatórios e a resistência natural que as
tubulações e acessórios oferecem ao escoamento dos fluidos (perda de carga)com uma
determinada vazão.
No sistema que estudaremos esta energia será fornecida por uma bomba centrífuga e a altura
manométrica é um parâmetro fundamental para a escolha da mesma.
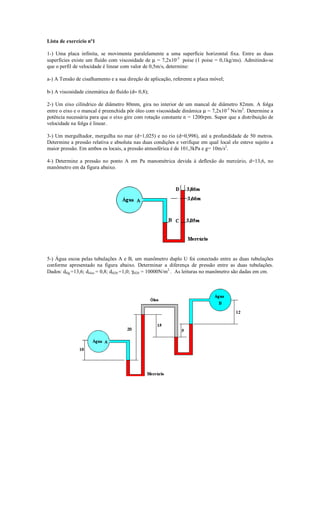
Figura 3.1: Distribuição ao longo de um sistema de bombeamento das alturas manométricas de sucção, recalque,
geométrica e total.
p rd - p rs
H man =Hg + + ∆H (3.1)
γ
onde: Hs = altura de sucção
Hr = altura de recalque
Hg = Hs + Hr (desnível geométrico)
Hm = altura manométrica [m]
prd = pressão no reservatório de descarga [N/m2]
prs = pressão no reservatório de sucção [N/m2]
γ = peso específico [N/m3]
∆H = perda de carga em m.c.f.
Quando ambos os reservatórios são abertos e sujeitos, portanto, à pressão atmosférica, temos:
prd = prs = patm (3.2)

27. e a equação (3.1) fica:
H man = H g + ∆H (3.3)
3.1 Medição direta da altura manométrica
Numa instalação de bombeamento em funcionamento, poderemos obter a grandeza da altura
manométrica diretamente da própria instalação.
Poderá haver a necessidade de variar a vazão para atendimento do consumo. Esta variação de vazão,
processada através da variação da abertura da válvula de recalque, torna, variável o valor da altura manométrica.
Com a colocação de um manômetro na sucção e na descarga da bomba é possível medir diretamente a
altura manométrica desenvolvida pela bomba, qualquer que seja a vazão recalcada (ver figura. 3.2).
Se a bomba tem sucção positiva (está montada acima da linha de nível do reservatório de sucção) a
expressão é:
pd + ps
Hman = + Zds (3.4)
γ
pd
ps
Figura 3.2: Medição direta da altura manométrica
onde: pd = pressão lida no manômetro colocado na descarga [Pa];
ps = pressão lida no manômetro colocado na sucção [Pa];
γ = peso específico do fluído [N/m3];
Zds = é a diferença de cota entre as linhas de centro dos dois manômetros colocados na sucção e na
descarga.
Figura 3.3: Sucção positiva Figura 3.4: Sucção negativa
Se a bomba tem sucção negativa (está montada abaixo do nível do reservatório de sucção) a bomba está
afogada e a expressão da altura manométrica será
pd
Hman = − ( H gs − Zds ) (3.5)
γ
onde: Hgs = desnível do reservatório de sucção
Outra forma de obter a altura manométrica é pela diferença entre a altura manométrica de recalque
(descarga) (Hmd) e da a sucção (Hms).

28. H man = H md - H ms (3.6)
3.2 Altura manométrica de sucção
É a soma da altura geométrica de sucção (Hgs), a pressão atuando no reservatório de sucção (prs) e a
perda de carga na sucção (∆Hs).
p rs
H ms = H gs + +∆ Hs (3.7)
γ
O termo Hgs pode ser positivo ou negativo, dependendo do tipo de instalação da sucção. A seguir serão
apresentados alguns tipos.
a) Sucção Positiva
É quando o nível do líquido no reservatório de sucção está abaixo da linha de centro da bomba. Neste
caso o termo Hgs é positivo (figura 3.3). É necessário usar uma válvula de retenção com crivo no início da
tubulação de aspiração, a “válvula pé” impede o retorno do fluido, quando a bomba está parada.
b) Sucção Afogada ou Negativa
É quando o nível do líquido no reservatório de sucção está acima da linha de centro da bomba. Neste
caso o termo Hgs é negativo (figura 3.4). Neste caso não há necessidade de válvula de pé com crivo desde que o
nível da água permita encher completamente a bomba.
3.3 Altura manométrica de descarga
É a soma da altura geométrica de descarga (Hgd), a pressão atuando no reservatório de descarga (prd) e a
perda de carga na descarga (∆Hd).
p rd
H md = H gd + +∆ H d (3.8)
γ
3.4 Curvas características do sistema
Os sistemas de bombeamento são compostos por diversos elementos tais como bombas, tubulações,
válvulas e acessórios, sendo todos necessários para obter-se a transferência do fluído de um ponto para outro.
Os parâmetros Vazão (Q) e Altura Manométrica (Hman) são fundamentais para o selecionamento da
bomba adequada para um sistema.
Muitas vezes, no entanto, é necessário conhecer-se não somente um ponto de operação do sistema (Q e
Hman) mas a Curva Característica do Sistema, o comportamento ou relação entre a vazão e a altura
manométrica. Esta curva é muito importante para se conhecer exatamente o ponto de trabalho da bomba.
3.4.1 Levantamento da curva do sistema
A curva característica do sistema é levantada, plotando-se a altura manométrica em função da vazão do
sistema, conforme indicado a seguir:
1º) passoTomar uma das fórmulas para obtenção da altura manométrica;
2º) passoFixar algumas vazões dentro da faixa de operação do sistema. Sugere-se fixar cerca de cinco pontos,
entre eles o ponto de vazão nulo (Q=0) e o ponto de vazão do projeto (Q=Qproj);
3º) passoCalcular a altura manométrica corresponde a cada vazão fixada obtendo-se a seguinte tabela:
Q (m3/h) Hman (m.c.f.)
Q1 = 0 Hman1 =
Q2 = Hman2 =
Q3 = Hman3 =
Q4 = Qproj Hman4 =
Q5 = Hman5 =
4º) passo Plotar os pontos obtidos num gráfico Q x Hman, obtendo-se assim a curva do sistema,
conforme ilustrado a seguir:

29. Para o projeto de um sistema de tubulações, dimensiona-se o diâmetro dos dutos pela vazão de
projeto, e assim, faz-se o cálculo da perda de carga somente para esta vazão. Para não termos que
recalcular para cada uma das vazões fixadas acima novamente a perda de carga, podemos trabalhar um
pouco com as equações da altura manométrica (3.1) e da perda de carga (2.35), rearranjando-as da
seguinte forma:
Prd - Prs L v2
H man = Hg + + f (3.9)
ρg D 2g
Lembrando que Q = v.A e A = π D2/4
substituindo-se na equação (3.9), obtemos:
Prd - Prs L Q2
H man = Hg + + 2f 5 (3.10)
ρg D g
Nesta equação, os dois primeiros termos podem ser considerados constantes, e agrupados em uma
única constante C1 e o termo multiplicando Q2, se considerarmos que f não varia com a vazão (região
plenamente turbulenta), pode ser considerada uma constante C2 , assim, a equação fica sendo a de uma
parábola:
2
H man = C1 + C2 .Q (3.11)
Os valores de C1 e C2 podem ser determinados a partir dos pontos de vazão nula e vazão de
projeto:
Prd - Prs
Para Q = 0 temos H man ,0 = Hg + = C1 (3.12)
ρg
2
Para Q = Qproj temos H man ,proj = C1 + C2 .Q proj
C2 =
(H man , proj ) . = 2f
− C1 L
(3.13)
2
Q proj D5g
Exemplo:
Determine a curva do sistema do esquema abaixo,

30. Resolução:
1) determinação da Hman do sistema
2
H man = C1 + C2 .Q (3.11)
onde:
Prd - Prs
C 1 = Hg + = H man , 0
ρg
pela figura Hg = 10 m
prd = prs = patm
portanto
C 1 = Hg = 10 m
e C2 é pela equação (3.13)
L
C2 = 2 f
D5g
Dados:
vazão de 0,2 litros/ seg. 0,2 x 10-3 m3/s;
aço galvanizado de ½” (12,7mm).
acessório Leq (tabela A.11) Total
Sucção
cotovelo 90º 2 x 0,4 0,8
Descarga
válvula de retenção (leve) 1 x 1,1 1,1
registro gaveta 1 x 0,1 0,1
cotovelo 90º 1x 0,4 0,4
Leq = 2,4
Comprimento dos trechos retos de tubos: Lc = 2+1+10 = 13 m
L = Lc + Leq = 13 + 2,4 = 15,4m
A área correspondente é de 1.27 x10-4 m2.
A velocidade na tubulação será de v = Q/A = 1,58 m/s
pela tabela (A.1) ν = 1,06 x 10-5 (m2/s) (temperatura de 16ºC);
Re = vD/ν = 1891,61 portanto regime laminar f = 64/Re = 0,03383
L 15,4
C2 = 2f = 2 × 0,03383 = 321488248,1
5
D g (12,7 × 10 −3 )5 × 9,81
portanto a expressão da altura manométrica será:
H man = C1 + C2 .Q = 10 + 3214882481 Q
2 2
,
fornecendo valore de Q e obtendo H termos a tabela abaixo, cuidado Q na expressão esta em m3/s e na tabela esta
em m3/h.
Q (m3/h) Q (m3/s) Hman (m.c.f.)
Q1 = 0 Q1 = 0 Hman1 =10
Q2 = 0,1 Q2 = 0.000028 Hman2 =12,248
Q3 = 0,5 Q3 = 0,0014 Hman3 =16,202
Q4 = Qproj =0,72 Q4 = Qproj = 0,00020 Hman4 =22,859
Q5 = 1 Q5 = 0,00028 Hman5 =35,204
agora e só plotar Hman (mcf) em função de Q (m3/h)

31. teremos a curva do sistema
3.5 Associação de sistemas
Existem casos particulares de traçado da característica do sistema que devem ser ressaltados. São
eles:
3.5.1 Associação em série:
Consiste na combinação de diâmetros diferentes na mesma linha de descarga.
Quando estiver fluindo pelo sistema a vazão Q, o valor da altura manométrica será a soma das
alturas manométricas correspondentes de cada sistema, obtendo-se a curva do sistema resultante.
A figura (3.6) mostra um esquema de uma instalação com diâmetros diferentes, onde escoa
vazão Q, sejam ∆H1 a perda de carga no recalque no trecho com diâmetro φ, e ∆H2 a perda de carga no
recalque no trecho com diâmetro φ’. A perda de carga na sucção será representada por ∆Hs. A perda de
carga total será a soma das perdas de carga nos trechos com diâmetro φ e φ’e a perda de carga na sucção
∆H = ∆H s + ∆H 1 + ∆H 2 (3.14)
A curva característica total do sistema será determinada por pontos, somando-se, para cada
vazão, as perdas nos dois trechos. (figura 3.7). Neste caso desprezou a perda de carga na sucção devido ao
comprimento da linha e o número de acessórios ser pequeno. Estas perdas estão representadas,
separadamente, pelas curvas que partem da origem do sistema cartesiano e, somadas, dão, para cada
vazão, a perda de carga total.
Figura 3.5: Representação de sistemas em série

32. Figura 3.6: Linha de recalque com diâmetro diferentes Figura 3.7: Curva do sistema na combinação de
diâmetros
3.5.2 Associação em paralelo:
Consiste na combinação de várias descargas independentes derivando-se da mesma linha de
descarga. (figura 3.8)
Quando estiver fluindo pelo sistema a vazão Q, para cada altura manométrica, somam-se as
vazões correspondentes em cada sistema, obtendo-se a curva do sistema resultante.
Como já visto nos dois casos anteriores, o procedimento para o levantamento da curva do sistema
resultante consiste inicialmente no levantamento da curva de cada sistema independentemente (como se
não existisse nenhum outro) e em seguida obtém-se a curva resultante do sistema.
Considere-se a instalação com duas descargas independentes mostradas na figura (3.9), onde:
D: ponto de bifurcação da linha de recalque;
Ho: desnível até o reservatório B;
Ho’: desnível até o reservatório C;
QA: vazão aspirada e recalcada pela bomba;
QB: vazão encaminhada ao reservatório B
Qc: vazão encaminhada ao reservatório C
Figura 3.8: Associação de sistemas em paralelo

33. Duas hipóteses, então, se nos apresentam:
Primeira hipótese: a bomba instalada no
sistema, ao operar a vazão QA, desenvolve
uma altura HoHmanHo’.
Neste caso, evidentemente, o liquido não
atingirá o reservatório C e QB = QA ( toda
a vazão recalcada será encaminha ao
reservatório B).
Várias curvas de bombas, todas elas,
porém, interceptando a curva do sistema
AB, antes do ponto E (ponto acima do
qual Hman Ho’).(figura 3.10)
Assim, quando a curva da bomba
interceptar a do sistema à esquerda de E,
só haverá bombeamento para (B).
Segunda hipótese: a bomba instalada no
sistema, ao operar a vazão QA, desenvolve
uma altura Hman Ho’.
Figura 3.9: Linha de recalque com duas descargas diferentes
Figura 3.11: Segunda hipótese Hman Ho’
Figura 3.10: Primeira hipótese Ho Hman Ho’
É, exatamente, o caso no qual a intersecção da curva totalizada do sistema com a curva da bomba
se dá à direita do ponto E (figura 3.11).
Esta curva do sistema se constitui de dois trechos: até o ponto E só leva em conta a perda de carga
relativa ao trecho reservatório A para o reservatório B e, após o ponto E, passa a considerar a perda de
carga da bifurcação D ao reservatório C (para a vazão QC).
Na figura (3.11): A curva DC representa a variação da perda de carga com a vazão no trecho
ponto D - reservatório C. O trecho EP da curva totalizada é obtido, somando-se, para cada valor de altura
(Hman) desenvolvida Hman Ho’, os valores de QC e QB (lidos para o valor de Hman Ho’ nas curvas dos
sistemas DC e AB, respectivamente. O ponto P, na intersecção da curva da bomba com a curva totalizada
do sistema, é o ponto de operação. Nele temos
Qp = QB + QC (3.9)

34. 3.5.3 Variação da característica do sistema
Ao operar uma bomba em um determinado sistema, a variação de qualquer uma das parcelas da
equação do sistema (3.1) provocará o deslocamento da curva e, consequentemente, do ponto de operação.
De fato, consideremos os seguintes casos:
3.5.3.1 Variação dos níveis dos reservatórios ou das pressões de aspiração e recalque.
Muitas vezes ocorrem variações nos níveis dos reservatórios de sucção e descarga ocorrendo
conseqüentemente variações nas alturas estáticas do sistema. (figura 3.12)
Figura 3.12: Variação no nível do reservatório de sucção
Neste caso, o sistema não será representado por apenas uma curva, e sim por uma faixa de curvas
do sistema compreendida entre as alturas estáticas máxima e mínima.
Para efeito de projeto e selecionamento das bombas, normalmente é considerada a curva do
sistema correspondente ao nível médio ou o nível mais freqüente. É contudo importante o conhecimento
das curvas para os níveis máximo e mínimo principalmente quando ocorrem grandes variações na altura
estática do sistema.
3.5.3.2 Variação da perda de carga ∆H
Afetam a perda de carga ∆H em um determinado sistema:
• o fechamento ou abertura do registro;
• a variação do comprimento das tubulaçòes;
• a variação do diâmetro.
A figura (3.13) mostra o deslocamento sofrido pelo ponto de operação (P), provocado pelo
fechamento do registro (por exemplo). Neste caso, muda na equação do sistema (3.13) o valor de C2 ( a
perda de carga).

35. Figura 3.13: Variação da perda de carga do sistema (registro).
3.6 Dimensionamento de sistemas de bombeamento
A especificação de um sistema de bombeamento é função do conhecimento de duas grandezas
básicas:
- A vazão a ser recalcada (Q) e o tipo de fluido.
- A localização, a diferença de altura e de pressão entre reservatórios de sucção e recalque.
O projeto do sistema envolve uma sequência de operações que pode ser resumida da seguinte
forma:
1) Conhecendo-se a vazão e o fluido a ser bombeado, escolhe-se o material da tubulação e seu
diâmetro, a partir de um dos critérios que veremos a seguir.
2) Conhecendo-se a geometria do sistema, calcula-se então as perdas de carga distribuídas e
localizadas e, com a diferença de altura e pressão entre os reservatórios calcula-se então a altura
manométrica do sistema.
3) Finalmente escolhe-se uma bomba que atenda às características de altura manométrica e vazão
requeridas pelo sistema.
3.6.1 Vazão a ser recalcada
A vazão a ser recalcada por uma bomba em uma instalação depende essencialmente de dois
elementos:
- Consumo diário da instalação;
- Jornada de trabalho;
- Números de bombas em operação (caso das instalações com bombas associadas em paralelo).
O consumo diário da instalação é função da natureza a que se destina a instalação e fim a que se
destina a mesma.
Alguns valores estimados de consumo de água por tipo de instalação são apresentados na tabela
(3.1) a seguir:
Tabela 3.1: Estima de consumo
INSTALAÇÃO CONSUMO litros/dia
residências 150 per capta
apartamentos 200 per capta
hospitais 250 por leito
escritórios 50 per capta
restaurantes 25 por refeição
lavanderia 30 por kg de roupa seca
posto de serviço para automóveis 150 por veículo
fábricas (uso pessoal) por operário
3.6.2 Diâmetros econômicos para uma instalação elevatória

36. Tendo em vista a equação da continuidade em regime permanente para fluidos incompressíveis
(Q = V x A), sabe-se que uma mesma vazão pode ser transportada em tubulações de diferentes diâmetros,
variando a velocidade de escoamento.
A variação do diâmetro, contudo, tem reflexos diretos sobre o investimento e o custo operacional
da instalação, entendendo-se por tais:
- Investimento: dinheiro gasto na aquisição dos tubos;
- Custo operacional: dinheiro gasto para cobrir as despesas com a operação da instalação.
Quanto maior o diâmetro da tubulação, menor será a velocidade e a perda de carga, diminuindo
assim os custos de operação, entretanto, maior será o custo de instalação (custo de um determinado
comprimento de tubulação).
Quando se diminui o diâmetro da tubulação, aumenta-se a velocidade, e assim as perdas de carga,
aumentando-se o custo de operação, mas diminui-se o custo de instalação.
Assim, existe uma solução de compromisso, ou seja, um diâmetro tal que produza o menor custo
total, que é a soma dos custos de investimento e operação.
Baseado neste critério, chamado de Critério do Custo Total Mínimo, existem várias formulas
empíricas que permitem o cálculo do diâmetro econômico para uma instalação.
3.6.2.1 Fórmula de Bresse
D = K. Q (3.10)
onde: D é o diâmetro em m;
K é um coeficiente que é função dos custos de investimento e operação, K varia entre 0,8 a 1,3 (
valor K = 1 é normalmente adotado).
Q é a vazão em m3/s.
A fórmula de Bresse fornece o diâmetro da linha de recalque. Para a linha de sucção adota-se o
diâmetro comercial imediatamente superior.
Quando o diâmetro calculado pela Fórmula de Bresse não coincidir com o diâmetro comercial, é
procedimento usual admitir o diâmetro comercial imediatamente superior para a linha de sucção e o
comercial inferior para a linha de recalque.
3.6.2.2 Fórmula da ABNT
D = 0,586. T1/ 4 . Q (3.11)
onde: D é o diâmetro em m;
T é a jornada de trabalho em horas;
Q é a vazão em m3/s.
Aqui também, não coincidindo o diâmetro calculado com o diâmetro comercial, é procedimento
usual admitir o diâmetro comercial imediatamente superior para a linha de sucção e o imediatamente
inferior para a linha de recalque.
A fórmula da ABNT, frise-se, é usual quando o funcionamento é intermitente.
3.6.3 Velocidade econômica
Em todas as instalações onde o dimensionamento dos diâmetros das linhas de sucção e recalque
obedeceu o critério de conjugar-se o investimento e o custo operacional, de forma a obter-se um custo total
mínimo, constatou-se que as velocidades de escoamento ficaram dentro dos seguintes limites:
Vsucção 1,5 m/s ( no máximo 2,0 m/s);
Vrecalque 2,5 m/s ( no máximo 3,0 m/s).
Assim, o dimensionamento das linhas de sucção e recalque pode basear-se em tais limites de
velocidade, chamadas velocidades econômicas. Usando a equação da continuidade, podemos dizer que :
π. D2
Q = V. A = .V
4
logo,

37. 4.Q
D = (3.12)
π.V
Como valores médios, costuma-se adotar:
Vsucção = 1,0 m/s;
Vrecalque = 2,0 m/s.

38. 20 Lista de exercícios
1. Na figura abaixo, é representado o esquema de um sistema de captação água (T = 26 ºC) de 40m3/h.
O nível do rio, em épocas de seca chegar abaixar até 1,5 metro, por conta disso, trace a curva do
sistema para as vazões : 0, 20, 40, 60 m3/h, com nível de captação de água em -2mt e em -3,5mt.
Material da tubulação e acessórios: aço carbono.
Dados: Patm = 101,3kPa ; Prr = 101,3kPa (abs); Ls = 5,0m; Lr = 100,0m; Hr = 20,0m
2. Um tubo de concreto aço carbono de 125mt de comprimento e 200mm de diâmetro e um tubo de aço
galvanizado de 100mt e 100mm de diâmetro estão ligados em série. Determine o diâmetro de um tubo
equivalente de 225mt, sendo a vazão de 0,1m3/h?
3. Para o sistema de tubos paralelos da figura abaixo, a carga de pressão em A é de 40mca e a carga de
pressão em E é de 32 mca. Supondo que os tubos estejam em um plano horizontal, quais serão as
vazões em cada ramo do anel?
4. Considere as três configurações de sistemas de bombeamento. Desenhe esquematicamente a curva do
sistema de bombeamento, a curva da bomba e mostre o ponto de operação. Para qual configuração a
altura de elevação da bomba é maior que a perda de carga do sistema de bombeamento? E menor? E
igual?
5. Uma quantidade de água (em regime permanente) escoa na razão de 0,05m3/s do reservatório A para
o reservatório B, através de dois tubos de aço ligados em série, como mostra a figura abaixo.
Determine a diferença entre as elevações da superfícies da água nos reservatórios. Despreze todas as
perdas localizadas.

39. Capítulo 4
Hidráulica de Bombas Centrífugas
4.1 Escolha primária das bombas gráficos de seleção
Conhecidos os valores da vazão e da altura manométrica da instalação, para a seleção
preliminar da bomba podemos recorrer aos gráficos que relacionam as faixas de trabalho das
bombas de um fabricante.
Via de regra, o gráfico de seleção consiste de diagramas cartesianos (Hman x Q) dentro dos quais estão
delineados o campo específico de aplicação de cada uma das bombas de uma série de bombas do mesmo
tipo.(apêndice C)
É importante observar que o gráfico de seleção é sempre traçado para uma determinada freqüência da
energia que alimenta o motor a menos de casos especiais, deverão ser consultados, então, os gráficos traçados
para a freqüência de 60Hz, visto ser esta a freqüência padrão do Brasil.
É importante também notar que um mesmo fabricante pode apresentar vários gráficos de seleção. Via
de regra, um gráfico de seleção mostra todo o campo de aplicação de um conjunto de bombas do mesmo tipo
construtivo, porém de tamanhos diferentes. Assim, os gráficos de seleção relativos a um certo fabricante são
tantos quantos os diversos tipos de bombas que constrói.
Em função do exposto, é possível encontrar dentro da linha de produção de um mesmo fabricante, mais
de um tipo de bomba capaz de recalcar a vazão Q na altura manométrica Hman.
A escolha definitiva dependerá da conveniência maior deste ou daquele tipo, retratada através de:
1º Um estudo econômico que compare o custo de compra do conjunto motor e bomba e o seu respectivo custo
operacional (Quanto maior o rendimento, menor será o consumo de energia).
2º Uma adequação entre os materiais empregados na construção da bomba e a natureza do fluído por ela
recalcado. Exemplo que ressalta a importância dessa adequação é o seguinte: é muito comum construir-se a
bomba, executando o rotor em bronze e a carcaça em ferro fundido. Esta combinação de materiais, tão
comum quando o fluído é água doce, é da maior inconveniência quando o fluído é água do mar (salmoura),
isto porque, sendo a salmoura um eletrólito, e o ferro fundido da carcaça é arrancado e depositado sobre o
bronze do rotor, entupindo os canais deste último.
3º Uma adequação entre o tamanho (e até mesmo o peso) da bomba e o espaço disponível da instalação.
Uma adequação entre a capacidade de sucção da bomba especificada e a altura existente na instalação.
No apêndice temos vários gráficos de seleção de bomba para as rotações de 1750 3600rpm.
Exemplo:
Escolha primária de uma bomba centrífuga tipo horizontal para processo, capaz de recalcar uma vazão
(Q) de 20m3/h com uma altura manométrica (Hman) de 30 m.
Resolução:
No gráfico n = 1750 rpm, entramos no eixo das abscissa com a vazão (Q) 20 m3/h e traçamos uma
vertical.
No eixo das ordenadas entramos com a altura manométrica (Hm) 30m, e traçamos uma horizontal.
No cruzamento das linhas da abcissa e das ordenadas temos o tamanho da bomba
escolhida. No nosso caso o tamanho da bomba escolhida é a 40.250.
Nos gráficos de escolha primária de bombas tipo CZ, podemos observar que um mesmo tamanho de
bomba operando a uma rotação de 3500 rpm, é capaz de recalcar com uma mesma vazão (Q), a uma altura
manométrica maior do que se operasse a uma rotação de 1750 rpm.
Isto implica em uma bomba menor, com uma conseqüente diminuição de custo.
Mas na prática, nota-se uma preferência pela bomba operando a uma rotação de 1750 rpm, devido ao
menor nível de ruído, e ao menor desgaste sofrido ao longo do tempo, vindo a compensar o maior investimento
inicial.
4.2 Curvas características das bombas

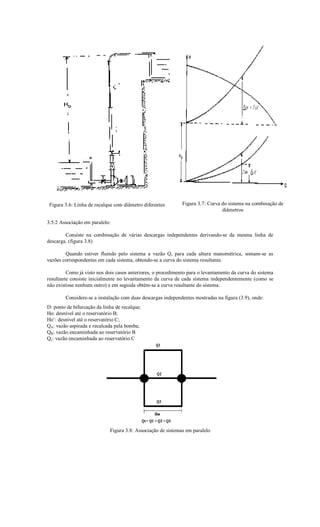
40. Ao se projetar uma bomba, visa-se, especificamente, o recalque de determinada vazão em certa altura
manométrica. Evidentemente, para estas condições, o projeto se desenvolve de modo a obter-se o máximo
rendimento possível para a bomba.
Entretanto, esta bomba poderá, dentro da faixa determinada pela economia, ser posta a recalcar vazões
maiores ou menores que aquela para a qual foi projetada mudando, porém com a variação da vazão os seguintes
elementos:
a) Pressão desenvolvida (Altura manométrica)
Altura manométrica de uma bomba é a energia por unidade de peso que a bomba é capaz de fornecer ao
fluído bombeado e é dada normalmente em metros de coluna de fluído.
b) Potência necessária ao acionamento
Devemos considerar dois tipos de potência:
b.1) Potência hidráulica (Nh)
Representa a potência recebida pelo fluido ao passar pela bomba, que o fará desenvolver a altura
manométrica indicada na vazão determinada. É calculada através da fórmula:
N h = γ × Q × H man (4.1)
onde: Nh = potência hidráulica [W];
γ= peso específico [N/m3];
Q= vazão [m3/s];
Hman = altura manométrica do sistema metros de coluna de fluído [m.c.f.];
b.2) Potência consumida pela bomba (N)
É a potência que a bomba recebe do acionador (motor, turbina).
c) Rendimento da bomba (η)
É a relação entre a potência hidráulica fornecida pela bomba ao fluído e a potência consumida.
N hidraulica N h
η= = (4.2)
N consumida N
onde: Nconsumida é a potência elétrica consumida pelo conjunto motor elétrico-bomba.
Analogamente ao tratamento dispensado à potência hidráulica podemos escrever a seguinte fórmula,
para o cálculo da potência consumida pela bomba (N):
γ × Q × H man
N= (4.3)
η
onde: N = potência consumida pela bomba [W];
γ = peso específico [N/m3];
Q = vazão [m3/s];
Hman = altura manométrica do sistema [m.c.f.];
O rendimento η, é em função do rendimento do motor e da bomba.
η = ηmotor x ηbomba (4.4)
A potência fornecida à bomba pelo motor é:
Nm = Ne x ηm (4.5)
onde: Ne = potência indicada na placa do motor
ηm = rendimento do motor
Nm = potência fornecida à bomba:
A potência hidráulica fica então:
Nh = Nm x ηB (4.6)
onde: Nh = potência hidráulica:
ηB = rendimento da bomba
Logo:

41. Nh = Ne x ηm x ηB (4.7)
Na falta de dados específicos, podem ser tomados os seguintes rendimentos para os motores elétricos
para as bombas centrifugas a 1750 rpm.
Tabela 4.1: Tabela de rendimento de motores em função da potência
N(CV) 1/2 ¾ 1 2 3 5 10 20 30 50 100
ηmotor 64 67 72 75 77 81 84 86 87 88 90
Tabela 4.2: Tabela de rendimento de bombas relativos a vazão
Q(L/s) 5 7 10 15 20 25 30 40 50 100 200
ηbomba 52 61 66 68 71 75 80 84 85 87 88
Por medida de segurança nas especificações de motores recomendam-se os seguintes acréscimos para a
potência instalada:
Tabela 4.3: Acréscimo recomendado
Potência do Motor (CV) até 2 2a5 5 a 10 10 a 20 20
Acréscimo (%) 50 30 20 15 10
As curvas características de uma bomba são diagramas que retratam o seu
funcionamento, mostrando o relacionamento de interdependência existente entre as grandezas
que a caracterizam.
Estas curvas são frutos de experiências do fabricante, que fazem a bomba vencer diversas alturas com
diversas vazões verificando também a potência absorvida e a eficiência da bomba.
As principais curvas características são mostradas na figura (4.1).
- (Hman, Q): retrata a variação da altura manométrica desenvolvida em função da vazão recalcada.
- (η, Q): mostra a variação do rendimento em função da vazão.
- (N, Q): espelha o relacionamento existente entre a potência necessária ao acionamento e a vazão recalcada
- (NPSHreq, Q): variação do NPSH requerido com a vazão.
O aspecto destas curvas depende do tipo de rotor, conforme as figuras (4.1), (4,2) e (4.3)
Figura 4.1: Curvas características de uma bomba radial ou centrífuga pura (rotação de
acionamento constante).

42. Figura 4.2: Curvas características de uma bomba axial (rotação de acionamento constante).
Figura 4.3: Forma comum de apresentação das principais curvas características das bombas pelos fabricantes
(rotação constante).
4.2.1 Curva da altura manométrica (Hman) x vazão (Q):
Esta curva mostra a variação da altura manométrica da bomba com a vazão, mostrada pela equação
(4.8)
ηB  U 2 Qn 
Hm =  − cot gβ 2  (4.8)
∆Pfl  g 60b 2 g




43. onde: Hm: altura manométrica desenvolvida pela bomba, [m];
ηB: rendimento hidráulico da bomba, [%];
∆Pfl: fator de correção;
πd 2n
U2 = : velocidade tangencial do rotor a saída, [m/s];
60
d2: diâmetro externo do rotor, [m];
n: rotação de acionamento, [rpm];
Q: vazão recalcada, [m3/s];
b2: largura do rotor a saída, [m];
β2: ângulo que determina a inclinação da palheta na cauda.
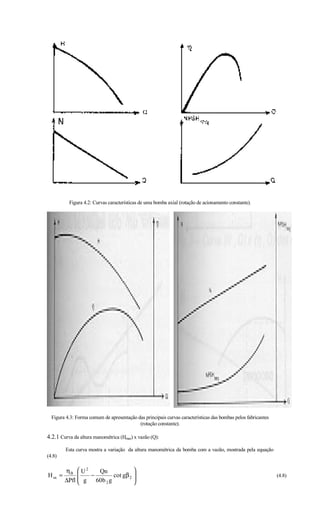
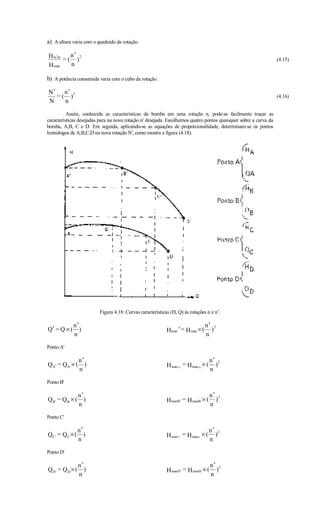
A curva Hman x Q recebe diferentes denominações de acordo com a forma que apresenta, o tipo de curva
esta ligado ao ângulo de inclinação como mostra a figura (4.4):
Figura 4.4: Tipos de curvas características – (Hm x Q)
4.2.1.1 Curva tipo estável
Nesta curva a altura aumenta continuamente com a diminuição da vazão (referente a um rotor estreito com
inclinação de pá = 90º)
Também conhecida como:
Flat no caso de rotor radial;
Rising no caso de rotor diagonal;
Steep no caso de rotor axial
4.2.1.2 Curva tipo instável
Nesta curva a altura manométrica na vazão zero é menor que a desenvolvida para outras vazões (rotor
com inclinação maior que 900). Também conhecidas como Instável e Drooping
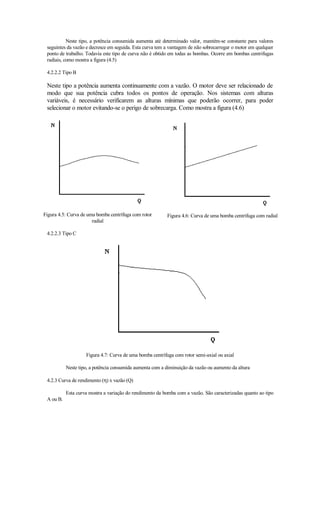
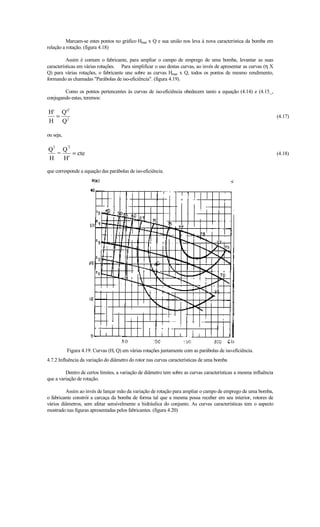
4.2.2 Curva potência consumida (N) x vazão (Q)
Esta curva mostra a variação da potência consumida pela bomba com a vazão. São também de grande
importância e o aspecto físico das mesmas depende do tipo de rotor.
Podem ser do tipo A, B e C
4.2.2.1 Tipo A

44. Neste tipo, a potência consumida aumenta até determinado valor, mantém-se constante para valores
seguintes da vazão e decresce em seguida. Esta curva tem a vantagem de não sobrecarregar o motor em qualquer
ponto de trabalho. Todavia este tipo de curva não é obtido em todas as bombas. Ocorre em bombas centrifugas
radiais, como mostra a figura (4.5)
4.2.2.2 Tipo B
Neste tipo a potência aumenta continuamente com a vazão. O motor deve ser relacionado de
modo que sua potência cubra todos os pontos de operação. Nos sistemas com alturas
variáveis, é necessário verificarem as alturas mínimas que poderão ocorrer, para poder
selecionar o motor evitando-se o perigo de sobrecarga. Como mostra a figura (4.6)
Figura 4.5: Curva de uma bomba centrífuga com rotor Figura 4.6: Curva de uma bomba centrífuga com radial
radial
4.2.2.3 Tipo C
Figura 4.7: Curva de uma bomba centrífuga com rotor semi-axial ou axial
Neste tipo, a potência consumida aumenta com a diminuição da vazão ou aumento da altura
4.2.3 Curva de rendimento (η) x vazão (Q)
Esta curva mostra a variação do rendimento da bomba com a vazão. São caracterizadas quanto ao tipo
A ou B.

45. Figura 4.9: Curva de uma bomba centrífuga com rotor semi-
Figura 4.8: Curva de bomba centrífuga com rotor radial axial ou axial.
4.2.3.1 Tipo A
Este tipo de bomba é a mais indicada quando se deseja variar a vazão, pois o rendimento varia pouco
para larga faixa da mesma.
4.2.3.2 Tipo B
Este tipo de bomba não é a mais indicada quando se deseja variação da vazão.
Da análise do aspecto das curvas características podemos tirar importantes conclusões:
A) A potência necessária ao acionamento cresce com a vazão nas bombas centrífugas com rotor radial e
decresce nas axiais.
Assim para poupar o motor em sua partida, recomenda-se que, para as bombas radiais, o acionamento
seja feito com o registro de recalque fechado: sendo nula a vazão, será miníma a potência necessária ao
acionamento, posteriormente, o registro deverá ser aberto até a vazão de trabalho e assim o motor irá sendo
paulatinamente solicitado.
O contrário acontece com as bombas axiais: para suavizar a partida, esta deverá ser feita com o registro
de recalque totalmente aberto.
B) Nas bombas radiais, o aumento da altura manométrica não produz sobrecarga no motor. Especial
atenção contudo, deve ser dada quando cai a altura manométrica e, conseqüentemente cresce a vazão, pois,
conforme mostra a curva (N x Q) torna-se maior a potência necessária ao acionamento a ponto de sobrecarregar
o motor.
Nas bombas axiais, um raciocínio análogo sobre a curva (N x Q) mostra que a sobrecarga pode
acontecer quando a altura manométrica aumenta e a vazão diminui.
Exemplo:
Deseja-se escolher uma bomba centrífuga radial, fabricante KSB, tipo ETA, operando a uma rotação de
1710 rpm, capaz de recalcar uma vazão de 20m3/h de água, a uma altura manométrica de 30m.
Determinar através das curvas características:
a) modelo
b) diâmetro do rotor
c) rendimento da bomba
d) potência do motor
Resolução:
a) Escolha através dos gráficos de seleção primária:
Pelo gráfico de escolha primária, temos o modelo da bomba:
- CZ 40 - 250
Pelas curvas características da bomba ETA-40-26 temos:
- diâmetro do rotor : 250 mm
- rendimento da bomba : 46 %

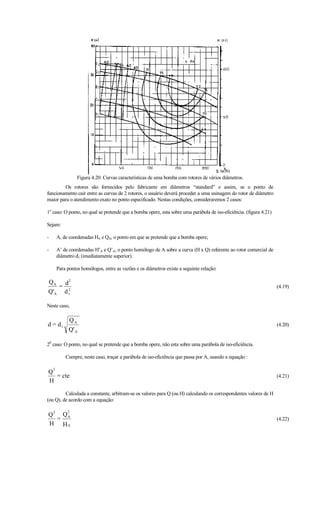
46. - potência do motor : 3,6 CV == 4,0 CV
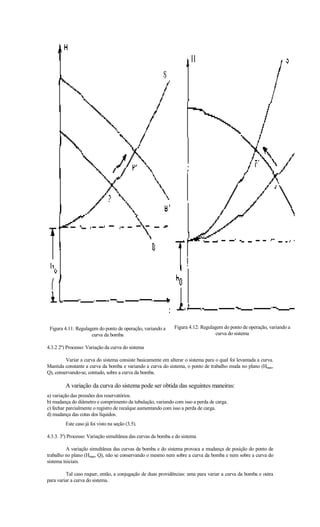
4.3 Ponto de trabalho
Para se obter o ponto de trabalho de uma bomba, deve-se locar a curva do sistema no mesmo gráfico
onde estão as curvas características da bomba.
Na intersecção da curva Q x Hman da bomba com a curva do sistema temos o ponto de trabalho da
bomba.
Assim, levando-se em conta que:
- altura manométrica da bomba: quantidade de energia que 1kg de fluido absorve ao passar pela bomba
(função das dimensões da bomba, da rotação de acionamento e do acabamento interno). É definido pela
equação (4.8):
ηB  U 2 Qn 
Hm = 
 g − 60b g cot gβ 2 
 (4.8)
∆Pfl  2 
onde: Hm: altura manométrica desenvolvida pela bomba, [m];
ηB: rendimento hidráulico da bomba, [%];
∆Pfl: fator de correção;
πd 2 n
U2 = : velocidade tangencial do rotor a saída, [m/s];
60
d2: diâmetro externo do rotor, [m];
n: rotação de acionamento, [rpm];
Q: vazão recalcada, [m3/s];
b2: largura do rotor a saída, [m];
β2: ângulo que determina a inclinação da palheta na cauda.
- Altura manométrica do sistema: quantidade de energia que 1 kg de fluido precisa absorver para vencer o
desnível da instalação, a diferença de pressão entre os dois reservatórios e a perda de carga nas tubulações e
acessórios do sistema. É definida pela equação (3.1)
p rd - prs
H man = Hg + + ∆H (3.1)
γ
onde: Hs = altura de sucção
Hr = altura de recalque
Hg = Hs + Hr (desnível geométrico)
Hm = altura manométrica [m]
prd = pressão no reservatório de descarga [N/m2]
prs = pressão no reservatório de sucção [N/m2]
γ = peso específico [N/m3]
∆H = perda de carga em m.c.f.
ou pode ser escrita como a equação (3.10) no caso de usarmos a perda de carga equivalente
Prd - Prs L Q2
H man = Hg + + 2f 5 (3.10)
ρg D g
e a equação (4.9) no caso de perda de carga localizada
Prd - Prs K 2
H man = Hg + + 5Q (4.9)
ρg D
Ambas as equações podem ser escritas como:
2
H man = C1 + C2 .Q (3.11)
onde os valores de C1 e C2 serão:
Prd - Prs
C 1 = Hg + (3.12)
ρg

47. (H man ,proj − C1) L K
C2 = . = 2f = (3.13)
Q2
proj
5
D g D5
onde K é uma característica que depende do tipo de acessório.
A figura (4.10) mostra a representação gráfica das equações (4.8) e (3.1). A interseção
das duas curvas define o ponto de operação, onde, para a vazão Q, temos a altura manométrica
desenvolvida pela bomba igual à altura manométrica exigida pelo sistema. A partir deste ponto
podemos obter a potência consumida de trabalho e o rendimento de trabalho.
Figura 4.10: Ponto de operação de uma bomba com um sistema
Então a bomba teria como ponto normal de trabalho:
- vazão de trabalho QT
- altura manométrica de trabalho HmanT
- potência consumida de trabalho NT
- rendimento de trabalho ηT
O ponto de trabalho da bomba para o sistema, pode não corresponder com o ponto de
funcionamento ideal da bomba que corresponde ao máximo rendimento.
Existem diversos recursos para modificar o ponto de trabalho e deslocar o ponto de encontro das curvas
Q x Hman da bomba e do sistema. Estes recursos consistem em modificar a curva do sistema ou a curva da bomba,
ou ambas:
Basicamente, deveremos distinguir os seguintes processos de regulagem do ponto de trabalho:
4.3.1. 1º) Processo: Variação da curva da bomba
Mantida constante a curva do sistema e variando a curva da bomba, o ponto de trabalho muda de
posição no plano (Hman, Q), conservando-se, contudo, sobre a curva do sistema.
A variação da curva da bomba pode ser obtida das seguintes maneiras:
a) para o mesmo diâmetro de rotor, mudando a rotação de acionamento.
b) para a mesma rotação de acionamento mudando o diâmetro do rotor.
c) alterar a velocidade.

48. Figura 4.11: Regulagem do ponto de operação, variando a Figura 4.12: Regulagem do ponto de operação, variando a
curva da bomba curva do sistema
4.3.2 2º) Processo: Variação da curva do sistema
Variar a curva do sistema consiste basicamente em alterar o sistema para o qual foi levantada a curva.
Mantida constante a curva da bomba e variando a curva do sistema, o ponto de trabalho muda no plano (Hman,
Q), conservando-se, contudo, sobre a curva da bomba.
A variação da curva do sistema pode ser obtida das seguintes maneiras:
a) variação das pressões dos reservatórios.
b) mudança do diâmetro e comprimento da tubulação, variando com isso a perda de carga.
c) fechar parcialmente o registro de recalque aumentando com isso a perda de carga.
d) mudança das cotas dos líquidos.
Este caso já foi visto na seção (3.5).
4.3.3. 3º) Processo: Variação simultânea das curvas da bomba e do sistema
A variação simultânea das curvas da bomba e do sistema provoca a mudança de posição do ponto de
trabalho no plano (Hman, Q), não se conservando o mesmo nem sobre a curva da bomba e nem sobre a curva do
sistema iniciais.
Tal caso requer, então, a conjugação de duas providências: uma para variar a curva da bomba e outra
para variar a curva do sistema.

49. 4.4 Influência do tempo nas curvas características da bomba e do sistema
Com o tempo, surgem o desgaste e a corrosão e o rendimento da bomba tende a diminuir. Realmente:
- Com a corrosão das paredes e o aparecimento de asperezas, o rendimento hidráulico diminui;
- Com o aumento das folgas e o desgaste dos mancais, o rendimento mecânico cai.
- Com o aumento das folgas há o aumento do vazamento e da recirculação, diminuindo o rendimento
volumétrico.
Figura 4.13: Regulagem do ponto de operação através da variação simultânea das curvas da
bomba e do sistema.
Desta forma, o desgaste e a corrosão
afetam a capacidade da bomba fazendo cair sua
curva (H,Q) no plano.
Mas o tempo, através do desgaste e da corrosão
afetam também a curva do sistema acentuando sua
inclinação, como pode ser observado pela figura
(4.14). Nesta figura as curvas B e S representam as
curvas da bomba e sistema respectivamente quando
novas e as curvas B’ e S’ são as curvas da bomba e
do sistema usados.
4.5 Operação próxima ao ponto de vazão nula
Figura 4.14: Influência do tempo nas curvas da
bomba e do sistema
Os rotores do tipo radial (baixa
velocidade específica) possuem curvas (H x
Q), achatadas, principalmente junto ao
ponto de vazão nula. O emprego deste tipo
de bomba em sistemas, cuja curva (H, Q) é
também achatada, provoca perturbações no
funcionamento devido à proximidade e
imprecisões das interseções das duas curvas
na vizinhança do ponto de vazão nula.
Tal risco, porém, não acontece quando a
curva do sistema é íngreme. Especial
cuidado deve0se também Ter, na operação
Figura 4.15: Operação próxima ao ponto de vazão na vizinhança do ponto de vazão nula, com
nula. o motor de acionamento, quando a bomba
é do tipo axial

50. Tal cuidado decorre do fato de, sendo a
curva (N, Q) da potência necessária ao
acionamento descendente, de se exigir do
motor uma potência (N) bem maior que aquela
para a qual foi dimensionada (Np), provocando
sobrecarga. (Tal fato ocorre quando, para
atendimento da demanda, fecha-se o registro
em instalações com bombas axiais).
4.6 Bancada de ensaios de bombas
Uma bancada de ensaios de bombas é uma
instalação que permite o levantamento das
curvas características das mesmas.
Podem divergir em termos dos equipamentos e
acessórios usados para se fazer as medições, dada a
grande variedade destes. Basicamente, é constituída por
um circuito hidráulico fechado onde, além da bomba a
testar e da fonte de acionamento, comparecem os
seguintes aparelhos e equipamentos:
- Aparelho para regulagem e medição da vazão;
Figura 4.16: A potência N (próxima à vazão nula)
é maior que a potência Np de projeto (bombas
axiais)
- Aparelhos para medição da potência necessária ao acionamento;
- Aparelhos para medição do rendimento;
- Aparelho para medição da rotação de acionamento;
- Equipamento para fazer variar a rotação de acionamento da bomba.
Figura 4.16: Esquema de uma bancada de ensaios de bombas

51. Figura 4.17: Medição da potência no eixo.
4.6.1 Medição da altura manométrica da bomba.
Como se mostrou anteriormente, podemos fazer a medição direta da altura manométrica, através de
manômetros.
- Bombas de sucção positiva
pd + ps
Hman = + Zds (3.4)
γ
- Bombas de sucção negativa
pd
Hman = − ( H gs − Zds ) (3.5)
γ
Para as medições usam-se manômetros metálicos ou, quando desejar uma maior precisão, os
manômetros de peso morto.
4.6.2 Regulagem e medição da vazão
A regulagem é feita através do registro de recalque e, na medição da vazão, podem ser usados:
- Vertedores;
- Venturímetros;
- Placas de orifício;
- Rotâmetros;
- Caixa de taragem (processo direto).
4.6.3 Medição da potência necessária ao acionamento
Para tal são normalmente usados, no acionamento das bombas, os motores dinamométricos de carcaça
pendular. (figura 4.17)
O princípio básico da medição consiste em, estando solta a carcaça do motor, este
tende, pela reação, a girar no sentido contrário do giro do rotor do motor. Esse movimento da
carcaça é, no entanto, sustado por um prato de balança, sobre o qual vem apoiar um pino preso
a um braço de alavanca solidário à carcaça do motor. Atingindo o equilíbrio dinâmico, a força
F transmitida pelo pino ao prato da balança é, evidentemente, o peso lido no mostrador da
mesma. Pode-se então, para cálculo da potência necessária ao acionamento, fazer uso do
seguinte formulário:
N = M⋅ω (4.10)
onde: M: momento de torção;

52. ω: velocidade angular.
Como:
πn
M = F× R e ω=
30
Teremos:
πr
N= F⋅n (4.11)
30
A rotação n no eixo do motor é medida com um conta-giros (tacômetro) ou com um estroboscópio.
4.6.4 Medição do rendimento da bomba
O rendimento de uma bomba pode ser definido como sendo a relação entre a potência absorvida pelo
jato líquido e a potência no eixo da bomba.
Assim, como:
N jato = γ.Q.H man (4.12)
e
πr
N eixo = F⋅n (4.11)
30
Teremos:
N jato 30γ.Q.H man
η= = (4.13)
N eixo πRF.n
4.6.5 Medição da rotação
Pode ser feita através de conta-giros, tacômetro e com um estroboscópio.
4.6.6 Variação da rotação de acionamento
Esta variação da rotação é necessária para obter as curvas características de uma mesma bomba em
diferentes rotações de acionamento.
Podem ser usados:
- Um motor elétrico de corrente contínua, onde a variação de rotação é obtida no próprio reostato do motor.
Sendo alternada a corrente de alimentação, exige-se uma fonte retificadora de corrente.
Um motor elétrico de corrente alternada acoplado a um variador mecânico de velocidade.
Outros equipamento podem ser usados, sem, contudo, oferecer a mesma economia, segurança e comodidade
operacional inerentes aos motores elétricos, sejam de corrente alternada ou contínua.
4.7 Leis de similaridade
4.7.1-Influência da rotação nas curvas características da uma bomba
Existe uma proporcionalidade entre os valores Q, Hman e N com a rotação, assim sendo, variando a
rotação de acionamento, muda a curva característica da bomba.
A cada ponto Hman x Q da curva da bomba a uma rotação n corresponde, em semelhança mecânica a
um outro ponto Hman x Q' sob rotação n', tal que:
a) A vazão é proporcional à rotação:
Q′ n ′
= (4.14)
Q n

53. a) A altura varia com o quadrado da rotação.
H m′an n′ 2
=( ) (4.15)
H man n
b) A potência consumida varia com o cubo da rotação.
N′ n′
= ( )3 (4.16)
N n
Assim, conhecida as características da bomba em uma rotação n, pode-se facilmente traçar as
características desejadas para na nova rotação n' desejada. Escolhemos quatro pontos quaisquer sobre a curva da
bomba, A,B, C e D. Em seguida, aplicando-se as equações de proporcionalidade, determinam-se os pontos
homólogos de A,B,C,D na nova rotação N', como mostra a figura (4.18).
Figura 4.18: Curvas características (H, Q) às rotações n e n’.
n′ n′ 2
Q′ = Q × ( ) H man ' = H man × ( )
n n
Ponto A'
n′ n′ 2
QA′ = QA × ( ) H man A′ = H man A × ( )
n n
Ponto B'
n′ n′ 2
Q B′ = Q B × ( ) H manB′ = H manB × ( )
n n
Ponto C'
n′ n′ 2
QC ' = QC × ( ) H man C ′ = H man C × ( )
n n
Ponto D'
n′ n′ 2
QD' = QD × ( ) H manD′ = H manD × ( )
n n

54. Marcam-se estes pontos no gráfico Hman x Q e sua união nos leva à nova característica da bomba em
relação a rotação. (figura 4.18)
Assim é comum o fabricante, para ampliar o campo de emprego de uma bomba, levantar as suas
características em várias rotações. Para simplificar o uso destas curvas, ao invés de apresentar as curvas (η X
Q) para várias rotações, o fabricante une sobre as curvas Hman x Q, todos os pontos de mesmo rendimento,
formando as chamadas Parábolas de iso-eficiência. (figura 4.19).
Como os pontos pertencentes às curvas de iso-eficiência obedecem tanto a equação (4.14) e (4.15_,
conjugando estas, teremos:
H' Q'2
= (4.17)
H Q2
ou seja,
2 '2
Q Q
= = cte (4.18)
H H'
que corresponde a equação das parábolas de iso-eficiência.
Figura 4.19: Curvas (H, Q) em várias rotações juntamente com as parábolas de iso-eficiência.
4.7.2 Influência da variação do diâmetro do rotor nas curvas características de uma bomba
Dentro de certos limites, a variação de diâmetro tem sobre as curvas características a mesma influência
que a variação de rotação.
Assim ao invés de lançar mão da variação de rotação para ampliar o campo de emprego de uma bomba,
o fabricante constrói a carcaça da bomba de forma tal que a mesma possa receber em seu interior, rotores de
vários diâmetros, sem afetar sensivelmente a hidráulica do conjunto. As curvas características tem o aspecto
mostrado nas figuras apresentadas pelos fabricantes. (figura 4.20)

55. Figura 4.20: Curvas características de uma bomba com rotores de vários diâmetros.
Os rotores são fornecidos pelo fabricante em diâmetros “standard” e assim, se o ponto de
funcionamento cair entre as curvas de 2 rotores, o usuário deverá proceder a uma usinagem do rotor de diâmetro
maior para o atendimento exato no ponto especificado. Nestas condições, consideraremos 2 casos:
1o caso: O ponto, no qual se pretende que a bomba opere, esta sobre uma parábola de iso-eficiência. (figura 4.21)
Sejam:
- A, de coordenadas HA e QA, o ponto em que se pretende que a bomba opere;
- A’ de coordenadas H’A e Q’A, o ponto homólogo de A sobre a curva (H x Q) referente ao rotor comercial de
diâmetro d1 (imediatamente superior).
Para pontos homólogos, entre as vazões e os diâmetros existe a seguinte relação:
QA d2
= 2 (4.19)
Q'A d 1
Neste caso,
QA
d = d1 (4.20)
Q' A
20 caso: O ponto, no qual se pretende que a bomba opere, não esta sobre uma parábola de iso-eficiência.
Cumpre, neste caso, traçar a parábola de iso-eficiência que passa por A, usando a equação :
2
Q
= cte (4.21)
H
Calculada a constante, arbitram-se os valores para Q (ou H) calculando os correspondentes valores de H
(ou Q), de acordo com a equação:
2 2
Q Q
= A (4.22)
H HA

56. Figura 4.21: O ponto A esta sobre uma curva de iso-eficiência
Traçada a curva dos pontos homólogos, tem-se (graficamente) na interseção desta com a curva (H, Q)
relativa ao rotor de diâmetro d1, o ponto A' de coordenadas H'A e Q'A (homólogo de A).
Aqui novamente:
QA d2
= 2 (4.19)
Q'A d 1
Neste caso,
QA
d = d1 (4.20)
Q' A
Obs: Na usinagem do rotor, a variação do raio final não deve ser maior que 10%.
4.7.3 Influência do peso específico (γ) nas curvas características de uma bomba
Imaginemos duas bombas iguais, funcionando com o mesmo número de rotações por minuto, mas com
líquidos de pesos específicos diferentes.
Se a viscosidade em ambos os casos for a mesma, a experiência tem mostrado que:
a) o rendimento se mantêm praticamente o mesmo nos dois casos;
b) as alturas manométricas geradas pelo rotor são as mesmas, porque as velocidades tanto do rotor como
do líquido não mudam.
c) as alturas representativas das pressões variarão, porque a pressão é proporcional ao peso específico do
fluído.
p= γ*H (4.23)
Sabemos que a altura manométrica é:
p rd - p rs
H man = H g + + ∆H (4.24) Sab
γ
Resta o termo (prd - prs)/γ a considerar.

57. Quando γ aumenta para γ', a altura manométrica continua a mesma. Para que a fração não mude (pois
senão mudaria a altura monométrica), deveremos aumentar o numerador (prd - prs) na mesma proporção em que
γ aumenta isto é:
prd - prs p r′d - pr′s
= (4.25)
γ γ′
Portanto, a variação de pressão entre a saída e a entrada do rotor serão tanto maior, quanto maior for o
peso específico.
Uma bomba que trabalhasse com líquido de maior pêso específico acusaria maiores pressões no
manômetro da boca de saída da bomba, embora levasse o líquido à mesma altura estática.
A potência motriz variará diretamente com o peso específico porque:
γ × Q × H man
N= (4.26)
η
Admitamos que o líquido (por exemplo, a água) se ache na temperatura normal (15ºC). Se a água for
quente seu peso específico será menor.
Nas bombas de água quente para caldeiras, a redução do pêso específico pode ser de 15% ou mais. É
preciso continuar a bombear um dado pêso de água por segundo (não um dado volume, porque o que se deseja na
caldeira é massa de vapor por unidade de tempo) contra uma pressão estipulada, que aumenta na caldeira com o
aumento de temperatura. Assim a potência consumida para acionar a bomba aumentará com o aumento da
temperatura da água.
4.8 Velocidade específica
Na classificação das bombas centrifugas, vimos que existem vários tipos e fizemos uma escolha
preliminar baseada na vazão (Q) e na altura manométrica (Hm).
Estudaremos agora um critério para escolhermos a bomba centrífuga, quando forem fixadas a vazão
(Q), a altura manométrica (Hm) e a rotação (n).
Este critério de escolha da bomba é através da velocidade específica. Esta velocidade específica é assim
definida:
Velocidade específica (ns) é a rotação na qual deverá operar a bomba para recalcar a vazão de 1m3/s em uma
instalação com 1m de altura manométrica, com o máximo rendimento.
É conhecido que bombas geométricamente semelhantes são teoricamente semelhantes. Assim sendo,
bombas geométricamente similares possuem curvas características similares.
Para propiciar uma base de comparação entre os vários tipos de bombas desenvolveu-se um fator que
relaciona os três dos principais fatores característicos do funcionamento:
vazão
altura manométrica
rotação
Este fator é a velocidade específica.
A velocidade específica é um número adimensional expresso matematicamente através da seguinte
fórmula:
n Q
ns = 4 3
(4.27)
H m
onde: ns = velocidade específica;
Q = vazão em m3/s;
Hm = altura manométrica em metros;
n = rotação (rpm);
Observações:
1ª) Em bombas com rotor de dupla sucção dividir a vazão por 2 para entrar na fórmula;.

58. 2ª) Para bombas de multi-estágio, dividir a altura manométrica (Hm) pelo número de estágios;
Todas as bombas geométricamente semelhantes entre si terão uma só velocidade específica a qual as
caracterizará. A importância da determinação da velocidade resulta de que a mesma fornece um termo de
comparação entre as diversas bombas sob o ponto de vista da velocidade e de ser o seu valor decisivo na
determinação do formato do rotor a empregar para atender a um número de rotações n, a uma descarga Q e uma
altura manométrica Hm.
Assim o valor ns especifica o tipo de bomba centrifuga a empregar. Baseados nos resultados obtidos
com bombas ensaiadas e no seu custo, o qual depende das dimensões das bombas, os fabricantes elaboraram
tabelas, gráficos e ábacos delimitando o campo de emprego de cada tipo conforme a velocidade específica, de
modo a proceder a uma escolha que atenda as exigências de bom rendimento e baixo custo.
Assim, segundo esse critério, podemos classificar as bombas centrífugas em:
a) Lentas: ns 90 bombas centrífugas puras, com pás cilíndricas radiais, para pequenas e médias descargas.
b) Normais: 90 ns 130 bombas semelhantes às anteriores.
c) Rápidas: 130 ns 220 possuem pás de dupla curvatura; descargas médias.
d) Extra-rápidas ou hélico centrifugas: 220 ns 440 possuem pás de dupla curvatura; descargas médias e
grandes.
e) Helicoidais: 440 ns 500 para descargas grandes.
f) Axiais: ns 500 assemelham-se a hélices de propulsão. Destinam-se a grandes descargas e pequenas alturas
de elevação.
Observações:
1ª) As bombas centrífugas de maiores valores de velocidade específica correspondem às de menores dimensões.
2ª) A caracterização do tipo do rotor depende não apenas de Q e Hman, mas também de n.

59. Capítulo 5
Associação de Bombas
Em estações elevatórias de água ou esgotos e em inúmeras aplicações industriais, o
campo de variação da vazão e da altura manométrica pode ser excessivamente amplo, para ser
atendido por uma única bomba, mesmo variando a velocidade. Recorre-se então à associação
ou ligação de duas ou mais bombas em série, ou em paralelo.
Figura 5.1: Esquema típicos de associação em paralelo e em série
A associação em paralelo comparece com frequência no abastecimento de água de cidades, bem como
em serviços industriais e tem a finalidade de aumentar a vazão recalcada e dar ao sistema uma maior
flexibilidade em termos de atendimento da demanda, através da retirada ou colocação das unidades em
funcionamento.
Esta retirada de unidades em funcionamento para atendimento da demanda permitirá, inclusive, a
existência de uma manutenção preventiva (programada até) de reflexos altamente positivos.
A associação em série é, por sua vez, o arranjo que resolve o problema de instalações de alturas
relativamente elevadas, quando se torna, então, necessário o desenvolvimento de grandes pressões.
Figura 5.2: Bomba de dupla sucção
Figura 5.3: Bomba multicelular
Tanto a associação em paralelo como a associação em série podem se processar através do emprego de
unidades independentes ou através da associação, seja em paralelo ou em série, de rotores dentro de uma única
carcaça.
No caso da associação em paralelo, teremos a bomba de dupla sucção (justaposição de dois rotores pelo
costado), com a vantagem do equilíbrio dos empuxos axiais (obtido através da equalização das pressões de
sucção e descarga, de um lado e outro do rotor). (figura (5.2)

60. No caso de associação em série teremos a bomba multicelular (bomba de vários estágios), com a
vantagem de eliminar a multiplicação das casas de bombas e de unificar as unidades de acionamento e controle,
propiciando melhor rendimentos e custos mais baixos.
5.1 Associação de bombas em série
A associação de bombas em série é o arranjo que resolve o problema de instalações de alturas
manométricas relativamente altas quando se torna, então, necessário o desenvolvimento de grandes pressões.
Um conjunto constituído de duas ou mais bombas em série terá altura manométrica igual à soma das
alturas manométricas de cada bomba, admitindo-se a mesma vazão.
Para se obter a curva característica resultante da associação de duas bombas, sejam elas iguais ou
diferentes, basta somar para cada valor da vazão, as alturas manométricas correspondente a ambas as bombas.
Assim, para a vazão Qt, temos:
H = H1 + H 2 (5.1)
Um exemplo comum de bombas operando em série é o das bombas de vários estágios. Tudo se passa
como se cada estágio fosse uma bomba isolada. A vazão é a mesma em cada estágio e as alturas manométricas
vão se somando às anteriores.
Observar que a associação de rotores em série numa mesma carcaça apresenta, sobre a associação em
série de bombas, a vantagem da não multiplicação de casas de bombas, dos órgãos de acionamento e dos órgãos
de comando e controle de operação.
Na associação de bombas em série, observar se a flange de sucção da Segunda agüenta a pressão de
descarga da primeira e ainda as a carcaça da Segunda suporta a pressão de descarga total.
Figura 5.4: Esquema de ligação de bombas em série e mudança do ponto de operação para duas bombas
idênticas
5.2 Associação de bombas em paralelo
Consiste na ligação da tubulação de recalque de cada bomba em uma tubulação em comum, de modo
que cada bomba contribua com uma parcela da vazão total.
A favor de associação de bombas independentes em paralelo, deve-se realçar pesa a flexibilidade do
sistema em termos de se poder varias a vazão para atendimento do consumo através do desligamento de uma ou
mais unidades, (o que pode permitir, inclusive, a manutenção das unidades que não estejam em funcionamento).

61. Figura 5.5: Associação em série de duas bombas diferentes
Um conjunto constituído de bombas em paralelo terá mesma altura manométrica de cada bomba e
vazão igual à soma das vazões de cada bomba desde que não seja alterada a altura manométrica. (figura 5.6)
Figura 5.6: Curva resultante da associação de duas bombas idênticas em paralelo
5.2.1 Associação em paralelo de bombas iguais com curvas estáveis
É o caso mais recomendado e comum na associação em paralelo. Para a obtenção da curva de duas
bombas iguais associadas em paralelo, basta marcar o dobro da vazão para cada bomba. (figura 5.6)
Quando as duas bombas estão operando, a vazão no sistema é Q2 e cada bomba recalca uma vazão Q1 ,
de tal forma que Q2 = 2 x Q1.
Note-se que as duas bombas operarão com a mesma altura manométrica.
Quando uma bomba só opera, a altura manométrica total diminuí, passando para Hman1' , e para uma
vazão Q1'.

62. Figura 5.7: Curva resultante da associação de duas bombas idênticas em paralelo
A figura (5.7) mostra este mesmo caso e observando-a pode-se tirar as seguintes conclusões:
a) Posta a operar isoladamente no sistema, a bomba recalca uma vazão maior do que quando associada em
paralelo (Q’QA) e requer uma potência de acionamento maior, o que implica na necessidade de escolha de
um motor capaz do atendimento desse ponto (caso de bombas radiais0.
b) Igualmente importante é observar que o NPSH requerido na operação isolada é maior que o NPSH
requerido quando do funcionamento em paralelo (NPSH’r NPSHr). Assim, se o NPSH requerido, na
operação isolada, passar a ser maior que o NPSH disponível no sistema, a bomba entrará em regime de
cavitação.
c) Quando as bombas estão operando em paralelo, há um deslocamento do ponto de operação para a direita da
curva.
5.2.2 Associação em paralelo de bombas iguais com altura estática variável
É o caso mostrado na figura (5.8)
Figura 5.8: Associação em paralelo de bombas iguais com altura estática variável.
Em tal circunstância, deveremos destacar que:
- P1 e P2: Pontos de funcionamento para uma única bomba funcionando com o nível mínimo e máximo
do poço, respectivamente.
Tais pontos localizam-se, na interseção da curva da bomba (isolada) com as curvas características do
sistemas referentes as níveis de mínimo e máximo respectivamente.

63. Isto porque, a variação de nível provoca a translação da curva do sistema no plano cartesiano (na
equação (3.1) o que muda é Hg).
Especial atenção dever-se-á dar ao ponto P2 (ponto de funcionamento de uma bomba com o nível
máximo), de vez que em tal situação:
1. É requerido o máximo de NPSH pela bomba, situação na qual, dependendo do valor de NPSH
disponível, poderá haver cavitação (quando NPSH req NPSH disp)
2. Exige-se o máximo de potência do motor de acionamento (caso de bombas radiais).
3. O rendimento poderá cair excessivamente.
- P3 e P4: Pontos de funcionamento para as duas bombas associadas em paralelo com os níveis de
máximo e mínimo do poço, respectivamente:
Nestas condições:
1. Quando o nível do poço for máximo, P6 definirá as coordenadas de funcionamento por bomba (ambas
associadas em paralelo).
2. Quando o nível do poço for mínimo, P5 definirá as coordenadas de funcionamento por bomba (ambas
associadas em paralelo).
Neste caso, se as bombas forem do tipo axial (curva (N,Q) decrescente) e se estiverem trabalhando
com vazão pequena, o motor poderá estar sendo solicitado em potência tal que provoque o
sobreaquecimento (curva (N,Q) descendente).
5.2.3 Associação em paralelo de bombas diferentes com curvas estáveis
A associação em paralelo de bombas diferentes com curvas estáveis é viável, devendo, contudo e
sempre que possível, ser evitada, pelos muitos problemas que podem aparecer.
Sejam B1 e B2 (figura 5.9) as curvas características de duas bombas diferentes que deverão ser
postas a trabalhar em paralelo nos sistemas S1 e S2, respectivamente
Figura 5.9: Associação em paralelo de bombas diferentes com curvas estáveis.
1o caso: Associação em paralelo no sistema S1. É o caso viável da associação em paralelo de bombas
diferentes com curvas estáveis. Neste caso:
- Funcionando apenas a bomba B1: a vazão recalcada será Q1 e a altura manométrica desenvolvida será
H1.
- Funcionando apenas a bomba B2: a vazão recalcada será Q2 e a altura manométrica desenvolvida será
H2.
- Funcionando B1 em paralelo com B2: a vazão recalcada será Qt e a altura manométrica desenvolvida
será Ht.: Note que:
Q t = Q'1 + Q'2 (5.2)
onde: Q'1 : a vazão recalcada pela bomba B1
Q' 2 : a vazão recalcada pela bomba B2
2o caso: Associação em paralelo no sistema S2. Se a altura manométrica a ser desenvolvida for maior ou
igual a Hc, a bomba B1 estará operando com vazão nula (Q1 = 0), não tendo, assim, sentido a associação
em paralelo.
5.2.4 Associação em paralelo de bombas iguais com curvas instáveis
Sejam duas bombas iguais B1 e B2 que deverão ser postas a operar em paralelo nos sistemas S1 e
S2 (note-se que as bombas possuem curvas instáveis, caracterizadas pelo ramo ascendente na origem).
(figura 5.10)

64. Figura 5.10: Associação em paralelo de bombas iguais com curvas instáveis.
Trata-se de uma associação em paralelo pouco recomendada pelos inconvenientes funcionais que
apresenta, principalmente quando o sistema for S1.
Realmente, ligando-se a primeira bomba no sistema S1, ela irá recalcar a vazão Q1 e desenvolver
a altura manométrica H1, que atuará sobre a válvula de retenção da Segunda bomba. Assim, dada a partida
na Segunda, tudo se passará como se esta estivesse partindo com o registro fechado, desenvolvendo uma
pressão HH1, e portanto, não descarregando no sistema.
Desta forma, apresenta-se problemática e colocação da segunda unidade em funcionamento, o que
só ocorre normalmente quando a altura total desenvolvida (na associação) for menor que a altura
correspondente à vazão nula de uma única bomba (caso do sistema S2, quando H2H1),

65. 3a Lista de Exercícios
1. Um sistema de bombeamento de água está configurado como mostra o esquema abaixo. Se a curva
característica da bomba é dada, determinar o ponto de operação do sistema e a vazão para cada
reservatório de recalque. As perdas de carga nos trechos que constituem o sistema são:
4 5
10 m
2
1
3
3m
Zs = 0.01 Q2 , Z2-3 = 0.035 Q2, Z3-4 = 0.1 Q2, Z3-5 = 0.3 Q2,
se Z ≡ (mca) e Q ≡ (m3/h).
5 0 .0 0
4 5 .0 0
52
A ltu ra M an. H (m )
η (−)
4 0 .0 0
48
3 5 .0 0
3 0 .0 0
5 .0 0 10.00 1 5 .0 0 2 0 .0 0 2 5 .0 0
V azão (m 3 /h)
2. No sistema de bombeamento do problema anterior, considere a instalação de duas bombas
semelhantes em série (curva fornecida abaixo). Determine o novo ponto de operação do sistema e o
ponto de operação de cada uma das bombas individualmente (H, Q, η, e N). Determine também a
vazão para cada reservatório.
35 .00 56
54
30 .00
A ltu ra M a n . H (m )
52
η (−)
25 .00
50
20 .00
48
15 .00 46
10 .00 1 5.00 2 0.00 2 5.00 3 0.0 0
V a zã o (m 3 /h )

66. Capítulo 6
Cavitação e NPSH
6.1 Pressão de vapor
Para um perfeito entendimento do conceito de cavitação e NPSH (NEAT POSITIVE SUCTION
HEAD) é necessário rever o conceito de pressão de vapor.
Pressão de vapor de um líquido a uma dada temperatura é aquela na qual o líquido coexiste em sua
fase líquida e vapor.
Nessa mesma temperatura, quando tivermos uma pressão maior que a pressão de vapor, haverá
somente a fase líquida e quando tivermos uma pressão menor, somente a fase vapor.
A pressão de vapor de um líquido cresce com o aumento da temperatura. Assim, caso a temperatura
seja elevada até um ponto em que a pressão de vapor iguale por exemplo a pressão atmosférica, resultará na
evaporação do líquido, ocorrendo o fenômeno da ebulição.
No apêndice (A1) apresentamos uma tabela com a pressão de vapor da água para várias temperaturas.
6.2 Altura de colocação de uma bomba
Quanto à posição da bomba em relação ao nível de água do poço de sucção podemos ter:
- Bombas com sucção positiva
- Bombas com sucção negativa ou bombas afogadas
Sucção positiva Sucção negativa
Figura 6.1: Bombas em relação a altura de sucção
Raciocinando com a figura (6.1) e aplicando a equação de Bernoulli entre o nível de água de captação
(grandezas referidas pelo índice 0) e a entrada da bomba (grandezas definidas pelo índice 1), podemos escrever:
2 2
p0 v 0 p1 v1
+ =− + + HA + ∆H0→1 (6.1)
γ 2g γ 2g
Assim, a coluna de líquido equilibrada pela bomba em sua sucção é dada por:
p −p v2 − v2
HA = a 1 − 1 0 − ∆H
A (6.2)
γ 2g
onde, para simplificar a notação, torna-se:
p0 = pa pressão atmosférica;
∆H0→1 = ∆HA perda de carga na linha de sucção
Considerando condições ideais de funcionamento para a bomba, ou seja, desprezando a variação da
energia cinética e a perda de carga na sucção:
v2 − v2
1 0 = 0 ∆H = 0
A
2g
Teremos:
p − p1
HA = a (6.3)
γ

67. Assim, a máxima altura de líquido equilibrada por uma bomba ocorre quando se tem a pressão p1 ,
nula, ou seja, quando se criasse o vácuo absoluto à entrada da bomba. Nestas condições, para uma bomba
operando água fria ao nível do mar:
p 101325Pa
HAmax = a = = 10,1325mca
γ 1000N / m3
Na prática, contudo, a maior coluna de liquido equilibrada pela bomba em sua sucção é menor que
10,315 m ( aproximadamente 7,5 m, dependendo do tipo de bomba). Isto porque:
- Não são desprezíveis a perda de carga na sucção e a variação da energia cinética
- Na tentativa de reduzir a pressão à entrada da bomba a seu valor mínimo, tão logo atingirmos a pressão de
vapor de líquido à temperatura de bombeamento, inicia-se o aparecimento da cavitação com prejuízo para o
normal funcionamento da bomba.
6.3 Cavitação
Na sucção das bombas centrífugas, ocorrem inevitavelmente rarefações do líquido, isto é, pressões
reduzidas devidas à própria natureza do escoamento ou ao movimento impresso pelas peças móveis ao líquido.
Caso esta pressão atingir a pressão de vapor do líquido na temperatura em que este se encontra, haverá
uma intensa formação de vapor.
Inicialmente, nas regiões mais rarefeitas formam-se pequenas bolsas, bolhas ou cavidades (daí o nome
de cavitação) no interior das quais o líquido se vaporiza. Em seguida, conduzidas pela corrente líquida provocada
pelo movimento do rotor e com grande velocidade, atingem pressões mais elevadas onde ocorre a implosão
(colapso) destas bolhas com a condensação do vapor e o retorno ao estado líquido. Tal fenômeno é conhecido
como cavitação.
Com a condensação das bolhas, a água circundante acelera-se no sentido centrípeto. Com o
desaparecimento da bolha, ou seja, com a sua condensação, as partículas aceleradas se chocam cortando umas o
fluxo das outras.
Ocorre desta forma um golpe de aríete e com ele uma sobrepressão contrária que se propaga em todas
as direções, golpeando, através de fortíssimos choques, as paredes e palhetas mais próximas.
Os efeitos da cavitação são visíveis, mensuráveis e até audíveis, com ruído característico similar a um
misturador de concreto.
Figura 6.2: Corte do fluxo de líquido bombeado, quando pi pe (pe = pressão da seção pressão de
vapor)
Tabela 6.1: Cavitação (Efeito mecânico)

68. Além de provocar corrosão, desgastando, removendo partículas e destruindo pedaços dos rotores e dos
tubos de aspiração junto à entrada da bomba, a cavitação se apresenta produzindo:
- queda de rendimento da bomba
- marcha irregular, trepidação e vibração da máquina, pelo desbalanceamento que acarreta
- ruído, provocado pelo fenômeno de implosão
As figura seguintes são do Institut de Machine Hydraulique et de Méchanique des Fluides,
França (cavitação no perfil 2D NACA e nas pás de rotor de bomba), e do Naval Architecture and Ocean
Engineering da University of Tokyo, Japão (foto ampliada de cavitação “em nuvem”, cloud cavitation, em
um perfil hidrodinâmico), ilustrando a cavitação ocorrendo em dispositivos variados (material retirado da
apostila da UNICAMP)
Figura 6.3: Cavitação em
Venturi, ENLP, França Figura 6.4: Cavitação em perfil 2D NACA (IMHMF, França)

69. Figura 6.5: Cavitação em rotor de bomba e região erodida (IMHMF, França)
Desta forma, a cavitação age como um fator limitativo da altura de colocação da bomba, fazendo com
que o máximo valor desta (Hamax) ocorra quando p1 = p v , onde pv é a pressão de vapor do fluido na temperatura
de bombeamento.
Podemos escrever, então:
2 2
p − p v v1 − v0
HAmax = a − − ∆HA (6.4)
γ 2g
6.4 Materiais a serem empregados para resistir à cavitação
A escolha do material a ser utilizado na fabricação da bomba é de muita importância. Alguns materiais
na ordem crescente de sua capacidade de resistir a corrosão por cavitação são: ferro fundido, alumínio, bronze,
aço fundido, aço doce laminado, bronze fosforoso, bronze manganês, aço níquel, aço cromo (Cr +2) e ligas de aço
inoxidável especiais.
A rigor não há nenhum material conhecido que não seja afetado pela cavitação.
A resistência de materiais à corrosão por cavitação é determinada em ensaios de laboratório, quando os
corpos de prova, pesados inicialmente são colocados num difusor onde se medem a pressão e a velocidade da
água (por exemplo pressão de 50 kgf/cm2 e velocidade de 100m/s). Decorrido certo tempo (digamos 150 horas),
mede-se a perda de material por diferença na pesagem do corpo de prova. Esta perda define a resistência ao
desgaste por cavitação.
Recentemente tem-se empregado revestimento com elastômeros, que demonstram grande resistência à
cavitação. Como por exemplo do neoprene, poliuretano, estireno butadieno e de outros elastômeros. Os dois
primeiros podem ser aplicados sob a forma líquida e apresentando grande aderência ao metal (C.P. Kittredge.
Centrifuga Pump Performance. McGraw-Hill).
6.5 Medidas destinadas a dificultar o aparecimento da cavitação
Os fabricantes de bombas, com sua experiência adquirida ao longo do tempo, já tomam, várias medidas
no projeto e fabricação da bomba para dificultar o aparecimento da cavitação, ficando portanto, as
recomendações destinadas apenas ao usuário da bomba, durante a instalação da mesma.
Figura 6.6: Poços de sucção com turbulências. Soluções possíveis

70. As principais medidas a serem tomadas por parte do usuário (na instalação) para
dificultar o aparecimento da cavitação são:
1. trabalhar sempre que possível com líquidos frios (diminuindo a temperatura, diminuir a pressão de vapor)
2. tornar a linha de sucção o mais curta e reta possível, evitando excesso de acessórios, diminuindo assim a
perda de carga na sucção.
3. executar a linha de sucção em diâmetro capaz de evitar velocidade acima do recomendado (1,0 a 2,0 m/s).
4. usar redução excêntrica à entrada da bomba para evitar formação das bolsas de ar, muito comuns em
reduções concêntricas.
5. dimensionar o poço de sucção de forma a evitar que a entrada da tubulação de sucção se localize em região
de excessiva turbulência .
Todas as medidas descritas apenas dificultam o aparecimento da cavitação ou seja, apenas retardam a
destruição a ser feita pela cavitação.
A única medida capaz de assegurar o perfeito funcionamento da bomba é a sua
montagem em posição compatível com o seu projeto e as suas condições de serviço (dentro da
faixa a qual foi projetada).
6.6 NPSH (NEAT POSITIVE SUCTION HEAD)
A fim de caracterizar as condições para que ocorra boa aspiração do líquido, foi introduzida na
terminologia de instalações de bombeamento a noção de NPSH.
Esta grandeza representa a disponibilidade de energia com que o líquido penetra na boca de entrada da
bomba e que a ele permitirá atingir o bordo da pá do rotor.
O NPSH distingue-se em:
1) NPSH disponível: é a disponibilidade de energia do líquido ao entrar na bomba, a qual
depende da maneira como é projetada a instalação da bomba.
Seu valor é determinado por:
NPSH disp =
(p rs + p atm ) − pv
± Hs − ∆H (6.5)
γ
onde: prs = pressão no reservatório de sucção
patm = pressão atmosférica
pv = pressão de vapor do líquida na temperatura de bombeamento
γ = peso específico do fluído
Hs = altura geométrica de sucção (positivo = quando a bomba está acima do reservatório de sucção;
negativo = quando a bomba está abaixo do reservatório de sucção)
∆H = somatória das perdas de carga na sucção
Analisando a expressão do NPSHdisp, para obtermos valores elevados, devemos
considerar os seguintes critérios:
a) diminuir a altura geométrica de sucção negativa ou aumentar a altura geométrica de
sucção positiva.
b) minimizar as perdas de carga na sucção, tornando a linha de sucção o mais curta possível, evitando
excesso de acessórios.
c) verificar o valor da pressão atmosférica local. Para bombas instaladas acima do nível do mar, deve-se
considerar uma diminuição da pressão atmosférica de aproximadamente 0,1 bar para cada 900 m de
altitude.
d) se possível, diminuir a temperatura do fluído (diminuindo a temperatura diminui a pressão de vapor).
Através da expressão do NPSHdisp, podemos determinar a máxima altura para a colocação da bomba em
relação ao nível do reservatório (sucção negativa), para que ocorra boa aspiração (não ocorra cavitação).
2) NPSH requerido (NPSHreq) - podemos explicar NPSHreq, como sendo a carga energética líquida que a
bomba necessita para se tornar capaz de succionar o líquido.
O NPSHreq é determinado pelo fabricante da bomba, através de experimentos em bancada, e a maioria
das curvas características de uma bomba incluem a curva do NPSHreq em função da vazão.
O fim prático do NPSHreq é impor limitações às condições de sucção, de modo a manter a pressão na
entrada do rotor da bomba acima da pressão de vapor do líquido bombeado. Estas limitações são definidas pelo
fabricante mediante a curva de NPSHreq.
Desde que a energia disponível se iguale ou exceda os valores do NPSHreq, não haverá vaporização do
líquido, evitando com isso, a cavitação e suas conseqüências, deste modo, bomba deve ser selecionada,
observando a seguinte relação.
NPSH disp NPSH req (6.6)
Utiliza-se na prática uma margem entre NPSHreq e NPSHdisp mínima de 10 a 15%, porém não menor
que 0,6 m.
Existem cálculos para se obter um valor de referência para o NPSHreq, mas na prática não são
utilizados, pois somente o fabricante da bomba poderá fornecer indicações precisas do NPSHreq.
6.7 Cálculo de referência do NPSHreq para bombas
6.7.1 Conforme KSB

71. No caso de bombas KSB, modelo ETA, as curvas indicam Hs (altura de sucção) com o qual podemos
calcular o NPSHreq pela equação abaixo:
v2
NPSH req = 10 − Hs + (6.7)
2g
onde: Hs = altura de sucção obtida na curva característica (m)
vs = velocidade no flange de sucção (m/s).
6.7.2 Quando se conhece o rendimento máximo
NPSHreq = σ ⋅ H (6.8)
Segundo experiências realizadas por Stepanoff, nas proximidades do ponto de máximo rendimento,
podemos tornar para valor médio de σ:
σ = 12 × 10 −13 n4
, s (6.9)
onde: ns é a velocidade específica dada por
nQ1/ 2
ns =
H3/ 4
n é o número de rotações (rpm)
Q á a vazão (m3/s)
H é a altura manométrica (m)

72. 4a Lista de Exercícios:
1- Numa instalação de bombeamento, água se acha a 90ºC num pré-aquecedor, e é bombeada para um aquecedor
que está sob a 200Kpa. A descarga deverá ser de 20m3/h. O local da instalação se encontra a uma altitude de
520m. As perdas na aspiração correspondem a 0,8mca e no recalque 1,1 mca Deseja-se saber a que altura a
bomba deverá ficar colocada em relação ao nível da água do reservatório para que ela não cavite?
2- Uma bomba centrífuga está instalada com um desnível de sucção muito próximo do valor máximo
admissível, isto é, no limite de ocorrência de cavitação. Verifique a possibilidade de ser instalada, neste
mesmo sistema, uma outra bomba:
a) em série com a original;
b) em paralelo com a original.
3-Uma instalação de bombeamento configura-se como o esquema abaixo. A vazão atual é 22,5 m3/h. Para
atender os novos requisitos do sistema, será instalada uma bomba em paralelo com a original, do mesmo
modelo (curva característica abaixo). Determinar o novo ponto de operação do sistema, e de cada uma das
bombas (H,Q, η e N). Calcule também o novo desnível de sucção. A perda de carga no trecho de sucção da
bomba é calculado de:
Zs = 4 x 10 -3 Q2 (mca), para Q ≡ (m3/h)
Z s = 4 x1 0 -3 Q 2
6m
3
4m
H 2O h r = 9,6 mca
h v = 0,2 mca
3 0 .0 0 70
2 0 .0 0 60
)
m
(
H
. )
n
a −
(
M η
a
r
u
t
l
A 1 0 .0 0 50
0 .0 0 40
0 .0 0 1 0 .0 0 2 0 .0 0 3 0 .0 0
V a z ão (m 3 /h )

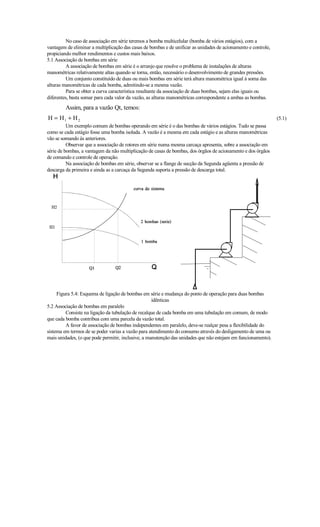
73. Capítulo 7
Ventiladores
7.1 Princípio de operação
Ventiladores são equipamentos que criam uma diferença de pressão e causam um fluxo
de gás. As pás do ventilador realizam trabalho sobre o gás, transferindo a esse energia cinética
e potencial de pressão, sendo que a proporção entre os dois tipos de energia transferida varia
conforme o tipo de ventilador.
Recordando a equação de Bernoulli:
2
p v
+ + z = cte (7.1)
ρg 2g
onde a primeira parcela representa a parcela de energia de pressão, a segunda representa a energia cinética e a
terceira a energia potencial gravitacional. Para o caso de tratarmos de gases, como sua densidade é baixa, o
termo de energia potencial gravitacional é desprezado.
Nesta forma, a equação de Bernoulli, (e portanto cada um de seus termos) é apresentada em m.c.f . ( ou
seja, metros de coluna de fluido que circula, no caso o ar).
Para transformar m.c.f. em Pa (unidade de pressão), basta multiplicar pela densidade do fluido que
circula e pela aceleração da gravidade g.
Assim, a parcela de energia cinética, chamada Pressão dinâmica é dada pelo termo:
2
v
pdin = ρf x (7.2)
2
onde: pdin é a pressão dinâmica [Pa];
ρf é a densidade do fluido [kg/m3]
É comum se fornecer a pressão dinâmica como a altura de coluna de líquido manométrico utilizado na
sua medição ( normalmente água), assim, lembrando que a densidade da água é de 1000 kg/m3, e a aceleração
da gravidade é 9,81 m/s2, tendo-se o valor da pressão dinâmica em mm de coluna d'água, basta multiplicá-la por
9,81 para obter-se o valor em Pa.
Outro termo também utilizado para exprimir esta parcela de energia cinética é Altura dinâmica (Hd),
sendo então expressa em metros de coluna do fluido que está escoando (normalmente ar para ventiladores).
A parcela de energia potencial de pressão é chamada de pressão estática. Utiliza-se o termo Altura
estática (He) quando esta parcela de energia é dada em termos de altura coluna do fluido escoando. Como
também é medida em coluna de água, seu valor é dado em mm de coluna d'água, entretanto para passá-la para
altura de coluna de ar, deve-se multiplicar pela densidade da água e dividir
pela densidade do ar.
A soma das pressões dinâmica e estática é a pressão total do fluxo. A diferença entre a pressão total na
saída e na entrada do ventilador é a energia fornecida ao fluxo. Quando esta é apresentada em termos de altura
de coluna de fluido circulando, é chamada altura útil de elevação (Hu).
Assim, a potência total recebida pelo fluxo de fluido é dada por:
w u = ρf .g.Q. H u
(7.3)
onde wu é a potência transferida ao fluido [W]
ρf é a densidade do fluido [kg/m3]
g é a aceleração da gravidade [m/s2]
Hué a altura útil de elevação [m]
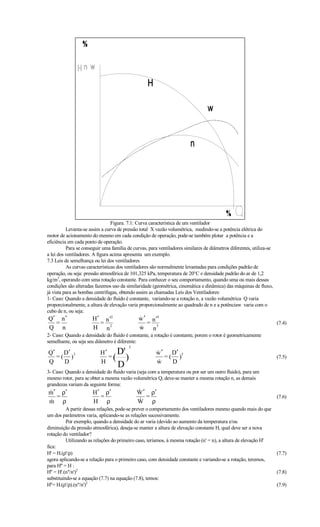
7.2 Levantamento das curvas características de um ventilador:
Existem normas para teste de ventiladores, entretanto os procedimentos são relativamente simples: um
tubo de Pitot é colocado perpendicular ao fluxo de saída do ventilador e são tomadas medidas de pressão estática
e dinâmica a uma rotação constante, variando-se a vazão através do estrangulamento na saída do mesmo, desde
completamente fechada até a abertura total.

74. Figura. 7.1: Curva característica de um ventilador
Levanta-se assim a curva de pressão total X vazão volumétrica, medindo-se a potência elétrica do
motor de acionamento do mesmo em cada condição de operação, pode-se também plotar a potência e a
eficiência em cada ponto de operação.
Para se conseguir uma família de curvas, para ventiladores similares de diâmetros diferentes, utiliza-se
a lei dos ventiladores. A figura acima apresenta um exemplo.
7.3 Leis de semelhança ou lei dos ventiladores
As curvas características dos ventiladores são normalmente levantadas para condições padrão de
operação, ou seja: pressão atmosférica de 101,325 kPa, temperatura de 20°C e densidade padrão do ar de 1,2
kg/m3, operando com uma rotação constante. Para conhecer o seu comportamento, quando uma ou mais dessas
condições são alteradas fazemos uso da similaridade (geométrica, cinemática e dinâmica) das máquinas de fluxo,
já vista para as bombas centrífugas, obtendo assim as chamadas Leis dos Ventiladores:
1- Caso: Quando a densidade do fluido é constante, variando-se a rotação n, a vazão volumétrica Q varia
proporcionalmente, a altura de elevação varia proporcionalmente ao quadrado de n e a potênciaw varia com o
cubo de n, ou seja:
Q′ n ′ H ′ n ′2 w ′ n ′3
= = = (7.4)
Q n H n2 w n3
2- Caso: Quando a densidade do fluido é constante, a rotação é constante, porem o rotor é geometricamente
semelhante, ou seja seu diâmetro é diferente:
2
Q′ D ′ 3 H′
=(
D' w ′ D′ 5
Q
=( )
D H
)
w
=( )
D
(7.5)
D
3- Caso: Quando a densidade do fluido varia (seja com a temperatura ou por ser um outro fluido), para um
mesmo rotor, para se obter a mesma vazão volumétrica Q, deve-se manter a mesma rotação n, as demais
grandezas variam da seguinte forma:
m ′ ρ′
H ′ ρ′ W ′ ρ′
= = = (7.6)
m ρ
H ρ W ρ
A partir dessas relações, pode-se prever o comportamento dos ventiladores mesmo quando mais do que
um dos parâmetros varia, aplicando-se as relações sucessivamente.
Por exemplo, quando a densidade do ar varia (devido ao aumento da temperatura e/ou
diminuição da pressão atmosférica), deseja-se manter a altura de elevação constante H, qual deve ser a nova
rotação do ventilador?
Utilizando as relações do primeiro caso, teríamos, à mesma rotação (n' = n), a altura de elevação H'
fica:
H' = H.(ρ'/ρ) (7.7)
agora aplicando-se a relação para o primeiro caso, com densidade constante e variando-se a rotação, teremos,
para H'' = H :
H'' = H'.(n''/n')2 (7.8)
substituindo-se a equação (7.7) na equação (7.8), temos:
H''= H.(ρ'/ρ).(n''/n')2 (7.9)

75. como H'' = H e n = n', temos:
n = n × ρ / ρ (7.10)
7.4 Tipos de ventiladores e suas principais características:
Os ventiladores são geralmente classificados como centrífugos ou axiais, de acordo com a direção do
fluxo de ar através das pás. A figura abaixo mostra a configuração geral de um ventilador centrífugo e um axial
com seus principais componentes.
Um quadro geral comparativo das principais características dos ventiladores mais comumente
utilizados é apresentado a seguir: (tabela 7.1) e (7.2)
7.5 Curva característica do sistema:
Quase todas as instalações de ventilação, exaustão ou distribuição de ar utilizam um sistema de dutos,
filtros, registros, acessórios em geral, constituindo assim o que se denomina sistema de dutos. Esse sistema
oferece uma determinada resistência ao escoamento devido ao atrito com as paredes o que provoca uma perda de
carga. Assim, para promover o escoamento do fluido através do sistema, é necessário fornecer a energia que será
dissipada por esse sistema, sendo que o ventilador é a máquina utilizada para este fim.
Como já vimos, a energia fornecida pelo ventilador ao fluido é a chamada altura útil de elevação (Hu),
que é a soma da altura dinâmica (Hd) e da altura estática (He). Graças a essa energia, o fluido irá vencer as
resistências do sistema de dutos e sairá, ao final deste com uma energia cinética residual que se dissipará no
ambiente, e que portanto é computada como perda de carga, ou seja, para que o ventilador forneça a quantidade
de energia suficiente para vencer as resistências do sistema de dutos temos:

77. Hu = ∆P (7.11)
onde ∆P é a perda de carga total do sistema de dutos, incluindo a perda de energia cinética residual da saída.
A curva representativa das perdas de carga do sistema em função da vazão denomina-se curva
característica do sistema. Para sabermos o ponto de operação do sistema de dutos acoplado a um determinado
ventilador, basta plotarmos a curva característica do sistema e do ventilador juntas e a intersecção entre as duas
nos dará o ponto de operação.
A curva característica do sistema é função do regime de escoamento que está ocorrendo, como já foi
visto para os sistemas de bombeamento de líquidos, quando o regime de escoamento é laminar, as perdas de
carga são proporcionais à velocidade, e portanto à vazão, assim, a curva característica é uma reta, já que a perda
de carga varia linearmente com a vazão.
Figura 7.2: Curvas características de um sistema em regime laminar (esquerda) e turbulento (direita)com válvula
bem fechada(A), mais aberta (B) e muito mais aberta (C)
Para a maioria dos escoamentos, entretanto, o regime de escoamento é turbulento ( o
número de Reynolds é maior que 2.400) e nesse caso, as perdas de carga são proporcionais ao
quadrado da vazão, gerando uma curva característica em forma de parábola.
Controle de vazão:
Uma das formas possíveis para se controlar a vazão em um sistema de dutos é variando-se a sua perda
de carga total através de uma válvula. Fechando-se a válvula gradativamente, estaremos modificando a curva
característica do sistema, tornando-a mais íngreme. Abrindo-se a válvula a curva se torna mais suave,
modificando assim o ponto de operação (cruzamento entre a curva do sistema e do ventilador), conforme pode
ser visto na figura anterior.
7.6 Operação de ventiladores em série e em paralelo.
Assim como já foi visto para as bombas centrífugas, também com ventiladores podemos recorrer a
associações de ventiladores em série ou em paralelo.
7.6.1 Associação em Série:
Quando se necessita de uma pressão (altura útil) relativamente elevada, pode-se utilizar a associação de
dois ou mais ventiladores em série, basta montar um dos ventiladores insuflando ar na aspiração do outro. Neste
caso, temos que a vazão volumétrica que passa pelos dois ventiladores é igual e a altura útil é a somatória das
alturas obtidas por cada um deles. Assim, para se obter a curva resultante da associação de dois ventiladores em
série, basta para cada valor de vazão dado, somar as alturas úteis dos dois ventiladores.
A figura (7.3) mostra que a curva do sistema interceptará a curva resultante em um ponto que não é
correspondente ao dobro da altura útil obtida com um único ventilador, mas sim um pouco menos, entretanto, há
um aumento da vazão resultante.
Figura 7.3: Operação de dois ventiladores idênticos em série Figura 7.4: Associação em paralelo de dois
ventiladores iguais, ligados a um sistema de
dutos
7.6.2 Associação em Paralelo:

78. Quando a faixa de variação de vazão para uma determinada aplicação é muito grande, para se evitar
que um ventilador opere em pontos de baixa eficiência, é comum recorrer-se à associação de ventiladores em
paralelo.
Para se obter a curva resultante da associação de dois ventiladores em paralelo, basta, para cada valor
da altura útil da curva de cada ventilador, somar-se as vazões obtidas em cada um deles.
Também neste caso, a curva do sistema interceptará a curva resultante em um ponto que terá uma
altura útil maior que a obtida com um só ventilador e a vazão obtida será maior, mas não o dobro da vazão
original, conforme se vê na figura abaixo.
Para os ventiladores que apresentam uma curva característica com diminuição da altura útil a esquerda
do pico ( como os axiais e centrífugos com pás para a frente, por exemplo), deve-se escolher um ponto de
operação sempre à direita do pico de pressão da curva resultante, caso contrário teremos a operação instável dos
ventiladores, com mais de um ponto de operação possível para cada ventilador atendendo aos requisitos de vazão
total e altura útil do sistema.
A figura (7.5) procura mostrar essa situação para dois ventiladores centrífugos de pás para frente
Figura 7.5: Dois ventiladores centrífugos com pás curvadas para frente iguais operando em paralelo.
Nesta figura observamos as curvas de altura útil de um único ventilador e de dois ventiladores idênticos
em paralelo. A figura característica em forma de ∞ é o resultado de todas as combinações possíveis de vazão
de cada ventilador para a mesma altura útil. Assim, para a operação estável dos dois ventiladores em paralelo, a
curva do sistema deve interceptar a curva resultante da associação a direita do ponto de máxima altura útil, como
no caso da curva do sistema menos íngreme (B). Caso a curva do sistema seja a curva (A), podemos ver que
temos duas intersecções com a curva resultante da associação, e portanto, dois pontos possíveis de operação. Na
intersecção superior, teríamos os dois ventiladores com a mesma vazão (metade da total) e uma altura útil mais
alta. Na intersecção inferior, teríamos um dos ventiladores operando em um ponto a esquerda do pico de altura
útil, e portanto com uma vazão mais baixa e o outro operando em um ponto a direita do pico de altura útil e com
vazão mais elevada. Este desbalanceamento de vazões entre os dois ventiladores diminui a eficiência global do
sistema e pode danificar os ventiladores. Este modo de operação é instável, sendo que o sistema pode ficar
variando entre um ponto de operação e outro.